1、递归算法
图 1 展示了函数递归调用的底层实现过程:
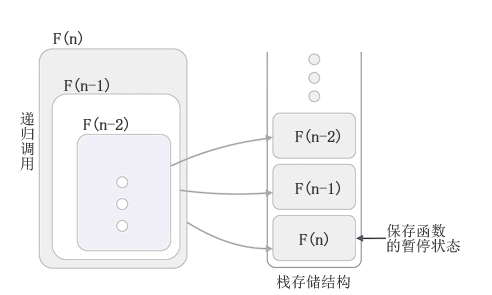
图 1 递归的底层实现
如图 1 所示,F(n) 调用了 F(n-1),因此 F(n) 会暂停执行,将执行代码的权力移交给 F(n-1),F(n) 的暂停状态也会入栈保存;同样的道理,F(n-1) 中调用了 F(n-2),所以 F(n-1) 暂停执行,暂停状态入栈保存,执行代码的权力移交给 F(n-2)……直至递归停止,执行代码的权力会移交给栈中最顶部的函数,该函数的暂停状态信息会从栈中取出并恢复,该函数继续执行,执行完成后再将执行权力移交给栈顶的函数。直至 F(n) 出栈并执行完成,整个递归过程才算完成。
2、斐波那契数列
公元 1202 年,意大利数学家莱昂纳多·斐波那契提出了具备以下特征的数列:
- 前两个数的值分别为 0 、1 或者 1、1;
- 从第 3 个数字开始,它的值是前两个数字的和;
为了纪念他,人们将满足以上两个特征的数列称为斐波那契数列。
如下就是一个斐波那契数列:
1 1 2 3 5 8 13 21 34……
下面的动画展示了斐波那契数列的生成过程:

代码实现:
public class Demo {// index 表示求数列中第 index 个位置上的数的值public static int fibonacci(int index) {// 设置结束递归的限制条件if (index == 1 || index == 2) {return 1;}// F(index) = F(index-1) + F(index-2)return fibonacci(index - 1) + fibonacci(index - 2);}public static void main(String[] args) {// 输出前 10 个数for (int i = 1; i <= 10; i++) {System.out.print(fibonacci(i) + " ");}}}
程序结果:
3、分治算法
实际场景中,我们之所以觉得有些问题很难解决,主要原因是该问题涉及到大量的数据,如果只需要处理少量的数据,问题会变得非常容易解决。
举一个简单的例子,设计一个排序算法实现对 1000 个整数进行排序。对于很多刚刚接触算法的初学者来说,直接实现对 1000 个整数进行排序是非常困难的。而同样的问题,如果转换成对 2 个整数进行排序,解决起来就很容易。
分治算法中,“分治”即“分而治之”的意思。分治算法解决问题的思路是:先将整个问题拆分成多个相互独立且数据量更少的小问题,通过逐一解决这些简单的小问题,最终找到解决整个问题的方案。
所谓问题间相互独立,简单理解就是每个问题都可以单独处理,不存在“谁先处理,谁后处理”的次序问题。
分治算法解决问题的过程如图 1 所示: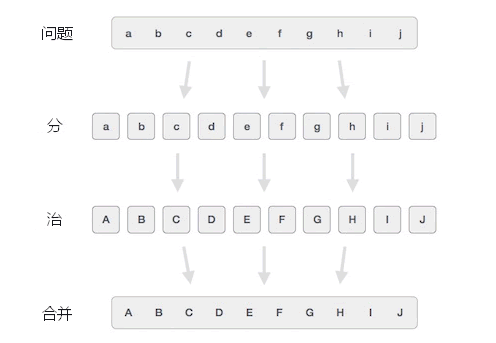
图 1 分治算法解决问题的过程
如图 1 所示,分治算法解决问题的过程需要经历 3 个阶段,分别是:
- 分:将整个问题划分成多个相对独立、涉及数据量更少的小问题,有些小问题还可以划分成很多更小的问题,直至每个问题都不可再分;
- 治:逐个解决所有的小问题;
- 合并:将所有小问题的解决方案合并到一起,找到解决整个问题的方案。
分治算法的利弊
使用分治算法解决的问题都具备这样的特征,当需要处理的数据量很少时,问题很容易就能解决,随着数据量增多,问题的解决难度也随之增大。分治算法通过将问题“分而治之”,每个小问题只需要处理少量的数据,每个小问题都很容易解决,最终就可以解决整个问题。
分治算法中,“分而治之”的小问题之间是相互独立的,处理次序不分先后,因此可以采用“并行”的方式让计算机同时处理多个小问题,提高问题的解决效率。
分治算法的弊端也很明显,该算法经常和递归算法搭配使用,整个解决问题的过程会耗费较多的时间和内存空间,严重时还可能导致程序运行崩溃。
分治算法的应用场景
分治算法解决的经典问题有很多,包括汉诺塔问题、寻找数列中最大值和最小值的问题等等。
分治算法还和其它算法搭配使用,比如二分查找算法、归并排序算法、快速排序算法等,后续章节会给大家一一进行讲解。
4、贪心算法
《算法是什么》一节讲到,算法规定了解决问题的具体步骤,即先做什么、再做什么、最后做什么。贪心算法是所有算法中最简单,最易实现的算法,该算法之所以“贪心”,是因为算法中的每一步都追求最优的解决方案。
举个例子,假设有 1、2、5、10 这 4 种面值的纸币,要求在不限制各种纸币使用数量的情况下,用尽可能少的纸币拼凑出的总面值为 18。贪心算法的解决方案如下:
- 率先选择一张面值为 10 的纸币,可以最大程度上减少需要拼凑的数额(剩余 8);
- 选择一张面值为 5 的纸币,需要拼凑的数额降为 3;
- 选择一张面值为 2 的纸币,需要拼凑的数额降为 1;
- 选择一张面值为 1 的纸币,完成拼凑。
可以看到,每一步都力求最大限度地解决问题,每一步都选择的是当前最优的解决方案,这种解决问题的算法就是贪心算法。
注意,虽然贪心算法每一步都是最优的解决方案,但整个算法并不一定是最优的。仍以选纸币为例,假设有 1、7、10 这 3 种面值的纸币,每种纸币使用的数量不限,要求用尽可能少的纸币拼凑出的总面值为 15,贪心算法的解决方案为:
- 选择一张面值为 10 的纸币,需要拼凑的数额降为 5;
- 选择一张面值为 1 的纸币,需要拼凑的数额降为 4;
- 选择一张面值为 1 的纸币,需要拼凑的数额降为 3;
- 选择一张面值为 1 的纸币,需要拼凑的数额降为 2;
- 选择一张面值为 1 的纸币,需要拼凑的数额降为 1;
- 选择一张面值为 1 的纸币,完成拼凑。
最终贪心算法给出的解决方案是 10+1+1+1+1+1 共 6 张纸币,但是通过思考,最优的解决方案应该是只需要用 3 张纸币(7+7+1)。
总的来讲,贪心算法注重的是每一步选择最优的解决方案(又称“局部最优解”),并不关心整个解决方案是否最优。
贪心算法的实际应用
部分背包问题是使用贪心算法解决的典型案例之一,此外它还经常和其它算法混合使用,例如克鲁斯卡尔算法、迪杰斯特拉算法等,我们会在后续章节一一进行讲解。
5、动态规划算法
动态规划算法解决问题的过程和分治算法类似,也是先将问题拆分成多个简单的小问题,通过逐一解决这些小问题找到整个问题的答案。不同之处在于,分治算法拆分出的小问题之间是相互独立的,而动态规划算法拆分出的小问题之间相互关联,例如要想解决问题 A,必须先解决问题 B 和 C。
《贪心算法》一节中,给大家举过一个例子,假设有 1、7、10 这 3 种面值的纸币,每种纸币使用的数量不限,要求用尽可能少的纸币拼凑出的总面值为 15。贪心算法最终给出的拼凑方案是需要 10+1+1+1+1+1 共 6 张纸币,而如果用动态规划算法解决这个问题,可以得出最优的拼凑方案,即只需要 1+7+7 共 3 张纸币。
动态规划算法的解题思路是:用 f(n) 表示凑齐面值 n 所需纸币的最少数量,面值 15 的拼凑方案有 3 种,分别是:
- f(15) = f(14) +1:挑选一张面值为 1 的纸币,f(14) 表示拼凑出面值 14 所需要的最少的纸币数量;
- f(15) = f(8) + 1:挑选一张面值为 7 的纸币,f(8) 表示拼凑出面值 8 所需要的最少的纸币数量;
- f(15) = f(5) + 1:选择一张面值为10 的纸币,f(5) 表示拼凑出面值 5 所需要的最少的纸币数量。
也就是说,f(14)+1、f(8)+1 和 f(5)+1 三者中的最小值就是最优的拼凑方案。采用同样的方法,继续求 f(14)、f(8)、f(5) 的值:
感兴趣的读者还可以继续拆分 f(4)、f(7)、f(13) 等。经过不断地拆分,f(15) 最终会和 f(0)、f(1)、f(2) 等产生关联,而 f(0)、f(1)、f(2) 的值是很容易计算的。在得知 f(0)、f(1)、f(2) 等简单问题的结果后,就可以轻松推算出 f(3)~f(14) 的值,最终可以推算出 f(15) 的值。
对于每种纸币来说,是否使用它可能会影响 f(n) 的值。接下来,我们就一一分析三种纸币对 f(0)~f(15) 的影响:
1) 在不能使用任何纸币的情况下,f(1)~f(15) 没有对应的值,我们用 ∞ 表示它们的值:
2) 使用面值为 1 的纸币,可以对表 1 中各个拼凑方案对应的值进行优化,如表 2 所示:
3) 使用面值为 7 的纸币,可以对表 2 中各个拼凑方案做进一步优化:
f(0)~f(6) 中无法使用面值为 7 的纸币,而 f(7)~f(15) 可以选择面值为 7 的纸币,它们各自产生了更优的解决方案:f(7)=f(0)+1,f(8)=f(1)+1,…,f(15)=f(8)+1。以 f(7) 为例,除了使用先前的 f(6)+1 方案,还可以选择 f(0)+1 方案,显然后者更优,只需要一张纸币。
4) 使用面值为 10 的纸币,继续对表 3 进行优化:
对比表 2 不难发现,面值为 10 的纸币仅对 f(10)~f(13) 起到了优化的作用,而对于 f(14) 和 f(15) 来说,选择面值为 10 的纸币,并没有先前的解决方案好。最终,f(15) 的最优拼凑方案是只需要 3 张纸币(7+7+1)。
以上我们解决问题所用的方法就是动态规划算法。总的来说,动态规划算法就是不断地拆分问题,拆分出的这些小问题之间相关关联,通过解决一些简单的问题,复杂的问题也能迎刃而解。
《贪心算法》一节提到,背包问题的种类有很多,其中部分背包问题可以用贪心算法解决,而 0-1 背包问题则可以用动态规划算法解决。
此外,弗洛伊德算法在解决最短路径问题的过程中,也用到了“动态规划”的思想,后续章节会给大家做详细地讲解。
- f(5) = f(4) + 1;
- f(8) = f(7) + 1 = f(1) +1;
- f(14) = f(13)+1 = f(7) + 1 = f(4) +1。 | 选择的纸币 | f(n) 的所有情况 | | | | | | | | | | | | | | | | | —- | —- | —- | —- | —- | —- | —- | —- | —- | —- | —- | —- | —- | —- | —- | —- | —- | | | f(0) | f(1) | f(2) | f(3) | f(4) | f(5) | f(6) | f(7) | f(8) | f(9) | f(10) | f(11) | f(12) | f(13) | f(14) | f(15) | | 不选择任何纸币 | 0 | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ | ∞ |
| 选择的纸币 | f(n) 的所有情况 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(0) | f(1) | f(2) | f(3) | f(4) | f(5) | f(6) | f(7) | f(8) | f(9) | f(10) | f(11) | f(12) | f(13) | f(14) | f(15) | |
| 选择面值为 1 的纸币 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 | 11 | 12 | 13 | 14 | 15 |
f(1)~f(14) 对应的值都可以优化,计算方式是:f(1)=f(0)+1,f(2)=f(1)+1,f(3)=f(2)+1… f(15)=f(14)+1 。
| 选择的纸币 | f(n) 的所有情况 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(0) | f(1) | f(2) | f(3) | f(4) | f(5) | f(6) | f(7) | f(8) | f(9) | f(10) | f(11) | f(12) | f(13) | f(14) | f(15) | |
| 选择面值为 7 的纸币 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 2 | 3 |
| 选择的纸币 | f(n) 的所有情况 | |||||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| f(0) | f(1) | f(2) | f(3) | f(4) | f(5) | f(6) | f(7) | f(8) | f(9) | f(10) | f(11) | f(12) | f(13) | f(14) | f(15) | |
| 选择面值为 10 的纸币 | 0 | 1 | 2 | 3 | 4 | 5 | 6 | 1 | 2 | 3 | 1 | 2 | 3 | 4 | 2 | 3 |
动态规划算法的实际应用
《贪心算法》一节提到,背包问题的种类有很多,其中部分背包问题可以用贪心算法解决,而 0-1 背包问题则可以用动态规划算法解决。
此外,弗洛伊德算法在解决最短路径问题的过程中,也用到了“动态规划”的思想,后续章节会给大家做详细地讲解。
6、回溯算法
图 1 中找到从 A 到 K 的行走路线,一些读者会想到用穷举算法(简称穷举法),即简单粗暴地将从 A 出发的所有路线罗列出来,然后逐一筛选,找到正确的路线。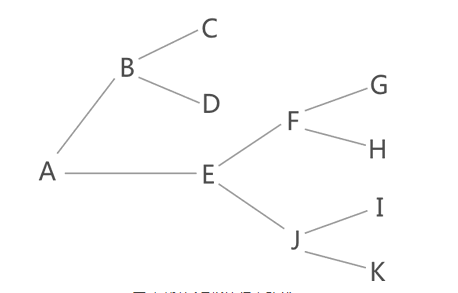
图 1 找从A到K的行走路线
图 1 中,从 A 出发的路线有以下几条:
A-B-C
A-B-D
A-E-F-G
A-E-F-H
A-E-J-I
A-E-J-K
穷举法会一一筛选这些路线,最终找到 A-E-J-K 。
本节要讲的回溯算法和穷举法很像,它也会把所有可能的方案都查看一遍,从中找到正确答案。不同之处在于,回溯算法查看每种方案时,一旦判定其不是正确答案,会立即以“回溯”的方式试探其它方案。
所谓“回溯”,其实就是回退、倒退的意思。仍以图 1 为例,回溯算法查找从 A 到 K 路线的过程是:
- 从 A 出发,先选择 A-B 路线;继续从 B 出发,先选择 B-C 路线;到达 C 点后发现无路可选,表明当前路线无法达到 K 点,该算法会立刻回退到上一个节点,也就是 B 点;
- 从 B 点出发,选择 B-D 路线,达到 D 点后发现无法到达 K 点,该算法再回退到 B 点;
- 从 B 点出发已经没有新的线路可以选择,该算法再次回退到 A 点,选择新的 A-E 路线;
- 继续以同样的方式测试 A-E-F-G、A-E-F-H、A-E-J-I 这 3 条线路后,最终找到 A-E-J-K 路线。
回溯算法采用“回溯”(回退)的方式对所有的可行方案做出判断,并最终找到正确方案。和穷举法相比,回溯算法的查找效率往往更高,因为在已经断定当前方案不可行的情况下,回溯算法能够“悬崖勒马”,及时转向去判断其它的可行方案。
回溯算法的应用场景
回溯算法经常以递归的方式实现,用来解决以下 3 类问题:
- 决策问题:从众多选择中找到一个可行的解决方案;
- 优化问题:从众多选择中找到一个最佳的解决方案;
- 枚举问题:找出能解决问题的所有方案。
用回溯算法解决的经典问题有 N皇后问题、迷宫问题等,我们会在后续章节给大家做详细地讲解。
7、冒泡排序算法
实现思路是:
- 从待排序序列中找出一个最大值或最小值,遍历待排序序列,过程中不断地比较相邻两个元素的值,如果后者比前者的值小就交换它们的位置。遍历完成后,最后一个元素就是当前待排序序列中最大的。
- 这样的操作执行 n-1 次,最终就可以得到一个有序序列。
举个例子,对 {14, 33, 27, 35, 10} 序列进行升序排序(由小到大排序),冒泡排序算法的实现过程是:
- 从 {14, 33, 27, 35, 10} 中找到最大值 35;
- 从 {14,33,27,10} 中找到最大值 33;
- 从 {14, 27, 10} 中找到最大值 27;
- 从 {14, 10} 中找到最大值 14;
由此,我们就得到了一个有序序列 {10, 14, 27, 33, 35}。
例如,从 {14, 33, 27, 35, 10} 中找到最大值 35 的过程如下:
1) 比较 14 和 33 的大小,显然后者更大,不需要交换它们的位置,序列不发生改变。
2) 比较 33 和 27 的大小,前者大于后者,交换它们的位置,新的序列如下图所示。
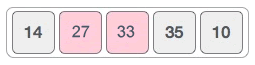
3) 比较 33 和 35 的大小,后者更大,不需要交换它们的位置,序列不发生改变。
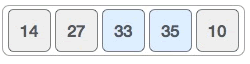
4) 比较 35 和 10 的大小,前者大于后者,交换它们的位置,新的序列如下图所示。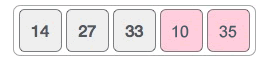
可以看到,序列中值最大的元素 35 被移动到了序列的末尾。整个查找最大值的过程中,最大的元素就像水里的气泡一样,一点一点地“冒”了出来,这也是将该算法命名为冒泡排序算法的原因。
采用同样的方法,我们可以很轻松地从 {14, 27, 33, 10} 中找到最大值 33。找到 33 后的新序列为: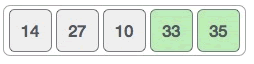
从 {14, 27, 10} 中找到最大值 27 后,新的序列如下图所示: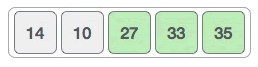
从 {14, 10} 中找到最大值 14 后,新的序列如下图所示: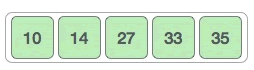
所有比 10 大的数都被一一找到,所以 10 必然是最小的数,这也是为什么“对 n 个数据进行排序,找最大值的过程只重复 n-1 次”的原因。
代码实现:
public class Demo {public static void Bubble_sort(int[] list) {int length = list.length;// length 个元素,遍历 length-1 次for (int i = 0; i < length-1; i++) {// 从第 1 个元素开始遍历,遍历至 length-1-ifor (int j = 0; j < length - 1 - i; j++) {// 比较 list[j] 和 list[j++] 的大小if (list[j] > list[j + 1]) {// 交换 2 个元素的位置int temp = list[j];list[j] = list[j + 1];list[j + 1] = temp;}}}}public static void main(String[] args) {int[] list = { 14, 33, 27, 35, 10 };Bubble_sort(list);// 输出已排好序的序列for (int i = 0; i < list.length; i++) {System.out.print(list[i] + " ");}}}
程序结果:
8、插入排序算法
插入排序算法可以对指定序列完成升序(从小到大)或者降序(从大到小)排序,对应的时间复杂度为O(n2)。
插入排序算法的实现思路是:初始状态下,将待排序序列中的第一个元素看作是有序的子序列。从第二个元素开始,在不破坏子序列有序的前提下,将后续的每个元素插入到子序列中的适当位置。
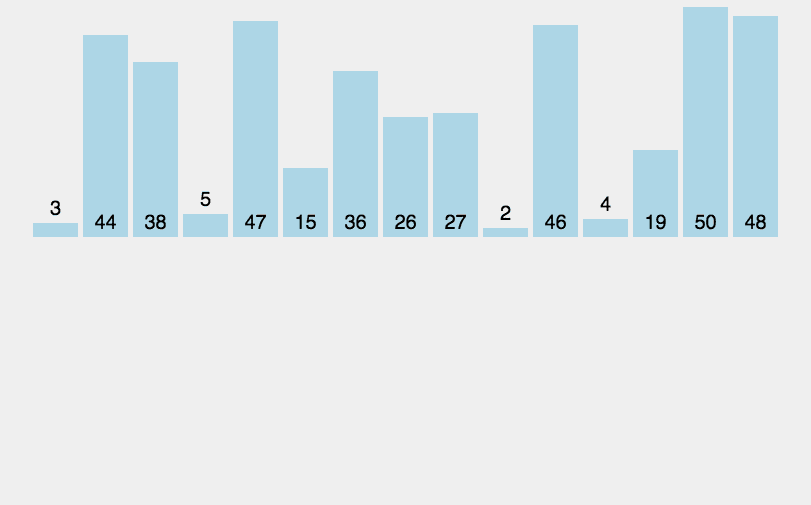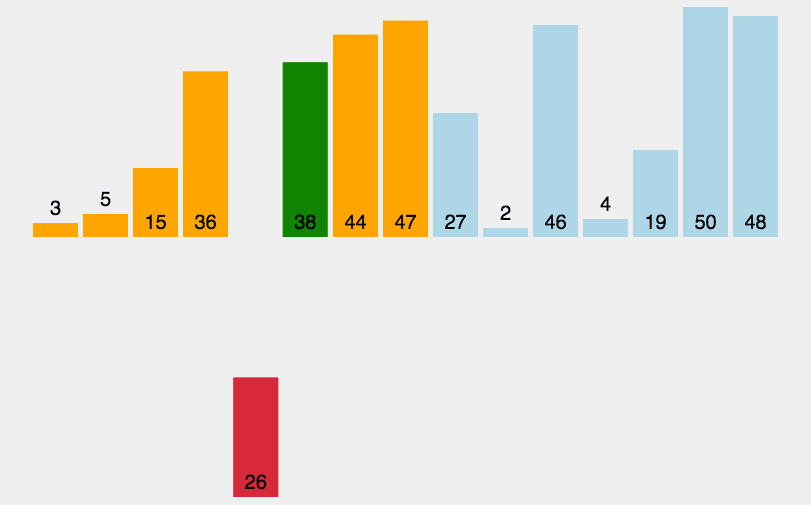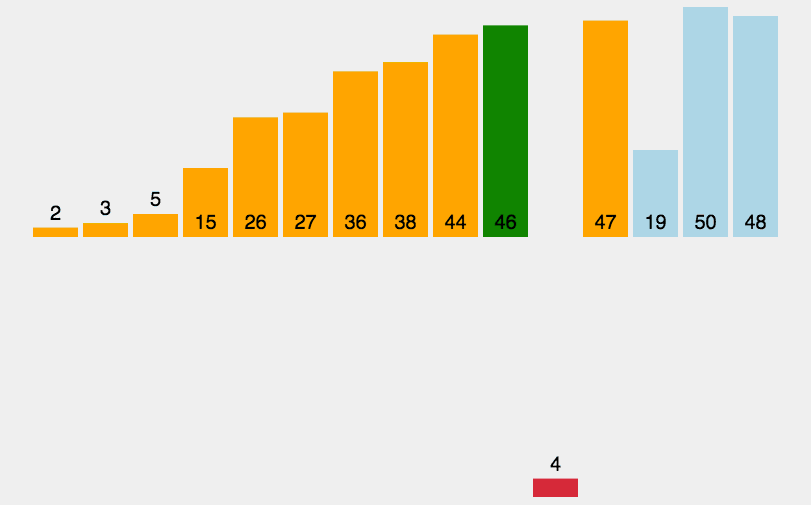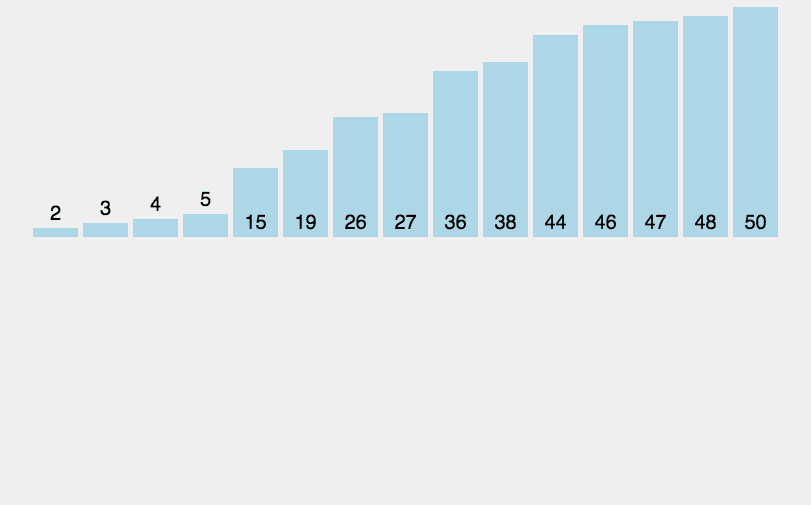
图 1 插入排序算法
举个简单的例子,用插入排序算法对 {14, 33, 27, 10, 35, 19, 42, 44} 实现升序排序的过程如下:
1) 将第一个元素 14 看作是一个有序的子序列 {14},将剩余元素逐个插入到此序列的适当位置:
2) 将 33 插入到 {14} 中,由于 33 > 14,所以 33 应该插入到 14 的后面,新的有序序列变为 {14, 33};
3) 将 27 插入到 {14, 33} 中,由于 27 < 33 同时 27 > 14,所以 27 应该插入到 14 和 33 的中间,新的有序序列变为 {14, 27, 33};
4) 将 10 插入到 {14, 27, 33} 中,经过依次和 33、27、14 比较,最终断定 10 应该插入到 14 之前,新的有序序列变为 {10, 14, 27, 33};
5) 将 35 插入到 {10, 14, 27, 33} 中,由于 35 > 33,所以 35 应该插入到 33 之后,新的有序序列变为 {10, 14, 27, 33, 35};
6) 将 19 插入到 {10, 14, 27, 33, 35} 中,经过依次和 35、33、27、14 比较,最终断定 19 应该插入到 14 和 27 之间,新的有序序列变为 {10, 14, 19, 27, 33, 35};
7) 将 42 插入到 {10, 14, 19, 27, 33, 35} 中,由于 42 > 35,所以 42 应插入到 35 之后,新的有序序列变为 {10, 14, 19, 27, 33, 35, 42};
8) 将 44 插入到 {10, 14, 19, 27, 33, 35, 42} 中,由于 44 > 42,所以 44 应插入到 42 之后,新的有序序列变为 {10, 14, 19, 27, 33, 35, 42, 44}。
经过将各个待排序的元素插入到有序序列的适当位置,最终得到的就是一个包含所有元素的有序序列。
代码实现:
public class Demo {public static void insertion_sort(int[] list) {int length = list.length;// 从第 2 个元素(下标为 1)开始遍历for (int i = 1; i < length; i++) {// 记录要插入的目标元素int insert_elem = list[i];// 记录目标元素所在的位置,从此位置向前开始遍历int position = i;// 从 position 向前遍历,找到目标元素的插入位置while (position > 0 && list[position - 1] > insert_elem) {// position 处的元素向后移动一个位置list[position] = list[position - 1];position--;}// 将目标元素插入到指定的位置if (position != i) {list[position] = insert_elem;}}}public static void main(String[] args) {int[] list = { 10, 14, 19, 27, 33, 35, 42, 44 };insertion_sort(list);// 输出已排好序的序列for (int i = 0; i < list.length; i++) {System.out.print(list[i] + " ");}}}
程序结果:
9、选择排序法
对数据量较少的序列实现升序或降序排序,可以考虑使用选择排序算法,它对应的时间复杂度为O(n2)。
排序排序算法对含有 n 个元素的序列实现排序的思路是:每次从待排序序列中找出最大值或最小值,查找过程重复 n-1 次。对于每次找到的最大值或最小值,通过交换元素位置的方式将它们放置到适当的位置,最终使整个序列变成有序序列。
举个例子,我们使用选择排序算法对 {14, 33, 27, 10, 35, 19, 42, 44} 完成升序排序,需要经历以下几个步骤:
1) 遍历整个待排序序列,从中找到最小值 10 并与第一个元素 14 交换位置:
2) 待排序序列变成 {33, 27, 14, 35, 19, 42, 44},从中找到最小值 14 并与 33 交换位置:
3) 待排序序列变成 {27, 33, 35, 19, 42, 44},从中找到最小值 19 并与 27 交换位置:
4) 待排序序列变成 {33, 35, 27, 42, 44},从中找到最小值 27 并与 33 交换位置:
5) 待排序序列变成 {35, 33, 42, 44},从中找到最小值 33 并与 35 交换位置:
6) 待排序序列变成 {35, 42, 44},从中找到最小值 35,它的位置无需变动:
7) 待排序序列变成 {42, 44},从中找到最小值 42,它的位置无需变动:
对于包含 n 个元素的待排序序列,选择排序算法中只需要找出 n-1 个“最小值”,最后剩下的元素的值必然最大。由此,我们就得到了一个升序序列 {10, 14, 19, 27, 33, 35, 42, 44}。
选择排序算法可以看作是冒泡排序算法的“改良版”。和后者相比,选择排序算法大大减少了交换数据存储位置的操作。
代码实现:
public class Demo {// list[N] 为存储待排序序列的数组public static void selection_sort(int[] list) {int length = list.length;int i, j;// 从第 1 个元素开始遍历,直至倒数第 2 个元素for (i = 0; i < length - 1; i++) {int min = i; // 事先假设最小值为第 i 个元素// 从第 i+1 个元素开始遍历,查找真正的最小值for (j = i + 1; j < length; j++) {if (list[j] < list[min]) {min = j;}}// 如果最小值所在位置不为 i,交换最小值和第 i 个元素的位置if (min != j) {int temp = list[min];list[min] = list[i];list[i] = temp;}}}public static void main(String[] args) {int[] list = { 14, 33, 27, 10, 35, 19, 42, 44 };selection_sort(list);// 输出已排好序的序列for (int i = 0; i < list.length; i++) {System.out.print(list[i] + " ");}}}
程序结果:
10、希尔排序算法
实现思路:
- 将待排序序列划分成多个子序列,使用普通的插入排序算法对每个子序列进行排序;
- 按照不同的划分标准,重复执行第一步;
- 使用普通的插入排序算法对整个序列进行排序。
对 {35, 33, 42, 10, 14, 19, 27, 44} 做升序排序,具体的实现流程是:
1) 间隔 4 个元素,将整个序列划分为 4 个子序列: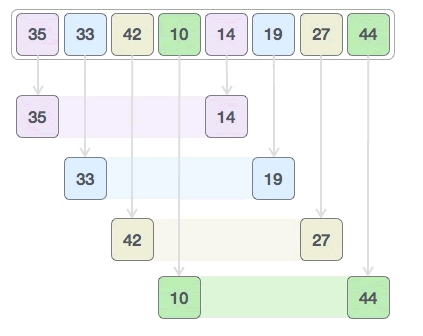
采用插入排序算法分别对 {35, 14}、{33, 19}、{42, 27}、{10, 44} 进行排序,最终生成的新序列为:
2) 间隔 2 个元素,再次划分整个序列: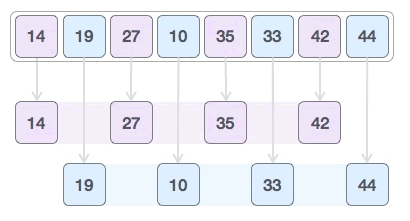
采用插入排序算法分别对 {14, 27, 35, 42} 和 {19, 10, 33, 44} 进行排序:
3) 采用插入排序算法对整个序列进行一次排序,过程如下: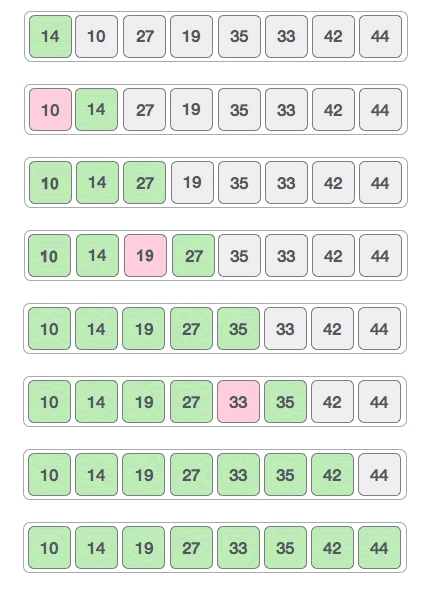
代码实现:
public class Demo {// list[N] 为存储待排序序列的数组public static void shell_sort(int[] list) {int length = list.length;// 初始化间隔数为 1int interval = 1;// 计算最大间隔while (interval < length / 3) {interval = interval * 3 + 1;}// 根据间隔数,不断划分序列,并对各子序列排序while (interval > 0) {// 对各个子序列做直接插入排序for (int i = interval; i < length; i++) {int temp = list[i];int j = i;while (j > interval - 1 && list[j - interval] >= temp) {list[j] = list[j - interval];j -= interval;}if (j != i) {list[j] = temp;}}// 计算新的间隔数,继续划分序列interval = (interval - 1) / 3;}}public static void main(String[] args) {int[] list = { 35, 33, 42, 10, 14, 19, 27, 44 };shell_sort(list);// 输出已排好序的序列for (int i = 0; i < list.length; i++) {System.out.print(list[i] + " ");}}}
执行结果:
11、归并排序算法
归并排序算法是在分治算法基础上设计出来的一种排序算法,它可以对指定序列完成升序(由小到大)或降序(由大到小)排序,对应的时间复杂度为O(nlogn)。
归并排序算法实现排序的思路是:
- 将整个待排序序列划分成多个不可再分的子序列,每个子序列中仅有 1 个元素;
- 所有的子序列进行两两合并,合并过程中完成排序操作,最终合并得到的新序列就是有序序列。
举个简单的例子,使用归并排序算法对 {7, 5, 2, 4, 1, 6, 3, 0} 实现升序排序的过程是:
1) 将 {7, 5, 2, 4, 1, 6, 3, 0} 分割成多个子序列,每个子序列中仅包含 1 个元素,分割过程如下所示: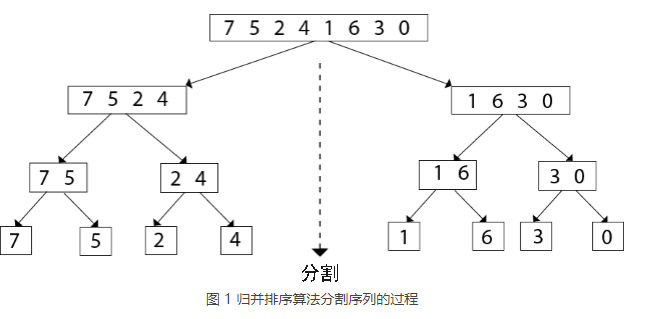
整个序列不断地被一分为二,最终被分割成 {7}、{5}、{2}、{4}、{1}、{6}、{3}、{0} 这几个序列。
2) 将 {7}、{5}、{2}、{4}、{1}、{6}、{3}、{0} 以“两两合并”的方式重新整合为一个有序序列,合并的过程如下图所示: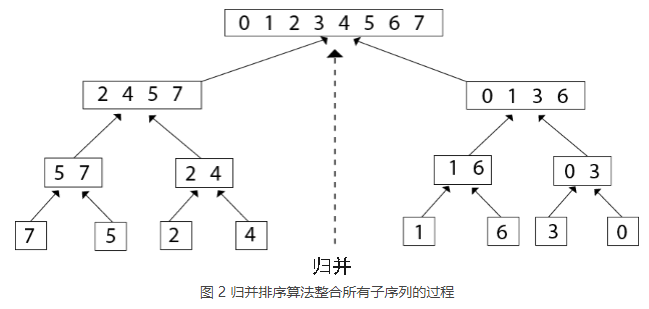
代码实现:
public class Demo {//实现归并排序算法的分割操作public static void merge_sort(int[] arr, int p, int q) {// 如果数组不存在或者 [p.q] 区域不合理if (arr == null || p >= q) {return;}//对[p,q]区域进行分割int mid = (p + q) / 2;merge_sort(arr, p, mid);merge_sort(arr, mid + 1, q);//对分割的 [p,mid] 和 [mid+1,q] 区域进行归并merge(arr, p, mid, q);}//实现归并排序算法的归并操作public static void merge(int[] arr, int p, int mid, int q) {int numL = mid - p + 1;int numR = q - mid;//创建 2 个数组,分别存储 [p,mid] 和 [mid+1,q]区域内的元素int[] leftarr = new int[numL + 1];int[] rightarr = new int[numR + 1];int i;for (i = 0; i < numL; i++) {leftarr[i] = arr[p - 1 + i];}//将 leftarr 数组中最后一个元素设置为足够大的数。leftarr[i] = 2147483647;for (i = 0; i < numR; i++) {rightarr[i] = arr[mid + i];}//将 rightarr 数组中最后一个元素设置为足够大的数。rightarr[i] = 2147483647;int j = 0;i = 0;//对 leftarr 和 rightarr 数组中存储的 2 个区域的元素做归并操作for (int k = p; k <= q; k++) {if (leftarr[i] <= rightarr[j]) {arr[k - 1] = leftarr[i];i++;} else {arr[k - 1] = rightarr[j];j++;}}}public static void main(String[] args) {int[] arr = new int[] { 7, 5, 2, 4, 1, 6, 3, 0 };//对 arr 数组中第 1 至 8 个元素进行归并排序merge_sort(arr, 1, 8);for (int i : arr) {System.out.print(i + " ");}}}
程序结果:
12、快速排序算法
提到排序算法,多数人最先想到的就是快速排序算法。快速排序算法是在分治算法基础上设计出来的一种排序算法,和其它排序算法相比,快速排序算法具有效率高、耗费资源少、容易实现等优点。
快速排序算法的实现思路是:
- 从待排序序列中任选一个元素(假设为 pivot)作为中间元素,将所有比 pivot 小的元素移动到它的左边,所有比 pivot 大的元素移动到它的右边;
- pivot 左右两边的子序列看作是两个待排序序列,各自重复执行第一步。直至所有的子序列都不可再分(仅包含 1 个元素或者不包含任何元素),整个序列就变成了一个有序序列。
真正实现快速排序算法时,我们通常会挑选待排序序列中第一个元素或者最后一个元素作为中间元素。
举个例子,使用快速排序算法对 {35, 33, 42, 10, 14, 19, 27, 44, 26, 31} 进行升序排序的过程为:
1) 选择序列中最后一个元素 31 作为中间元素,将剩余元素分为两个子序列,如下图所示:
分得的两个子序列是 {26, 27, 19, 10, 14} 和 {33, 44, 35, 42},前者包含的所有元素都比 31 小,后者包含的所有元素都比 31 大,两个子序列还可以再分。
2) 重复第一步,将 {26, 27, 19, 10, 14} 看作新的待排序序列:
- 选择最后一个元素 14 作为中间元素,将剩余元素分为 {10} 和 {19, 26, 27} 两个子序列。其中 {10} 仅有一个元素,无法再分;{19, 26, 27} 可以再分。
- 将 {19, 26, 27} 看作新的待排序序列,选择最后一个元素 27 作为中间元素,分得的两个子序列为 {19, 26} 和 {}。其中 {} 是空序列,无法再分;{19, 26} 可以再分。
- 将 {19, 26} 看作新的待排序序列,选择最后一个元素 26 作为中间元素,分得的两个子序列为 {19} 和 {},两个子序列都无法再分。
经过以上 3 步, {26, 27, 19, 10, 14} 子序列变成了 {10, 14, 19, 26, 27},这是一个有序的子序列。
3、重复第一步,将 {33, 44, 35, 42} 看作新的待排序序列:
- 选择最后一个元素 42 作为中间元素,将剩余元素分为 {33, 35} 和 {44} 两个子序列。其中 {33, 35} 可以再分;{44} 仅有一个元素,无法再分。
- 将 {33, 35} 看作新的待排序序列,选择最后一个元素 35 作为中间元素,分得的两个子序列为 {33} 和 {},两个子序列都无法再分。
经过以上 2 步, {33, 44, 35, 42} 子序列变成了 {33, 35, 42, 44},这是一个有序的子序列。
最终,原序列变成了 {10, 14, 19, 26, 27, 31, 33, 35, 42, 44},这是一个升序序列。
代码实现:
public class Demo {public static int partition(int[] arr, int p, int q) {int temp = 0;// lo、hi分别表示指向首个元素和倒数第 2 个元素的指针int lo = p;int hi = q - 1;// pivot 表示选中的中间值int pivot = arr[q];while (true) {// lo从左往右遍历,直至找到一个不小于 pivot 的元素while (arr[lo] < pivot) {lo++;}// hi从右往左遍历,直至找到一个不大于 pivot 的元素while (hi > 0 && arr[hi] > pivot) {hi--;}// 如果 lo≥hi,退出循环if (lo >= hi) {break;} else {// 交换 arr[lo] 和 arr[hi] 的值temp = arr[lo];arr[lo] = arr[hi];arr[hi] = temp;// lo 和 hi 都向前移动一个位置,准备继续遍历lo++;hi--;}}// 交换 arr[lo] 和 arr[q] 的值temp = arr[lo];arr[lo] = pivot;arr[q] = temp;// 返回中间值所在序列中的位置return lo;}public static void quick_sort(int[] arr, int p, int q) {//如果待排序序列不存在,或者仅包含 1 个元素,则不再进行分割if (q - p <= 0) {return;} else {//调用 partition() 函数,分割 [p,q] 区域int par = partition(arr, p, q);//以 [p,par-1]作为新的待排序序列,继续分割quick_sort(arr, p, par - 1);//以[par+1,q]作为新的待排序序列,继续分割quick_sort(arr, par + 1, q);}}public static void main(String[] args) {int[] arr = new int[] { 35, 33, 42, 10, 14, 19, 27, 44, 26, 31 };// 对于 arr 数组中所有元素进行快速排序quick_sort(arr, 0, 9);for (int i = 0; i < arr.length; i++) {System.out.print(arr[i]+" ");}}}
程序结果:
13、计数排序算法
假设待排序序列为 {4, 2, 2, 8, 3, 3, 1},使用计数排序算法完成升序排序的过程为:
1) 找到序列中的最大值(用 max 表示)。对于 {4, 2, 2, 8, 3, 3, 1} 序列来说,最大值是 8。
2) 创建一个长度为 max+1、元素初值全部为 0 的数组(Python 中可以使用列表),为数组中 [1,max] 区域内的各个空间建立索引:
找到序列中的最小值(用 min 表示),作为数组下标为 1 的存储空间的索引;
- 将 max 作为数组下标为 max 的存储空间的索引;
- 将 max-1 作为数组下标为 max-1 的存储空间的索引;
- 将 max-2 作为数组下标为 max-2 的存储空间的索引;
- ……
为某个存储空间建立索引,其实就是为这个存储空间贴上一个独一无二的标签,借助索引(标签),我们可以快速地找到此空间并访问内部的数据。
本例中,待排序的元素都是整数,可以直接将数组下标作为各个存储空间的索引,如下图所示。
对于长度为 max+1 的数组,计数排序算法的实现过程不会用到下标为 0 的数组空间。
3) 统计待排序序列中各个元素的出现次数,存储到以该元素为索引的数组空间中。例如,待排序序列中元素 2 出现了两次,所以索引(下标)为 2 的数组空间中存储 2 。更新后的数组如下图所示:
4) 进一步加工数组中存储的数据。从数组下标为 1 的位置开始,按照如下公式修改数组中存储的元素:
array[i] = array[i-1] + array[i]
其中 i 的取值范围是 [1, max],修改后的数组为:
5) 遍历待排序列中的元素,以该元素为索引获取数组中存储的值,此值即为序列排序后元素应处的位置。
举个例子,序列中第一个元素是 4,数组中索引 4 对应的值为 6,因此序列排序后元素 4 位于第 6 的位置处,如下图所示: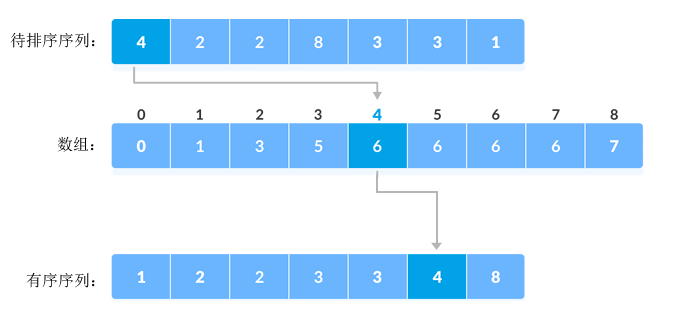
6) 当确定了一个元素排序后的位置,需要将数组中该元素为索引对应的值减去 1。
例如,我们已经确定了第二个元素 2 在有序序列中位于第 2 个位置,此时将数组下标为 2 处的值减去 1(3-1=2),则数组中第 3 个元素 2 位于有序序列中第 1 的位置上。
以上 6 步就是计数排序算法的整个实现思路,对应的时间复杂度为O(n)。
代码实现:
public class Demo {//找到数组中的最大值public static int getMax(int[] list) {int max = list[0];for (int i = 1; i < list.length; i++) {if (list[i] > max) {max = list[i];}}return max;}public static void countingSort(int[] list) {int length = list.length;//第 1 步,找到序列中的最大值int max = getMax(list);//第 2 步,初始化一个 array[max+1]int[] array = new int[max + 1];int[] output = new int[length];//第 3 步,统计各个元素的出现次数,并存储在相应的位置上for (int i = 0; i < length; i++) {array[list[i]]++;}// 第 4 步,累加 array 数组中的出现次数for (int i = 1; i <= max; i++) {array[i] += array[i - 1];}// 第 5 步,根据 array 数组中的信息,找到各个元素排序后所在位置,存储在 output 数组中for (int i = length - 1; i >= 0; i--) {output[array[list[i]] - 1] = list[i];array[list[i]]--;}// 将 output 数组中的数据原封不动地拷贝到 list 数组中for (int i = 0; i < length; i++) {list[i] = output[i];}}public static void printList(int[] list) {for (int i = 0; i < list.length; i++) {System.out.print(list[i] + " ");}}public static void main(String[] args) {// 待排序序列int[] list = new int[] { 4, 2, 2, 8, 3, 3, 1 };//进行计数排序countingSort(list);printList(list);}}
程序结果:
14、基数排序算法
基数排序算法适用于对多个整数或者多个字符串进行升序或降序排序,例如:
121, 432, 564, 23, 1, 45, 788
“zhangsan”、”lisi”、”wangwu”
一个整数由多个数字组成,例如 123 由 1、2、3 这 3 个数字组成;一个字符串由多个字符组成,例如 “lisi” 由 “l”、”i”、”s”、”i” 这 4 个字符组成。基数排序算法的实现思路是:对于待排序序列中的各个元素,依次比较它们包含的各个数字或字符,根据比较结果调整各个元素的位置,最终就可以得到一个有序序列。
对于待排序的整数序列,依次比较各个整数的个位数、十位数、百位数……,数位不够的用 0 表示;对于待排序的字符串序列,依次比较各个字符串的第一个字符、第二个字符、第三个字符……,位数不够的用 NULL 表示。
举个例子,使用基数排序算法对 {121, 432, 564, 23, 1, 45, 788} 进行升序排序,需要经历下图所示的三个过程:
依次比较各个元素中的个位数字、十位数字和百位数字,每次根据比较结果对所有元素进行升序排序,最终就可以得到一个升序序列。
实现细节
通过前面的实例,相信大家已经了解了基数排序算法的实现思路。接下来,我们给大家讲解实现基数排序算法的具体细节。
仍以对 {121, 432, 564, 23, 1, 45, 788} 进行升序排序为例,基数排序算法的具体实现过程如下:
1) 找到序列中的最大值(如果是字符串序列,找序列中最长的字符串),记录它的位数。通过观察不难判断,整个序列中的最大值为 788,它由 3 个数字组成。这就意味着,算法中需要依次根据各元素的个位数、十位数和百位数对所有元素进行排序。
2) 找到序列中所有元素的个位数,采用计数排序算法对它们进行排序,如下图所示:
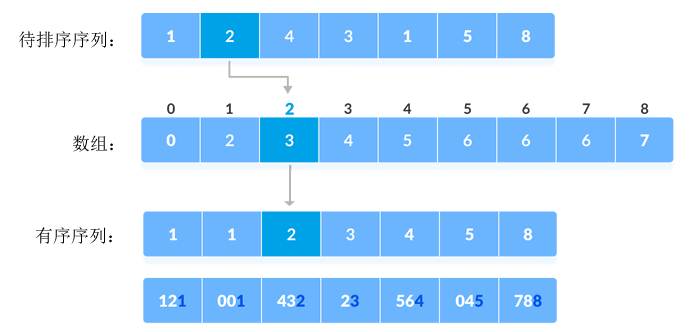
图 2 根据个位数对序列进行升序排序
数组中记录的是各个元素在有序序列中的位置,以元素 2 为例,数组中存储的值是 3,表示它作为有序序列中的第 3 个元素。由待排序序列推导出数组的具体过程,大家可以阅读《计数排序算法》一节。
根据个位数的大小关系,{121, 432, 564, 23, 1, 45, 788} 进行了重新排序,得到的新序列为 {121, 1, 432, 23, 564, 45, 788}。
3) 找到 {121, 1, 432, 23, 564, 45, 788} 中所有元素的十位数,以同样的方式进行排序,得到的新序列为 {1, 121,. 23, 432, 45, 564, 788}。
4) 找到 {1, 121, 23, 432, 45, 564, 788} 中所有元素的百位数,继续以同样的方法进行排序,得到的新序列为 {1, 23, 45, 121, 432, 564, 788}。
经过以上几个步骤,最终完成了对 {121, 432, 564, 23, 1, 45, 788} 序列的升序排序。
代码实现:
public class Demo {// 计数排序算法,place 表示以指定数位为准,对序列中的元素进行排序public static void countingSort(int array[], int place) {int size = array.length;int[] output = new int[size];// 假设第一个元素指定数位上的值最大int max = (array[0] / place) % 10;// 找到真正数位上值最大的元素for (int i = 1; i < size; i++) {if (((array[i] / place) % 10) > max)max = array[i];}// 创建并初始化 count 数组int[] count = new int[max + 1];for (int i = 0; i < max; ++i)count[i] = 0;// 统计各个元素出现的次数for (int i = 0; i < size; i++)count[(array[i] / place) % 10]++;// 累加 count 数组中的出现次数for (int i = 1; i < 10; i++)count[i] += count[i - 1];// 根据 count 数组中的信息,找到各个元素排序后所在位置,存储在 output 数组中for (int i = size - 1; i >= 0; i--) {output[count[(array[i] / place) % 10] - 1] = array[i];count[(array[i] / place) % 10]--;}// 将 output 数组中的数据原封不动地拷贝到 array 数组中for (int i = 0; i < size; i++)array[i] = output[i];}// 找到整个序列中的最大值public static int getMax(int array[]) {int size = array.length;int max = array[0];for (int i = 1; i < size; i++)if (array[i] > max)max = array[i];return max;}// 基数排序算法public static void radixSort(int array[]) {// 找到序列中的最大值int max = getMax(array);// 根据最大值具有的位数,从低位依次调用计数排序算法for (int place = 1; max / place > 0; place *= 10)countingSort(array, place);}public static void main(String args[]) {int[] data = { 121, 432, 564, 23, 1, 45, 788 };radixSort(data);System.out.println(Arrays.toString(data));}}
程序结果:
15、桶排序算法
桶排序(又称箱排序)是一种基于分治思想、效率很高的排序算法,理想情况下对应的时间复杂度为 O(n)。
实现思路
假设一种场景,对 {5, 2, 1, 4, 3} 进行升序排序,桶排序算法的实现思路是:
- 准备 5 个桶,从 1~5 对它们进行编号;
- 将待排序序列的各个元素放置到相同编号的桶中;
- 从 1 号桶开始,依次获取桶中放置的元素,得到的就是一个升序序列。
整个实现思路如下图所示: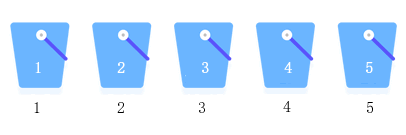
桶排序算法中,待排序的数据量和桶的数量并不一定是简单的“一对一”的关系,更多场景中是“多对一”的关系,例如,使用桶排序算法对 {11, 9, 21, 8, 17, 19, 13, 1, 24, 12} 进行升序排序,实现过程如下图所示: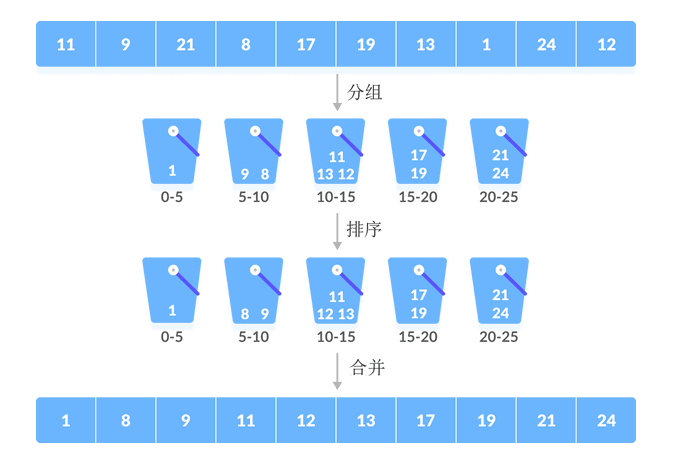
待排序序列中有 10 个元素,但算法中只用了 5 个桶,因此有些桶需要存放多个元素。实际场景中,我们可以自定义各个桶存放元素的区间(范围),比如上图中第一个桶存放 [0,5) 区间内的元素,第二个桶存放 [6,10) 之间的元素。
当存在“一个桶中有多个元素”的情况时,要先使用合适的排序算法对各个痛内的元素进行排序,然后再根据桶的次序逐一取出所有元素,最终得到的才是一个有序序列。
总之,桶排序算法的实现思路是:将待排序序列中的元素根据规则分组,每一组采用快排、插入排序等算法进行排序,然后再按照次序将所有元素合并,就可以得到一个有序序列。
具体实现
假设用桶排序算法对 {0.42, 0.32, 0.23, 0.52, 0.25, 0.47, 0.51} 进行升序排序,采用的分组规则是:将所有元素分为 10 组,每组的标号分别为 0~9。对序列中的各个元素乘以 10 再取整,得到的值即为该元素所在组的组号。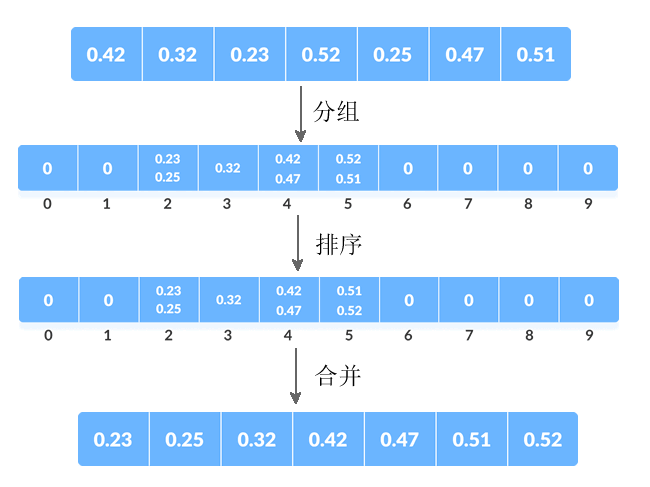
代码实现:
import java.util.ArrayList;import java.util.Collections;public class BucketSort {public static void bucketSort(float[] arr) {int n = arr.length;if (n <= 0)return;@SuppressWarnings("unchecked")ArrayList<Float>[] bucket = new ArrayList[n];// 创建空桶for (int i = 0; i < n; i++)bucket[i] = new ArrayList<Float>();// 根据规则将序列中元素分散到桶中for (int i = 0; i < n; i++) {int bucketIndex = (int) arr[i] * n;bucket[bucketIndex].add(arr[i]);}// 对各个桶内的元素进行排序for (int i = 0; i < n; i++) {Collections.sort((bucket[i]));}// 合并所有桶内的元素int index = 0;for (int i = 0; i < n; i++) {for (int j = 0, size = bucket[i].size(); j < size; j++) {arr[index++] = bucket[i].get(j);}}}public static void main(String[] args) {float[] arr = { (float) 0.42, (float) 0.32, (float) 0.23, (float) 0.52, (float) 0.25, (float) 0.47,(float) 0.51 };bucketSort(arr);for (float i : arr)System.out.print(i + " ");}}
程序结果:
16、稳定排序算法
给定的待排序序列中,经常会包含相同的元素,例如:
3 1 2 4 2
此序列中包含两个元素 2,为了区分它们,我们分别称它们为 “红 2” 和 “绿 2”。
评价一个排序算法是否稳定,是指该算法完成排序的同时,是否会改变序列中相同元素的相对位置。例如,上面序列中红 2 和绿 2 的相对位置是:红 2 位于绿 2 的左侧,或者说绿 2 位于红 2 的右侧。如果使用某个排序算法对序列进行排序,得到的有序序列是:
升序序列:
1 2 2 3 4
降序序列:
4 3 2 2 1
红 2 依然位于绿 2 的左侧,这个排序算法就是稳定的;反之,如果红 2 和绿 2 的相对位置发生了改变,这个排序算法就是不稳定的。
下表给大家列出了常用的排序算法以及它们的稳定性:
| 排序算法 | 稳定排序算法 |
|---|---|
| 冒泡排序算法 | 稳定 |
| 插入排序算法 | 稳定 |
| 希尔排序算法 | 不稳定 |
| 选择排序算法 | 不稳定 |
| 归并排序算法 | 稳定 |
| 快速排序算法 | 不稳定 |
| 计数排序算法 | 不稳定 |
| 基数排序算法 | 不稳定 |
| 桶排序算法 | 不稳定 |
通过优化代码、改进实现思路等方式,某些 “不稳定” 的算法也可以变得 “稳定”。以桶排序算法为例,如果保证各个桶内存储相同元素时不改变它们的相对位置,且桶内排序时采用稳定的排序算法,那么桶排序算法就可以变得“稳定”。
【扩展】就地排序算法
除了稳定性,某些场景中还需要使用就地排序算法。
“就地排序”的含义是:排序算法在排序过程中,主要使用待排序序列占用的内存空间,最多额外创建几个辅助变量,不再申请过多的辅助空间。也就是说,就地排序算法指的是直接将待排序序列修改成有序序列的排序算法,而不是新创建一个有序序列。
就地排序算法的空间复杂度为 O(1)。
下表给大家罗列了哪些排序算法属于就地排序算法:
| 排序算法 | 就地排序算法 |
|---|---|
| 冒泡排序算法 | 是 |
| 插入排序算法 | 是 |
| 希尔排序算法 | 是 |
| 选择排序算法 | 是 |
| 归并排序算法 | 不是 |
| 快速排序算法 | 是 |
| 计数排序算法 | 不是 |
| 基数排序算法 | 不是 |
| 桶排序算法 | 不是 |
17、顺序查找算法
顺序查找算法又称顺序搜索算法或者线性搜索算法,是所有查找算法中最基本、最简单的,对应的时间复杂度为O(n)。
顺序查找算法适用于绝大多数场景,既可以在有序序列中查找目标元素,也可以在无序序列中查找目标元素。
实现思路:
所谓顺序查找,指的是从待查找序列中的第一个元素开始,查看各个元素是否为要找的目标元素。
举个简单的例子,采用顺序查找算法在 {10,14,19,26,27,31,33,35,42,44} 序列中查找 33,整个查找过程如下图所示:

图 1 顺序查找 33 的过程
结合图 1,顺序查找算法会遍历整个待查找序列,序列中的每个元素都会和目标元素进行比对,直至找到 33。如果遍历完整个序列仍没有找到与 33 相等的元素,表明序列中不包含目标元素,查找失败。
代码实现:
public class Demo {// 实现顺序查找,arr[N] 为待查找序列,value 为要查找的目标元素public static int linear_search(int[] arr, int value) {// 从第 1 个元素开始遍历for (int i = 0; i < arr.length; i++) {// 匹配成功,返回元素所处的位置下标if (arr[i] == value) {return i;}}// 匹配失败,返回 -1return -1;}public static void main(String[] args) {int[] arr = new int[] { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };int add = linear_search(arr, 33);if (add != -1) {System.out.println("查找成功,为序列中第 " + (add + 1) + " 个元素");} else {System.out.println("查找失败");}}}
程序结果:
18、二分查找算法
二分查找又称折半查找、二分搜索、折半搜索等,是在分治算法基础上设计出来的查找算法,对应的时间复杂度为O(logn)。
二分查找算法仅适用于有序序列,它只能用在升序序列或者降序序列中查找目标元素。
实现思路:
在有序序列中,使用二分查找算法搜索目标元素的核心思想是:不断地缩小搜索区域,降低查找目标元素的难度。
以在升序序列中查找目标元素为例,二分查找算法的实现思路是:
- 初始状态下,将整个序列作为搜索区域(假设为 [B, E]);
- 找到搜索区域内的中间元素(假设所在位置为 M),和目标元素进行比对。如果相等,则搜索成功;如果中间元素大于目标元素,表明目标元素位于中间元素的左侧,将 [B, M-1] 作为新的搜素区域;反之,若中间元素小于目标元素,表明目标元素位于中间元素的右侧,将 [M+1, E] 作为新的搜素区域;
- 重复执行第二步,直至找到目标元素。如果搜索区域无法再缩小,且区域内不包含任何元素,表明整个序列中没有目标元素,查找失败。
举个简单的例子,在下图所示的升序序列中查找元素 31。
二分查找算法的具体实现过程为:
1) 初始状态下,搜索区域是整个序列。找到搜索区域内的中间元素。指定区域内中间元素的位置可以套用如下公式求出:
Mid = ⌊ Begin + (End - Begin) / 2 ⌋
End 表示搜索区域内最后一个元素所在位置,Begin 表示搜索区域内第一个元素所在的位置,Mid 表示中间元素所在的位置。
图 1 中,所有元素的位置分别用 0~9 表示,中间元素的位置为 ⌊ 0 + (9 - 0) / 2 ⌋ = 4,如下图所示: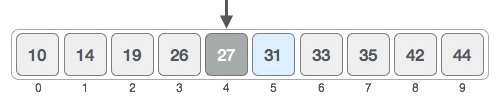
中间元素 27 < 31,可以断定 [0, 4] 区域内绝对没有 31,目标元素只可能位于 [5, 9] 区域内,如下图所示:
2) 在 [5, 9] 区域内,中间元素的位置为 ⌊ 5 + (9 - 5) / 2 ⌋ = 7,如下图所示: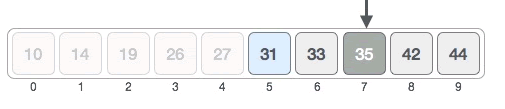
中间元素 35 > 31,可以断定 [7, 9] 区域内绝对没有 31,目标元素只可能位于 [5,6] 中,如下图所示:
3) 在 [5, 6] 区域内,中间元素的位置为 ⌊ 5 + (6- 5) / 2 ⌋ = 5,中间元素就是 31,成功找到目标元素。
代码实现:
public class Demo {// 实现二分查找算法,ele 表示要查找的目标元素,[p,q] 指定查找区域public static int binary_search(int[] arr, int p, int q, int ele) {// 如果[p,q] 不存在,返回 -1if (p > q) {return -1;}// 找到中间元素所在的位置int mid = p + (q - p) / 2;// 递归的出口if (ele == arr[mid]) {return mid;}// 比较 ele 和 arr[mid] 的值,缩小 ele 可能存在的区域if (ele < arr[mid]) {// 新的搜索区域为 [p,mid-1]return binary_search(arr, p, mid - 1, ele);} else {// 新的搜索区域为 [mid+1,q]return binary_search(arr, mid + 1, q, ele);}}public static void main(String[] args) {int[] arr = new int[] { 10, 14, 19, 26, 27, 31, 33, 35, 42, 44 };// 输出二叉查找元素 31 所在位置的下标int add = binary_search(arr, 0, 9, 31);System.out.print(add);}}
程序结果:
19、插值查找算法
对于已经学过二分查找算法的读者来说,学习插值查找算法会变得非常容易,因为插值查找算法完全照搬了二分查找算法的解题思路,仅对一些实现细节做了修改。
首先,我们通过一个实例回忆一下二分查找算法的解题思路。例如,在 {1,2,3,4,5,6,7,8,9,10} 升序序列中查找元素 2,二分查找算法的查找过程如下图所示:
图 1 二分查找算法的实现过程
如图 1 所示,先找到搜索区域中的中间元素,然后和目标元素进行比较,如果相同表示查找成功;反之,根据比较结果选择中间元素左侧或右侧的区域作为新的搜索区域,以同样的方式继续查找。
插值查找算法的解题思路和二分查找算法几乎相同,唯一的区别在于,每次与目标元素做比较的元素并非搜索区域内的中间元素,此元素的位置需要通过如下公式计算得出:
Mid = Begin + ( (End - Begin) / (A[End] - A[Begin]) ) * (X - A[Begin])
式子中,各部分的含义分别是:
- Mid:计算得出的元素的位置;
- End:搜索区域内最后一个元素所在的位置;
- Begin:搜索区域内第一个元素所在的位置;
- X:要查找的目标元素;
- A[]:表示整个待搜索序列。
为了方便讲解,我们仍将 Mid 位置上的元素称为 “中间元素”。
使用插值查找算法在 {1,2,3,4,5,6,7,8,9,10} 升序序列中查找元素 2,查找过程如下:
1) 假设序列中各个元素的位置为 0~9,搜索区域为整个序列,通过公式计算出 “中间元素” 的位置:
Mid = 0 + ( (9-0)/(10-1) ) * (2-1) = 1
“中间元素” 的位置为 1,也就是元素 2,显然这是我们要找的目标元素,查找结束。整个查找过程如下所示:
图 2 插值查找算法的实现过程
对比图 1 和图 2 不难看出,在 {1, 2, 3, 4, 5, 6, 7, 8, 9, 10} 这个满足均匀分布的升序序列中查找元素 2,插值查找算法的执行效率要优于二分查找算法。
代码实现:
public class Demo {// 实现插值查找算法,ele 表示要查找的目标元素,[begin,end] 指定查找区域public static int interpolation_search(int[] arr, int begin, int end, int ele) {// 如果[begin,end] 不存在,返回 -1if (begin > end) {return -1;}//如果搜索区域内只有一个元素,判断其是否为目标元素if (begin == end) {if (ele == arr[begin]) {return begin;}//如果该元素非目标元素,则查找失败return -1;}// 找到中间元素所在的位置int mid = begin + ((end - begin) / (arr[end] - arr[begin]) * (ele - arr[begin]));// 递归的出口if (ele == arr[mid]) {return mid;}// 比较 ele 和 arr[mid] 的值,缩小 ele 可能存在的区域if (ele < arr[mid]) {// 新的搜索区域为 [begin,mid-1]return interpolation_search(arr, begin, mid - 1, ele);} else {// 新的搜索区域为 [mid+1,end]return interpolation_search(arr, mid + 1, end, ele);}}public static void main(String[] args) {int[] arr = new int[] { 1, 2, 3, 4, 5, 6, 7, 8, 9, 10 };// 输出目标元素 2 所在位置的下标int add = interpolation_search(arr, 0, 9, 2);if(add != -1) {System.out.print(add);}else {System.out.print("查找失败");}}}
程序结果:
20、哈希查找算法
哈希查找算法又称散列查找算法,是一种借助哈希表(散列表)查找目标元素的方法,查找效率最高时对应的时间复杂度为 O(1)。
哈希表(Hash table)又称散列表,是一种存储结构,通常用来存储多个元素。
和其它存储结构(线性表、树等)相比,哈希表查找目标元素的效率非常高。每个存储到哈希表中的元素,都配有一个唯一的标识(又称“索引”或者“键”),用户想查找哪个元素,凭借该元素对应的标识就可以直接找到它,无需遍历整个哈希表。
多数场景中,哈希表是在数组的基础上构建的,下图给大家展示了一个普通的数组:
图 1 数组
使用数组构建哈希表,最大的好处在于:可以直接将数组下标当作已存储元素的索引,不再需要为每个元素手动配置索引,极大得简化了构建哈希表的难度。
我们知道,在数组中查找一个元素,除非提前知晓它存储位置处的下标,否则只能遍历整个数组。哈希表的解决方案是:各个元素并不从数组的起始位置依次存储,它们的存储位置由专门设计的函数计算得出,我们通常将这样的函数称为哈希函数。
哈希函数类似于数学中的一次函数,我们给它传递一个元素,它反馈给我们一个结果值,这个值就是该元素对应的索引,也就是存储到哈希表中的位置。
举个例子,将 {20, 30, 50, 70, 80} 存储到哈希表中,我们设计的哈希函数为 y=x/10,最终各个元素的存储位置如下图所示: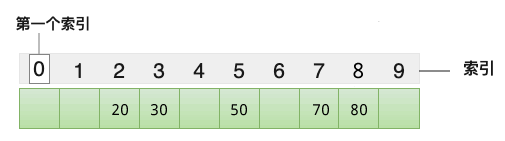
图 2 哈希表存储结构
在图 2 的基础上,假设我们想查找元素 50,只需将它带入 y=x/10 这个哈希函数中,计算出它对应的索引值为 5,直接可以在数组中找到它。借助哈希函数,我们提高了数组中数据的查找效率,这就是哈希表存储结构。
构建哈希表时,哈希函数的设计至关重要。假设将 {5, 20, 30, 50, 55} 存储到哈希表中,哈希函数是 y=x%10,各个元素在数组中的存储位置如下图所示: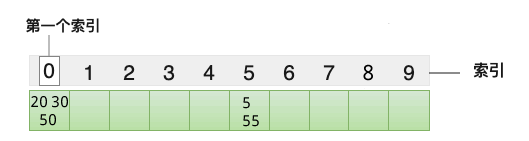
图 3 哈希表发生哈希冲突
可以看到,5 和 55 以及 20、30 和 50 对应的索引值是相同的,它们的存储位置发生了冲突,我们习惯称为哈希冲突或者哈希碰撞。设计一个好的哈希函数,可以降低哈希冲突的出现次数。哈希表提供了很多解决哈希冲突的方案,比如线性探测法、再哈希法、链地址法等。
本节我们使用线性探测法解决哈希冲突,解决方法是:当元素的索引值(存储位置)发生冲突时,从当前位置向后查找,直至找到一个空闲位置,作为冲突元素的存储位置。仍以图 3 中的哈希表为例,使用线性探测法解决哈希冲突的过程是:
- 元素 5 最先存储到数组中下标为 5 的位置;
- 元素 20 最先存储到数组中下标为 0 的位置;
- 元素 30 的存储位置为 0,和 20 冲突,根据线性探测法,从下标为 0 的位置向后查找,下标为 1 的存储位置空闲,用来存储 30;
- 元素 50 的存储位置为 0,和 20 冲突,根据线性探测法,从下标为 0 的位置向后查找,下标为 2 的存储位置空闲,用来存储 50;
- 元素 55 的存储位置为 5,和 5 冲突,根据线性探测法,从下标为 5 的位置向后查找,下标为 6 的存储位置空闲,用来存储 55。
借助线性探测法,最终 {5, 20, 30, 50, 55} 存储到哈希表中的状态为: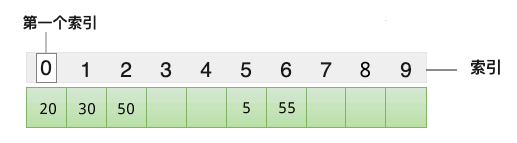
图 4 线性探测法解决哈希冲突
假设我们从图 4 所示的哈希表中查找元素 50,查找过程需要经过以下几步:
- 根据哈希函数 y=x%10,目标元素的存储位置为 0,但经过和下标为 0 处的元素 20 比较,该位置存储的并非目标元素;
- 根据线性探测法,比较下标位置为 1 处的元素 30,也不是目标元素;
- 继续比较下标位置为 2 的元素 50,成功找到目标元素。
对于发生哈希冲突的哈希表,尽管查找效率会下降,但仍比一些普通存储结构(比如数组)的查找效率高。
代码实现:
public class Demo {//哈希函数public static int hash(int value) {return value % 10;}//创建哈希表public static void creatHash(int [] arr,int [] hashArr) {int i,index;//将序列中每个元素存储到哈希表for (i = 0; i < 5; i++) {index = hash(arr[i]);while(hashArr[index % 10] != 0) {index++;}hashArr[index] = arr[i];}}//实现哈希查找算法public static int hash_serach(int [] hashArr,int value) {//查找目标元素对应的索引值int hashAdd = hash(value);while (hashArr[hashAdd] != value) { // 如果索引位置不是目标元素,则发生了碰撞hashAdd = (hashAdd + 1) % 10; // 根据线性探测法,从索引位置依次向后探测//如果探测位置为空,或者重新回到了探测开始的位置(即探测了一圈),则查找失败if (hashArr[hashAdd] == 0 || hashAdd == hash(value)) {return -1;}}//返回目标元素所在的数组下标return hashAdd;}public static void main(String[] args) {int [] arr = new int[] {5, 20, 30, 50, 55};int[] hashArr = new int[10];//创建哈希表creatHash(arr,hashArr);// 查找目标元素 50 位于哈希表中的位置int hashAdd = hash_serach(hashArr,50);if(hashAdd == -1) {System.out.print("查找失败");}else {System.out.print("查找成功,目标元素所在哈希表中的下标为:" + hashAdd);}}}
程序结果:
21、最小生成树
数据结构提供了 3 种存储结构,分别称为线性表、树和图,如图 1 所示。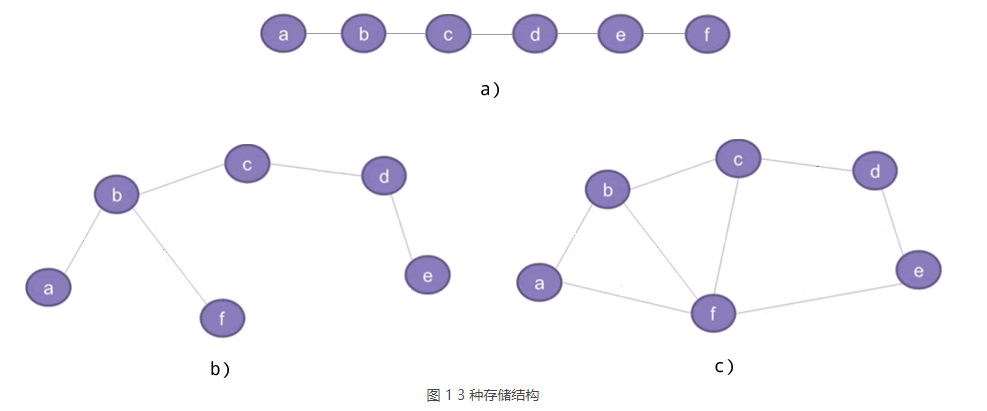
a) 是线性表,b) 是树,c) 是图。 在图存储结构中,a、b、c 等称为顶点,连接顶点的线称为边。
线性表是最简单的存储结构,很容易分辨。树和图有很多相似之处,它们的区别是:树存储结构中不允许存在环路,而图存储结构中可以存在环路(例如图 1 c) 中,c-b-f-c、b-a-f-b 等都是环路)。
本节要讲的最小生成树和图存储结构息息相关,接下来我们将结合图存储结构,给大家讲解什么是生成树,以及什么是最小生成树。
生成树
根据所有顶点之间是否存在通路,图存储结构可以细分为连通图和非连通图。举个例子: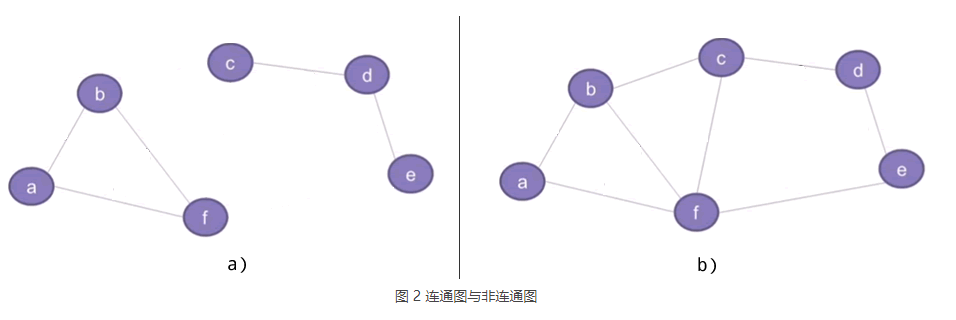
图 2 a) 是一个非连通图,比如图中找不到一条从 a 到 c 的路径。图 2 b) 是一个连通图,因为从一个顶点到另一个顶点都至少存在一条通路,比如从 a 到 c 的通路可以为 a-f-c、a-b-c 等。
所谓生成树,指的是具备以下条件的连通图:
- 包含图中所有的顶点;
- 任意顶点之间有且仅有一条通路。
图 2 b) 是一个连通图,其对应的生成树有很多种,例如: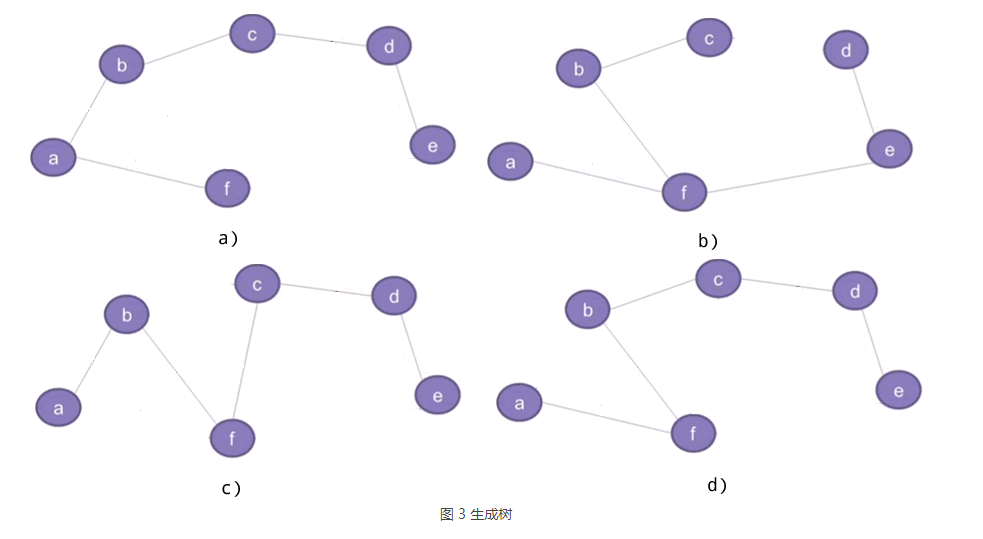
图 2 b) 对应的生成树还有很多,图 3 仅给大家列出了其中的 4 种。也就是说,一个连通图可能对应着多种不同的生成树。
最小生成树
借助生成树,可以解决实际生活中的很多问题。例如,为了方便 6 座城市中居民的生产和生活,政府要在 6 座城市之间修建公路。本着节约资金的原则,6 座城市只需要建立 5 条公路即可实现连通,如何修建公路才能最大程度上节省资金呢?
我们将 6 座城市分别用 a~f 表示,6 座城市之间可以修建的公路以及所需资金如下图所示: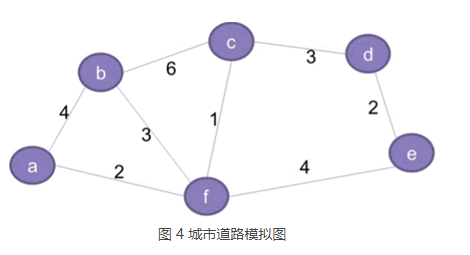
a~f 这 6 个顶点各自代表一座城市,连接两个顶点的边代表两座城市之间可以修建公路,每条边对应的数值称为权,表示修建公路所需要的资金。
如图 4 所示,在连通图的基础上,我们赋予每条边一个数值,这样的连通图又称连通网。一个连通网对应生成树可能有多种,每个生成树中所有边的权值的总和,就是这个生成树的总权值。例如结合图 4 ,图 3 a) 生成树的总权值为 17,图 3 c) 的总权值为 13。
最小生成树指的就是在连通网中找到的总权值最小的生成树。在连通图查找最小生成树,常用的算法有两种,分别称为普里姆算法和克鲁斯卡尔算法,您可以点击它们做详细地了解。
22、普里姆算法
了解了什么是最小生成树后,本节为您讲解如何用普里姆(prim)算法查找连通网(带权的连通图)中的最小生成树。
普里姆算法查找最小生成树的过程,采用了贪心算法的思想。对于包含 N 个顶点的连通网,普里姆算法每次从连通网中找出一个权值最小的边,这样的操作重复 N-1 次,由 N-1 条权值最小的边组成的生成树就是最小生成树。
那么,如何找出 N-1 条权值最小的边呢?普里姆算法的实现思路是:
- 将连通网中的所有顶点分为两类(假设为 A 类和 B 类)。初始状态下,所有顶点位于 B 类;
- 选择任意一个顶点,将其从 B 类移动到 A 类;
- 从 B 类的所有顶点出发,找出一条连接着 A 类中的某个顶点且权值最小的边,将此边连接着的 A 类中的顶点移动到 B 类;
- 重复执行第 3 步,直至 B 类中的所有顶点全部移动到 A 类,恰好可以找到 N-1 条边。
举个例子,下图是一个连通网,使用普里姆算法查找最小生成树,需经历以下几个过程: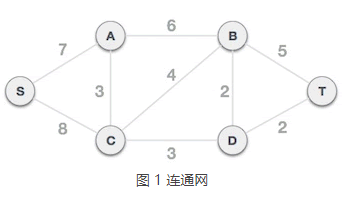
1) 将图中的所有顶点分为 A 类和 B 类,初始状态下,A = {},B = {A, B, C, D, S, T}。
2) 从 B 类中任选一个顶点,假设选择 S 顶点,将其从 B 类移到 A 类,A = {S},B = {A, B, C, D, T}。从 A 类的 S 顶点出发,到达 B 类中顶点的边有 2 个,分别是 S-A 和 S-C,其中 S-A 边的权值最小,所以选择 S-A 边组成最小生成树,将 A 顶点从 B 类移到 A 类,A = {S, A},B = {B, C, D, T}。
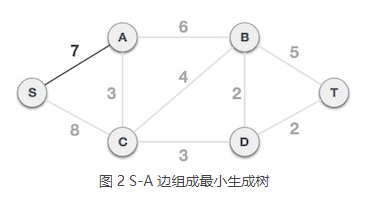
3) 从 A 类中的 S、A 顶点出发,到达 B 类中顶点的边有 3 个,分别是 S-C、A-C、A-B,其中 A-C 的权值最小,所以选择 A-C 组成最小生成树,将顶点 C 从 B 类移到 A 类,A = {S, A, C},B = {B, D, T}。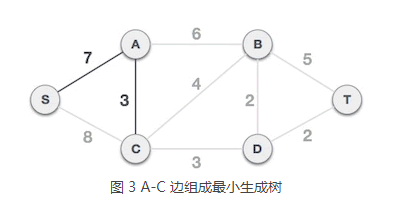
4) 从 A 类中的 S、A、C 顶点出发,到达 B 类顶点的边有 S-C、A-B、C-B、C-D,其中 C-D 边的权值最小,所以选择 C-D 组成最小生成树,将顶点 D 从 B 类移到 A 类,A = {S, A, C, D},B = {B, T}。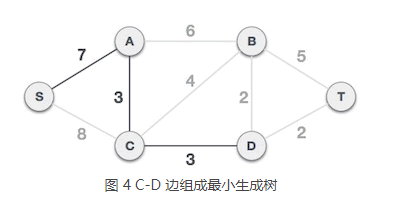
5) 从 A 类中的 S、A、C、D 顶点出发,到达 B 类顶点的边有 A-B、C-B、D-B、D-T,其中 D-B 和 D-T 的权值最小,任选其中的一个,例如选择 D-B 组成最小生成树,将顶点 B 从 B 类移到 A 类,A = {S, A, C, D, B},B = {T}。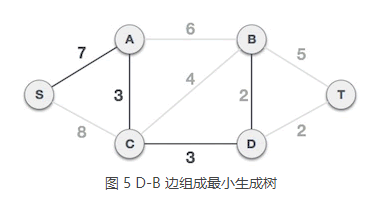
6) 从 A 类中的 S、A、C、D、B 顶点出发,到达 B 类顶点的边有 B-T、D-T,其中 D-T 的权值最小,选择 D-T 组成最小生成树,将顶点 T 从 B 类移到 A 类,A = {S, A, C, D, B, T},B = {}。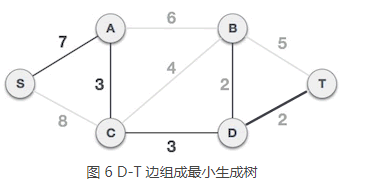
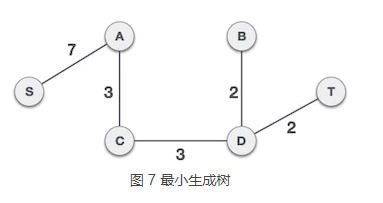
7) 由于 B 类中的顶点全部移到了 A 类,因此 S-A、A-C、C-D、D-B、D-T 组成的是一个生成树,而且是一个最小生成树,它的总权值为 17。
普里姆算法的具体实现
import java.util.Scanner;public class prim {static int V = 6;public static int min_Key(int []key,boolean []visited) {//遍历 key 数组使用,min 记录最小的权值,min_index 记录最小权值关联的顶点int min = 2147483647,min_index = 0;//遍历 key 数组for (int v = 0; v < V; v++) {//如果当前顶点为被选择,且对应的权值小于 min 值if (visited[v] == false && key[v] < min) {//更新 min 的值并记录该顶点的位置min = key[v];min_index = v;}}//返回最小权值的顶点的位置return min_index;}public static void print_MST(int []parent, int [][]cost) {int minCost = 0;System.out.println("最小生成树为:");//遍历 parent 数组for (int i = 1; i < V; i++) {//parent 数组下标值表示各个顶点,各个下标对应的值为该顶点的父节点System.out.println((parent[i]+1)+" - "+(i+1)+" wight:"+cost[i][parent[i]]);//由于数组下标从 0 开始,因此输出时各自 +1//统计最小生成树的总权值minCost += cost[i][parent[i]];}System.out.print("总权值为:"+minCost);}public static void find_MST(int [][]cost) {//key 数组用于记录 B 类顶点到 A 类顶点的权值//parent 数组用于记录最小生成树中各个顶点父节点的位置,便于最终生成最小生成树//visited 数组用于记录各个顶点属于 A 类还是 B 类int []parent = new int[V];int []key = new int[V];boolean []visited=new boolean[V];// 初始化 3 个数组for (int i = 0; i < V; i++) {key[i] = 2147483647; // 将 key 数组各个位置设置为无限大的数visited[i] = false; // 所有的顶点全部属于 B 类parent[i] = -1; // 所有顶点都没有父节点}// 选择 key 数组中第一个顶点,开始寻找最小生成树key[0] = 0; // 该顶点对应的权值设为 0parent[0] = -1; // 该顶点没有父节点// 对于 V 个顶点的图,最需选择 V-1 条路径,即可构成最小生成树for (int x = 0; x < V - 1; x++){// 从 key 数组中找到权值最小的顶点所在的位置int u = min_Key(key, visited);// 该顶点划分到 A 类visited[u] = true;// 由于新顶点加入 A 类,因此需要更新 key 数组中的数据for (int v = 0; v < V; v++){// 如果类 B 中存在到下标为 u 的顶点的权值比 key 数组中记录的权值还小,表明新顶点的加入,使得类 B 到类 A 顶点的权值有了更好的选择if (cost[u][v] != 0 && visited[v] == false && cost[u][v] < key[v]){// 更新 parent 数组记录的各个顶点父节点的信息parent[v] = u;// 更新 key 数组key[v] = cost[u][v];}}}//根据 parent 记录的各个顶点父节点的信息,输出寻找到的最小生成树print_MST(parent, cost);}public static void main(String[] args) {int [][]cost = new int[V][V];System.out.println("输入图(顶点到顶点的路径和权值):");Scanner sc = new Scanner(System.in);while (true) {int p1 = sc.nextInt();int p2 = sc.nextInt();// System.out.println(p1+p2);if (p1 == -1 && p2 == -1) {break;}int wight = sc.nextInt();cost[p1-1][p2-1] = wight;cost[p2-1][p1-1] = wight;}// 根据用户输入的图的信息,寻找最小生成树find_MST(cost);}}
程序结果:
图 1 连通网中的顶点 A、B、C、D、S、T 分别用 1~6 的数字表示
23、克鲁斯卡尔算法
在连通网中查找最小生成树的常用方法有两个,分别称为普里姆算法和克鲁斯卡尔算法。本节,我们给您讲解克鲁斯卡尔算法。
克鲁斯卡尔算法查找最小生成树的方法是:将连通网中所有的边按照权值大小做升序排序,从权值最小的边开始选择,只要此边不和已选择的边一起构成环路,就可以选择它组成最小生成树。对于 N 个顶点的连通网,挑选出 N-1 条符合条件的边,这些边组成的生成树就是最小生成树。
举个例子,图 1 是一个连通网,克鲁斯卡尔算法查找图 1 对应的最小生成树,需要经历以下几个步骤: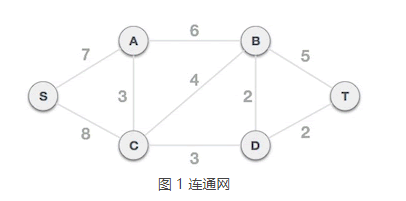
1) 将连通网中的所有边按照权值大小做升序排序:
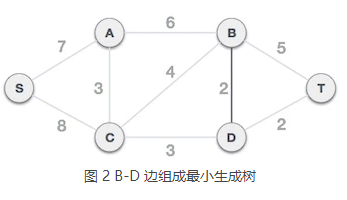
2) 从 B-D 边开始挑选,由于尚未选择任何边组成最小生成树,且 B-D 自身不会构成环路,所以 B-D 边可以组成最小生成树。
3) D-T 边不会和已选 B-D 边构成环路,可以组成最小生成树: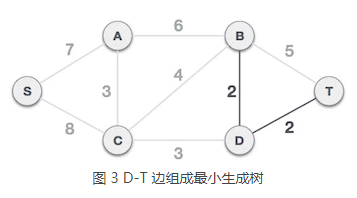
4) A-C 边不会和已选 B-D、D-T 边构成环路,可以组成最小生成树: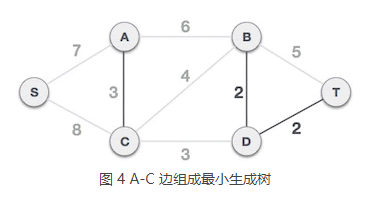
5) C-D 边不会和已选 A-C、B-D、D-T 边构成环路,可以组成最小生成树: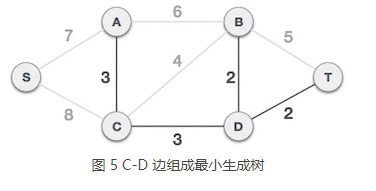
6) C-B 边会和已选 C-D、B-D 边构成环路,因此不能组成最小生成树: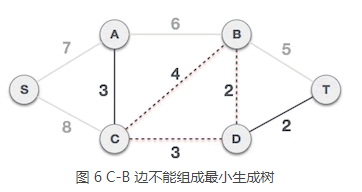
7) B-T 、A-B、S-A 三条边都会和已选 A-C、C-D、B-D、D-T 构成环路,都不能组成最小生成树。而 S-A 不会和已选边构成环路,可以组成最小生成树。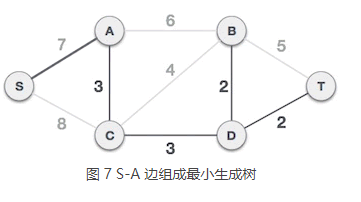
8) 如图 7 所示,对于一个包含 6 个顶点的连通网,我们已经选择了 5 条边,这些边组成的生成树就是最小生成树。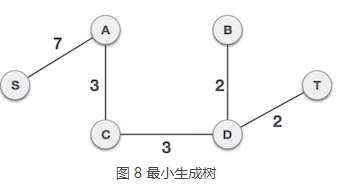
克鲁斯卡尔算法的具体实现
import java.util.Arrays;import java.util.Scanner;public class prim {static int N = 9; // 图中边的数量static int P = 6; // 图中顶点的数量//构建表示路径的类public static class edge implements Comparable<edge>{//每个路径都有 2 个顶点和 1 个权值int initial;int end;int weight;public edge(int initial, int end, int weight) {this.initial = initial;this.end = end;this.weight = weight;}//对每个 edge 对象根据权值做升序排序@Overridepublic int compareTo(edge o) {return this.weight - o.weight;}}public static void kruskal_MinTree(edge[] edges,edge [] minTree) {int []assists = new int[P];//每个顶点配置一个不同的标记值for (int i = 0; i < P; i++) {assists[i] = i;}//根据权值,对所有边进行升序排序Arrays.sort(edges);//遍历所有的边int num = 0;for (int i = 0; i < N; i++) {//找到当前边的两个顶点在 assists 数组中的位置下标int initial = edges[i].initial - 1;int end = edges[i].end - 1;//如果顶点位置存在且顶点的标记不同,说明不在一个集合中,不会产生回路if (assists[initial] != assists[end]) {//记录该边,作为最小生成树的组成部分minTree[num] = edges[i];//计数+1num++;int elem = assists[end];//将新加入生成树的顶点标记全不更改为一样的for (int k = 0; k < P; k++) {if (assists[k] == elem) {assists[k] = assists[initial];}}//如果选择的边的数量和顶点数相差1,证明最小生成树已经形成,退出循环if (num == P - 1) {break;}}}}public static void display(edge [] minTree) {System.out.println("最小生成树为:");int cost = 0;for (int i = 0; i < P - 1; i++) {System.out.println(minTree[i].initial+" - "+ minTree[i].end+" 权值为:"+minTree[i].weight);cost += minTree[i].weight;}System.out.print("总权值为:"+cost);}public static void main(String[] args) {Scanner scn = new Scanner(System.in);edge[] edges = new edge[N];edge[] minTree = new edge[P-1];System.out.println("请输入图中各个边的信息:");for(int i=0;i<N;i++) {int initial = scn.nextInt(), end = scn.nextInt(), weight = scn.nextInt();edges[i] = new edge(initial,end,weight);}kruskal_MinTree(edges,minTree);display(minTree);}}
程序结果:
将图 1 中的 A、B、C、D、S、T 顶点分别用数字 1~6 表示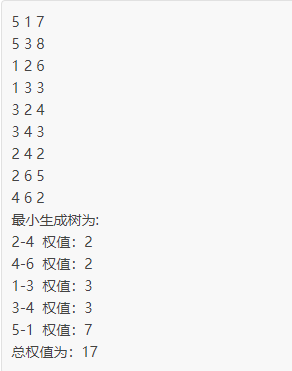
24、最短路径算法
在给定的图存储结构中,从某一顶点到另一个顶点所经过的多条边称为路径。
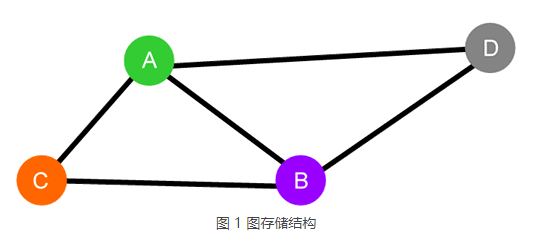
例如在图 1 所示的图结构中,从顶点 A 到 B 的路径有多条,包括 A-B、A-C-B 和 A-D-B。当我们给图中的每条边赋予相应的权值后,就可以从众多路径中找出总权值最小的一条,这条路径就称为最短路径。
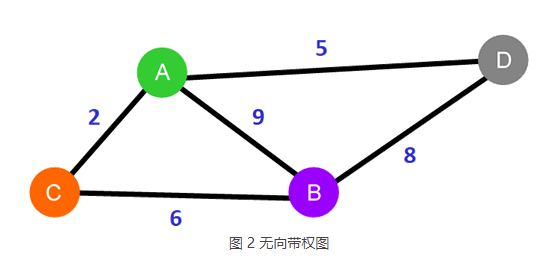
以图 2 为例,从顶点 A 到 B 的路径有 3 条,它们各自的总权值是:
A-B:9
A-C-B:2+6=8
A-D-B:5+8=13
经过对比,A-C-B 的总权值最小,它就是从顶点 A 到 B 的最短路径。
最短路径不仅适用于无向加权图,也适用于有向加权图,如下图所示: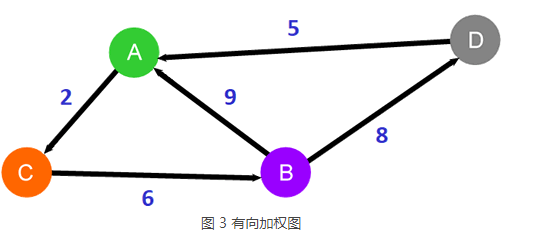
最短路径算法
| 最短路径算法 | 描 述 |
|---|---|
| 迪杰斯特拉算法 (Dijkstra) |
寻找某个特定顶点到其它所有顶点的最短路径,该算法要求所有路径的权值为非负数。 |
| 弗洛伊德算法( Floyd-Warshall) |
寻找各个顶点之间的最短路径,允许非环路的路径权值为负数,该算法不仅适用于稀疏图,在稠密图(路径数量多的图)中寻找最短路径的效率也很高。 |
| 贝尔曼福特算法(Bellman-Ford) | 寻找某个特定顶点到其它所有顶点的最短路径,该算法允许路径的权值为负数。 |
推荐阅读:
- 图解贝尔曼福特算法:详尽的讲解过程和丰富的实例演示,最终用 Java 语言实现该算法。
|
| 约翰逊算法(Johnson) | 寻找各个顶点之间的最短路径,允许非环路的路径权值为负数,该算法更适用于稀疏图(路径数量少的图)。
推荐阅读:
- Johnson 全源最短路径算法:详细讲解了 Johnson 算法的实现过程,最终实现的演示代码用 C# 实现。
- Johnson 全源最短路径算法:以作者自身的理解讲解了 Johnson 算法,最终实现的演示程序用 C++ 实现。
|
25、迪杰斯特拉算法
迪杰斯特拉算法用于查找图中某个顶点到其它所有顶点的最短路径,该算法既适用于无向加权图,也适用于有向加权图。
注意,使用迪杰斯特拉算法查找最短路径时,必须保证图中所有边的权值为非负数,否则查找过程很容易出错。
实现思路:
图 1 是一个无向加权图,我们就以此图为例,给大家讲解迪杰斯特拉算法的实现思路。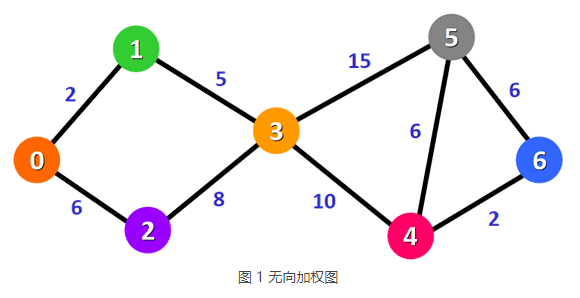
假设用迪杰斯特拉算法查找从顶点 0 到其它顶点的最短路径,具体过程是:
1) 统计从顶点 0 直达其它顶点的权值,如下表所示:
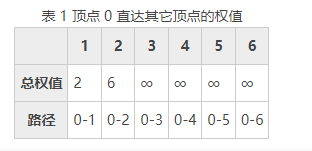
∞ 表示两个顶点之间无法直达,对应的权值为无穷大。
2) 表 1 中,权值最小的是 0-1 路径,它也是从顶点 0 到顶点 1 的最短路径(如图 2 所示)。原因很简单,从顶点 0 出发一共只有 0-1 和 0-2 两条路径,0-2 的权值本就比 0-1 大,所以从 0-2 出发不可能找得到比 0-1 权值更小的路径。
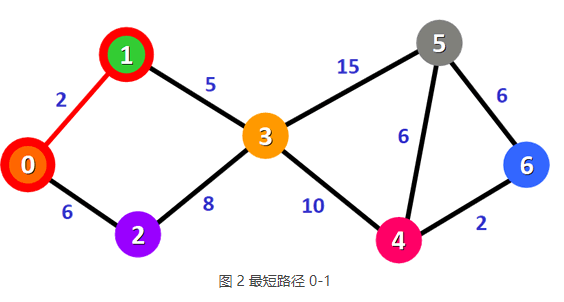
3) 找到最短路径 0-1 后,沿 0-1 路径方向查找更短的到达其它顶点的路径,并对表 1 进行更新。
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 总权值 | 2 | 6 | 2+5 | ∞ | ∞ | ∞ |
| 路径 | 0-1 | 0-2 | 0-1-3 | 0-4 | 0-5 | 0-6 |
绿色加粗的权值是已确认为最短路径的权值,后续选择总权值最小的路径时不再重复选择;红色加粗的权值为刚刚更新的权值。
更新后的表格如表 2 所示,沿 0-1 路径可以到达顶点 3,且 0-1-3 的总权值比 0-3 更小。表 2 中,总权值最小的路径是 0-2,它也是从顶点 0 到顶点 2 的最短路径,如下图所示。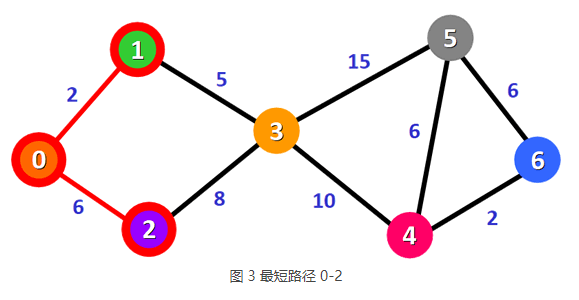
4) 重复之前的操作,沿 0-2 路径方向查找更短的到达其它顶点的路径。遗憾地是,从顶点 2 只能到达顶点 3,且 0-2-3 的总权值比表 2 中记录的 0-1-3 更大,因此表 2 中记录的数据维持不变。
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 总权值 | 2 | 6 | 7 | ∞ | ∞ | ∞ |
| 路径 | 0-1 | 0-2 | 0-1-3 | 0-4 | 0-5 | 0-6 |
5) 表 3 中,总权值最小的是 0-1-3,它也是顶点 0 到顶点 3 的最短路径。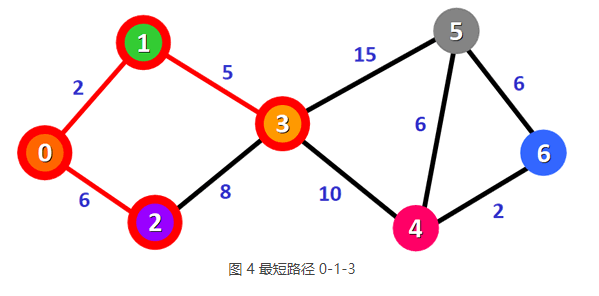
沿 0-1-3 路径方向,查找到其它顶点更短的路径并更新表 3。更新后的表格为:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 总权值 | 2 | 6 | 7 | 7+10 | 7+15 | ∞ |
| 路径 | 0-1 | 0-2 | 0-1-3 | 0-1-3-4 | 0-1-3-5 | 0-6 |
6) 表 4 中,总权值最小的是 0-1-3-4,它是顶点 0 到顶点 4 的最短路径。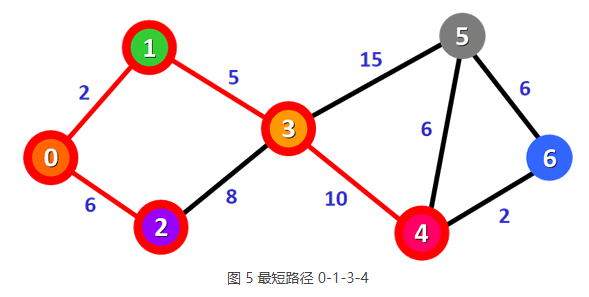
从顶点 4 出发,查找顶点 0 到其它顶点更短的路径并更新表 4。更新后的表格为:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 总权值 | 2 | 6 | 7 | 17 | 22 | 17+2 |
| 路径 | 0-1 | 0-2 | 0-1-3 | 0-1-3-4 | 0-1-3-5 | 0-1-3-4-6 |
7) 表 5 中,总权值最小的路径是 0-1-3-4-6,它是顶点 0 到顶点 6 的最短路径。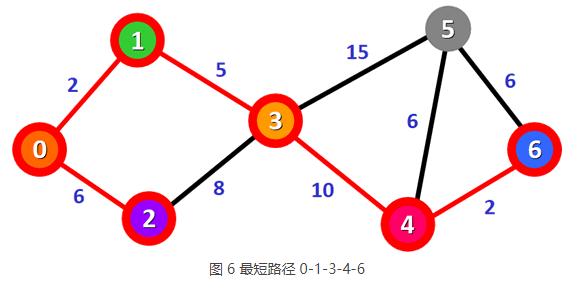
8) 从图 6 可以看到,只剩下顶点 0 到顶点 5 的最短路径尚未确定。从顶点 6 出发到达顶点 5 的路径是 0-1-3-4-6-5,对应的总权值为 25,大于表 5 中记录的 0-1-3-5 路径,因此 0-1-3-5 是顶点 0 到顶点 5 的最短路径。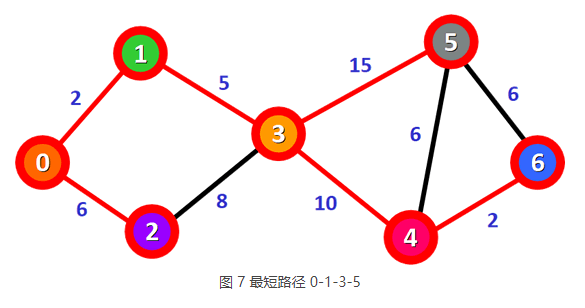
由此借助迪杰斯特拉算法,我们找出了顶点 0 到其它所有顶点的最短路径,如下表所示:
| 1 | 2 | 3 | 4 | 5 | 6 | |
|---|---|---|---|---|---|---|
| 总权值 | 2 | 6 | 7 | 17 | 22 | 19 |
| 路径 | 0-1 | 0-2 | 0-1-3 | 0-1-3-4 | 0-1-3-5 | 0-1-3-4-6 |
代码实现:
import java.util.Scanner;public class Dijkstra {static int V = 9; // 图中边的数量public static class MGraph {int[] vexs = new int[V]; // 存储图中顶点数据int[][] arcs = new int[V][V]; // 二维数组,记录顶点之间的关系int vexnum, arcnum; // 记录图的顶点数和弧(边)数}public static int LocateVex(MGraph G, int V) {int i = 0;// 遍历一维数组,找到变量vfor (; i < G.vexnum; i++) {if (G.vexs[i] == V) {break;}}// 如果找不到,输出提示语句,返回-1if (i > G.vexnum) {System.out.println("顶点输入有误");return -1;}return i;}// 构造无向有权图public static void CreatDG(MGraph G) {Scanner scn = new Scanner(System.in);System.out.print("输入图的顶点数和边数:");G.vexnum = scn.nextInt();G.arcnum = scn.nextInt();System.out.print("输入各个顶点:");for (int i = 0; i < G.vexnum; i++) {G.vexs[i] = scn.nextInt();}for (int i = 0; i < G.vexnum; i++) {for (int j = 0; j < G.vexnum; j++) {G.arcs[i][j] = 65535;}}System.out.println("输入各个边的数据:");for (int i = 0; i < G.arcnum; i++) {int v1 = scn.nextInt();int v2 = scn.nextInt();int w = scn.nextInt();int n = LocateVex(G, v1);int m = LocateVex(G, v2);if (m == -1 || n == -1) {return;}G.arcs[n][m] = w;G.arcs[m][n] = w;}}// 迪杰斯特拉算法,v0表示有向网中起始点所在数组中的下标public static void Dijkstra_minTree(MGraph G, int v0, int[] p, int[] D) {int[] tab = new int[V]; // 为各个顶点配置一个标记值,用于确认该顶点是否已经找到最短路径// 对各数组进行初始化for (int v = 0; v < G.vexnum; v++) {tab[v] = 0;D[v] = G.arcs[v0][v];p[v] = 0;}// 由于以v0位下标的顶点为起始点,所以不用再判断D[v0] = 0;tab[v0] = 1;int k = 0;for (int i = 0; i < G.vexnum; i++) {int min = 65535;// 选择到各顶点权值最小的顶点,即为本次能确定最短路径的顶点for (int w = 0; w < G.vexnum; w++) {if (tab[w] != 1) {if (D[w] < min) {k = w;min = D[w];}}}// 设置该顶点的标志位为1,避免下次重复判断tab[k] = 1;// 对v0到各顶点的权值进行更新for (int w = 0; w < G.vexnum; w++) {if (tab[w] != 1 && (min + G.arcs[k][w] < D[w])) {D[w] = min + G.arcs[k][w];p[w] = k;// 记录各个最短路径上存在的顶点}}}}public static void main(String[] args) {MGraph G = new MGraph();CreatDG(G);int[] P = new int[V]; // 记录顶点 0 到各个顶点的最短的路径int[] D = new int[V]; // 记录顶点 0 到各个顶点的总权值Dijkstra_minTree(G, 0, P, D);System.out.println("最短路径为:");for (int i = 1; i < G.vexnum; i++) {System.out.print(i + " - " + 0 + " 的最短路径中的顶点有:");System.out.print(i + "-");int j = i;// 由于每一段最短路径上都记录着经过的顶点,所以采用嵌套的方式输出即可得到各个最短路径上的所有顶点while (P[j] != 0) {System.out.print(P[j] + "-");j = P[j];}System.out.println("0");}System.out.println("源点到各顶点的最短路径长度为:");for (int i = 1; i < G.vexnum; i++) {System.out.println(G.vexs[0] + " - " + G.vexs[i] + " : " + D[i]);}}}
程序结果:
26、弗洛伊德算法
在一个加权图中,如果想找到各个顶点之间的最短路径,可以考虑使用弗洛伊德算法。
弗洛伊德算法既适用于无向加权图,也适用于有向加权图。使用弗洛伊德算法查找最短路径时,只允许环路的权值为负数,其它路径的权值必须为非负数,否则算法执行过程会出错。
实现思路
弗洛伊德算法是基于动态规划算法实现的,接下来我们以在图 1 所示的有向加权图中查找各个顶点之间的最短路径为例,讲解弗洛伊德算法的实现思路。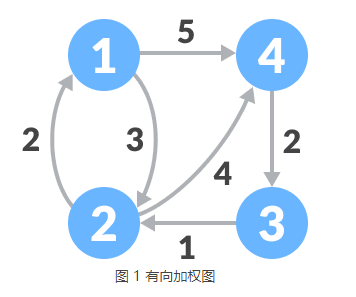
图 1 中不存在环路,且所有路径(边)的权值都为正数,因此可以使用弗洛伊德算法。
弗洛伊德算法查找图 1 中各个顶点之间的最短路径,实现过程如下:
1) 建立一张表格,记录每个顶点直达其它所有顶点的权值:
| 目标顶点 | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 起始顶点 | 1 | 0 | 3 | ∞ | 5 |
| 2 | 2 | 0 | ∞ | 4 | |
| 3 | ∞ | 1 | 0 | ∞ | |
| 4 | ∞ | ∞ | 2 | 0 |
起始顶点指的是从哪个顶点出发,目标顶点指的是要达到的顶点,例如 2->1 路径的权值是 2,顶点 2 是起始顶点,顶点 1 是目标顶点。此外,∞ 表示无穷大的数,即顶点之间不存在直达的路径。
2) 在表 1 的基础上,将顶点 1 作为 “中间顶点”,计算从各个顶点出发途径顶点 1 再到达其它顶点的权值,如果比表 1 中记录的权值更小,证明两个顶点之间存在更短的路径,对表 1 进行更新。
从各个顶点出发,途径顶点 1 再到达其它顶点的路径以及对应的权值分别是:
- 2-1-3:权值为 2 + ∞ = ∞,表 1 中记录的 2-3 的权值也是 ∞;
- 2-1-4:权值为 2 + 5 = 7,表 1 中记录的 2-4 的权值是 4;
- 3-1-2:权值为 ∞ + 3,表 1 中记录的 3-2 的权值是 1;
- 3-1-4:权值为 ∞ + 5,表 1 中记录的 3-4 的权值是 ∞;
- 4-1-2:权值为 ∞ + 3,表 1 中记录的 4-2 的权值是 ∞;
- 4-1-3:权值为 ∞ + ∞,表 1 中记录的 4-3 的权值是 2。
以上所有的路径中,没有比表 1 中记录的权值最小的路径,所以不需要对表 1 进行更新。
3) 在表 1 的基础上,以顶点 2 作为 “中间顶点”,计算从各个顶点出发途径顶点 2 再到达其它顶点的权值:
- 1-2-3:权值为 3 + ∞,表 1 中记录的 1-3 的权值为 ∞;
- 1-2-4:权值为 3 + 4 = 7,表 1 中 1-4 的权值为 5;
- 3-2-1:权值为 1 + 2 = 3,表 1 中 3-1 的权值为 ∞,3 < ∞;
- 3-2-4:权值为 1 + 4 = 5,表 1 中 3-4 的权值为 ∞,5 < ∞;
- 4-2-1:权值为 ∞ + 2,表 1 中 4-1 的权值为 ∞;
- 4-2-3:权值为 ∞ + ∞,表 1 中 4-3 的权值为 2。
以顶点 2 作为 “中间顶点”,我们找到了比 3-1、3-4 更短的路径,对表 1 进行更新:
| 目标顶点 | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 起始顶点 | 1 | 0 | 3 | ∞ | 5 |
| 2 | 2 | 0 | ∞ | 4 | |
| 3 | 3(3-2-1) | 1 | 0 | 5(3-2-4) | |
| 4 | ∞ | ∞ | 2 | 0 |
4) 在表 2 的基础上,将顶点 3 作为 “中间顶点”,计算从各个顶点出发途径顶点 3 再到达其它顶点的权值:
- 1-3-2 权值为 ∞ + 1,表 2 中 1-2 的权值为 3;
- 1-3-4 权值为 ∞ + 5,表 2 中 1-4 的权值为 5;
- 2-3-1 权值为 ∞ + 3,表 2 中 2-1 的权值为 2;
- 2-3-4 权值为 ∞ + 5,表 2 中 2-4 的权值为 4;
- 4-3-1 权值为 2 + 3 = 5,表 2 中 4-1 的权值为 ∞,5 < ∞;
- 4-3-2 权值为 2 + 1 = 3,表 2 中 4-2 的权值为 ∞,3 < ∞;
以顶点 3 作为 “中间顶点”,我们找到了比 4-1、4-2 更短的路径,对表 2 进行更新:
| 目标顶点 | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 起始顶点 | 1 | 0 | 3 | ∞ | 5 |
| 2 | 2 | 0 | ∞ | 4 | |
| 3 | 3(3-2-1) | 1 | 0 | 5(3-2-4) | |
| 4 | 5(4-3-2-1) | 3(4-3-2) | 2 | 0 |
5) 在表 3 的基础上,将顶点 4 作为 “中间顶点”,计算从各个顶点出发途径顶点 4 再到达其它顶点的权值:
- 1-4-2 权值为 5 + 3 = 8,表 3 中 1-2 的权值为 3;
- 1-4-3 权值为 5 + 2 = 7,表 3 中 1-3 的权值为 ∞,7 < ∞;
- 2-4-1 权值为 4 + 5 = 9,表 3 中 2-1 的权值为 2;
- 2-4-3 权值为 4 + 2 = 6,表 3 中 2-3 的权值为 ∞,6 < ∞;
- 3-4-1 权值为 4 + 5 = 9,表 3 中 3-1 的权值为 3;
- 3-4-2 权值为 5 + 5 = 10 ,表 3 中 3-2 的权值为 1。
以顶点 4 作为 “中间顶点”,我们找到了比 1-3、2-3 更短的路径,对表 3 进行更新:
| 目标顶点 | |||||
|---|---|---|---|---|---|
| 1 | 2 | 3 | 4 | ||
| 起始顶点 | 1 | 0 | 3 | 7(1-4-3) | 5 |
| 2 | 2 | 0 | 6(2-4-3) | 4 | |
| 3 | 3(3-2-1) | 1 | 0 | 5(3-2-4) | |
| 4 | 5(4-3-2-1) | 3(4-3-2) | 2 | 0 |
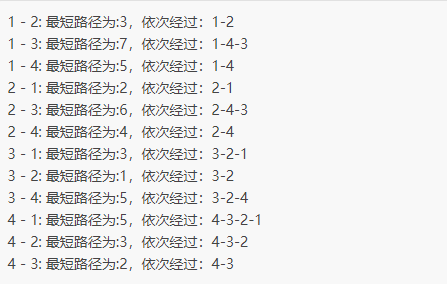
通过将所有的顶点分别作为“中间顶点”,最终得到的表 4 就记录了各个顶点之间的最短路径。例如,4-1 的最短路径为 4-3-2-1。
具体实现
public class Floyd {static int V = 4; // 顶点的个数static int[][] P = new int[V][V]; // 记录各个顶点之间的最短路径static int INF = 65535; // 设置一个最大值// 中序递归输出各个顶点之间最短路径的具体线路public static void printPath(int i, int j) {int k = P[i][j];if (k == 0)return;printPath(i, k);System.out.print((k + 1) + "-");printPath(k, j);}// 输出各个顶点之间的最短路径public static void printMatrix(int[][] graph) {for (int i = 0; i < V; i++) {for (int j = 0; j < V; j++) {if (j == i) {continue;}System.out.print((i + 1) + " - " + (j + 1) + ":最短路径为:");if (graph[i][j] == INF)System.out.println("INF");else {System.out.print(graph[i][j]);System.out.print(",依次经过:" + (i + 1) + "-");// 调用递归函数printPath(i, j);System.out.println((j + 1));}}}}// 实现弗洛伊德算法,graph[][V] 为有向加权图public static void floydWarshall(int[][] graph) {int i, j, k;// 遍历每个顶点,将其作为其它顶点之间的中间顶点,更新 graph 数组for (k = 0; k < V; k++) {for (i = 0; i < V; i++) {for (j = 0; j < V; j++) {// 如果新的路径比之前记录的更短,则更新 graph 数组if (graph[i][k] + graph[k][j] < graph[i][j]) {graph[i][j] = graph[i][k] + graph[k][j];// 记录此路径P[i][j] = k;}}}}// 输出各个顶点之间的最短路径printMatrix(graph);}public static void main(String[] args) {// 有向加权图中各个顶点之间的路径信息int[][] graph = new int[][] { { 0, 3, INF, 5 }, { 2, 0, INF, 4 }, { INF, 1, 0, INF }, { INF, INF, 2, 0 } };floydWarshall(graph);}}
程序结果: