1、数组的最大值和最小值

1.1、普通方法

普通算法的解决思路是：创建两个变量 max 和 min 分别记录数组中的最大值和最小值，它们的初始值都是数组中的第一个数字。从第 2 个数字开始遍历数组，每遇到一个比 max 大的数字，就将它存储到 max 变量中；每遇到一个比 min 小的数字，就将它存储到 min 变量中。直到遍历完整个数组，max 记录的就是数组中的最大值，min 记录的就是数组中的最小值。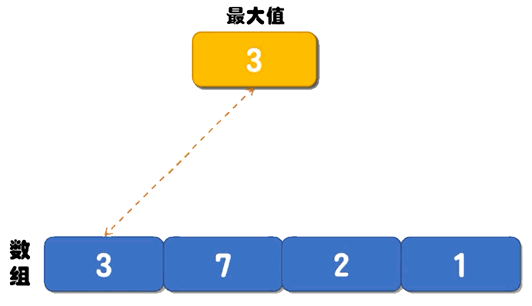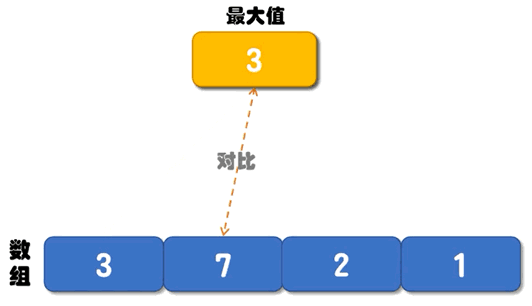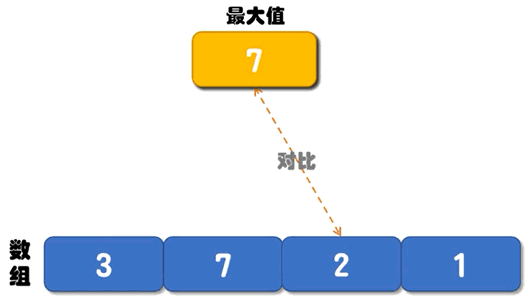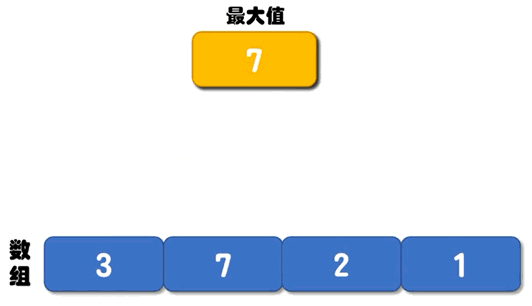
2-210R0100614128.gif

1.2、分治算法解决

下图展示了用分治算法查找 {3, 7, 2, 1} 中最大值的实现过程：

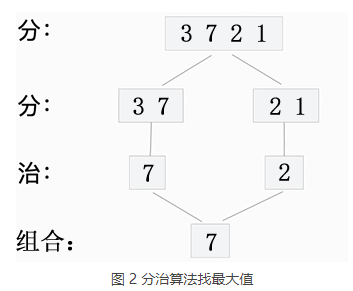
image.png

分治算法的实现思路是：不断地等分数组中的元素，直至各个分组中元素的个数 ≤2。由于每个分组内的元素最多有 2 个，很容易就可以找出其中的最值（最大值或最小值），然后这些最值再进行两两比较，最终找到的最值就是整个数组中的最值。

代码实现：

  1. public class Demo {
  2.     public static int get_max(int [] arr,int left,int right) {
  3.         //如果数组不存在或者数组内没有元素
  4.         if (arr == null || arr.length == 0) {
  5.             return -1;
  6.         }
  7.         //如果查找范围中仅有 2 个数字，则直接比较即可
  8.         if(right - left <=1) {
  9.             if(arr[left] >= arr[right]) {
  10.                 return arr[left];
  11.             }
  12.             return arr[right];
  13.         }
  14.         //等量划分成 2 个区域
  15.         int middle = (right-left)/2 + left;
  16.         int max_left = get_max(arr,left,middle);
  17.         int max_right = get_max(arr,middle+1,right);
  18.         if(max_left >= max_right) {
  19.             return max_left;
  20.         }else {
  21.             return max_right;
  22.         }
  23.     }
  24.     public static void main(String[] args) {
  25.         int [] arr = new int[] { 3,7,2,1 };
  26.         int max = get_max(arr,0,3);
  27.         System.out.println("最大值："+max);
  28.     }
  29. }

程序结果:
image.png

2、汉诺塔问题

汉诺塔问题源自印度一个古老的传说，印度教的“创造之神”梵天创造世界时做了 3 根金刚石柱，其中的一根柱子上按照从小到大的顺序摞着 64 个黄金圆盘。梵天命令一个叫婆罗门的门徒将所有的圆盘移动到另一个柱子上，移动过程中必须遵守以下规则：

  • 每次只能移动柱子最顶端的一个圆盘；
  • 每个柱子上，小圆盘永远要位于大圆盘之上；


图 1 给您展示了包含 3 个圆盘的汉诺塔问题：

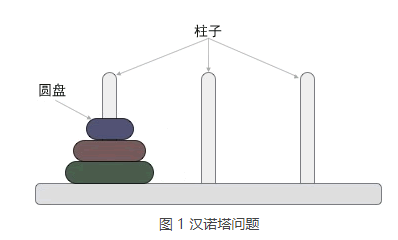
image.png

一根柱子上摞着 3 个不同大小的圆盘，那么在不违反规则的前提下，如何将它们移动到另一个柱子上呢？图 2 给大家提供了一种实现方案：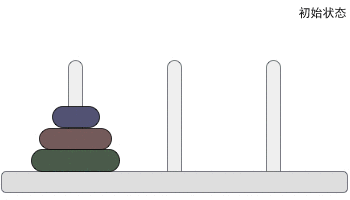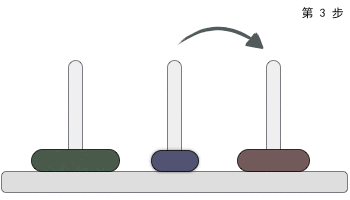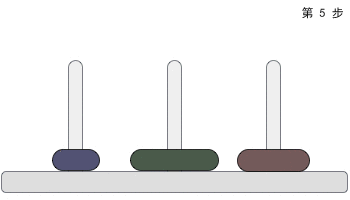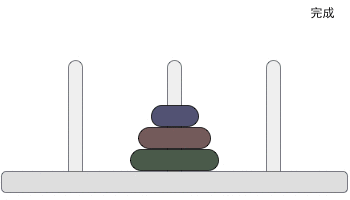
2-210R0100929200.gif
图 2 汉诺塔问题的解决方案

汉诺塔问题中，3 个圆盘至少需要移动 7 次，移动 n 的圆盘至少需要操作 2n-1 次。
在汉诺塔问题中，当圆盘个数不大于 3 时，多数人都可以轻松想到移动方案，随着圆盘数量的增多，汉诺塔问题会越来越难。也就是说，圆盘的个数直接决定了汉诺塔问题的难度，解决这样的问题可以尝试用分治算法，将移动多个圆盘的问题分解成多个移动少量圆盘的小问题，这些小问题很容易解决，从而可以找到整个问题的解决方案。

分治算法解决汉诺塔问题
为了方便讲解，我们将 3 个柱子分别命名为起始柱、目标柱和辅助柱。实际上，解决汉诺塔问题是有规律可循的：
1) 当起始柱上只有 1 个圆盘时，我们可以很轻易地将它移动到目标柱上；

2) 当起始柱上有 2 个圆盘时，移动过程如下图所示：

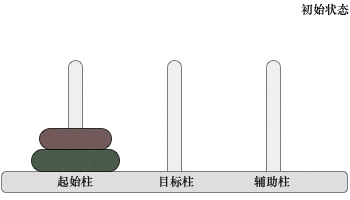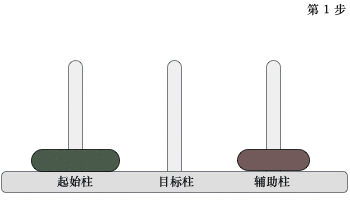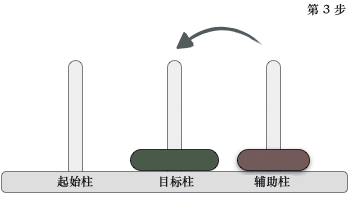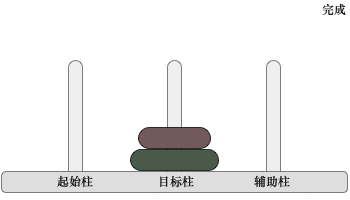
2-210R01009515I.gif
图 3 移动两个圆盘

移动过程是：先将起始柱上的 1 个圆盘移动到辅助柱上，然后将起始柱上遗留的圆盘移动到目标柱上，最后将辅助柱上的圆盘移动到目标柱上。

3) 当起始柱上有 3 个圆盘时，移动过程如图 2 所示，仔细观察会发现，移动过程和 2 个圆盘的情况类似：先将起始柱上的 2 个圆盘移动到辅助柱上，然后将起始柱上遗留的圆盘移动到目标柱上，最后将辅助柱上的圆盘移动到目标柱上。

通过分析以上 3 种情况的移动思路，可以总结出一个规律：对于 n 个圆盘的汉诺塔问题，移动圆盘的过程是：

  1. 将起始柱上的 n-1 个圆盘移动到辅助柱上；
  2. 将起始柱上遗留的 1 个圆盘移动到目标柱上；
  3. 将辅助柱上的所有圆盘移动到目标柱上。


由此，n 个圆盘的汉诺塔问题就简化成了 n-1 个圆盘的汉诺塔问题。按照同样的思路，n-1 个圆盘的汉诺塔问题还可以继续简化，直至简化为移动 3 个甚至更少圆盘的汉诺塔问题。

代码实现:

  1. public class Demo {
  2.     // 统计移动次数
  3.     public static int i = 1;
  5.     public static void hanoi(int num, char sou, char tar, char sux) {
  6.         // 如果圆盘数量仅有 1 个，则直接从起始柱移动到目标柱
  7.         if (num == 1) {
  8.             System.out.println("第" + i + "次:从" + sou + "移动到" + tar);
  9.             i++;
  10.         } else {
  11.             // 递归调用 hanoi() 函数，将 num-1 个圆盘从起始柱移动到辅助柱上
  12.             hanoi(num - 1, sou, sux, tar);
  13.             // 将起始柱上剩余的最后一个大圆盘移动到目标柱上
  14.             System.out.println("第" + i + "次:从" + sou + "移动到" + tar);
  15.             i++;
  16.             // 递归调用 hanoi() 函数，将辅助柱上的 num-1 圆盘移动到目标柱上
  17.             hanoi(num - 1, sux, tar, sou);
  18.         }
  19.     }
  21.     public static void main(String[] args) {
  22.         // 以移动 3 个圆盘为例，起始柱、目标柱、辅助柱分别用 A、B、C 表示
  23.         hanoi(3, 'A', 'B', 'C');
  24.     }
  25. }

执行结果:
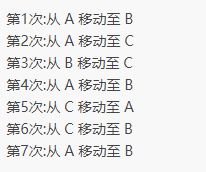
image.png

3、部分背包问题

在限定条件下，如何从众多物品中选出收益最高的几件物品，这样的问题就称为背包问题。

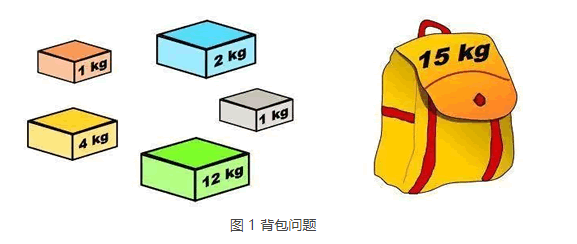
image.png

举个简单的例子，商店的货架上摆放着不同重量和价值的商品，一个小偷在商店行窃，他携带的背包只能装固定重量的商品，选择哪些商品才能获得最大的收益呢？这个问题就属于背包问题，限定条件是背包的承重，最终目标是令背包中存放的物品的总收益最高。

根据不同的限定条件，背包问题还可以有更细致的划分：

  • 0-1 背包问题：每件物品都不可再分，要么整个装入背包，要么放弃，不允许出现类似“将物品的 1/3 装入背包”的情况；
  • 部分背包问题：每件物品是可再分的，即允许将某件物品的一部分（例如 1/3）放入背包；
  • 完全背包问题：挑选物品时，每件物品可以选择多个，也就是说不限物品的数量。
  • 多重背包问题：每件物品的数量是有严格规定的，比如物品 A 有 2 件，物品 B 有 3 件。


不同的背包问题，对应的解决方案也不相同。本节我们给大家讲解，如何用贪心算法解决部分背包问题。

3.1、贪心算法解决部分背包问题

假设商店中有 3 种商品，它们各自的重量和收益是：

  • 商品 1：重量 10 斤，收益 60 元；
  • 商品 2：重量 20 斤，收益 100 元；
  • 商品 3：重量 30 斤，收益 120 元。


对于每件商品，顾客可以购买商品的一部分（可再分）。一个小偷想到商店行窃，他的背包最多只能装 50 斤的商品，如何选择才能获得最大的收益呢？
贪心算法解决此问题的思路是：计算每个商品的收益率（收益/重量），优先选择收益率最大的商品，直至所选商品的总重量达到 50 斤。

代码实现:

  1. public class Demo {
  2.     //根据收益率，对记录的商品进行从大到小排序
  3.     public static void sort(float [] w, float [] p) {
  4.         int length = w.length;
  5.         //用v[]存商品的收益率
  6.         float [] v = new float[length];
  7.         for (int i=0;i<length;i++) {
  8.             v[i] = p[i]/w[i];
  9.         }
  10.         //根据 v 数组记录的各个商品收益率的大小，同时对 w 和 p 数组进行排序
  11.         for (int i = 0; i < length; i++) {
  12.             for (int j = i + 1; j < length; j++) {
  13.                 if (v[i] < v[j]) {
  14.                     float temp = v[i];
  15.                     v[i] = v[j];
  16.                     v[j] = temp;
  17.                     temp = w[i];
  18.                     w[i] = w[j];
  19.                     w[j] = temp;
  20.                     temp = p[i];
  21.                     p[i] = p[j];
  22.                     p[j] = temp;
  23.                 }
  24.             }
  25.         }
  26.     }
  27.     /*贪心算法解决部分背包问题
  28.     w：记录各个商品的总重量
  29.     p：记录各个商品的总价值
  30.     result：记录各个商品装入背包的比例
  31.     W：背包的容量
  32.     */
  33.     public static void fractional_knapsack(float []w, float []p, float []result, float W) {
  34.         //根据收益率，重新对商品进行排序
  35.         sort(w, p);
  36.         int i=0;
  37.         //从收益率最高的商品开始装入背包，直至背包装满为止
  38.         while (W > 0) {
  39.             float temp = W > w[i]?w[i]:W;
  40.             result[i] = temp / w[i];
  41.             W -= temp;
  42.             i++;
  43.         }
  44.     }
  45.     public static void main(String[] args) {
  46.         //设定背包的容量
  47.         float W = 50;
  48.         //各个商品的重量
  49.         float [] w = { 10,30,20 };
  50.         //各个商品的价值
  51.         float [] p = { 60,100,120 };
  52.         //统计背包中商品的总收益
  53.         float [] result = {0,0,0};
  54.         //调用解决部分背包问题的函数
  55.         fractional_knapsack(w,p,result,W);
  56.         //统计背包中商品的总收益
  57.         float values = 0;
  58.         //根据 result 数组中记录的数据，决定装入哪些商品
  59.         for (int i = 0; i < w.length; i++) {
  60.             if (result[i] == 1) {
  61.                 System.out.println("总重量为"+w[i]+",总价值为"+p[i]+"的商品全部装入");
  62.                 values += p[i];
  63.             }
  64.             else if (result[i] == 0)
  65.                 System.out.println("总重量为"+w[i]+",总价值为"+p[i]+"的商品不装");
  66.             else {
  67.                 System.out.println("总重量为"+w[i]+",总价值为"+p[i]+"的商品装入"+result[i]*100+"%");
  68.                 values += p[i] * result[i];
  69.             }
  70.         }
  71.         System.out.print("最终收获的商品价值为"+values);
  72.     }
  73. }

程序结果:
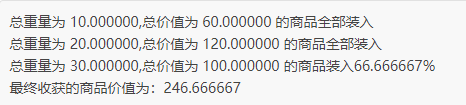
image.png
当背包最大承重为 50 斤时，商品一全部装入，商品二也全部装入，商品三装入 2/3，此时收益是最大的。

4、背包问题

商店的货架上摆放着不同重量和价值的商品，一个小偷在商店行窃，他携带的背包只能装固定重量的商品。装哪些商品才能获得最大的收益呢？在限定条件内找到最佳的物品组合，这样的问题统称为背包问题。

根据限定的条件不同，背包问题还可以细分：

  • 部分背包问题：所有物品是可再分的，即允许将某件物品的一部分（例如 1/3）放入背包；
  • 0-1 背包问题：所有物品不可再分，要么整个装入背包，要么放弃，不允许出现“仅选择物品的 1/3 装入背包”的情况；
  • 完全背包问题：不对每一件物品的数量做限制，同一件物品可以选择多个装入背包；
  • 多重背包问题：每件物品的数量是有严格规定的，比如物品 A 有 2 件，物品 B 有 3 件。


前面章节中，我们学会了用贪心算法解决部分背包问题。本节，我们学习如何用动态规划算法解决 0-1 背包问题。

动态规划解决01背包问题
虚拟一个场景，商店中拥有 5 件商品，它们各自的重量和收益分别是：

  • 商品 1：重量 1 斤，收益 1 元；
  • 商品 2：重量 2 斤，收益 6 元；
  • 商品 3：重量 5 斤，收益 18 元；
  • 商品 4：重量 6 斤，收益 22 元；
  • 商品 5：重量 7 斤，收益 28 元。


所有商品不可再分，顾客要么“整件”购买商品，要么放弃购买。一个小偷想窃取商品，他的背包只能装 11 斤商品，如何选择商品才能获得最大的收益呢？

动态规划算法解决此问题的核心思想是：背包承重 1 斤时所能获得的最大收益是很容易计算的，在此基础上，可以推算出背包承重 2 斤、3斤、…、14斤、15斤时所能获得的最大收益。建立如下这张表格，依次将各个商品装入不同承重的背包中，计算出它们所能获得的最大收益。

商品种类 背包承重
0 1 2 3 4 5 6 7 8 9 10 11
不装任何商品 0 0 0 0 0 0 0 0 0 0 0 0
w1 = 1，v1 = 1
w2 = 2，v2 = 6
w3 = 5，v3 = 18
w4 = 6，v4 = 22
w5 = 7，v5 = 28

表格中，wi 表示第 i 件商品的重量，vi 表示第 i 件商品的收益值。承重不同的各个背包尚未装入商品时，对应的收益值都为 0。
1) 首先考虑将商品一装入各个背包，除了承重值为 0 的背包，其它背包都能装入，且与不装任何商品相比，装入商品一后各个背包的收益更大，各个背包的收益值如表 2 所示：

商品种类 背包承重
0 1 2 3 4 5 6 7 8 9 10 11
不装任何商品 0 0 0 0 0 0 0 0 0 0 0 0
w1 = 1，v1 = 1 0 1 1 1 1 1 1 1 1 1 1 1
w2 = 2，v2 = 6
w3 = 5，v3 = 18
w4 = 6，v4 = 22
w5 = 7，v5 = 28


我们用 f(n) 表示承重值为 n 的背包对应的最大收益。从算法的角度，各个背包收益值是这样计算的：f(1)=1+f(0)、f(2)=1+f(1)、…、f(11)=1+f(10)，其中等号右侧表达式中的 1 指的是商品一的收益值，f(0)~f(10) 指的是不装任何商品时承重分别为 0~10 的背包对应的收益值，借助表格可以看到，它们的值都为 0。

2) 考虑将商品二装入各个背包，除了承重值为 0 和 1 的背包，其它背包都可以装入。我们可以计算出它们各自对应的收益值：
f(2) = 6 + f(0) = 1
f(3) = 6 + f(1) = 6
f(4) = 6 + f(2) = 7
…
f(9) = 6 + f(7) = 7
f(10) = 6 + f(8) = 7
f(11) = 6 + f(9) = 7
等号右侧 f(0)~f(9) 的值是表 2 中装入商品一的各个背包对应的收益值。相比装入商品一统计的各个背包的收益值，装入商品二能使提高各个背包的收益。更新后的表格为：

商品种类 背包承重
0 1 2 3 4 5 6 7 8 9 10 11
不装任何商品 0 0 0 0 0 0 0 0 0 0 0 0
w1 = 1，v1 = 1 0 1 1 1 1 1 1 1 1 1 1 1
w2 = 2，v2 = 6 0 1 6 7 7 7 7 7 7 7 7 7
w3 = 5，v3 = 18
w4 = 6，v4 = 22
w5 = 7，v5 = 28


3) 考虑将商品三装入各个背包，除了承重值为小于 5 的背包，其它背包都可以装入。我们可以计算出它们各自对应的收益值：
f(5) = 18 + f(0) = 18
f(6) = 18 + f(1) = 19
f(7) = 18 + f(2) = 24
f(8) = 18 + f(3) = 25
f(9) = 18 + f(4) = 25
f(10) = 18 + f(5) = 25
f(11) = 18 + f(6) = 25
等号右侧 f(0)~f(6) 的值是表 2 中装入商品二的各个背包对应的收益值。和装入商品二时统计的各个背包的收益值相比，装入商品三能提高各个背包的收益。更新后的表格为：

商品种类 背包承重
0 1 2 3 4 5 6 7 8 9 10 11
不装任何商品 0 0 0 0 0 0 0 0 0 0 0 0
w1 = 1，v1 = 1 0 1 1 1 1 1 1 1 1 1 1 1
w2 = 2，v2 = 6 0 1 6 7 7 7 7 7 7 7 7 7
w3 = 5，v3 = 18 0 1 6 7 7 18 19 24 25 25 25 25
w4 = 6，v4 = 22
w5 = 7，v5 = 28


4) 采用同样的方法，我们可以将表 4 中缺失的数据补全，最终得到的表格为：

商品种类 背包承重
0 1 2 3 4 5 6 7 8 9 10 11
不装任何商品 0 0 0 0 0 0 0 0 0 0 0 0
w1 = 1，v1 = 1 0 1 1 1 1 1 1 1 1 1 1 1
w2 = 2，v2 = 6 0 1 6 7 7 7 7 7 7 7 7 7
w3 = 5，v3 = 18 0 1 6 7 7 18 19 24 25 25 25 25
w4 = 6，v4 = 22 0 1 6 7 7 18 22 24 28 29 29 40
w5 = 7，v5 = 28 0 1 6 7 7 18 22 28 29 34 35 40


注意，并不是每试图装入一个新商品，背包的收益一定会提高。举个例子，承重为 7 斤的背包装入商品四时的最大收益是：f(7) = 22+f(1) = 23，装入商品三时最大的收益值为：f(7) = 18+f(2) = 24。因此，表 5 中承重 7 斤的背包装入商品 4 时对应的收益值仍为 24，并未发生改变。

代码实现:

  1. public class Demo {
  2.     static int N = 5;//商品的种类
  3.     static int W = 11;//背包的承重
  4.     //动态规划算法解决01背包问题
  5.     public static void knapsack01(int [][] result , int [] w,int []v) {
  6.         //逐个遍历每个商品
  7.         for(int i=1;i<=N;i++) {
  8.             //求出从 1 到 W 各个承重对应的最大收益
  9.             for ( int j=1;j<=W;j++) {
  10.                 //如果背包承重小于商品总重量，则该商品无法放入背包，收益不变
  11.                 if(j<w[i]) {
  12.                     result[i][j] = result[i-1][j];
  13.                 }else {
  14.                     //比较装入该商品和不装该商品，哪种情况获得的收益更大，记录最大收益值
  15.                     result[i][j] = result[i - 1][j] > (v[i] + result[i - 1][j - w[i]]) ? result[i - 1][j] : (v[i] + result[i - 1][j - w[i]]);
  16.                 }
  17.             }
  18.         }
  19.     }
  20.     //追溯选中的商品
  21.     public static void select(int [][] result , int [] w,int []v) {
  22.         int n = N;
  23.         int bagw = W;
  24.         //逐个商品进行判断
  25.         while(n>0) {
  26.             //如果在指定承重下，该商品对应的收益和上一个商品对应的收益相同，则表明未选中
  27.              if (result[n][bagw] == result[n - 1][bagw]) {
  28.                     n--;
  29.                 }
  30.                 else {
  31.                     //输出被选用商品的重量和价值
  32.                     System.out.print("("+w[n]+","+v[n]+") ");
  33.                     //删除被选用商品的承重，以便继续遍历
  34.                     bagw = bagw - w[n];
  35.                     n--;
  36.                 }
  37.         }
  38.     }
  39.     public static void main(String[] args) {
  40.         int [] w= {0,1 , 2 , 5 , 6 , 7}; //商品的重量
  41.         int [] v ={0,1 , 6 , 18 , 22 , 28};  //商品的价值
  42.         int [][] result = new int[N+1][W+1];
  43.         knapsack01(result, w, v);;
  44.         System.out.println("背包可容纳重量为 "+W+"，最大收益为 "+result[N][W]);
  45.         System.out.print("选择了");
  46.         select(result, w,v);
  47.     }
  48. }

程序结果：
image.png

5、迷宫问题

迷宫问题指的是：在给定区域内，找到一条甚至所有从某个位置到另一个位置的移动路线。举个简单的例子，如图 1 所示，在白色区域内找到一条（甚至所有）从起点到终点的路线。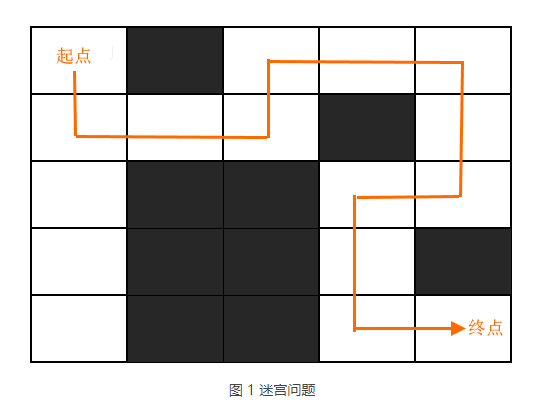
image.png

迷宫问题就可以采用回溯算法解决，即从起点开始，采用不断“回溯”的方式逐一试探所有的移动路线，最终找到可以到达终点的路线。
回溯算法解决迷宫问题
以图 1 所示的迷宫为例，回溯算法解决此问题的具体思路是：

  1. 从当前位置开始，分别判断是否可以向 4 个方向（上、下、左、右）移动：
  2. 选择一个方向并移动到下个位置。判断此位置是否为终点，如果是就表示找到了一条移动路线；如果不是，在当前位置继续判断是否可以向 4 个方向移动；
  3. 如果 4 个方向都无法移动，则回退至之前的位置，继续判断其它的方向；
  4. 重复 2、3 步，最终要么成功找到可行的路线，要么回退至起点位置，表明所有的路线都已经判断完毕。


程序中，我们可以用特殊的字符表示迷宫中的不同区域。例如，用 1 表示可以移动的白色区域，用 0 表示不能移动的黑色区域，图 1 的迷宫可以用如下的 0-1 矩阵来表示：

1 0 1 1 1
1 1 1 0 1
1 0 0 1 1
1 0 0 1 0
1 0 0 1 1

代码实现：

  1. public class Demo {
  2.     static boolean find = false;
  3.     static int ROW = 5;
  4.     static int COL = 5;
  5.     //(row,col) 表示起点，(outrow,outcol)表示终点
  6.     public static void maze_puzzle(char [][] maze, int row, int col, int outrow, int outcol) {
  7.         maze[row][col] = 'Y'; // 将各个走过的区域标记为 Y
  8.         //如果行走至终点，表明有从起点到终点的路线
  9.         if (row == outrow && col == outcol) {
  10.             find = true;
  11.             System.out.println("成功走出迷宫,路线图为：");
  12.             printmaze(maze);
  13.             return ;
  14.         }
  15.         //尝试向上移动
  16.         if (canMove(maze, row - 1, col)) {  
  17.             maze_puzzle(maze, row - 1, col, outrow, outcol);
  18.             //如果程序不结束，表明此路不通，恢复该区域的标记
  19.             maze[row - 1][col] = '1';
  20.         }
  21.         //尝试向左移动
  22.         if (canMove(maze, row, col - 1)) {
  23.             maze_puzzle(maze, row, col - 1, outrow, outcol);
  24.             //如果程序不结束，表明此路不通，恢复该区域的标记
  25.             maze[row][col - 1] = '1';
  26.         }
  27.         //尝试向下移动
  28.         if (canMove(maze, row + 1, col)) {
  29.             maze_puzzle(maze, row + 1, col, outrow, outcol);
  30.             //如果程序不结束，表明此路不通，恢复该区域的标记
  31.             maze[row + 1][col] = '1';
  32.         }
  33.         //尝试向右移动
  34.         if (canMove(maze, row, col + 1)) {
  35.             maze_puzzle(maze, row, col + 1, outrow, outcol);
  36.             //如果程序不结束，表明此路不通，恢复该区域的标记
  37.             maze[row][col + 1] = '1';
  38.         }
  39.     }
  40.     //判断(row,col)区域是否可以移动
  41.     public static boolean canMove(char [][] maze, int row, int col) {
  42.         //如果目标区域位于地图内，不是黑色区域，且尚未移动过，返回 true：反之，返回 false
  43.         return row >= 0 && row <= ROW - 1 && col >= 0 && col <= COL - 1 && maze[row][col] != '0' && maze[row][col] != 'Y';
  44.     }
  45.     //输出行走路线
  46.     public static void printmaze(char [][] maze) {
  47.         for(int i=0;i<ROW;i++) {
  48.             for(int j=0;j<COL;j++) {
  49.                 System.out.print(maze[i][j]+" ");
  50.             }
  51.             System.out.println();
  52.         }
  53.     }
  54.     public static void main(String[] args) {
  55.         char [][]maze = new char[][]{
  56.                 {'1','0','1','1','1'},
  57.                 {'1','1','1','0','1'},
  58.                 {'1','0','0','1','1'},
  59.                 {'1','0','0','1','0'},
  60.                 {'1','0','0','1','1'} };
  61.         maze_puzzle(maze, 0, 0, ROW - 1, COL - 1);
  62.         if (find == false) {
  63.             System.out.print("未找到可行线路");
  64.         }
  65.     }
  66. }

程序结果：
image.png
多个 Y 组成的路线就是从起点到终点的可行路线。

6、N皇后问题

N 皇后问题源自国际象棋，所有棋子中权力最大的称为皇后，它可以直着走、横着走、斜着走（沿 45 度角），可以攻击移动途中遇到的任何棋子。N 皇后问题的具体内容是：如何将 N 个皇后摆放在 N*N 的棋盘中，使它们无法相互攻击。

举个简单的例子，将 4 个皇后摆放在 4*4 的棋盘中，下图给出了一种摆放方式，各个皇后无论是直着走、横着走还是斜着走，都无法相互攻击。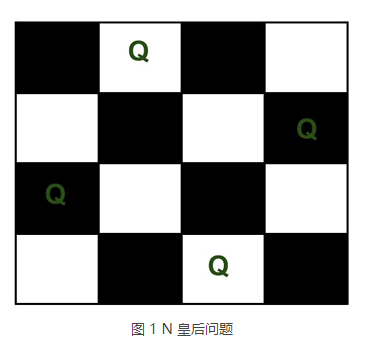
image.png

Q 表示放置皇后的位置。
N 皇后问题可以用回溯算法解决，接下来就为您讲解具体的解决思路。

回溯算法解决N皇后问题
要想使 N 个皇后不相互攻击，应将它们放置在不同的行、不同的列、还不能位于同一条 45°（或 135°）角的斜线上。
回溯算法解决N皇后问题的具体思路是：将 N 个皇后逐一放置在不同的行，以“回溯”的方式逐一测试出每行皇后所在行的具体位置，最终确定所有皇后的位置。

代码实现：

  1. import java.util.Scanner;
  3. public class Demo {
  4.     static int[] q = new int[20];
  5.     static int count = 0;
  7.     public static void n_queens(int k, int n) {
  8.         int j;
  9.         if (k > n)
  10.             print(n);
  11.         else {
  12.             for (j = 1; j <= n; j++) // 试探第k行的每一列，找到符合要求的列
  13.             {
  14.                 if (isSafe(k, j)) {
  15.                     q[k] = j;
  16.                     n_queens(k + 1, n); // 在确认第 k 行皇后位置的前提下，继续测试下一行皇后的位置
  17.                 }
  18.             }
  19.         }
  20.     }
  22.     public static boolean isSafe(int k, int j) {
  23.         int i;
  24.         for (i = 1; i < k; i++) {
  25.             // 如果有其它皇后位置同一列上，或者位于该位置的斜线位置上，则该位置无法使用
  26.             if (q[i] == j || Math.abs(i - k) == Math.abs(q[i] - j))
  27.                 return false;
  28.         }
  29.         return true;
  30.     }
  32.     // 输出 N 皇后问题的解决方案
  33.     public static void print(int n) {
  34.         int i, j;
  35.         count++;
  36.         System.out.println("第 " + count + " 个解：");
  38.         for (i = 1; i <= n; i++) // 行
  39.         {
  40.             for (j = 1; j <= n; j++) // 列
  41.             {
  42.                 if (q[i] != j)
  43.                     System.out.print("x");
  44.                 else
  45.                     System.out.print("Q");
  46.             }
  47.             System.out.println();
  48.         }
  49.         System.out.println();
  50.     }
  52.     public static void main(String[] args) {
  53.         System.out.println("请输入皇后个数：");
  54.         Scanner sc = new Scanner(System.in);
  55.         int n = sc.nextInt();
  56.         n_queens(1, n);
  57.         System.out.println("共有 " + count + " 种摆放方式");
  58.     }
  59. }

程序结果：
假设皇后的总个数为 4
image.png