对比红黑树

红黑树可以确保查询在O(log(n))内，但是它是一颗内存搜索树，在面对海量磁盘数据，海量外部数据时，很难将这些数据一次性加载到内存中进行搜索。

而B树在这方面进行了补充，由于搜索面临磁盘I/O读写的问题，而在内存搜索树中找到一个节点的次数跟树的高度保持正相关，降低树的高度则有效的减少磁盘I/O，提升了查询效率，为此B树转换成了一颗矮胖的树(相对而言)，精确查找则是在内存中进行。

性质

一个m阶的B树具有如下几个特征：

  • 根结点至少有两个子节点。
  • 每个中间节点都包含k-1个元素和k个孩子，其中 m/2 <= k <= m
  • 每一个叶子节点都包含k-1个元素，其中 m/2 <= k <= m
  • 所有的叶子结点都位于同一层。
  • 每个节点中的元素从小到大排列，节点当中k-1个元素正好是k个孩子包含的元素的值域分划。

其他

  • 元素(关键字)(数据): 保持在当前节点的数据
  • 孩子(子树): 当前节点的子树

一个五阶的B树，每个中间节点都包含二-四个元素和三-五个孩子，每一个叶子节点都包含二-四个元素。

演示地址

图

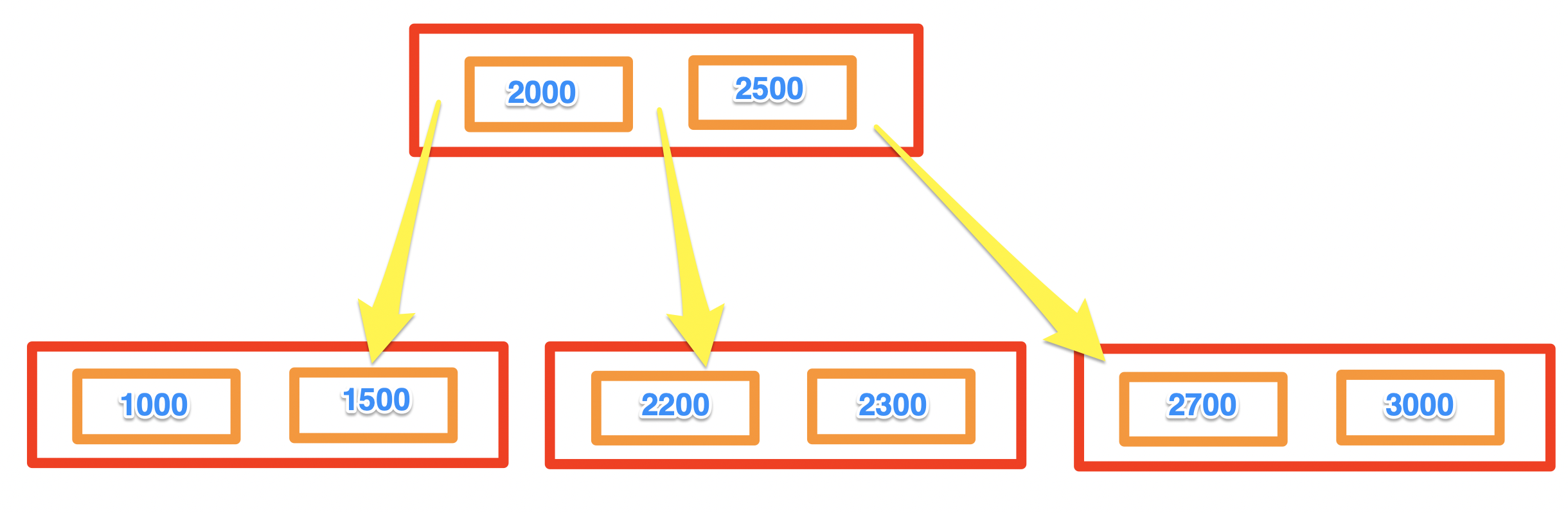image.png结构

  1. private final class Node {
  2.         //表明当前元素个数
  3.         public int numberOfNodes = 0；
  4.         //元素数组
  5.         public int key[];
  6.         //父亲节点
  7.         public Node parent;
  8.         //孩子指向
  9.         public Node children[];
  10.     }

全部代码

点我查看B树的基本实现全部代码

插入

B树的数据插入一定发生在树的叶子节点，如果叶子节点不满足性质，则递归的向上处理，分裂。

  • 找到待插入的叶子节点 (叶子节点元素的个数<=m-1)
  • 插入数据后，如果节点元素的个数<=m-1，直接返回，插入结束。否则进行第三步
  • 以节点中间key作为间限，分裂为2个子树，key的前半部分为左子树Left，key的后半部分为右子树Right，key元素成为父节点元素数据的一部分，孩子分别指向Left和Right。由于key元素上移，parent成为新插入节点，递归执行第二步。
    • 新分裂的左右节点的parent指向新产生的parent节点
    • 新分裂的左右节点的children指向node的children节点

      核心的节点分裂，如果分裂后导致元素上移的parent节点满了，继续分裂parent节点 语雀展现长代码块有Bug，查看代码的可以到Github上查看

删除

[m/2]=m/2向上取整; [5/2] = 3; [3/1]=2;

  • 富裕节点: 节点的元素个数 >= [m/2]-1 ;

B 🌲【B Tree】 - 图2

遍历

https://stackoverflow.com/questions/5890960/print-btree-by-level
遍历效果

  1.                        [1500]
  2.           [1300]                      [1700,1900]
  3.      [1200]     [1400]     [1600]     [1800]     [2000,2100]

参考链接