对比AVL树

AVL树在引入平衡因子后，已经可以确保时间复杂度在O(log(n))内了，但是每次插入和删除都可能会引起树的不平衡，从而引发AVL树旋转。

红黑树在AVL树的基础上相对又一点不一样的理念，不要求高度为1的平衡，转而追求红色和黑色之间的平衡。

两者都有其适用的场景，并不存在谁比谁强的情况。

基础性质

✅满足基本的二叉树性质

  • ✅ 节点是红色或黑色 【性质一】
  • ✅ 根是黑色 【性质二】
    • ✅ 所有叶子都是黑色(叶子是NIL节点)
  • ✅ 每个红色节点必须有两个黑色的子节点。(从每个叶子到根的所有路径上不能有两个连续的红色节点) 【性质三】
    • ✅ 这就可以理解所有叶子都是NIL节点(都是黑色)
    • ✅ 两个孩子节点都是黑色，自然不可能出现2个连续的红色节点
    • ✅ 红色节点的孩子节点必然是黑色,父亲节点必然是黑色
  • ✅ 从任一节点(父亲节点)到其每个叶子的所有简单路径)都包含相同数目的黑色节点。【性质四】
    • 为了保持性质四，新插入的节点都是红色节点


image.png

插入节点

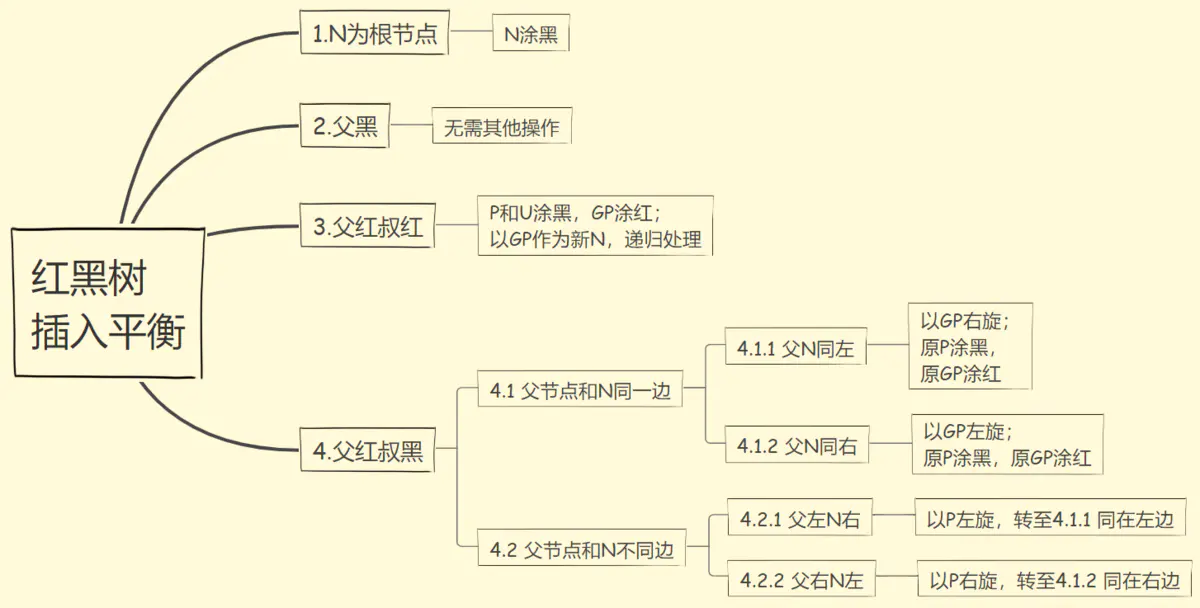
新插入的节点均为红色节点，因为红色不会影响路径上黑色节点的数量，保持性质四。如果父节点为黑色，就直接结束了；如果父节点为红色，则需要另外处理了。

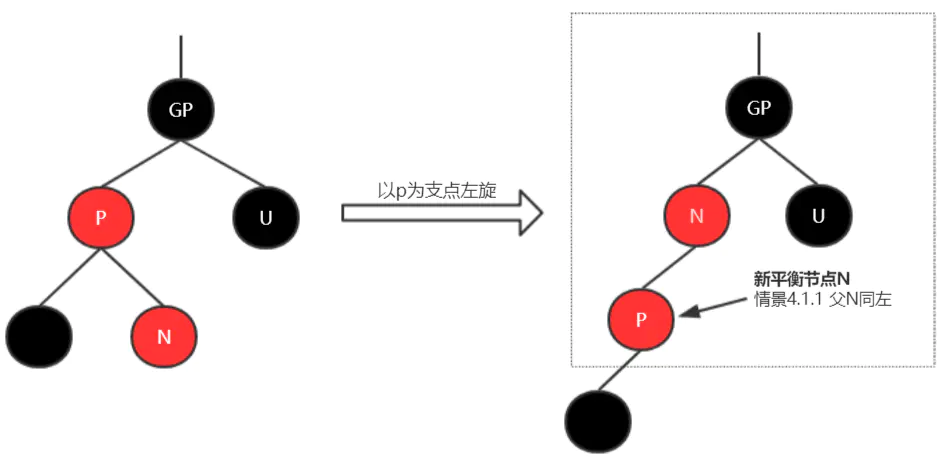
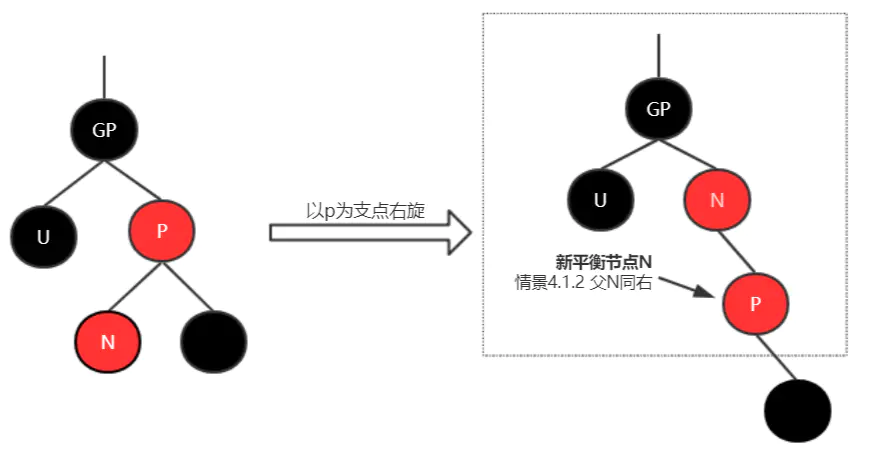
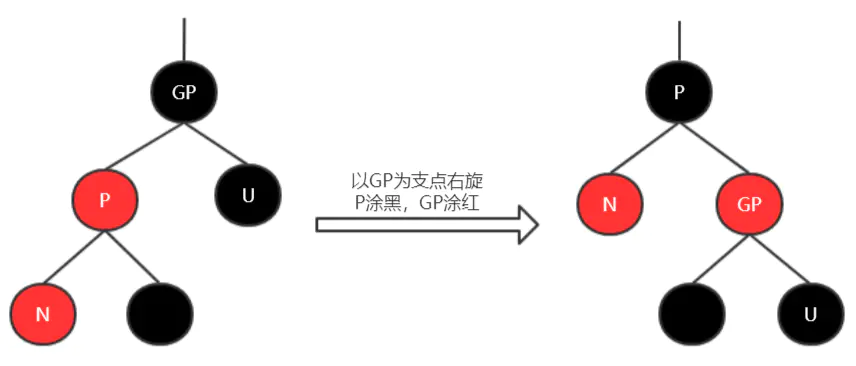  1.                      ![image.png](https://cdn.nlark.com/yuque/0/2021/png/191132/1629127235716-1884e1b0-c6bc-42dc-ab6b-7c940d2a5544.png#height=467&id=tjmil&margin=%5Bobject%20Object%5D&name=image.png&originHeight=608&originWidth=1200&originalType=binary&ratio=1&size=364860&status=done&style=shadow&width=921)
  4.        情形4.1.1![image.png](https://cdn.nlark.com/yuque/0/2021/png/191132/1629163109555-e0ca65de-b429-4e0f-957c-0a4281c5fbb0.png#height=183&id=weoMm&margin=%5Bobject%20Object%5D&name=image.png&originHeight=366&originWidth=856&originalType=binary&ratio=1&size=86132&status=done&style=none&width=428)            <br />情形4.1.2 ![image.png](https://cdn.nlark.com/yuque/0/2021/png/191132/1629163147618-1de66784-2665-4bba-bd73-098295cd88f3.png#height=173&id=UY7Ze&margin=%5Bobject%20Object%5D&name=image.png&originHeight=346&originWidth=815&originalType=binary&ratio=1&size=82533&status=done&style=none&width=407.5)

情形4.2.1 image.png
情形4.2.2 image.png

删除节点

节点删除存在三种情况

  • 待删除节点是叶子节点，即不存在子节点
    • 删除节点是红色节点，直接删除即可
    • 删除节点是黑色节点，需要进行平衡操作
      • 删除操作可能会导致红色节点只有一个黑色子节点了，可能路径上的黑色节点个数不一致了
  • 只有一个子节点，说明待删除节点一定是黑色节点，红色节点必须满足有2个黑色子节点，删除黑节点，将子节点的红色节点涂黑。
  • 存在两个子节点，找到左子树的最大值|右子树的最小值，替换即可，由于替换产生，这时情况转换为删除叶子或者删除一个子节点的情况

基于下图基本上可以实现红黑树的删除操作。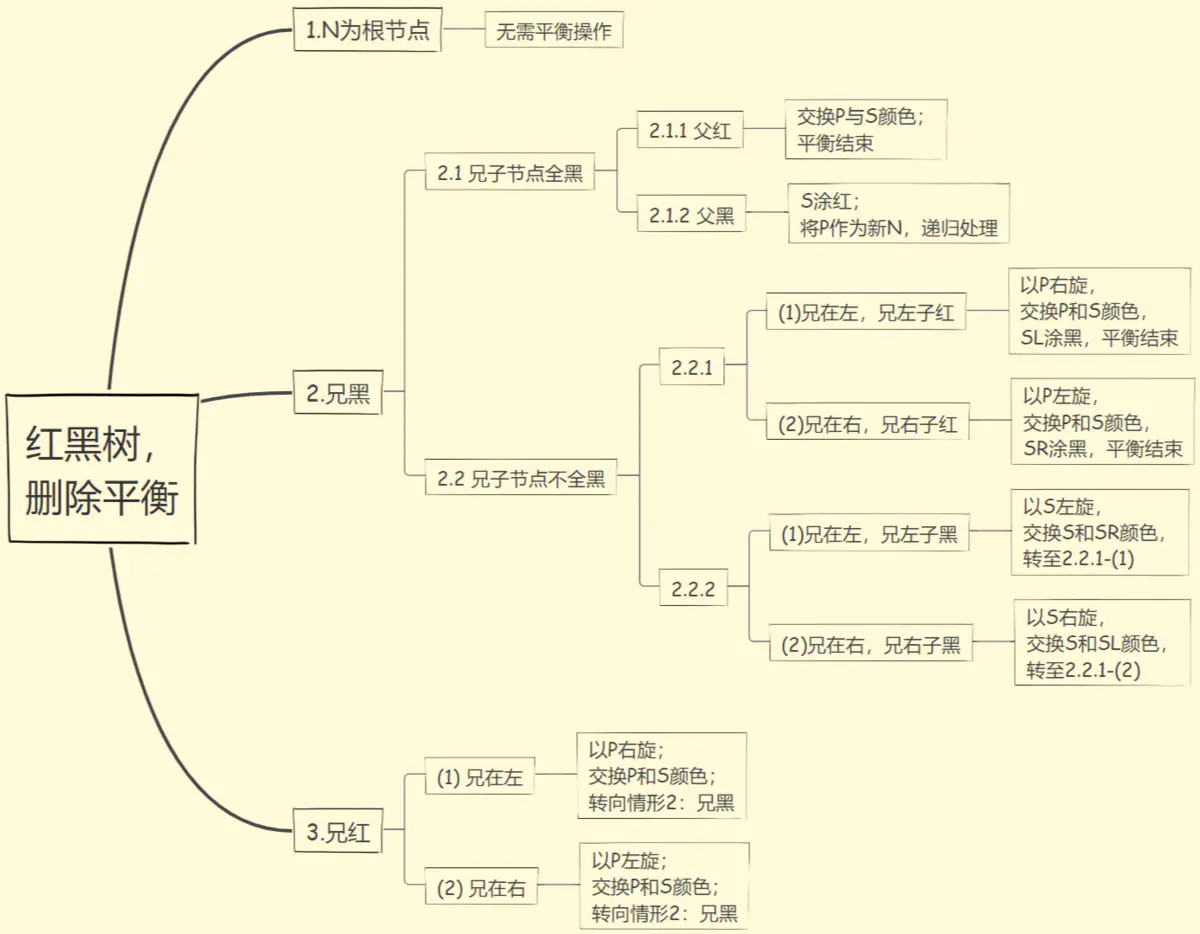
image.png

红黑树平衡一定要满足的性质

  • 红色节点必须有两个黑色子节点，红色为叶子也是有NIL节点,不过可以忽略。
  • 从任一节点到每个叶子节点的黑色节点个数保持一致

代码实现

插入节点顺序 20 ，10 ， 30 ， 1， 2， 3， 4， 5， 6， 7 实现效果如下

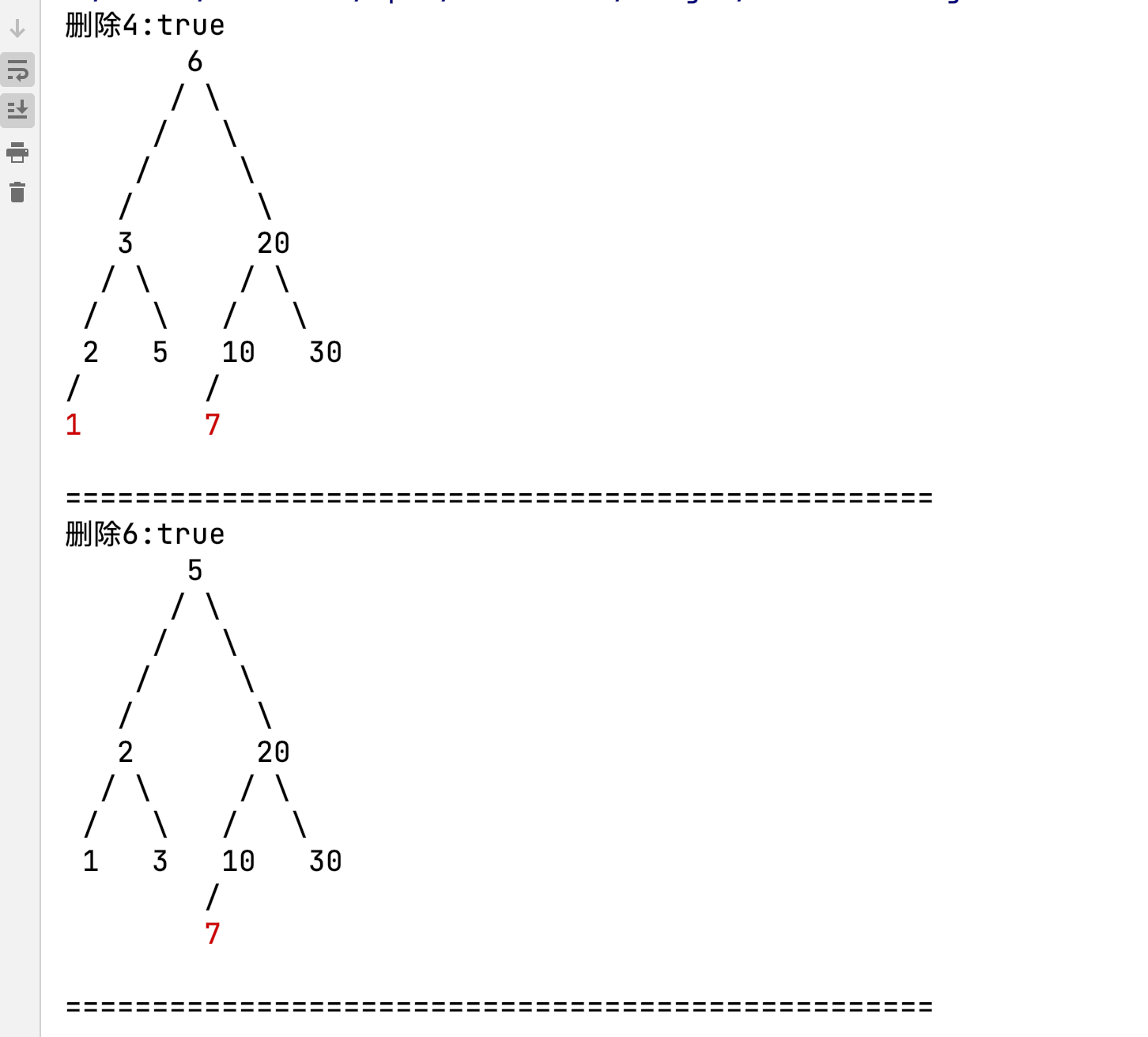
image.png
由于代码较长 (没有做啥优化，大概在600行左右)，这里放部分代码，完整代码 这里RedBlackTree.java

  • 插入节点后进行着色

  • 删除黑色叶子节点的过程

    1.   /**
    2.    * 插入节点后进行着色
    3.    */
    4.   private void coloringNode(Node node) {
    5.       if (node == null) {
    6.           return;
    7.       }
    8.       //1、节点N的parent节点(root)
    9.       Node parent = node.parent;
    10.       if (parent == null) {
    11.           node.black = true;
    12.           return;
    13.       }
    14.       //2、父黑 无需其他操作
    15.       if (parent.black) {
    16.           return;
    17.       }
    18.       //3、叔叔节点 父亲红叔叔红的情况
    19.       Node uncle = getUncle(parent);
    20.       //
    21.       if (!node.black && !uncleIsBlack(uncle)) {
    22.           parent.black = true;
    23.           uncle.black = true;
    24.           if (parent.parent != null) {
    25.               parent.parent.black = false;
    26.               coloringNode(parent.parent);
    27.           }
    28.           return;
    29.       }
    30.       Node p = parent;
    31.       do {
    32.           if (parent.black) {
    33.               //4、父亲红 叔叔黑
    34.               //4.1、父亲和N在同一边
    35.               //4.1.1、父亲和N都在左边
    36.               final Node gp = parent;
    37.               if (gp.leftChild == p && p.leftChild == node) {
    38.                   rr(gp, parent == root);
    39.               } else if (gp.rightChild == p && p.rightChild == node) {
    40.                   //4.1.2、父亲和N都在右边
    41.                   ll(gp, parent == root);
    42.               } else if (gp.leftChild == p && p.rightChild == node) {
    43.                   //4.2.1、父亲左，N在右
    44.                   lr(gp.leftChild, parent == root);
    45.               } else if (gp.rightChild == p && p.leftChild == node) {
    46.                   //4.2.2、父亲右，N在左
    47.                   rl(gp.rightChild, parent == root);
    48.               } else {
    49.                   throw new IllegalStateException("不应该跑到这里");
    50.               }
    51.               break;
    52.           }
    53.           parent = parent.parent;
    54.       } while (parent != null);
    55.   }
    56. //==================================================================================================
    57. //删除节点
    58.   /**
    59.    * 待删除节点为黑色叶子节点
    60.    *
    61.    * @param node 节点N,N为3
    62.    */
    63.   private void deleteBlackLeaf(Node node) {
    64.       //查询当前节点为parent的左节点还是右节点
    65.       //parent节点为2
    66.       final Node parent = node.parent;
    67.       //node3是parent2的右子
    68.       boolean isRight = node != parent.leftChild;
    69.       //1、获取兄弟节点
    70.       //获取兄弟节点，如果当前节点是左子，那么兄弟节点就是右子，反之亦然
    71.       //sibling为1
    72.       Node sibling = isRight ? parent.leftChild : parent.rightChild;
    73.       //2、兄弟节点为黑色
    74.       if (sibling.black) {
    75.           //2.1、兄子节点全黑
    76.           if (childAllBlack(sibling)) {
    77.               //2.1.1、父亲为红色
    78.               if (!parent.black) {
    79.                   changeNodeDir(node);
    80.                   //交换P和S的颜色,这里因为上边的判断所以可以直接判定
    81.                   parent.black = true;
    82.                   sibling.black = false;
    83.               } else {
    84.                   //2.1.2、父亲为黑色
    85.                   //兄弟节点S涂红
    86.                   changeNodeDir(node);
    87.                   sibling.black = false;
    88.                   //将P作为新的N，进行递归处理
    89.                   deleteBlackLeaf(parent);
    90.               }
    91.           } else {
    92.               //2.2、兄子节点不全黑
    93.               //isRight(true)当前节点在右，兄在左
    94.               if (isRight) {
    95.                   //2.2.1 兄在左，兄左子红
    96.                   final Node sl = sibling.leftChild;
    97.                   boolean red = sl != null && !sl.black;
    98.                   if (red) {
    99.                       //以当前节点的parent节点右旋，右旋完成后交互P和S的颜色，SL涂黑 平衡结束
    100.                       rrNotColor(parent, parent == root);
    101.                       final boolean parentColor = parent.black;
    102.                       parent.black = sibling.black;
    103.                       sibling.black = parentColor;
    104.                       sibling.leftChild.black = true;
    105.                       //为了兼容处理删除含2个子节点的数据，这里是调整删除nil节点
    106.                       if (node.nil) {
    107.                           changeNodeDir(node);
    108.                       }
    109.                   } else {
    110.                       //2.2.2 兄弟节点在左,兄弟节点左子树黑
    111.                       final Node SR = sibling.rightChild;
    112.                       final Node SL = sibling.leftChild;
    113.                       //以兄弟节点S左旋
    114.                       llNotColor(sibling, false);
    115.                       //交换S和SR的颜色
    116.                       final boolean srColor = SR.black;
    117.                       SR.black = sibling.black;
    118.                       sibling.black = srColor;
    120.                       deleteBlackLeaf(node);
    121.                   }
    122.               } else {
    123.                   //2.2.2、兄在右(既成事实)
    124.                   final Node sr = sibling.rightChild;
    125.                   boolean red = sr != null && !sr.black;
    126.                   if (red) {
    127.                       //以P左旋，交换P和S的颜色，SR涂黑，平衡结束
    128.                       llNotColor(parent, parent == root);
    129.                       final boolean parentColor = parent.black;
    130.                       parent.black = sibling.black;
    131.                       sibling.black = parentColor;
    132.                       sibling.rightChild.black = true;
    133.                       if (node.nil) {
    134.                           changeNodeDir(node);
    135.                       }
    136.                   } else {
    137.                       final Node SL = sibling.leftChild;
    138.                       //以S右旋
    139.                       rrNotColor(sibling, false);
    140.                       //交换S和SL颜色
    141.                       final boolean slColor = sibling.black;
    142.                       sibling.black = SL.black;
    143.                       SL.black = slColor;
    145.                       deleteBlackLeaf(node);
    146.                   }
    147.               }
    148.           }
    149.       } else {
    150.           //3、兄弟节点为红色
    151.           //3.1、兄弟节点在左
    152.           //isRight(true)当前节点在右，兄在左
    153.           if (isRight) {
    154.               llNotColor(parent, parent == root);
    155.           } else {
    156.               //3.2、兄弟节点在右
    157.               rrNotColor(parent, parent == root);
    158.           }
    159.           final boolean parentColor = parent.black;
    160.           parent.black = sibling.black;
    161.           sibling.black = parentColor;
    162.           deleteBlackLeaf(parent);
    163.       }
    164.   }

    参考链接

    图片来源于下链接，讲解和配图都很不错的。