目录

1 简介

概念： 是分类变量的分类算法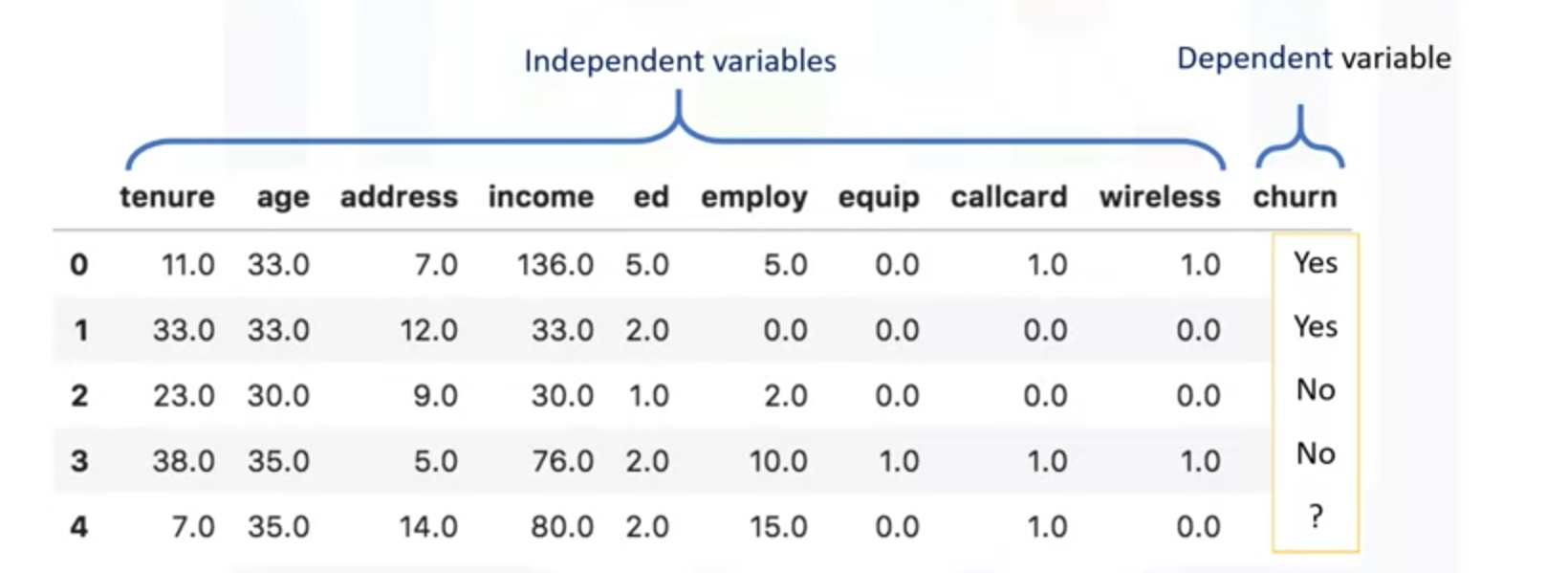

2 逻辑回归的应用

（1）预测某人是否有心脏病
（2）预测病人的致死率
（3）预测用户的购买意向
（4）预测工程或产品的失败率
（5）预测房主拖欠抵押贷款的可能性

3 逻辑回归的适用范围

（1）两面性的问题
（2）需要计算可能性
（3）需要一个线性决策边界
（4）需要理解某个功能的影响

4 逻辑回归与线性回归的区别联系

• 线性回归和逻辑回归都是广义线性回归模型的特例
• 线性回归只能用于回归问题，逻辑回归用于分类问题（可由二分类推广至多分类）
• 线性回归无联系函数或不起作用，逻辑回归的联系函数是对数几率函数，属于Sigmoid函数

• 线性回归使用最小二乘法作为参数估计方法，逻辑回归使用极大似然法作为参数估计方法

  5 逻辑回归训练

  （1）步骤

• 第一步：随机初始化参数

• 第二步：用训练集计算损失函数，然后计算误差

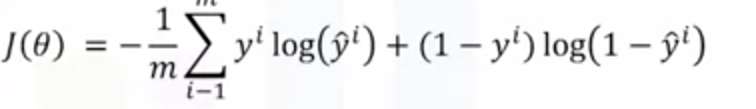
• 第三步：计算损失函数的梯度

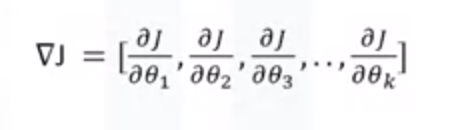
• 第四步：用梯度更新参数

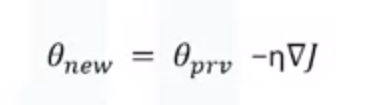
• 第五步：回到第二步，直到损失函数足够小
• 第六步：运用模型进行预测结果

（2）一般损失函数

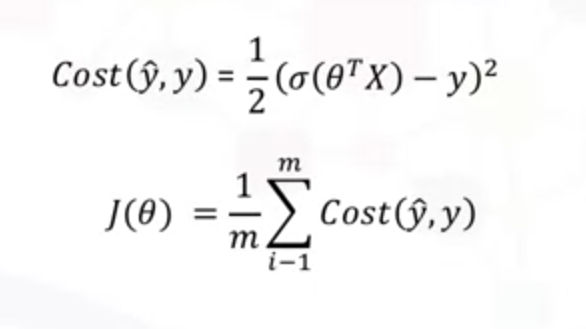
（3）画出损失函数模型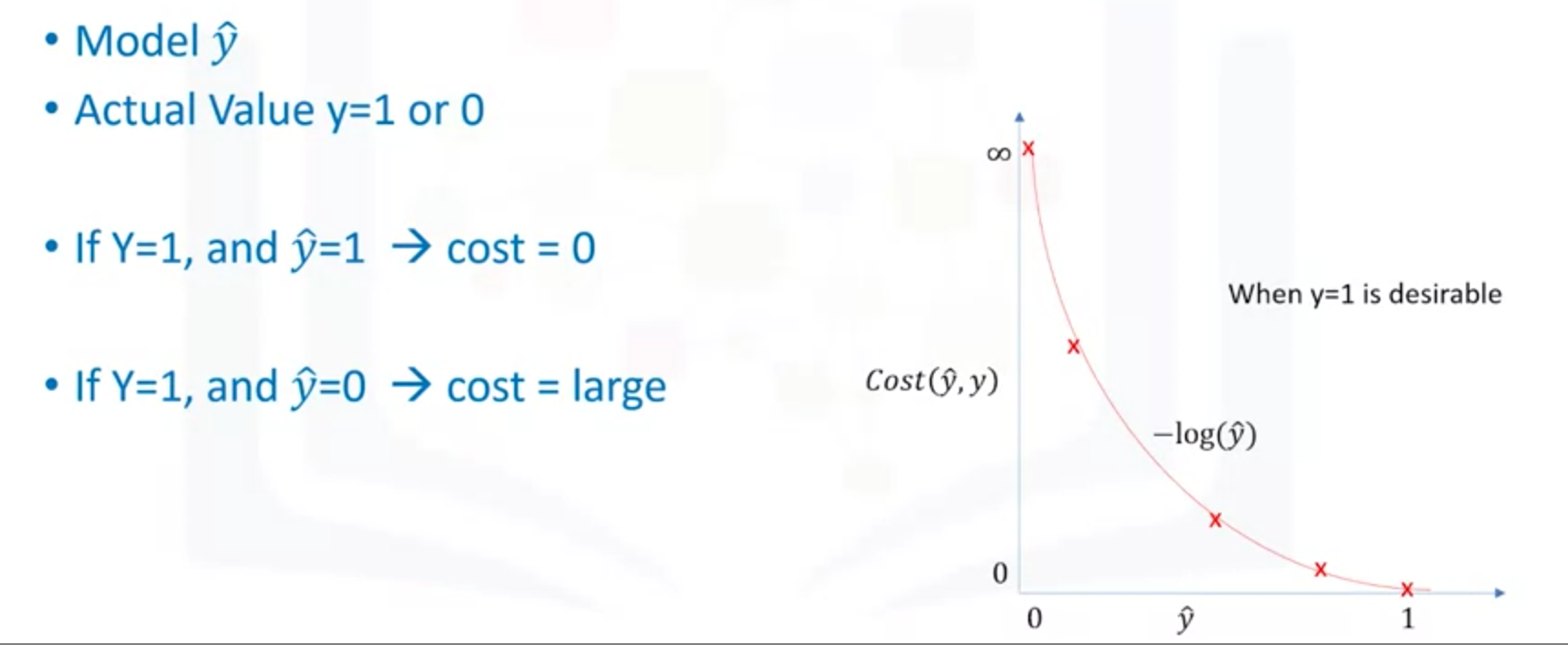

（4）逻辑回归损失函数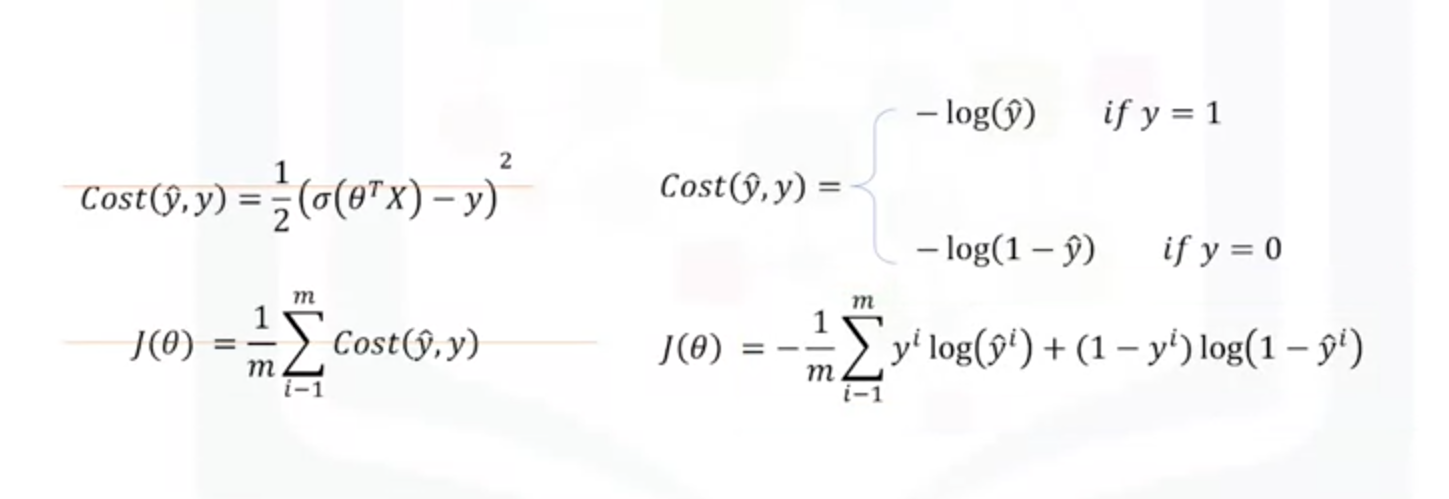

（5）最小化模型损失函数

• 如何找到模型最合适的参数？最小化损失函数
• 如何最小化损失函数？优化方法中的一种。使用梯度下降
• 梯度下降是什么？是一种为了最小化损失函数，通过求损失函数的微分去改变参数值的技术。

（6）使用梯度下降最小化损失函数举例

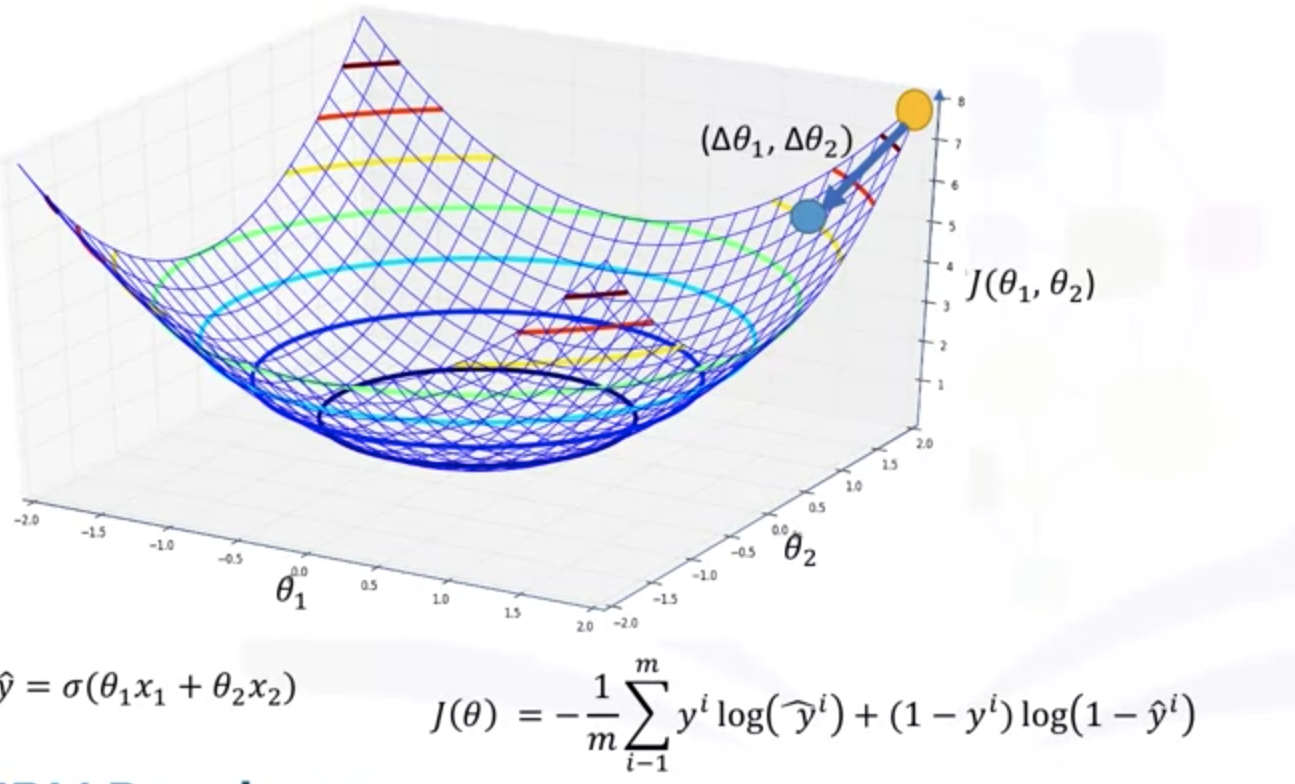
求所有下一个位置的偏导数，根据这些数据去找到损失函数的最小值。