1 二值神经网络简介
1.1 优势
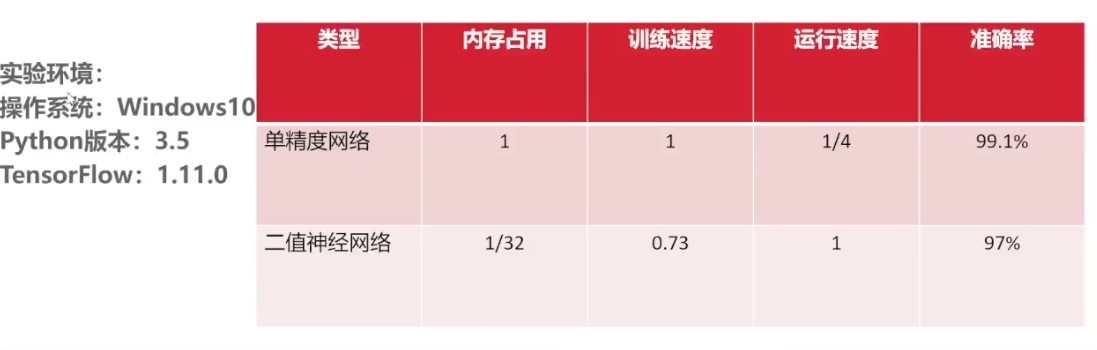
(1)内存占用
权重矩阵二值化(仅为-1和1),一个权重值只占一个比特,详单与单精度浮点型权重矩阵,网络模型的内存消耗理论上能减少32倍,因此二值神经网络在模型压缩上具有很大的优势
(2)计算速度
当权重值和激活函数值同时进行二值化之后,原来32位浮点型数的乘加运算,可以通过一次异或运算解决,在模型加速上具有很大的潜力。
2 论文
《Binarized Neural Networks: Training Deep Neural Networks with Weights and Activations Constrained to +1 or -1》
2 二值神经网络的实现
2.1 如何二值化
两种方式,决定式的二值化和随机式的二值化
(1)决定式的二值化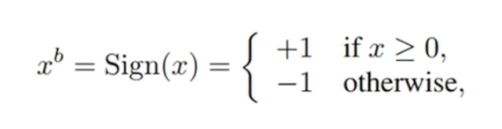
一个简单的二值化例子:当权重是大于0的,二值化为1,小于0的二值化为-1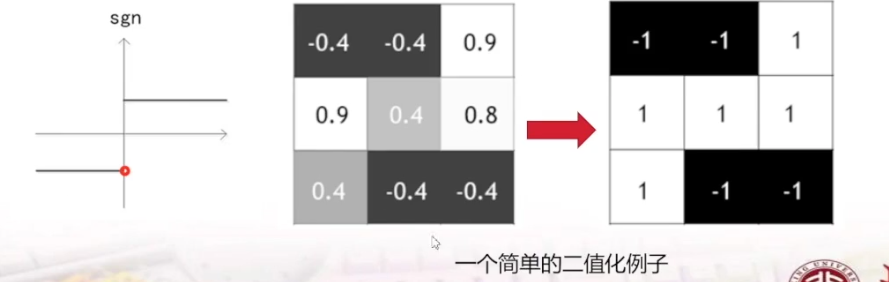
2.2 如何求梯度
问题:直接对决定式的二值化函数求导,求导厚点值都是0
解决办法:引入l= Htanh(x)函数来支持反向传播,假设损失函数为C,且已知C对q求导,那么C对r的求导如下:
表示【-1 1】区间,l=1,在其他区间l =0,则梯度根据以下公式去求 。
3 网络结构
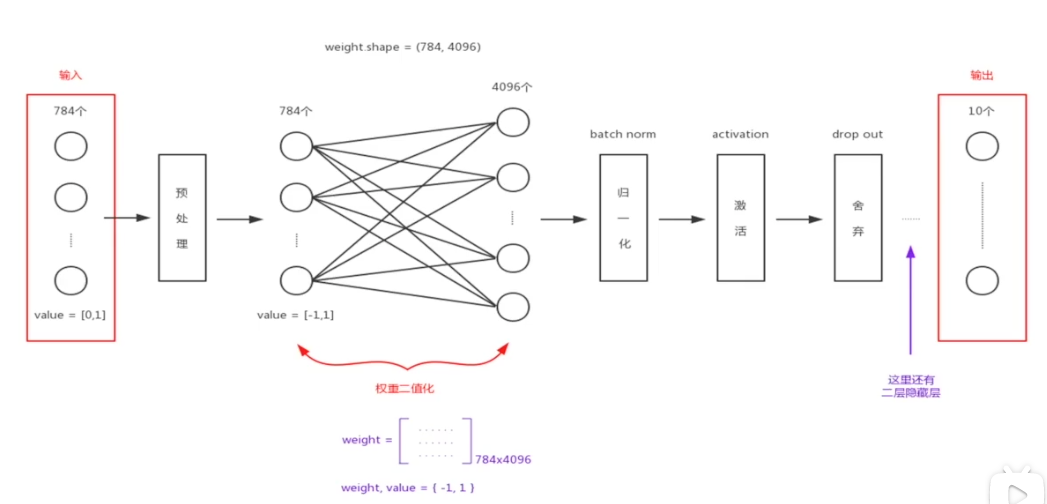
输入像素是784。因为MNIST数据集的像素值是位于【0 1】之间,就需要做预处理把像素值抓换到【-1 1】区间去适应神经网络
4 实现
mnist_train.py文件
加载mnist数据集像素值范围
# convert class vectors to binary class vectorsfor i in range(mnist.train.images.shape[0]):mnist.train.images[i] = mnist.train.images[i] * 2 - 1for i in range(mnist.test.images.shape[0]):mnist.test.images[i] = mnist.test.images[i] * 2 - 1for i in range(mnist.train.labels.shape[0]):mnist.train.labels[i] = mnist.train.labels[i] * 2 - 1 # -1 or 1 for hinge lossfor i in range(mnist.test.labels.shape[0]):mnist.test.labels[i] = mnist.test.labels[i] * 2 - 1
神经网络结构
# 添加三层隐藏层,并做dropout# 输入层dropoutlayer0 = no_scale_dropout(x, drop_rate=0.2, training=training)# 添加一层隐藏层layer1 = fully_connect_bn(layer0, 4096, act=binary.binary_tanh_unit, use_bias=True, training=training)layer1_dp = no_scale_dropout(layer1, drop_rate=0.5, training=training)# 添加一层隐藏层layer2 = fully_connect_bn(layer1_dp, 4096, act=binary.binary_tanh_unit, use_bias=True, training=training)layer2_dp = no_scale_dropout(layer2, drop_rate=0.5, training=training)# 添加一层隐藏层layer3 = fully_connect_bn(layer2_dp, 4096, act=binary.binary_tanh_unit, use_bias=True, training=training)layer3_dp = no_scale_dropout(layer3, drop_rate=0.5, training=training)# 添加输出层layer4 = fully_connect_bn(layer3_dp, 10, act=None, use_bias=True, training=training)#out_act_training = tf.nn.softmax_cross_entropy_with_logits(logits=layer4, labels=target)#out_act_testing = tf.nn.softmax(logits=layer4)#out_act = tf.cond(training, lambda: out_act_training, lambda: out_act_testing)# 损失函数(y_label*layer4即对应元素相乘再相加)loss = tf.reduce_mean(tf.square(tf.maximum(0.,1.-target*layer4)))
Adam优化算法。使用两个优化器:因为将变量分为两部分更新,一部分(权重)使用binary.AdamOptimizer,一部分(偏置,归一化用到的参数等)用tf.train.AdamOptimizer
other_var = [var for var in tf.trainable_variables() if not var.name.endswith('kernel:0')]opt = binary.AdamOptimizer(binary.get_all_LR_scale(), lr1)opt2 = tf.train.AdamOptimizer(lr2)update_ops = tf.get_collection(tf.GraphKeys.UPDATE_OPS)with tf.control_dependencies(update_ops): # when training, the moving_mean and moving_variance in the BN need to be updated.#将变量分为两部分更新,一部分(权重)使用binary.AdamOptimizer,一部分(偏置,归一化用到的参数等)用tf.train.AdamOptimizertrain_kernel_op = opt.apply_gradients(binary.compute_grads(loss, opt), global_step=global_step1)train_other_op = opt2.minimize(loss, var_list=other_var, global_step=global_step2)
5 结果分析
根据右下角的图说明二值神经网络需要更多的迭代次数才可以达到全精度网络的准确率。但是根据左下角的图可以看到,在速度上二值神经网络有绝对的优势。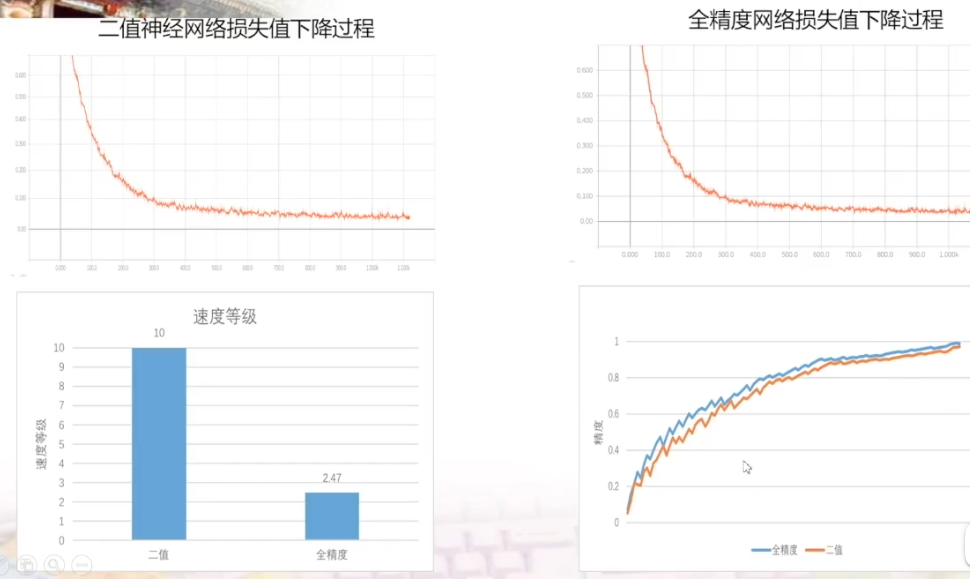
项目总结:二值神经网络内存占用小很多,训练速度快很多,运行速度快很多,准确率偏低