目录

1.2 举例理解

截屏2020-12-19 下午7.45.28.png
代码实现

  1. #coding:utf-8
  2. #设损失函数 loss=(w+1)^2, 令w初值是常数5。反向传播就是求最优w，即求最小loss对应的w值
  3. import tensorflow as tf
  4. #定义待优化参数w初值赋5
  5. w = tf.Variable(tf.constant(5, dtype=tf.float32))
  6. #定义损失函数loss
  7. loss = tf.square(w+1)#tf.square()是对a里的每一个元素求平方
  8. #定义反向传播方法
  9. train_step = tf.train.GradientDescentOptimizer(0.2).minimize(loss)
  10. #生成会话，训练40轮
  11. with tf.Session() as sess:
  12.     init_op=tf.global_variables_initializer()#初始化
  13.     sess.run(init_op)#初始化
  14.     for i in range(40):#训练40轮
  15.         sess.run(train_step)#训练
  16.         w_val = sess.run(w)#权重
  17.         loss_val = sess.run(loss)#损失函数
  18.         print("After %s steps: w is %f,   loss is %f." % (i, w_val,loss_val))#打印

1.3 学习率的选择

学习率大了震荡不收敛，学习率小了，收敛速度慢。
因此提出指数衰减学习率

  1. learning_rate =LEARNING_RATE_BASE*LEARNING_RATE_OECAY
  2. #其中LEARNING_RATE_OECAY = Batch_size/Learning_rate_step(运行了几轮/多少轮更新一次学习率)其中Learning_rate_size 也等于总样本数/Batch_size

截屏2020-12-19 下午7.50.15.png

  1. #coding:utf-8
  2. #设损失函数 loss=(w+1)^2, 令w初值是常数10。反向传播就是求最优w，即求最小loss对应的w值
  3. #使用指数衰减的学习率，在迭代初期得到较高的下降速度，可以在较小的训练轮数下取得更有收敛度。
  4. import tensorflow as tf
  6. LEARNING_RATE_BASE = 0.1 #最初学习率
  7. LEARNING_RATE_DECAY = 0.99 #学习率衰减率
  8. LEARNING_RATE_STEP = 1  #喂入多少轮BATCH_SIZE后，更新一次学习率，一般设为：总样本数/BATCH_SIZE
  10. #运行了几轮BATCH_SIZE的计数器，初值给0, 设为不被训练
  11. global_step = tf.Variable(0, trainable=False)
  12. #定义指数下降学习率
  13. learning_rate = tf.train.exponential_decay(LEARNING_RATE_BASE, global_step, LEARNING_RATE_STEP, LEARNING_RATE_DECAY, staircase=True)
  14. #定义待优化参数，初值给10
  15. w = tf.Variable(tf.constant(5, dtype=tf.float32))
  16. #定义损失函数loss
  17. loss = tf.square(w+1)#tf.square()是对a里的每一个元素求平方
  18. #定义反向传播方法    使用minimize()操作，该操作不仅可以优化更新训练的模型参数，也可以为全局步骤(global_step)计数   
  19. train_step = tf.train.GradientDescentOptimizer(learning_rate).minimize(loss, global_step=global_step)
  20. #生成会话，训练40轮
  21. with tf.Session() as sess:
  22.     init_op=tf.global_variables_initializer()#初始化
  23.     sess.run(init_op)
  24.     for i in range(40):#40次
  25.         sess.run(train_step)#训练
  26.         learning_rate_val = sess.run(learning_rate)#学习率
  27.         global_step_val = sess.run(global_step)#计算获取计数器的值
  28.         w_val = sess.run(w)#计算权重
  29.         loss_val = sess.run(loss)#计算损失函数
  30.         #打印相应数据
  31.         print ("After %s steps: global_step is %f, w is %f, learning rate is %f, loss is %f" % (i, global_step_val, w_val, learning_rate_val, loss_val))

2 滑动平均

2.1 概念

滑动平均（影子值）：记录了每个参数一段时间内国王值的平均，增加了模型泛化性。
针对权重和偏（像是给参数加了影子，参数变化，影子缓慢追随）
截屏2020-12-19 下午8.00.02.png
举例如下
截屏2020-12-19 下午8.02.10.png

2.2 滑动平均的实现

核心代码

  1. ema = tf.train.ExponentialMovingAverage(衰减率MOVING_AVERAGE_DECAY, 当前轮数global_step)#滑动平均
  3. ema_op = ema.apply(tf.trainable_variables())#每运行此句，所有待优化的参数求滑动平均
  4. # 通常我们把滑动平均与训练过程绑定在一起，使它们合成一个训练节点。如下所示
  5. with tf.control_dependencies([train_step,ema_op]):
  6.     train_op = tf.no_op(name='train')
  7. # ema.average(参数名)查看某参数的滑动平均值

完整的代码

  1. #coding:utf-8
  2. #tensorflow学习笔记(北京大学) tf4_6.py 完全解析  滑动平均
  3. #QQ群：476842922（欢迎加群讨论学习）
  4. #如有错误还望留言指正，谢谢🌝
  5. import tensorflow as tf
  7. #1. 定义变量及滑动平均类
  8. #定义一个32位浮点变量，初始值为0.0  这个代码就是不断更新w1参数，优化w1参数，滑动平均做了个w1的影子
  9. w1 = tf.Variable(0, dtype=tf.float32)
  10. #定义num_updates（NN的迭代轮数）,初始值为0，不可被优化（训练），这个参数不训练
  11. global_step = tf.Variable(0, trainable=False)
  12. #实例化滑动平均类，给衰减率为0.99，当前轮数global_step
  13. MOVING_AVERAGE_DECAY = 0.99
  14. ema = tf.train.ExponentialMovingAverage(MOVING_AVERAGE_DECAY, global_step)#滑动平均
  15. #ema.apply后的括号里是更新列表，每次运行sess.run（ema_op）时，对更新列表中的元素求滑动平均值。
  16. #在实际应用中会使用tf.trainable_variables()自动将所有待训练的参数汇总为列表
  17. #ema_op = ema.apply([w1])
  18. #apply(func [, args [, kwargs ]]) 函数用于当函数参数已经存在于一个元组或字典中时，间接地调用函数。
  19. ema_op = ema.apply(tf.trainable_variables())
  21. #2. 查看不同迭代中变量取值的变化。
  22. with tf.Session() as sess:
  23.     # 初始化
  24.     init_op = tf.global_variables_initializer()#初始化
  25.     sess.run(init_op)#计算初始化
  26.     #用ema.average(w1)获取w1滑动平均值 （要运行多个节点，作为列表中的元素列出，写在sess.run中）
  27.     #打印出当前参数w1和w1滑动平均值
  28.     print "current global_step:", sess.run(global_step)#打印global_step
  29.     print "current w1", sess.run([w1, ema.average(w1)]) #计算滑动平均
  31.     # 参数w1的值赋为1
  32.     #tf.assign(A, new_number): 这个函数的功能主要是把A的值变为new_number
  33.     sess.run(tf.assign(w1, 1))
  34.     sess.run(ema_op)
  35.     print "current global_step:", sess.run(global_step)
  36.     print "current w1", sess.run([w1, ema.average(w1)]) 
  38.     # 更新global_step和w1的值,模拟出轮数为100时，参数w1变为10, 以下代码global_step保持为100，每次执行滑动平均操作，影子值会更新 
  39.     sess.run(tf.assign(global_step, 100))  #设置global_step为100
  40.     sess.run(tf.assign(w1, 10))#设置W1为10
  41.     sess.run(ema_op)#运行ema_op
  42.     print "current global_step:", sess.run(global_step)#打印
  43.     print "current w1:", sess.run([w1, ema.average(w1)])  #打印     
  45.     # 每次sess.run会更新一次w1的滑动平均值
  46.     sess.run(ema_op)
  47.     print "current global_step:" , sess.run(global_step)
  48.     print "current w1:", sess.run([w1, ema.average(w1)])
  50.     sess.run(ema_op)
  51.     print "current global_step:" , sess.run(global_step)
  52.     print "current w1:", sess.run([w1, ema.average(w1)])
  54.     sess.run(ema_op)
  55.     print "current global_step:" , sess.run(global_step)
  56.     print "current w1:", sess.run([w1, ema.average(w1)])
  58.     sess.run(ema_op)
  59.     print "current global_step:" , sess.run(global_step)
  60.     print "current w1:", sess.run([w1, ema.average(w1)])
  62.     sess.run(ema_op)
  63.     print "current global_step:" , sess.run(global_step)
  64.     print "current w1:", sess.run([w1, ema.average(w1)])
  66.     sess.run(ema_op)
  67.     print "current global_step:" , sess.run(global_step)
  68.     print "current w1:", sess.run([w1, ema.average(w1)])
  70. #更改MOVING_AVERAGE_DECAY 为 0.1  看影子追随速度
  72. """
  74. current global_step: 0
  75. current w1 [0.0, 0.0]
  76. current global_step: 0
  77. current w1 [1.0, 0.9]
  78. current global_step: 100
  79. current w1: [10.0, 1.6445453]
  80. current global_step: 100
  81. current w1: [10.0, 2.3281732]
  82. current global_step: 100
  83. current w1: [10.0, 2.955868]
  84. current global_step: 100
  85. current w1: [10.0, 3.532206]
  86. current global_step: 100
  87. current w1: [10.0, 4.061389]
  88. current global_step: 100
  89. current w1: [10.0, 4.547275]
  90. current global_step: 100
  91. current w1: [10.0, 4.9934072]
  93. """

3 正则化

3.1 概念

利用正则化缓解过拟合：正则化在损失函数中引入模型复杂度指标，利用给W加权值，弱化了训练数据的噪声（一般不正则化b偏置）
截屏2020-12-19 下午8.14.15.png

3.2 实现

  1. #正则化法有两种，l1和l2，在使用时，二选一
  2. tf.contrib.layers.l1_regularizer(regularizer)(w)
  3. l2_regularizer(regularizer)(w)
  5. # 使用方式如下
  6. tf.add_to_collection('losses', tf.contrib.layers.l1_regularizer(regularizer)(w))
  7. loss = cem +tf.add_n(tf.get_collection('losses'))

3.3 举例

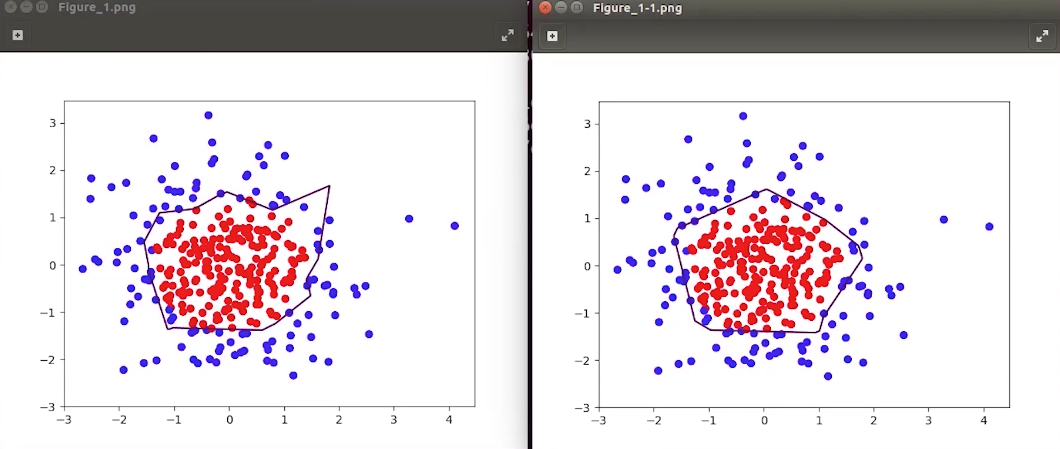
数据X[x0,x1]为正态分布随机点，标注Y当【北京大学】6 TensorFlow1.x的学习率、滑动平均和正则化实例及实现 - 图7时y= 1(标记为红色)，其余y_=0(标记未蓝色)
其中涉及一个可视化模块的使用如下

  1. import matplotlib.pyplot as plt
  2. #用各行Y_c对应的值表示颜色（c是color的缩写） 
  3. plt.scatter(X坐标, y坐标, c=np.squeeze(Y_c)) 
  4. plt.show()
  6. # 形成网格坐标点
  7. xx, yy = np.mgrid[起：止：步长，起：止：步长]
  8. # 降低维度，说直白点就是把数据拉直
  9. # x，y坐标进行配对
  10. grid = np.c_[xx.rave(),yy.ravel()]# np.c_表示组成矩阵，xx.rave(),yy.ravel()表示拉直
  11. # 把手机的网格坐标点，进行训练
  12. probs = sess.run(y,feed_dict={x:grid})
  13. probs = probs.reshape(xx.shape)
  14. # 给点上色
  15. plt.contour(x轴坐标值，y轴坐标值，该点的高度，levels =[等高线的高度])
  16. plt.show()

完成实现如下

  1. #coding:utf-8
  2. #0导入模块 ，生成模拟数据集
  3. import tensorflow as tf
  4. import numpy as np
  5. import matplotlib.pyplot as plt
  6. BATCH_SIZE = 30 
  7. seed = 2 
  8. #基于seed产生随机数
  9. rdm = np.random.RandomState(seed)
  10. #随机数返回300行2列的矩阵，表示300组坐标点（x0,x1）作为输入数据集
  11. X = rdm.randn(300,2)
  12. #从X这个300行2列的矩阵中取出一行,判断如果两个坐标的平方和小于2，给Y赋值1，其余赋值0
  13. #作为输入数据集的标签（正确答案）
  14. Y_ = [int(x0*x0 + x1*x1 <2) for (x0,x1) in X]
  15. #遍历Y中的每个元素，1赋值'red'其余赋值'blue'，这样可视化显示时人可以直观区分
  16. Y_c = [['red' if y else 'blue'] for y in Y_]
  17. #对数据集X和标签Y进行shape整理，第一个元素为-1表示，随第二个参数计算得到，第二个元素表示多少列，把X整理为n行2列，把Y整理为n行1列
  18. X = np.vstack(X).reshape(-1,2)#n行两列
  19. Y_ = np.vstack(Y_).reshape(-1,1)
  20. print(X)
  21. print(Y_)
  22. print(Y_c)
  23. #用plt.scatter画出数据集X各行中第0列元素和第1列元素的点即各行的（x0，x1），用各行Y_c对应的值表示颜色（c是color的缩写） 
  24. plt.scatter(X[:,0], X[:,1], c=np.squeeze(Y_c)) 
  25. plt.show()
  28. #定义神经网络的输入、参数和输出，定义前向传播过程 
  29. def get_weight(shape, regularizer):
  30.     w = tf.Variable(tf.random_normal(shape), dtype=tf.float32)
  31.     tf.add_to_collection('losses', tf.contrib.layers.l2_regularizer(regularizer)(w))
  32.     return w
  34. def get_bias(shape):  
  35.     b = tf.Variable(tf.constant(0.01, shape=shape)) 
  36.     return b
  38. x = tf.placeholder(tf.float32, shape=(None, 2))
  39. y_ = tf.placeholder(tf.float32, shape=(None, 1))
  41. w1 = get_weight([2,11], 0.01)    
  42. b1 = get_bias([11])
  43. y1 = tf.nn.relu(tf.matmul(x, w1)+b1)
  45. w2 = get_weight([11,1], 0.01)
  46. b2 = get_bias([1])
  47. y = tf.matmul(y1, w2)+b2 
  50. #定义损失函数
  51. # 一般的损失函数
  52. loss_mse = tf.reduce_mean(tf.square(y-y_))
  53. # 正则化的损失函数
  54. loss_total = loss_mse + tf.add_n(tf.get_collection('losses'))
  57. #定义反向传播方法：不含正则化
  58. train_step = tf.train.AdamOptimizer(0.0001).minimize(loss_mse)
  60. with tf.Session() as sess:
  61.     init_op = tf.global_variables_initializer()
  62.     sess.run(init_op)
  63.     STEPS = 40000
  64.     for i in range(STEPS):
  65.         start = (i*BATCH_SIZE) % 300
  66.         end = start + BATCH_SIZE
  67.         sess.run(train_step, feed_dict={x:X[start:end], y_:Y_[start:end]})
  68.         if i % 2000 == 0:
  69.             loss_mse_v = sess.run(loss_mse, feed_dict={x:X, y_:Y_})
  70.             print("After %d steps, loss is: %f" %(i, loss_mse_v))
  71.     #xx在-3到3之间以步长为0.01，yy在-3到3之间以步长0.01,生成二维网格坐标点
  72.     xx, yy = np.mgrid[-3:3:.01, -3:3:.01]
  73.     #将xx , yy拉直，并合并成一个2列的矩阵，得到一个网格坐标点的集合
  74.     grid = np.c_[xx.ravel(), yy.ravel()]
  75.     #将网格坐标点喂入神经网络 ，probs为输出
  76.     probs = sess.run(y, feed_dict={x:grid})
  77.     #probs的shape调整成xx的样子
  78.     probs = probs.reshape(xx.shape)
  79.     print("w1:\n",sess.run(w1))
  80.     print("b1:\n",sess.run(b1))
  81.     print("w2:\n",sess.run(w2))
  82.     print("b2:\n",sess.run(b2))
  84. plt.scatter(X[:,0], X[:,1], c=np.squeeze(Y_c))
  85. plt.contour(xx, yy, probs, levels=[.5])
  86. plt.show()
  90. #定义反向传播方法：包含正则化
  91. train_step = tf.train.AdamOptimizer(0.0001).minimize(loss_total)
  93. with tf.Session() as sess:
  94.     init_op = tf.global_variables_initializer()
  95.     sess.run(init_op)
  96.     STEPS = 40000
  97.     for i in range(STEPS):
  98.         start = (i*BATCH_SIZE) % 300
  99.         end = start + BATCH_SIZE
  100.         sess.run(train_step, feed_dict={x: X[start:end], y_:Y_[start:end]})
  101.         if i % 2000 == 0:
  102.             loss_v = sess.run(loss_total, feed_dict={x:X,y_:Y_})
  103.             print("After %d steps, loss is: %f" %(i, loss_v))
  105.     xx, yy = np.mgrid[-3:3:.01, -3:3:.01]
  106.     grid = np.c_[xx.ravel(), yy.ravel()]
  107.     probs = sess.run(y, feed_dict={x:grid})
  108.     probs = probs.reshape(xx.shape)
  109.     print("w1:\n",sess.run(w1))
  110.     print("b1:\n",sess.run(b1))
  111.     print("w2:\n",sess.run(w2))
  112.     print("b2:\n",sess.run(b2))
  114. plt.scatter(X[:,0], X[:,1], c=np.squeeze(Y_c)) 
  115. plt.contour(xx, yy, probs, levels=[.5])
  116. plt.show()

左边是没有正则化，右边是正则化的结果
截屏2020-12-19 下午8.50.21.png