目录

1 简介

K-均值（K-means）是一种分区聚类。将数据分为不重叠的子集（簇），而没有任何簇的内部结构或标签。是一种无监督学习算法（divides the data into non-overlapping subsets (clusters) without any cluster internal strcture）在簇内是非常相似的，在簇外是非常不同的。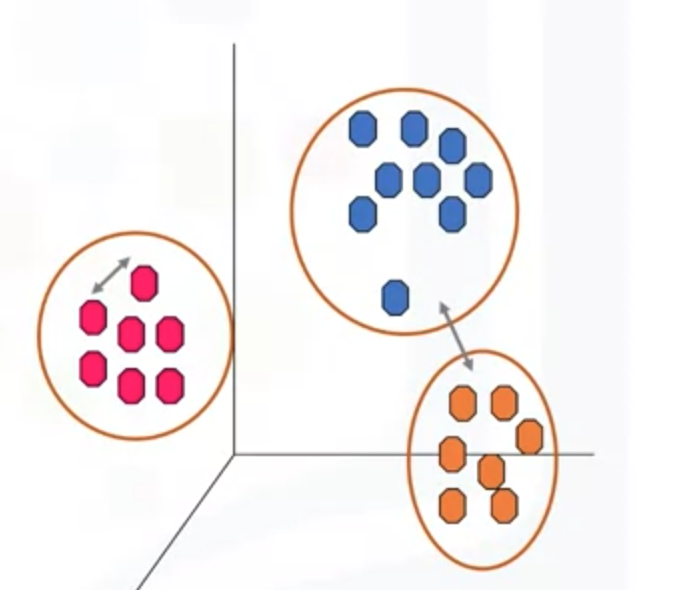

2 计算相似度和非相似度

K-means 本质上是努力最小化簇内距离，最大化簇间距离；以类似的样本进入一个簇，而不同的样本进入不同的簇的方式形成簇群；将数据分为不重叠的子集（簇），而没有任何簇的内部结构或标签。
以下举例多维相似度的计算

3 K-均值聚类的算法过程

举例说明：假设簇只有两个特征，age 和income

散点图表示客户的分布，y表示年龄，x表示收入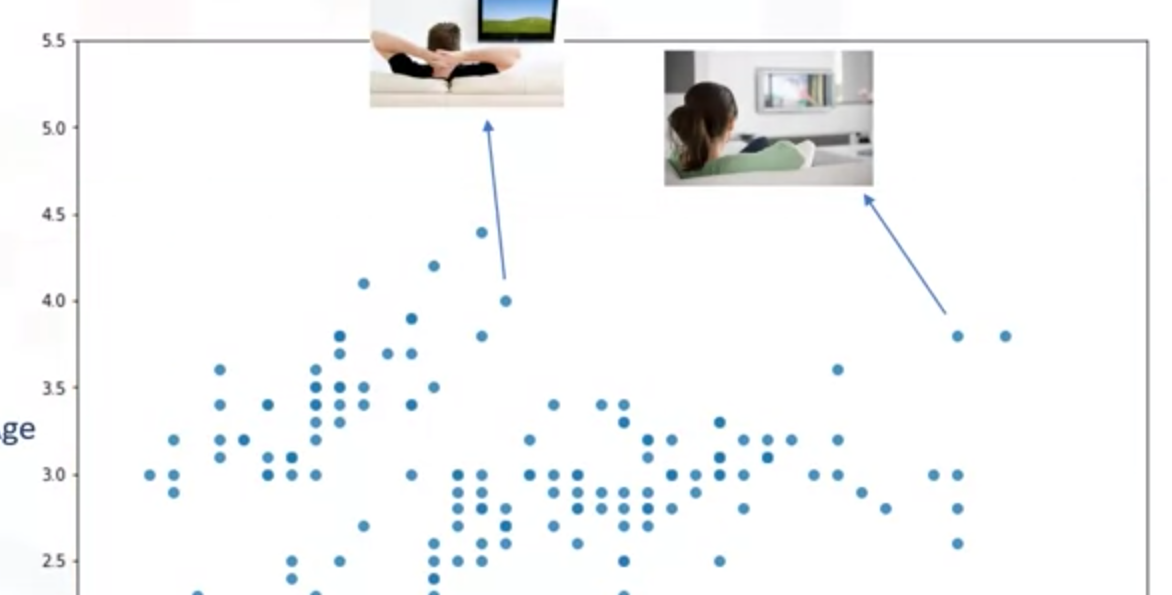

我们的目标：把数据集点分成几个簇，如下所示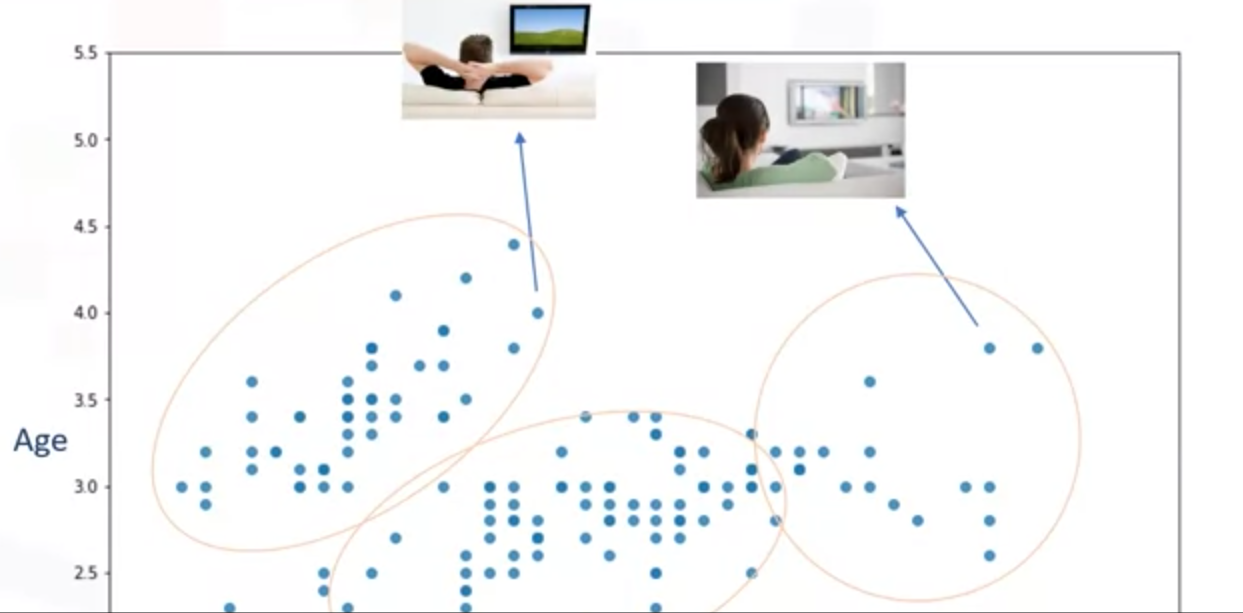

（1）初始化k，随机选择k个中心点

（2）计算距离（相似度）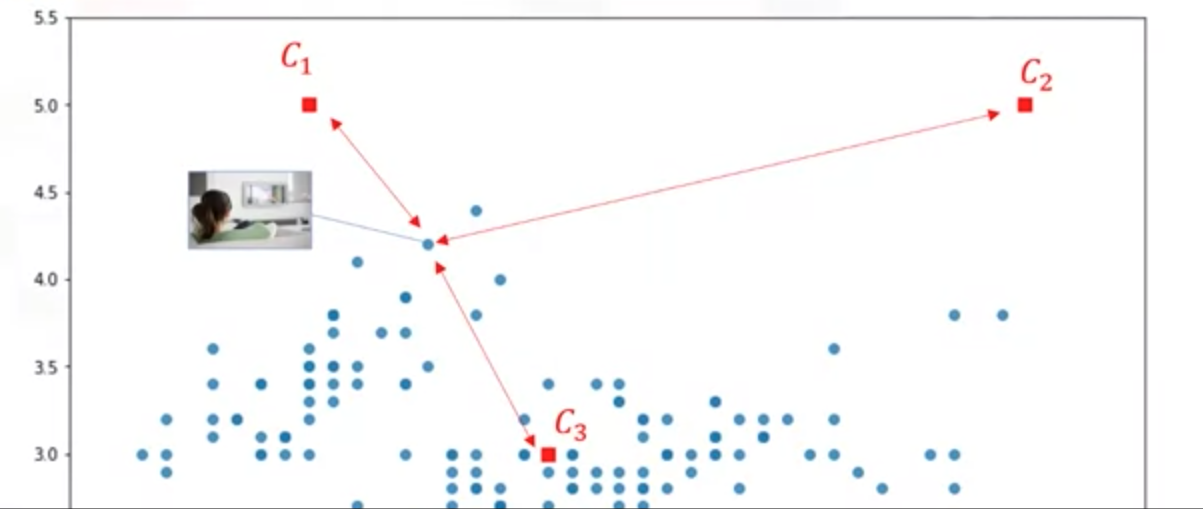

（3）将每个点分配给最近的点（centroid）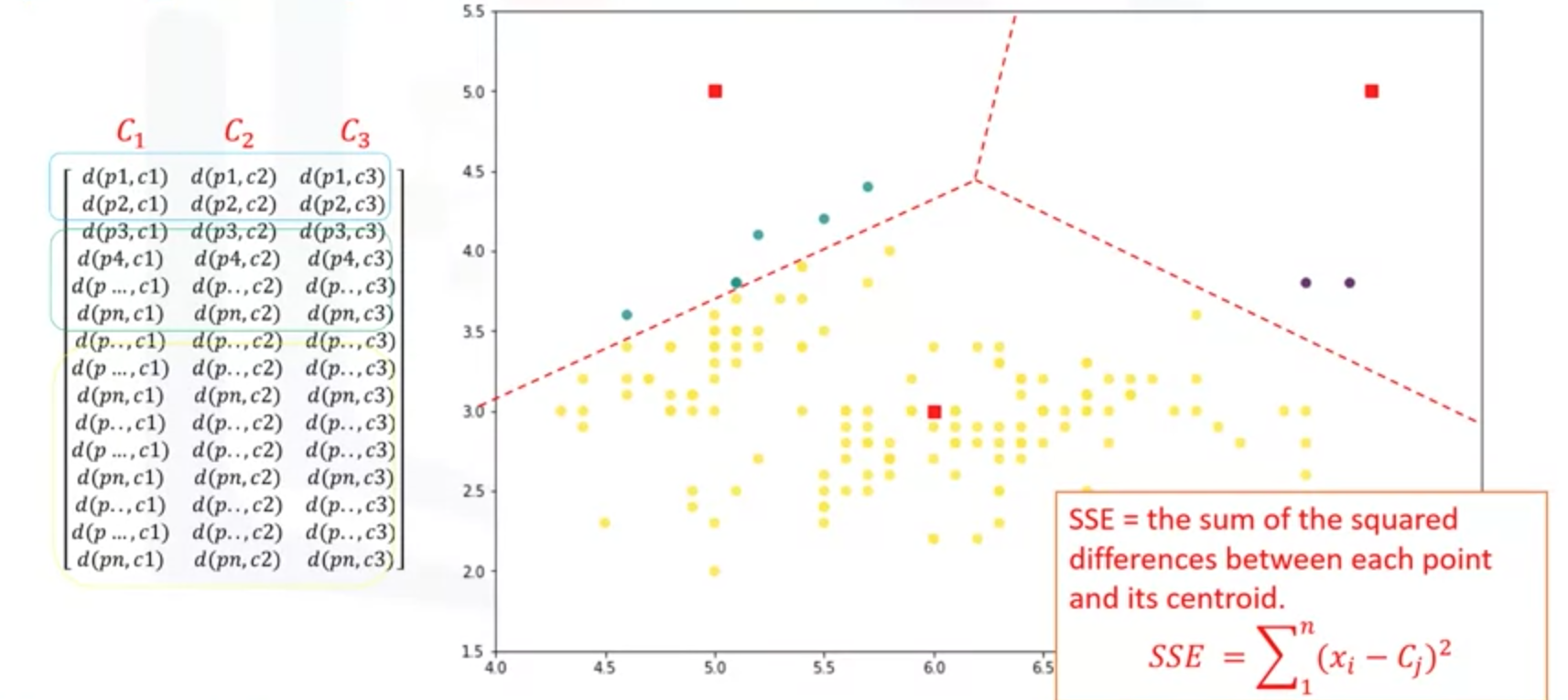

（4）为每个簇计算新的点

（5）重复直到不再有改变

4 K-均值算法步骤

（1）对每个簇随意放置K重心值
（2）计算所有点和这个重点的距离
（3）为每个数据点分配最近的重心点，创建一个簇
（4）重新计算k重心的位置
（5）重复第2-4步，直到重心点不再移动

5 K-均值准确率

如何评估由K-均值算法形成的簇的好坏?即是计算簇的准确率？
（1）外部方法
如果可以，把簇和真实的数据进行比较（一般不可能）
（2）内部方法
平均数据点和簇之间的距离

6 选择K值

计算不同k值下的数据点和簇的重心点之间距离的平均值。选择在肘点的K值作为初始值

7 K-均值特点

（1）是一种基于分类的算法，在中型和大型数据中相对有效
（2）产生球状簇
（3）缺点是需要提前分类簇的数量