1 基本概念

（1）1943年McCulloch Pitts提出的神经元模型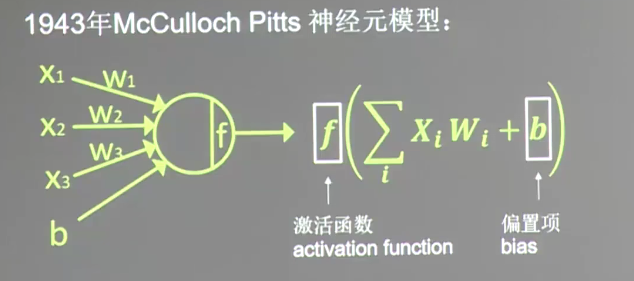

（2）常用的激活函数

• relu
• sigmoid
• tanh

（3）神经网络的复杂度
多用NN层数和NN参数的个数表示

网络的层数 = 隐藏层的层数+1个输出层
网络的总参数 =总的权重+ 总的偏执

2 损失函数

（1）损失函数（loss）：预测值(y)与已知答案（y_）的差距
（2）均方误差MSE

loss = tf.reducemean(tf.square(y-y))

（3）代码举例讲解
预测酸奶日销量y。x1 x2是影响日销量的因素。
建模前，应预先采集的数据有：每日x1 x2 和销量y(即已经答案，最佳情况，产量=销量)
拟造数据集X,Y ;y =x1+ x2
噪声：-0.05~+0.05 ，拟合可以预测销量的函数

#coding:utf-8
#预测多或预测少的影响一样
#0导入模块，生成数据集
import tensorflow as tf
import numpy as np
BATCH_SIZE = 8
SEED = 23455
rdm = np.random.RandomState(SEED)#基于seed产生随机数
X = rdm.rand(32,2)#随机数返回300行2列的矩阵，表示300组坐标点.数据集
Y_ = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X]#判断如果两个坐标的平方和小于2，给Y赋值1，其余赋值0；标签集
#1定义神经网络的输入、参数和输出，定义前向传播过程。
x = tf.placeholder(tf.float32, shape=(None, 2))#占位
y_ = tf.placeholder(tf.float32, shape=(None, 1))#占位
w1= tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))#正态分布
y = tf.matmul(x, w1)#点积
#2定义损失函数及反向传播方法。
#定义损失函数为MSE,反向传播方法为梯度下降。
loss_mse = tf.reduce_mean(tf.square(y_ - y))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss_mse)
#3生成会话，训练STEPS轮
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()#初始化
    sess.run(init_op)#初始化
    STEPS = 20000#20000轮
    for i in range(STEPS):
        start = (i*BATCH_SIZE) % 32
        end = (i*BATCH_SIZE) % 32 + BATCH_SIZE
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y_[start:end]})
        if i % 500 == 0:
            print ("After %d training steps, w1 is: " % (i))
            print (sess.run(w1), "\n")
    print ("Final w1 is: \n", sess.run(w1))
#在本代码#2中尝试其他反向传播方法，看对收敛速度的影响，把体会写到笔记中

3 自定义损失函数

代码实现以上的公式

loss =tf.reduce_sum(tf.where(tf.greater(y,y_),COST(y-y_),PROFIT(y_-y)))# 分段函数，倒数第二个参数是真值时执行，导数第一个是假值时执行

预测酸奶销量，酸奶成本（COST）为1元，酸奶利润（FROFIT）为9元。
预测少了损失利润9元，大于预测多了损失成本1元
预测少了损失大，希望生成的预测函数往多了预测。

#酸奶成本1元， 酸奶利润9元
#预测少了损失大，故不要预测少，故生成的模型会多预测一些
#0导入模块，生成数据集
import tensorflow as tf
import numpy as np
BATCH_SIZE = 8
SEED = 23455#随机种子
COST = 1#花费
PROFIT = 9#成本
rdm = np.random.RandomState(SEED)#基于seed产生随机数
X = rdm.rand(32,2)#随机数返回32行2列的矩阵 表示32组 体积和重量 作为输入数据集
Y = [[x1+x2+(rdm.rand()/10.0-0.05)] for (x1, x2) in X]
#1定义神经网络的输入、参数和输出，定义前向传播过程。
x = tf.placeholder(tf.float32, shape=(None, 2))#占位
y_ = tf.placeholder(tf.float32, shape=(None, 1))#占位
w1= tf.Variable(tf.random_normal([2, 1], stddev=1, seed=1))#正态分布
y = tf.matmul(x, w1)#点积
#2定义损失函数及反向传播方法。
# 定义损失函数使得预测少了的损失大，于是模型应该偏向多的方向预测。
#tf.where:如果condition对应位置值为True那么返回Tensor对应位置为x的值，否则为y的值.
#where(condition, x=None, y=None,name=None)
loss = tf.reduce_sum(tf.where(tf.greater(y, y_), (y - y_)*COST, (y_ - y)*PROFIT))
train_step = tf.train.GradientDescentOptimizer(0.001).minimize(loss)#随机梯度下降
#3生成会话，训练STEPS轮。
with tf.Session() as sess:
    init_op = tf.global_variables_initializer()#初始化
    sess.run(init_op)#初始化
    STEPS = 3000
    for i in range(STEPS):#三千轮
        start = (i*BATCH_SIZE) % 32  #8个数据  为一个数据块输出
        end = (i*BATCH_SIZE) % 32 + BATCH_SIZE  #[i:i+8]
        sess.run(train_step, feed_dict={x: X[start:end], y_: Y[start:end]})#训练
        if i % 500 == 0:#每500轮打印输出
            print("After %d training steps, w1 is: " % (i))#打印i
            print(sess.run(w1), "\n")#打印w1
    print("Final w1 is: \n", sess.run(w1))#最终打印w1

4 交叉熵(Cross Entropy)

交叉熵：表征两个概率分布之前的距离。

ce = -tf.reducemean(y*tf.log(tf.clip_by_calue(y,1e-2,1.0)))

可以以下用Softmax的方法替换该交叉熵的方法。

ce = tf.nn.sparsesoftmax_cross_entropy_with_logits(logits=y,labels =tf.argmax(y,1)) cem =tf.reduce_mean(ce)