目录

1 简介

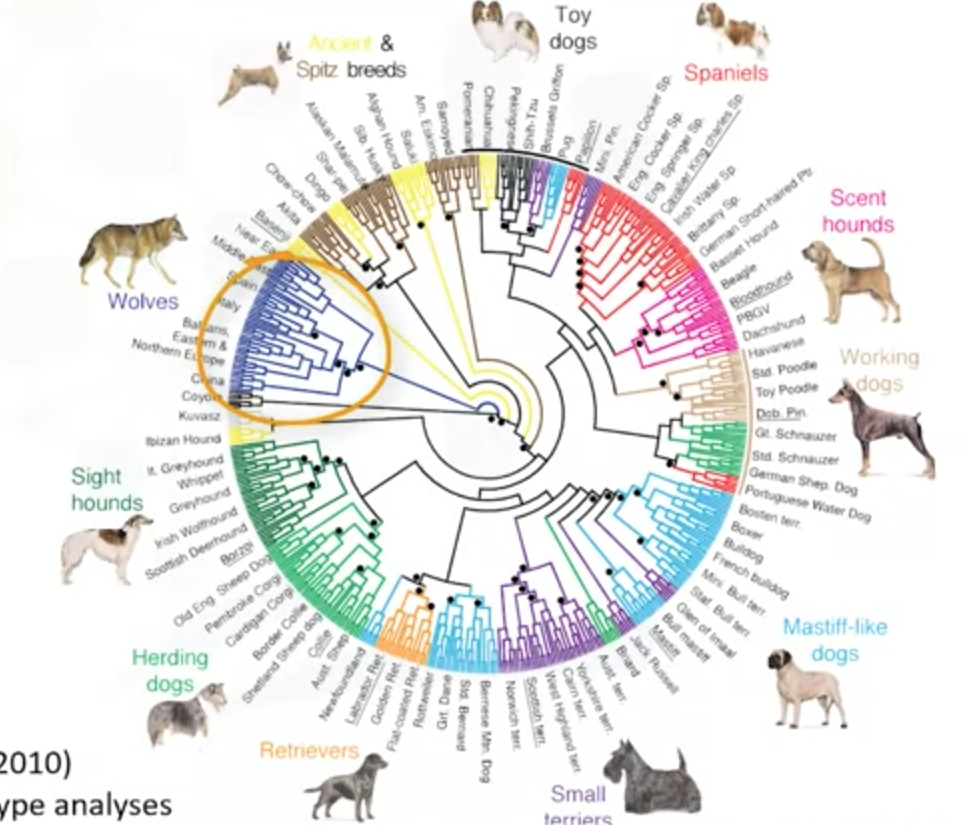
层次聚类算法是建立簇的层次，每个结点是一个簇，且又包含了子簇结点。层次聚类算法包括聚集聚类算法和分裂聚集算法。分裂聚集是从一个大的簇划分为小的结点。而聚集聚类是反过来的，从单个结点到一个大的簇。

2 举例介绍聚集聚类

吴恩达老师特别形象的用以下计算几个地方的最佳距离之和的例子，说明了聚集聚类的算法过程。
（1）根据计算点与点之间的具体，做成一个表格。以下中的OT-MO的距离最短，只有167.那就以这两个结点作为树的结点。类似数据结构中生成哈夫曼树的过程。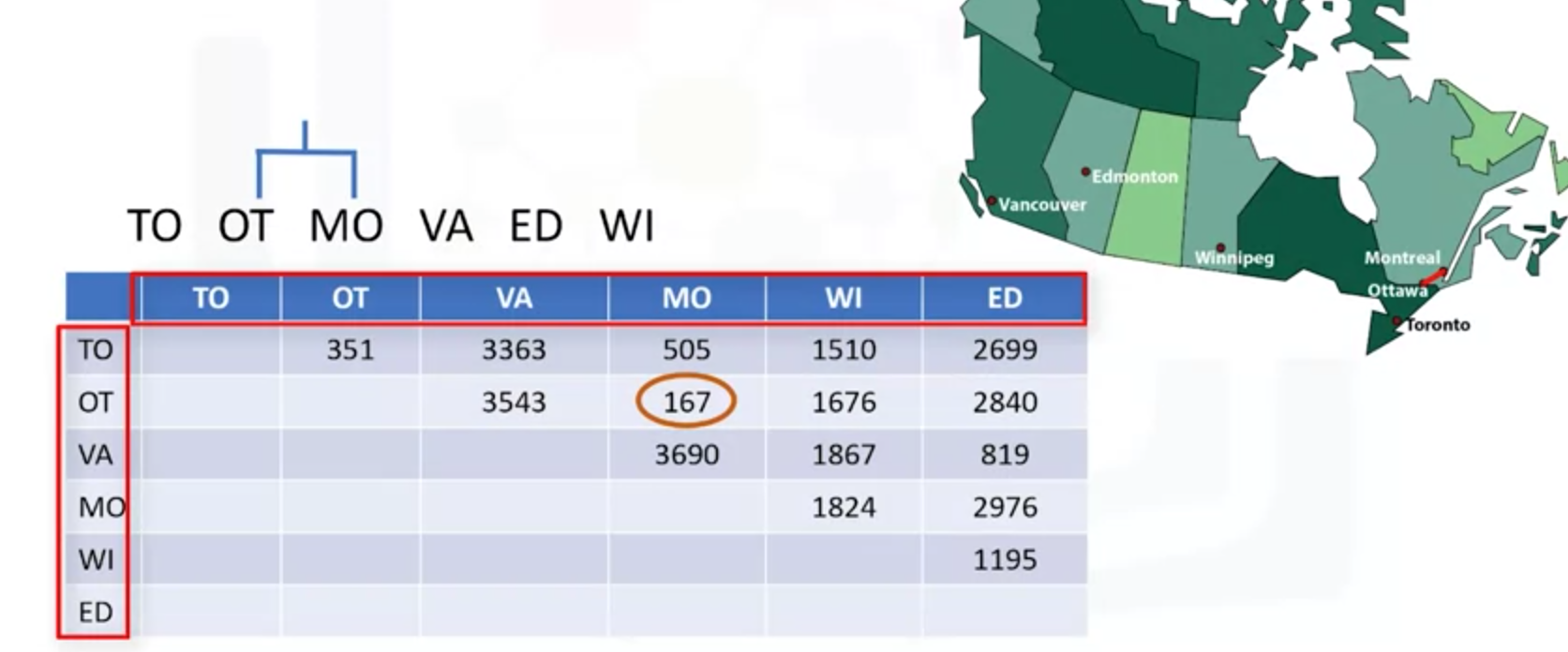

（2）然后合并两个点，取两个点连线的中间，作为一个新的生成点，重新计算距离，做成表格。

（3）在表格中选择最小值的两个点进行两两合并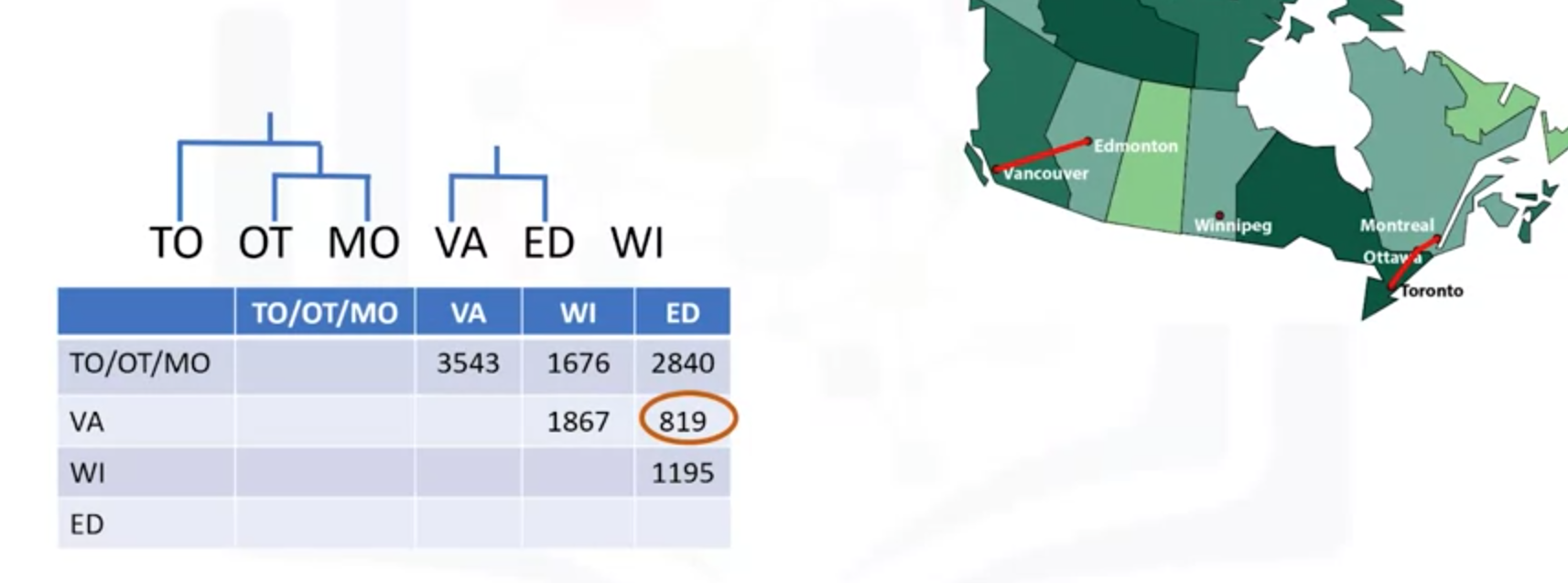

（4）同理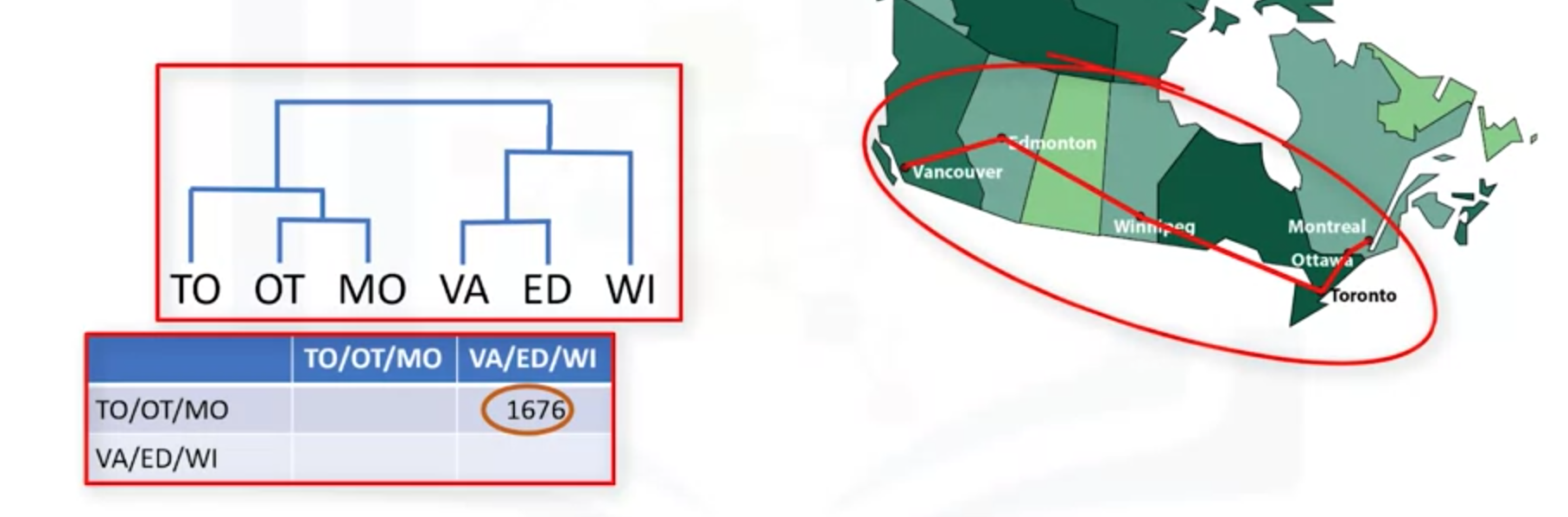

（5）可以用树状图表示，纵坐标y轴表示两个簇之间的相似度。随便划一条横线，穿过的三条线，此时这条线的y值表示这三个点的相似度。

3 聚集算法

（1）创建n个簇，一个簇对应一个数据点
（2）计算邻近矩阵
（3）循环以下步骤

• 合并两个最近的簇
• 更新邻近矩阵(proximity matrix)

（4）直到只有一个簇

4 簇之间的相似度/距离

（1）单链聚类Singl-Linkage Clustering
簇之间的最小距离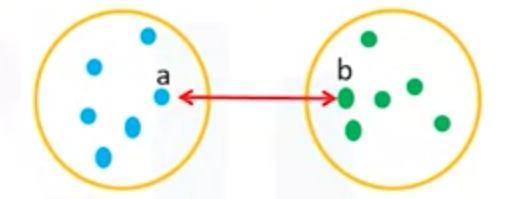

（2）竞争类聚类Complete-Linkag Clustering
簇之间的最大距离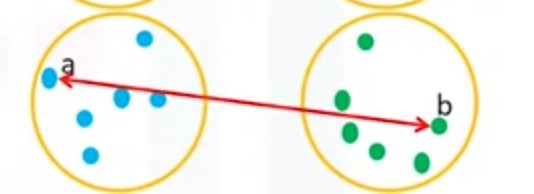

（3）平均连锁聚类Average Linkage Clustering
簇之间的平均距离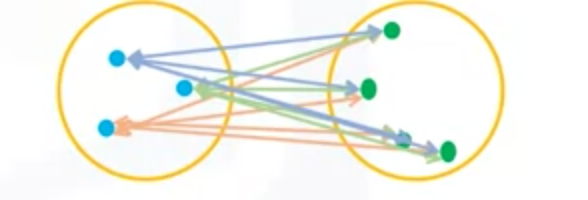

（4）重心链接聚类Centroid Linkage Cluster
簇的重心之间的距离

5 层次聚类的优缺点

（1）优点

• 不需要制定簇的数量
• 容易实施
• 产生树状图帮助理解

（2）缺点

• 不能撤销之前的任何步骤：比如当前聚类连接了两个点，后面又发现了更好的两个点，但是此时程序不能撤销该步骤
• 与K-均值算法相比会有更长的运行时间
• 数据集很大时候，有时不能通过树状图去计算正确的簇的数量

6 K-均值VS层次聚类