105. 从前序与中序遍历序列构造二叉树

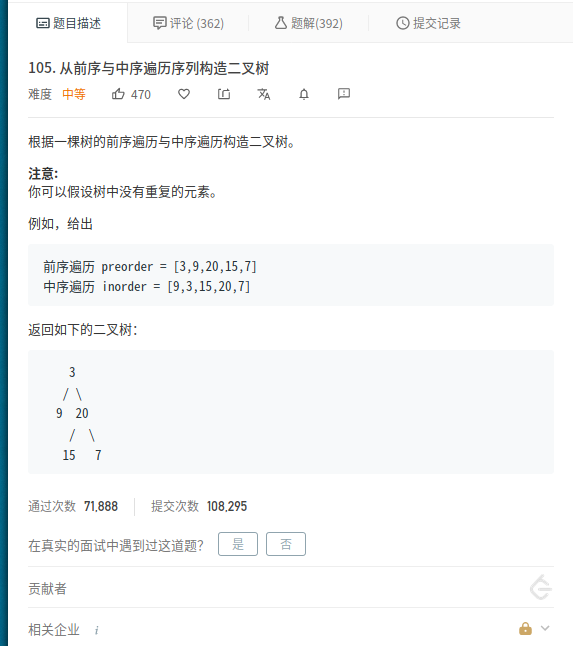
105. 从前序与中序遍历序列构造二叉树

解题的核心是查找前序遍历和中序遍历中的根节点，左节点，右节点 三者之前的边界点， 不要看给的数据例子 把当前问题缩小例如就三个数 前序【3,9,20】 中序【9，3，20】，递归本身就是把大问题化解成相同的小问题，然后用小问题的解来处理大问题的解。
1 前序遍历是 1根节点 2 左节点 3 右节点
2 中序遍历是 1左节点 2根节点 3右节点
3 前序遍历可以确定根节点是前序数组的第一个数preorder[0]
4 查找中序遍历左右节点的边界，中序遍历根节点的位置inorder[1] ，可以发现 inorder[1]左边都是树左节点的，左节点个数是1个，即[9]，inorder[1]右边都是树右节点的，右节点的个数也是1，即[20]，
5 查找前序遍历左右节点的边界，前序遍历第一个节点是根节点，然后依次是左节点和右节点，而我们中序遍历不仅知道左节点的和右节点，实际上根据根节点的索引值也表示出了左节点和右节点个数，根节点索引值i是1，所以preorder[i:i+1]即[9] ,而preorder[i+1:]就是右节点,即[20]。
6 总结 边界索引里的中序遍历的根节点位置，即是表示出了根节点索引也是左节点的个数。

package main
import "fmt"
type TreeNode struct {
    Val   int
    Left  *TreeNode
    Right *TreeNode
}
func buildTree(preorder []int, inorder []int) *TreeNode {
    if len(preorder) == 0 {
        return nil
    }
    rootVal := preorder[0]
    i := 0
    // 查找根节点位置
    for ; i < len(inorder); i++ {
        if rootVal == inorder[i] {
            break
        }
    }
    root := &TreeNode{Val: rootVal}
    root.Left = buildTree(preorder[1:i+1], inorder[:i])
    root.Right = buildTree(preorder[i+1:], inorder[i+1:])
    return root
}
func main() {
    r := buildTree([]int{3, 9, 20, 15, 7}, []int{9, 3, 15, 20, 7})
    printPreorder(r)
    fmt.Println()
    printInorder(r)
}
func printPreorder(r *TreeNode) {
    if r == nil {
        return
    }
    fmt.Print(r.Val)
    printPreorder(r.Left)
    printPreorder(r.Right)
}
func printInorder(r *TreeNode) {
    if r == nil {
        return
    }
    printInorder(r.Left)
    fmt.Print(r.Val)
    printInorder(r.Right)
}