概念
树(英语:tree)是一种抽象数据类型(ADT)或是实现这种抽象数据类型的数据结构,用来模拟具有树状结构性质的数据集合。它是由n(n>0)个有限节点组成一个具有层次关系的集合。把它叫做“树”是因为它看起来像一棵倒挂的树,也就是说它是根朝上,而叶朝下的。
特点
- 只有一个根节点,没有父节点的节点称为根节点;
- 每一个非根节点有且只有一个父节点;
- 每个节点都只有有限个子节点或无子节点;
- 除了根节点外,每个子节点可以分为多个不相交的子树;
- 树里面没有环路(cycle)
术语
树(tree)是被称为结点(node)的实体的集合。结点通过边(edge)连接。每个结点都包含值或数据(value/date),并且每结节点可能有也可能没有子结点。
| 术语 | 说明 |
|---|---|
| 结点(node) | 树中存储 数据元素以及 结点之间的逻辑连接信息的数据。一般使用一个圆圈表示。 |
| 根结点 | 树的首结点,即root结点,树的逻辑形态的最顶层,它没有父结点。 |
| 节点的度 | 一个节点含有的子树的个数称 |
| 树的度 | 一棵树中,最大的节点度称为树的度 |
| 叶子结点(leaf) | 度为零的节点; |
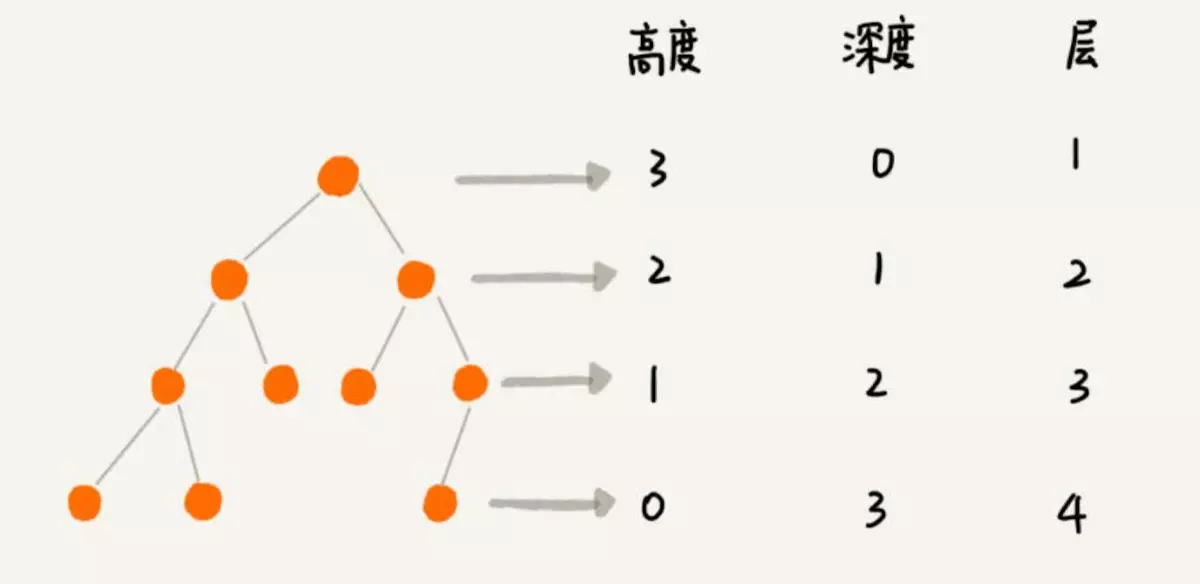
| 高度Height | 节点到叶子节点的最长路径,树的高度等于根节点的高度。 |
| 深度Depth | 根节点到这个节点的所尽力的边的个数 |
| 层Level | 节点的深度+1 |
| 父节点 | 若一个节点含有子节点,则这个节点称为其子节点的父节点; |
| 叶子结点 | 是树的末端结点,他们没有子结点, |
| 兄弟节点 | 由一个父节点衍生出来的节点 |
天然的组织结构
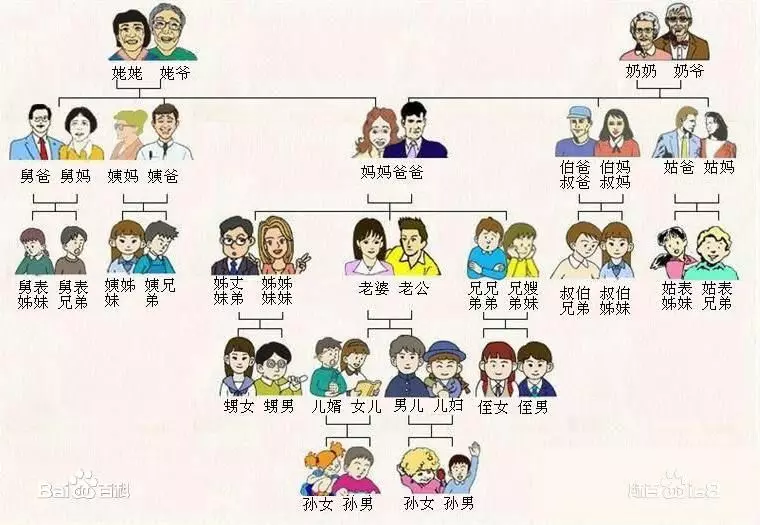
家族关系
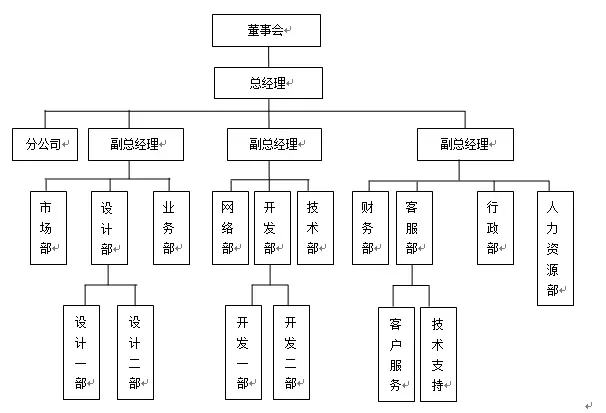
组织结构
HTML
在 HTML 中,文档对象模型(DOM)是树形结构的。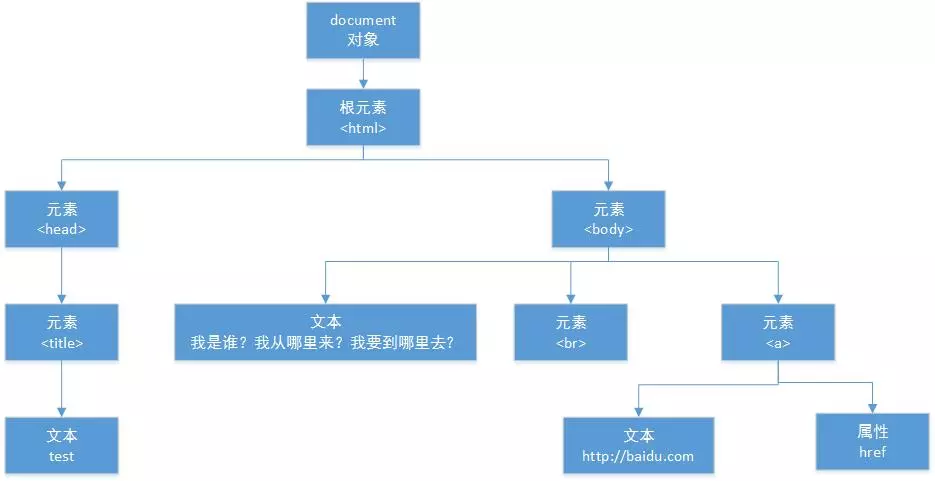
解决的问题
高效

这个索引可以把原本O(n)的查找操作变为O(logn),可以简单地理解为在数据结构的层面上构造了一个二分查找算法。总之,树通过其结构来表达了一种划分查找方法,这一方法相比于遍历搜索的复杂度O(n),一般情况下复杂度仅有O(logn)。
稳定
如果我们仅仅考虑效率问题,那散列比树要屌的多。查找复杂度为O(1)。之所以不能用散列来取代树,是因为散列需要预先开辟大量空间,并不是所有场景下都可以这么做;而如果空间不够,则会出现散列冲突(索引结构被破坏)。树则可以动态改变存储空间,且运用一些手段来保护自身索引结构。
自平衡二叉搜索树 (self-balanced BST)的精髓,便在于其维护自身稳定(平衡)的能力。当树不平衡时,其搜索复杂度便不再是O(logn)了——考虑一个极端情况:一棵树每个节点都只有右子节点,那么树就退化为了链表,查找复杂度也和链表一样是O(n):
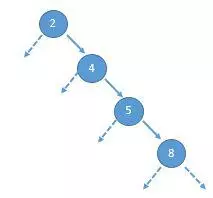
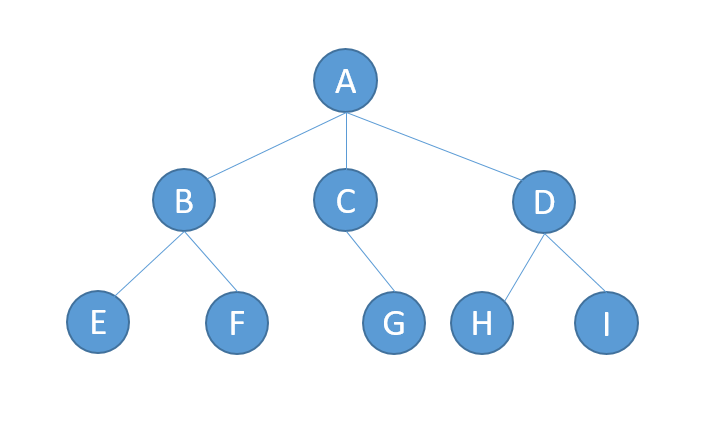
树结构表示
python实现
class TreeNode:def __init__(self,val):self.val = valself.left,self.right = None,None
Java实现
public class TreeNode {public int val;public TreeNode left,right;public TreeNode(int val){this.left = null;this.right = null;this.val = val;}}
顺序存储
树的顺序存储结构中最简单直观的就是用一维数组表示的双亲存储结构。如下图所示: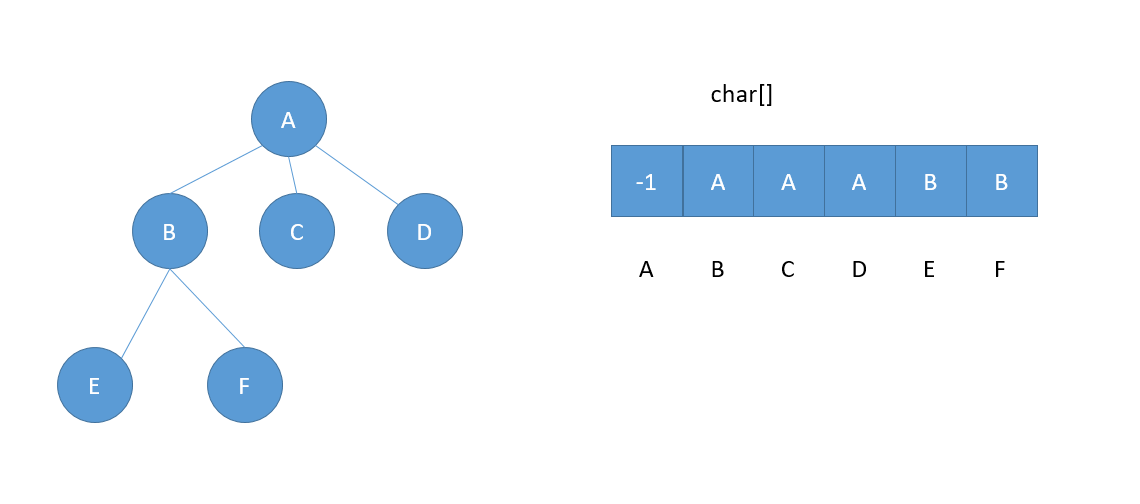
用char[]来存储树的双亲关系,将对应的树的结点的内容映射为数组的下标,图中直接用字符表示。内容就是该结点的双亲结点。
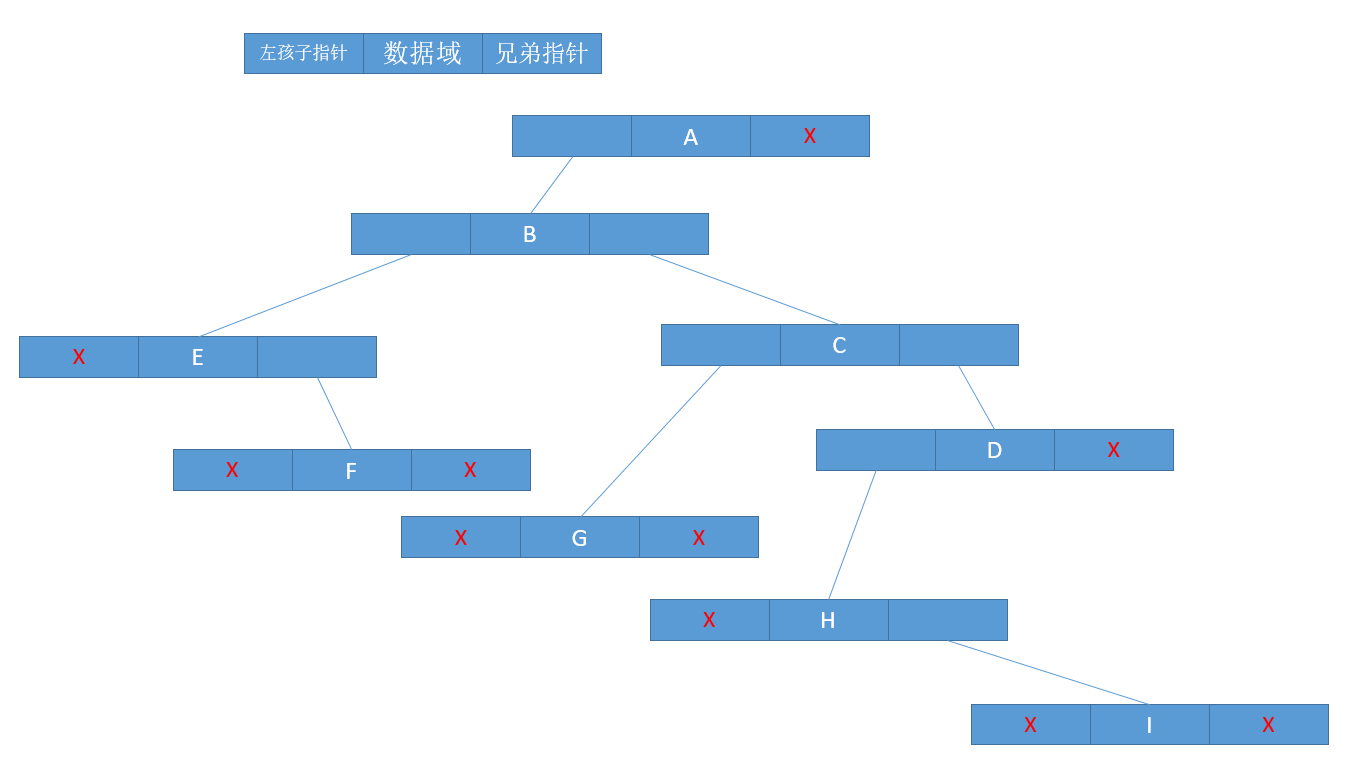
链式存储
参考
https://segmentfault.com/a/1190000019240488?utm_source=tag-newest