5. 最长回文子串

状态定义

dp[l,r]：字符串s从索引l到r的子串是否是回文串
true： s[l,r] 是回文串
false：s[l,r] 不是回文串

状态转移

dp[l][r] = dp[l+1][r-1] && s[l] == s[r]
s[l] == s[r]：说明当前中心可以继续扩张，进而有可能扩大回文串的长度
dp[l+1][r-1]：true
说明s[l,r]的子串s[l+1][r-1]也是回文串

边界处理

l - r <= 2：2表示aba类型；1表示aa类型；0表示a类型 这些只需要判断s[l]==s[r]就可以了
总结
dp[l][r] = s[l] == s[r] && ( r - l <= 2&&dp[l+1][r-1])

从头部开始遍历

func longestPalindrome(s string) string {
    if len(s)<2 {
        return s
    }
    dp :=make([][]bool,len(s))
    for i:=range s{
        dp[i] = make([]bool,len(s))
    }
    result := string(s[0])
    for r:=0;r<len(s);r++{
        for l:=0;l<=r;l++{
            if s[l]==s[r]&&(r-l<=2||dp[l+1][r-1]){
                dp[l][r]= true
                if len(s[l:r+1])>len(result){
                    result =s[l:r+1]
                }
            }
        }
    }
    return result
}

从尾部开始遍历

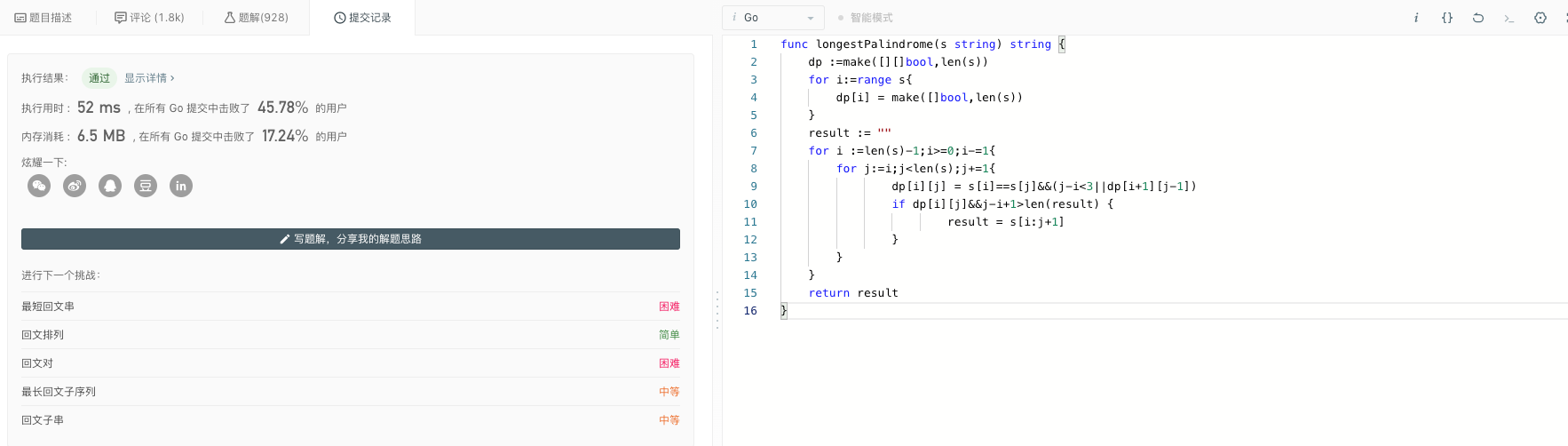
package main
import "fmt"
// 动态规划
func longestPalindrome(s string) string {
    dp :=make([][]bool,len(s))
    for i:=range s{
        dp[i] = make([]bool,len(s))
    }
    result := ""
    for i :=len(s)-1;i>=0;i-=1{
        for j:=i;j<len(s);j+=1{
                dp[i][j] = s[i]==s[j]&&(j-i<3||dp[i+1][j-1])
                if dp[i][j]&&j-i+1>len(result) {
                        result = s[i:j+1]
                }
        }
    }
    return result
}
func main() {
    fmt.Println(longestPalindrome("babad"))
}

func longestPalindrome(s string) string {
    lenth := len(s)
    if lenth <= 1 {
        return s
    }
    dp := make([][]bool, lenth)
    start := 0
    max := 1
    for r := 0;r<lenth;r++ {
        dp[r] = make([]bool, lenth)
        for l:=0;l<r;l++ {
            dp[l][r]= s[l] == s[r] && (r -l <= 2 || dp[l+1][r-1])
            if dp[l][r] {
                curr := r-l+1
                if curr > max {
                    max = curr
                    start = l
                }
            }
        }
    }
    return s[start:start+max]
}