543. 二叉树的直径

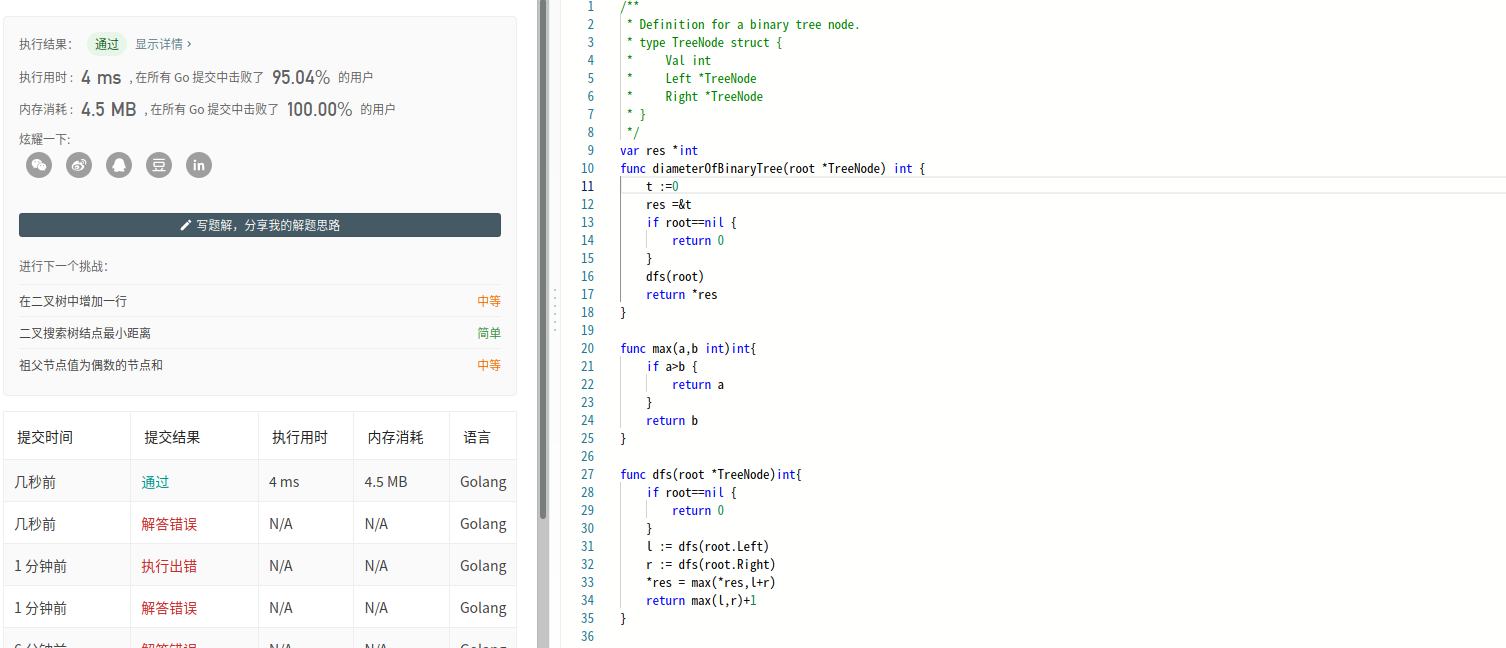
package main
import "fmt"
type TreeNode struct {
    Val int
    Left *TreeNode
    Right *TreeNode
}
var res *int // leetcode bug 全局变量最好是指针
func diameterOfBinaryTree(root *TreeNode) int {
    t :=1
    res =&t
    if root==nil {
        return 0
    }
    dfs(root)
    return *res
}
func max(a,b int)int{
    if a>b {
        return a
    }
    return b
}
func dfs(root *TreeNode)int{
    if root==nil {
        return 0
    }
    l := dfs(root.Left)
    r := dfs(root.Right)
    *res = max(*res,l+r)
    return max(l,r)+1
}
func main() {
    a := &TreeNode{
        Val: 1,
    }
    b := &TreeNode{
        Val: 2,
    }
    a.Left = b
    c := &TreeNode{
        Val: 3,
    }
    a.Right = c
    d := &TreeNode{
        Val: 4,
    }
    b.Left = d
    e := &TreeNode{
        Val: 5,
    }
    b.Right = e
    fmt.Println(diameterOfBinaryTree(a))
    g := &TreeNode{
        Val: 1,
    }
    fmt.Println(diameterOfBinaryTree(g))
}

class Solution {
    /**
     * 思路：根据题目意思，就是找左右子树的最大深度，最大深度的两个节点之间的距离就是直径，那也就是变成我们要去找左右子树的最大深度问题，
     * 起初我的实现只认为以入参的根节点为基准找左右子树的最大深度然后进行相加就是直径，但是发现可能存在不一定是以根节点为基准得到直径是最大的，
     * 也可能是在子树当中
     * 所以实现过程中用一个全局变量res来记录在获取所有节点的最大深度时先处理看是否以当前节点为根节点得到的直径是否是最大的，是的话就维系一下最大值
     */
    private int res = 0; // 用来记录以某个节点为根节点的时候，最大的路径
    public int diameterOfBinaryTree(TreeNode root) {
        if (root == null) return 0;
        getMaxDep(root);
        return res;
    }
    private int getMaxDep(TreeNode curRoot){
        if (curRoot == null) return 0;
        //if (curRoot.left == null && curRoot.right == null) return 1;
        int leftDep = getMaxDep(curRoot.left); // 原本这里要+1
        int rightDep = getMaxDep(curRoot.right); // 这里也要+1
        if ((leftDep + rightDep) > res) res = leftDep + rightDep; // 原本这里leftDep + rightDep 还要-2，但是和上面的抵消了，就最后写成这样
        return Math.max(leftDep, rightDep) + 1; // 返回当前根节点的最大深度
    }
}

或者

// 当前节点左子树的深度与右子树的深度之和即为以当前节点为根的二叉树的最长路径
// 两次递归中序遍历嵌套，一次为求以每个节点为根的数的深度，一次为求以每个节点为根的最长路径
// 时间复杂度：O(n^2)  空间复杂度：O(h^2)  h为树的高度，每一层递归都需要分配栈空间，每一层中分配的空间为常数
var max_path int  // 通过全局变量记录最长路径
func diameterOfBinaryTree(root *TreeNode) int {
    max_path = 0  // 刷新全局变量
    getDiameterOfBinaryTree(root)
    return max_path        
}
// 递归中序遍历每个节点，计算以该节点为根节点的最长路径，比较所有节点的最长路径获取整棵树的最长路径
func getDiameterOfBinaryTree(root *TreeNode) {
    if root==nil {
        return
    }
    // 当前节点左子树的深度与右子树的深度之和即为以当前节点为根的二叉树的最长路径
    path := getDepthOfBinaryTree(root.Left) + getDepthOfBinaryTree(root.Right)
    if path>max_path {
        max_path = path
    }
    getDiameterOfBinaryTree(root.Left)
    getDiameterOfBinaryTree(root.Right)
}
// 计算以当前节点为根节点的树的深度
func getDepthOfBinaryTree(root *TreeNode) int {
    if root==nil {
        return 0
    }
    return int(math.Max(float64(getDepthOfBinaryTree(root.Left)), 
    float64(getDepthOfBinaryTree(root.Right)))) + 1
}