概述
二叉树是树的一种特殊形式,‘二’意味着每个结点最多有2个的子节点树(tree。除了根节点以外每个节点都只有一个父亲节点
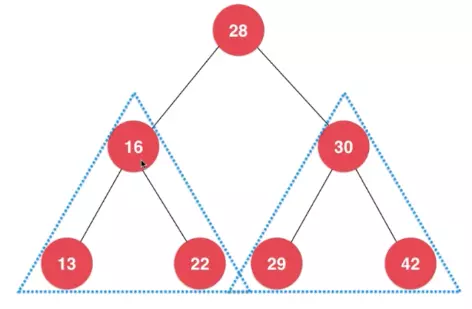
二叉树的节点的两个孩子节点,左边的子节点称为左孩子,右边的子节点称为右孩子,具体类表示为如下
class Node {E e;Node left;Node right;}
根据左右子树特点,分为以下特殊的二叉树
| 分类 | 说明 |
|---|---|
| 满二叉树 | 一个二叉树所有非叶子节点都存在左右子树,并且所有的叶子节点都在同一层级上 |
| 完全二叉树 | 和满二叉树类似,区别在与最底层,也就是叶子节点那一层,叶子节点从左到友依次排列,不需要填满二叉树 |
| 平衡二叉树 | 左右子树的高度差至多为1,也就是说任何节点的左子树的叶子节点到节点的最长距离,不能超过右子树的叶子节点到节点的最长距离+1 |
验证二叉搜索树
https://leetcode-cn.com/problems/validate-binary-search-tree/
递归
class Solution {public boolean helper(TreeNode node, Integer lower, Integer upper) {if (node == null) return true;int val = node.val;if (lower != null && val <= lower) return false;if (upper != null && val >= upper) return false;if (! helper(node.right, val, upper)) return false;if (! helper(node.left, lower, val)) return false;return true;}public boolean isValidBST(TreeNode root) {return helper(root, null, null);}}
复杂度分析
class Solution {LinkedList<TreeNode> stack = new LinkedList();LinkedList<Integer> uppers = new LinkedList(),lowers = new LinkedList();public void update(TreeNode root, Integer lower, Integer upper) {stack.add(root);lowers.add(lower);uppers.add(upper);}public boolean isValidBST(TreeNode root) {Integer lower = null, upper = null, val;update(root, lower, upper);while (!stack.isEmpty()) {root = stack.poll();lower = lowers.poll();upper = uppers.poll();if (root == null) continue;val = root.val;if (lower != null && val <= lower) return false;if (upper != null && val >= upper) return false;update(root.right, val, upper);update(root.left, lower, val);}return true;}}
中序遍历
左子树 -> 结点 -> 右子树的顺序。
上面的结点按照访问的顺序标号,你可以按照 1-2-3-4-5 的顺序来比较不同的策略。
左子树 -> 结点 -> 右子树 意味着对于二叉搜索树而言,每个元素都应该比下一个元素小。
因此,具有 {O}(N)O(N) 时间复杂度与 {O}(N)O(N) 空间复杂度的算法十分简单:
计算中序遍历列表 inorder.
检查 inorder中的每个元素是否小于下一个。
我们需要保留整个inorder列表吗?事实上不需要。每一步最后一个添加的元素就足以保证树是(或不是)二叉搜索树。因此,我们可以将步骤整合并复用空间。
class Solution {public boolean isValidBST(TreeNode root) {Stack<TreeNode> stack = new Stack();double inorder = - Double.MAX_VALUE;while (!stack.isEmpty() || root != null) {while (root != null) {stack.push(root);root = root.left;}root = stack.pop();// If next element in inorder traversal// is smaller than the previous one// that's not BST.if (root.val <= inorder) return false;inorder = root.val;root = root.right;}return true;}}
复杂度分析
时间复杂度 : 最坏情况下(树为二叉搜索树或破坏条件的元素是最右叶结点)为 {O}(N)O(N)。
空间复杂度 : {O}(N)O(N) 用于存储 stack。
存储方式
链式存储结构
二叉树的链式存储结构中,每一个结点包含三个关键属性:指向左子树的指针,数据域,指向右子树的指针;根据这个叙述,我们可以按如下结构定义结点。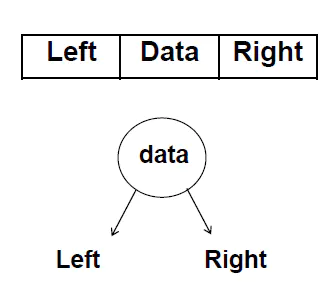
结点定义
public class BinaryTree <T>{private BinaryTree<T> leftChild;private BinaryTree<T> rightChild;private T data;public BinaryTree() {}public BinaryTree(T data) {this(data, null, null);}public BinaryTree(T data, BinaryTree<T> leftChild, BinaryTree<T> rightChild) {this.leftChild = leftChild;this.rightChild = rightChild;this.data = data;}public T getData() {return data;}public BinaryTree<T> getLeftChild() {return leftChild;}public BinaryTree<T> getRightChild() {return rightChild;}}
顺序存储结构
基于数组的顺序存储
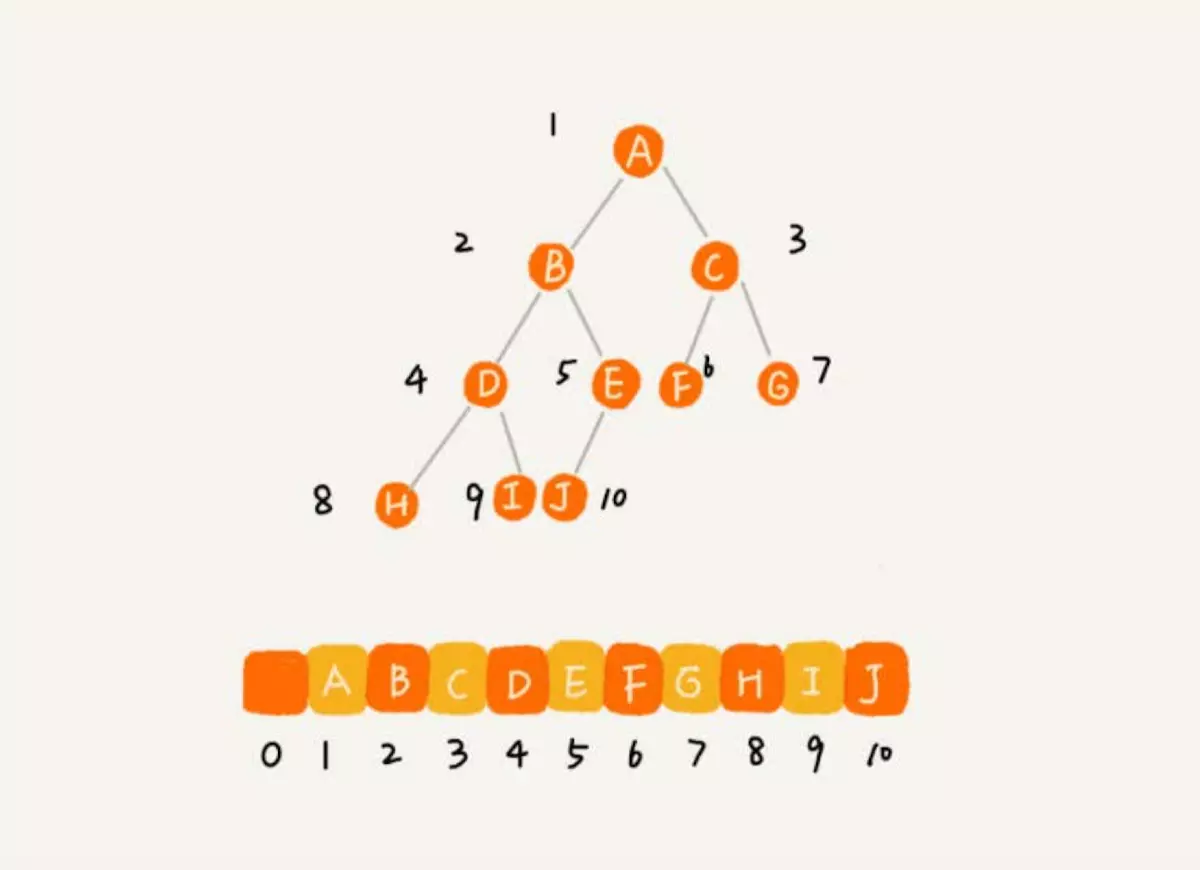
按照层级顺序把二叉树的节点放到数组对应的位置上,如果某一个节点的左孩子或右孩子空缺,则数组对应的位置也空出来。
父节点的下标是parent,那么它的左孩子节点下标是2_parent+1;右孩子节点下标是就是2_parnet+2
反过来假设一个左孩子节点是lefChild,那么它的父节点下标就是(leftChild-1)/2
二叉树的最大深度
通过递归方式实现数的最大深度
class Solution {public int maxDepth(TreeNode root) {if (root == null) {return 0;} else {int left_height = maxDepth(root.left);int right_height = maxDepth(root.right);return java.lang.Math.max(left_height, right_height) + 1;}}}
我们的想法是使用 DFS 策略访问每个结点,同时在每次访问时更新最大深度。
所以我们从包含根结点且相应深度为 1 的栈开始。然后我们继续迭代:将当前结点弹出栈并推入子结点。每一步都会更新深度。
import javafx.util.Pair;import java.lang.Math;class Solution {public int maxDepth(TreeNode root) {Queue<Pair<TreeNode, Integer>> stack = new LinkedList<>();if (root != null) {stack.add(new Pair(root, 1));}int depth = 0;while (!stack.isEmpty()) {Pair<TreeNode, Integer> current = stack.poll();root = current.getKey();int current_depth = current.getValue();if (root != null) {depth = Math.max(depth, current_depth);stack.add(new Pair(root.left, current_depth + 1));stack.add(new Pair(root.right, current_depth + 1));}}return depth;}};
复杂度分析
时间复杂度:O(N)O(N)。
空间复杂度:O(N)O(N)。
二叉树遍历
遍历是一种线性操作,数组和链表都是线性结构,对其进行遍历是非常容易的事情,而二叉树是典型的非线性数据结构,因此遍历时需要把非线性关联的节点转成一个线性的序列。
前序遍历:对于树中的任意节点来说,先打印这个节点,然后再打印它的左子树,最后打印它的右子树。中序遍历:对于树中的任意节点来说,先打印它的左子树,然后再打印它本身,最后打印它的右子树。后序遍历:对于树中的任意节点来说,先打印它的左子树,然后再打印它的右子树,最后打印这个节点本身。
BinaryTree<String> nodeH = new BinaryTree<>("H");BinaryTree<String> nodeG = new BinaryTree<>("G");BinaryTree<String> nodeF = new BinaryTree<>(nodeH, "F", null);BinaryTree<String> nodeE = new BinaryTree<>(nodeG, "E", null);BinaryTree<String> nodeD = new BinaryTree<>("D");BinaryTree<String> nodeC = new BinaryTree<>(null, "C", nodeF);BinaryTree<String> nodeB = new BinaryTree<>(nodeD, "B", nodeE);BinaryTree<String> root = new BinaryTree<>(nodeB, "A", nodeC);
前序遍历
输出顺序是根节点,左子树,右子树。即根节点—>左子树—>右子树
public static void preTraversal(BinaryTree node) {if (node != null) {System.out.print(node.getData().toString());preTraversal(node.getLeftChild());preTraversal(node.getRightChild());}}
非递归
public static void preTraversalIteration(BinaryTree node) {// 创建一个栈Stack<BinaryTree> mStack = new Stack<>();while (true) {while (node != null) { // 非叶子结点的子树// 前序遍历,先访问根结点System.out.print(node.getData().toString());// 将当前结点压入栈mStack.push(node);// 对左子树继续进行前序遍历node=node.getLeftChild();}if (mStack.isEmpty()) {//所有元素已遍历完成break;}// 弹出栈顶结点node=mStack.pop();// 右子树前序遍历node=node.getRightChild();}}
中序遍历
输出顺序是左子树,根节点,右子树,即左子树—>根节点—>右子树
步骤:首先访问根节点的左孩子,如果左孩子还拥有左孩子,则继续深入访问下去,一直找不到左孩子的节点,并输出该节点
递归方法实现
public static void preTraversal(BinaryTree node) {if (node != null) {preTraversal(node.getLeftChild());System.out.print(node.getData().toString());preTraversal(node.getRightChild());}}
堆栈实现
/*** 中序遍历-迭代实现* @param node*/public static void TraversalIteration(BinaryTree node) {// 创建一个栈Stack<BinaryTree> mStack = new Stack<>();while (true) {while (node != null) { // 非叶子结点的子树// 将当前结点压入栈mStack.push(node);// 对左子树继续进行中序遍历node=node.getLeftChild();}if (mStack.isEmpty()) {//所有元素已遍历完成break;}// 弹出栈顶结点node=mStack.pop();// 中序遍历,访问根结点System.out.print(node.getData().toString());// 右子树中序遍历node=node.getRightChild();}}
后序遍历
输出顺序是左子树,右子树,根节点,即左子树—>右子树—>根节点
public static void postTraversal(BinaryTree node) {if (node != null) {preTraversal(node.getLeftChild());preTraversal(node.getRightChild());System.out.print(node.getData().toString());}}
/*** 后序遍历-迭代实现* @param node*/public static void postTraversalIteration(BinaryTree node) {// 创建一个栈Stack<BinaryTree> mStack = new Stack<>();while (true) {if (node != null) {//当前结点非空,压入栈mStack.push(node);// 左子树继续遍历node=node.getLeftChild();}else {// 左子树为空if(mStack.isEmpty()){return;}if (mStack.lastElement().getRightChild() == null) {// 栈顶元素右子树为空,则当前结点为叶子结点,输出node=mStack.pop();System.out.print(node.getData().toString());while (node == mStack.lastElement().getRightChild()) {System.out.print(mStack.lastElement().getData().toString());node=mStack.pop();if (mStack.isEmpty()) {break;}}}if (!mStack.isEmpty()) {node=mStack.lastElement().getRightChild();}else {node=null;}}}}
层次遍历
层序遍历就是从上到下按层,从左至右依次访问每个结点。这种遍历非常用规律,就是从根节点下一层开始,优先访问每一层所有的双亲结点,然后依次访问每个结点的左右儿子。也就是说,从上到下,先遇见到结点先访问,后遇到的结点后访问,这典型的就是队列的思想
public static void levelTraversal(BinaryTree node) {//创建队列Queue<BinaryTree> mNodeQueue = new LinkedList<>();// 根结点加入队列mNodeQueue.add(node);BinaryTree temp;while (!mNodeQueue.isEmpty()) {//元素出队列temp=mNodeQueue.poll();//输出System.out.print(temp.getData().toString());if (temp.getLeftChild() != null) {// 左子树入队列mNodeQueue.add(temp.getLeftChild());}if (temp.getRightChild() != null) {//右子树入队列mNodeQueue.add(temp.getRightChild());}}}
遍历方法总结
递归
递归方法最为直观易懂,但考虑到效率,我们通常不推荐使用递归。
class Solution {public List < Integer > inorderTraversal(TreeNode root) {List < Integer > res = new ArrayList < > ();helper(root, res);return res;}public void helper(TreeNode root, List < Integer > res) {if (root != null) {if (root.left != null) {helper(root.left, res);}res.add(root.val);if (root.right != null) {helper(root.right, res);}}}}
时间复杂度:O(n)O(n)。递归函数 T(n) = 2 \cdot T(n/2)+1T(n)=2⋅T(n/2)+1。
空间复杂度:最坏情况下需要空间O(n)O(n),平均情况为O(\log n)O(logn)。
栈
利用栈,去模拟递归。递归压栈的过程,就是保存现场,就是保存当前的变量,而解法一中当前有用的变量就是 node,所以我们用栈把每次的 node 保存起来即可。
模拟下递归的过程,只考虑 node 的压栈。
//当前节点为空,出栈if (node == null) {return;}//当前节点不为空getAns(node.left, ans); //压栈ans.add(node.val); //出栈后添加getAns(node.right, ans); //压栈//左右子树遍历完,出栈
1/ \2 3/ \ /4 5 6push push push pop pop push pop pop| | | | |_4_| | | | | | | | | | || | |_2_| |_2_| |_2_| | | |_5_| | | | ||_1_| |_1_| |_1_| |_1_| |_1_| |_1_| |_1_| | |ans add 4 add 2 add 5 add 1[] [4] [4 2] [4 2 5] [4 2 5 1]push push pop pop| | | | | | | || | |_6_| | | | ||_3_| |_3_| |_3_| | |add 6 add 3[4 2 5 1 6] [4 2 5 1 6 3]
public class Solution {
public List < Integer > inorderTraversal(TreeNode root) {
List < Integer > res = new ArrayList < > ();
Stack < TreeNode > stack = new Stack < > ();
TreeNode curr = root;
while (curr != null || !stack.isEmpty()) {
while (curr != null) {
stack.push(curr);
curr = curr.left;
}
curr = stack.pop();
res.add(curr.val);
curr = curr.right;
}
return res;
}
}
复杂度分析
时间复杂度:O(n)O(n)。
空间复杂度:O(n)O(n)。
莫里斯遍历
使用一种新的数据结构:线索二叉树。方法如下:
Step 1: 将当前节点current初始化为根节点
Step 2: While current不为空,
若current没有左子节点
a. 将current添加到输出
b. 进入右子树,亦即, current = current.right
否则
a. 在current的左子树中,令current成为最右侧节点的右子节点
b. 进入左子树,亦即,current = current.left
举例而言:
1<br /> / \<br /> 2 3<br /> / \ /<br /> 4 5 6
首先,1 是根节点,所以将 current 初始化为 1。1 有左子节点 2,current 的左子树是
2<br /> / \<br /> 4 5<br />在此左子树中最右侧的节点是 5,于是将 current(1) 作为 5 的右子节点。令 current = cuurent.left (current = 2)。<br />现在二叉树的形状为:
2<br /> / \<br /> 4 5<br /> \<br /> 1<br /> \<br /> 3<br /> /<br /> 6<br />对于 current(2),其左子节点为4,我们可以继续上述过程
4<br /> \<br /> 2<br /> \<br /> 5<br /> \<br /> 1<br /> \<br /> 3<br /> /<br /> 6<br />由于 4 没有左子节点,添加 4 为输出,接着依次添加 2, 5, 1, 3 。节点 3 有左子节点 6,故重复以上过程。<br />最终的结果是 [4,2,5,1,6,3]。
class Solution {
public List < Integer > inorderTraversal(TreeNode root) {
List < Integer > res = new ArrayList < > ();
TreeNode curr = root;
TreeNode pre;
while (curr != null) {
if (curr.left == null) {
res.add(curr.val);
curr = curr.right; // move to next right node
} else { // has a left subtree
pre = curr.left;
while (pre.right != null) { // find rightmost
pre = pre.right;
}
pre.right = curr; // put cur after the pre node
TreeNode temp = curr; // store cur node
curr = curr.left; // move cur to the top of the new tree
temp.left = null; // original cur left be null, avoid infinite loops
}
}
return res;
}
}
复杂度分析
时间复杂度:O(n)O(n)。 想要证明时间复杂度是O(n)O(n),最大的问题是找到每个节点的前驱节点的时间复杂度。乍一想,找到每个节点的前驱节点的时间复杂度应该是 O(n\log n)O(nlogn),因为找到一个节点的前驱节点和树的高度有关。
但事实上,找到所有节点的前驱节点只需要O(n)O(n) 时间。一棵 nn 个节点的二叉树只有 n-1n−1 条边,每条边只可能使用2次,一次是定位节点,一次是找前驱节点。
故复杂度为 O(n)O(n)。
空间复杂度:O(n)O(n)。使用了长度为 nn 的数组。
// 莫里斯遍历利用叶子节点左右空域存储遍历前驱和后继
// 达到时间复杂度O(N),空间复杂度O(1)
// 二叉树的串行遍历
// 莫里斯中序遍历
func MorrisTraverMid(root *TreeNode) []int {
if root == nil {
return nil
}
var result []int
// 游标节点初始化为根节点
cur := root
// 定义前驱节点
var pre *TreeNode
// 当没有遍历到最后情况
for cur != nil {
// 当游标节点没有左孩子
if cur.Left == nil {
// 加游标节点值加入结果集(visit)
result = append(result, cur.Val)
// 因为没有左孩子,进入右孩子
cur = cur.Right
continue
}
// 当游标有左孩子
// 1.找到左子树最右节点作为游标节点前驱
// 得到左子树
pre = cur.Left
// 找到左子树最右叶子节点
for pre.Right != nil && pre.Right != cur {
pre = pre.Right
}
// 最右叶子节点
if pre.Right == nil {
// 最右叶子节点与cur连接
pre.Right = cur
// 进入左子树
cur = cur.Left
continue
}
// 最右节点与cur相等(成环情况)
// visit cur
result = append(result, cur.Val)
// 破环
pre.Right = nil
// 进入右子树
cur = cur.Right
}
return result
}
标记法
使用颜色标记节点的状态,新节点为白色,已访问的节点为灰色。
如果遇到的节点为白色,则将其标记为灰色,然后将其右子节点、自身、左子节点依次入栈。
如果遇到的节点为灰色,则将节点的值输出。
class Solution {
class ColorNode {
TreeNode node;
String color;
public ColorNode(TreeNode node,String color){
this.node = node;
this.color = color;
}
}
public List<Integer> inorderTraversal(TreeNode root) {
if(root == null) return new ArrayList<Integer>();
List<Integer> res = new ArrayList<>();
Stack<ColorNode> stack = new Stack<>();
stack.push(new ColorNode(root,"white"));
while(!stack.empty()){
ColorNode cn = stack.pop();
if(cn.color.equals("white")){
if(cn.node.right != null) stack.push(new ColorNode(cn.node.right,"white"));
stack.push(new ColorNode(cn.node,"gray"));
if(cn.node.left != null)stack.push(new ColorNode(cn.node.left,"white"));
}else{
res.add(cn.node.val);
}
}
return res;
}
}

