概述

编程的角度来看，程序调用自身的编程技巧称为递归（recursion），递归的本质就是循环，就是一个函数直接或间接调用自身的一种方法，是通过函数来进行的循环。它通常把一个大型复杂的问题层层转化为一个与原问题相似的规模较小的问题来求解。
image.png

关注点

递归是一个反复调用自身的过程，它每一级的功能都是一样的，因此我们只需要关注一级递归的解决过程即可

  1. 整个递归的终止条件。递归应该在什么时候结束？
  2. 本级递归应该做什么：在这一级递归中，应该完成什么任务？
  3. 应该返回给上一级的返回值是什么？

递归要素

为了确保递归函数不会导致无限循环，它应具有以下属性：

  1. 一个简单的基本案例（basic case）（或一些案例） —— 不需要进一步的递归调用就可以直接计算答案的情况。 有时，基本案例也被称为 bottom cases，因为它们往往是问题被减少到最小规模的情况，也就是如果我们认为将问题划分为子问题是一种自上而下的方式的最下层。
  2. 一组规则，也称作递推关系（recurrence relation），一个问题的结果与其子问题的结果之间的关系。

寻找递归结束条件
函数的等价关系式

  1. int func(传入数值) {
  2.   if (终止条件) 
  3.     return 最小子问题解;
  4.   return func(缩小规模);
  5. }

递归模板

  1.     def recursion(level, p1, p2, ...):
  3.         # 递归终止条件
  4.         if level > MAX_LEVEL:
  5.             print(result)
  6.             return 
  8.         # 处理当前问题层逻辑
  9.         p1_pro, p2_pro = process_data(level, data...)
  11.         # 迭代下一层
  12.         self.recursion(level + 1, p1_pro, p2_pro, ...)
  14.         # 清理当前层
  15.         reverse_state(level)
  1. public void recur(int level, int param) { 
  3.   // 递归终止条件
  4.   if (level > MAX_LEVEL) { 
  5.     // process result 
  6.     return; 
  7.   } 
  9.   // 处理当前逻辑 
  10.   process(level, param); 
  12.   // 迭代下一层
  13.   recur( level: level + 1, newParam); 
  15.   // restore current status 
  17. }

迭代循环表示n 相加

  1.    public static int sum(int num){
  2.         int result =0;
  3.         for (int i =1;i<=num;i++){
  4.             result +=i;
  5.         }
  6.         return result;
  7.     }

n相加递归表达
当num是1 和是1，
对于n的和等于当前n加上n-1之前的和num+plusSum(num-1);

  1.     public static int plusSum(int num){
  2.        if (num==1)
  3.         return 1;
  4.        return num+plusSum(num-1);
  5.     }

同理 n的阶乘 表示也是一样的道理

  1.     public static int factorial(int n) {
  2.         if (n == 1)
  3.             return 1;
  4.         return n * factorial(n - 1);
  5.     }

递归与栈

递归的过程就是出入栈的过程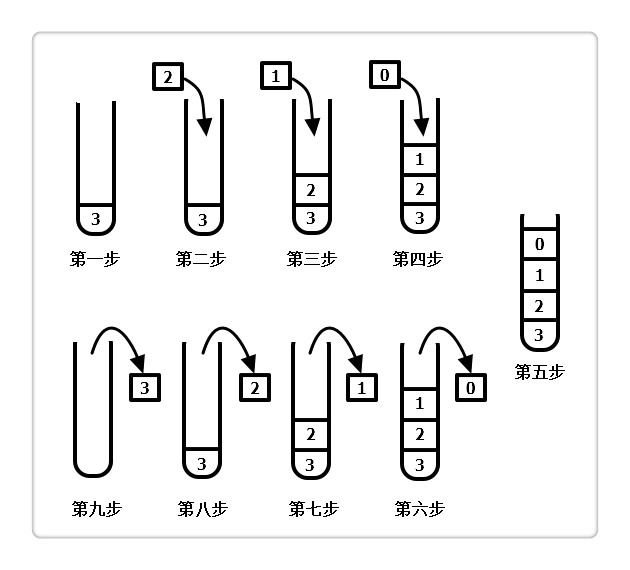
图片.png
第 1~4 步，都是入栈过程，Factorial(3)调用了Factorial(2)，Factorial(2)又接着调用Factorial(1)，直到Factorial(0)；
第 5 步，因 0 是递归结束条件，故不再入栈，此时栈高度为 4，即为我们平时所说的递归深度；
第 6~9 步，Factorial(0)做完，出栈，而Factorial(0)做完意味着Factorial(1)也做完，同样进行出栈，重复下去，直到所有的都出栈完毕，递归结束。
每一个递归程序都可以把它改写为非递归版本。我们只需利用栈，通过入栈和出栈两个操作就可以模拟递归的过程，二叉树的遍历无疑是这方面的代表。
但是并不是每个递归程序都是那么容易被改写为非递归的。某些递归程序比较复杂，其入栈和出栈非常繁琐，给编码带来了很大难度，而且易读性极差，所以条件允许的情况下，推荐使用递归。

精典问题

斐波那契数列

斐波那契数列的是这样一个数列：1、1、2、3、5、8、13、21、34….，即第一项 f(1) = 1,第二项 f(2) = 1…..,第 n 项目为 f(n) = f(n-1) + f(n-2)。求第 n 项的值是多少。

  1.     public static int fipolach(int n){
  2.         // 递归结束条件
  3.         if(n <= 2){
  4.             return 1;
  5.         }
  6.         // 2.等价关系式
  7.         return fipolach(n-1) + fipolach(n - 2);

小青蛙跳台阶

一只青蛙一次可以跳上1级台阶，也可以跳上2级。求该青蛙跳上一个n级的台阶总共有多少种跳法。

  1.     public static int stepNum(int n){
  2.         if(n <= 2){
  3.             return n;
  4.         }
  5.         return stepNum(n-1) + stepNum(n-2);
  6.     }

反转单链表

反转单链表。例如链表为：1->2->3->4。反转后为 4->3->2->1

  1. //用递归的方法反转链表
  2. public static Node reverseList2(Node head){
  3.     // 1.递归结束条件
  4.     if (head == null || head.next == null) {
  5.              return head;
  6.          }
  7.          // 递归反转 子链表
  8.          Node newList = reverseList2(head.next);
  9.          // 改变 1，2节点的指向。
  10.          // 通过 head.next获取节点2
  11.          Node t1  = head.next;
  12.          // 让 2 的 next 指向 2
  13.          t1.next = head;
  14.          // 1 的 next 指向 null.
  15.         head.next = null;
  16.         // 把调整之后的链表返回。
  17.         return newList;
  18.     }

汉诺塔

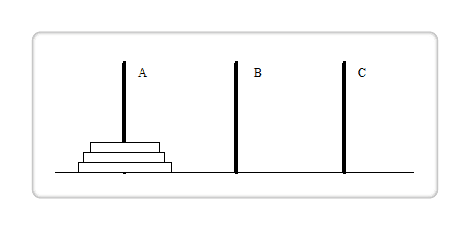
图片.png
问题描述为：有三根杆子 A，B，C。A 杆上有 N 个穿孔圆盘，盘的尺寸由上到下依次变大，B，C 杆为空。要求按下列规则将所有圆盘移至 C 杆：

  1. 每次只能移动一个圆盘；
  2. 大盘不能叠在小盘上面。
    问：如何移？最少要移动多少次？
    首先看下基本情况，即终止条件：N=1 时，直接从 A 移到 C。
    再来看下通用情况：当有 N 个圆盘在 A 上，我们已经找到办法将其移到 C 杠上了，我们怎么移动 N+1 个圆盘到 C 杠上呢？很简单，我们首先用将 N 个圆盘移动到 C 上的方法将 N 个圆盘都移动到 B 上，然后再把第 N+1 个圆盘（最后一个）移动到 C 上，再用同样的方法将在 B 杠上的 N 个圆盘移动到 C 上，问题解决。
  1. void Hanoi(int n, char a, char b, char c){    //终止条件
  2.    if (n == 1)
  3.     {
  4.          cout << a << "-->" << c << endl;        
  6.          return;
  8.     }    //通用情况
  10.     Hanoi(n - 1, a, c, b);
  12.     Hanoi(1, a, b, c);
  14.     Hanoi(n - 1, b, a, c);
  15.  }

二叉树的最大深度

  1. 找终止条件。 什么情况下递归结束？当然是树为空的时候，此时树的深度为0，递归就结束了。
  2. 找返回值。 应该返回什么？题目求的是树的最大深度，我们需要从每一级得到的信息自然是当前这一级对应的树的最大深度，因此我们的返回值应该是当前树的最大深度，这一步可以结合第三步来看。
  3. 本级递归应该做什么。 首先，还是强调要走出之前的思维误区，递归后我们眼里的树一定是这个样子的，看下图。此时就三个节点：root、root.left、root.right，其中根据第二步，root.left和root.right分别记录的是root的左右子树的最大深度。那么本级递归应该做什么就很明确了，自然就是在root的左右子树中选择较大的一个，再加上1就是以root为根的子树的最大深度了，然后再返回这个深度即可。

image.png
图片来源于https://lyl0724.github.io/2020/01/25/1/

  1. class Solution {
  2.     public int maxDepth(TreeNode root) {
  3.         //终止条件：当树为空时结束递归，并返回当前深度0
  4.         if(root == null){
  5.             return 0;
  6.         }
  7.         //root的左、右子树的最大深度
  8.         int leftDepth = maxDepth(root.left);
  9.         int rightDepth = maxDepth(root.right);
  10.         //返回的是左右子树的最大深度+1
  11.         return Math.max(leftDepth, rightDepth) + 1;
  12.     }
  13. }

或者

  1. class Solution {
  2.     public int maxDepth(TreeNode root) {
  3.         return root == null ? 0 : Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
  4.     }
  5. }

两两交换链表中的节点

  1. 找终止条件。 什么情况下递归终止？没得交换的时候，递归就终止了呗。因此当链表只剩一个节点或者没有节点的时候，自然递归就终止了。
  2. 找返回值。 我们希望向上一级递归返回什么信息？由于我们的目的是两两交换链表中相邻的节点，因此自然希望交换给上一级递归的是已经完成交换处理，即已经处理好的链表。
  3. 本级递归应该做什么。 结合第二步，看下图！由于只考虑本级递归，所以这个链表在我们眼里其实也就三个节点：head、head.next、已处理完的链表部分。而本级递归的任务也就是交换这3个节点中的前两个节点，就很easy了。
  1. class Solution {
  2.     public ListNode swapPairs(ListNode head) {
  3.           //终止条件：链表只剩一个节点或者没节点了，没得交换了。返回的是已经处理好的链表
  4.         if(head == null || head.next == null){
  5.             return head;
  6.         }
  7.           //一共三个节点:head, next, swapPairs(next.next)
  8.           //下面的任务便是交换这3个节点中的前两个节点
  9.         ListNode next = head.next;
  10.         head.next = swapPairs(next.next);
  11.         next.next = head;
  12.           //根据第二步：返回给上一级的是当前已经完成交换后，即处理好了的链表部分
  13.         return next;
  14.     }
  15. }

参考

https://mp.weixin.qq.com/s/mJ_jZZoak7uhItNgnfmZvQ
https://lyl0724.github.io/2020/01/25/1/