数据结构 - 跳表/SkipList - 《Leetcode》

节点
查找
复杂度
1206. 设计跳表">1206. 设计跳表
ConcurrentSkipListMap
参考

跳跃表是一种特殊的有序链表。通过空间换时间的方式解决链表查询效率低下的问题。
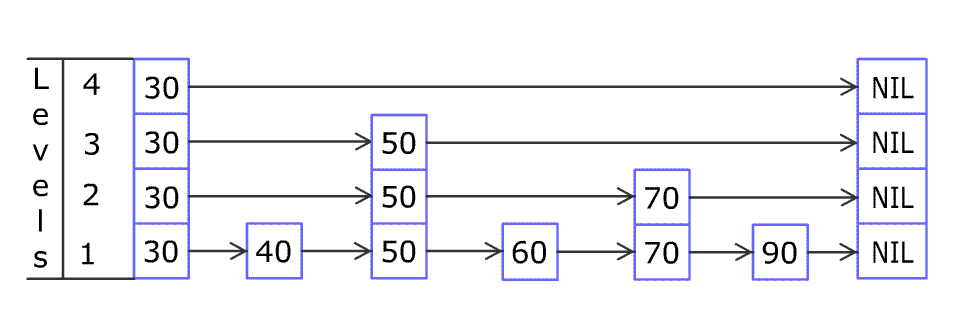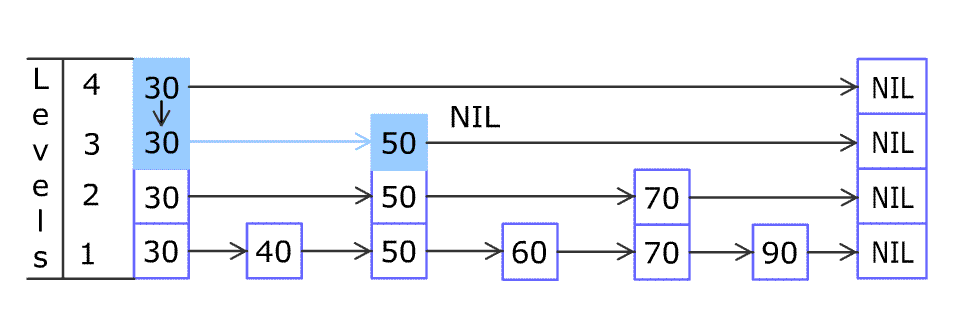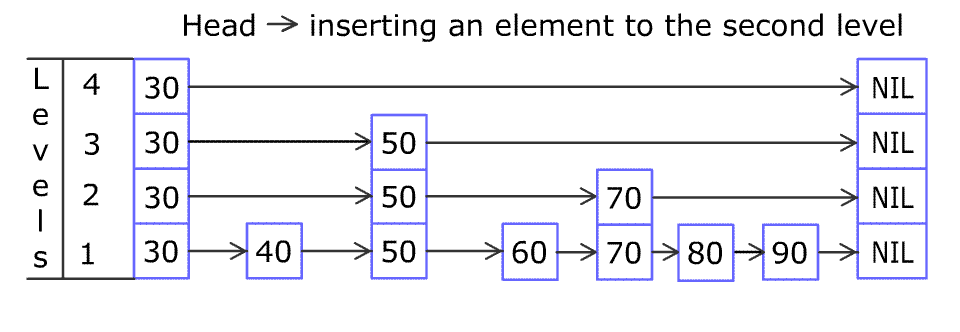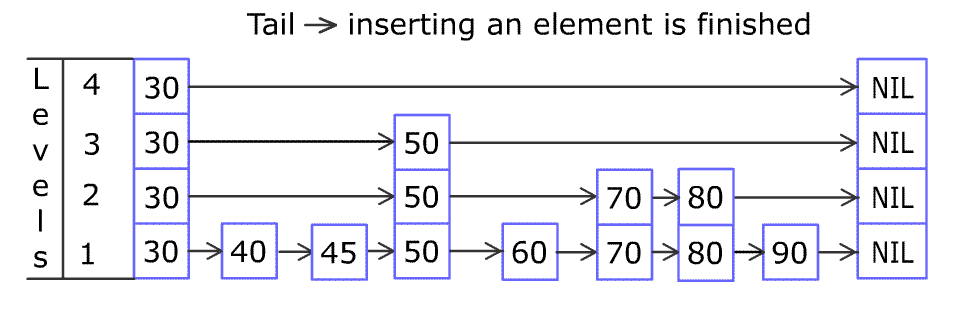
跳跃表是由多层有序链表组合而成的，最底一层的保存所有的数据，每向上的一层链表以此保存了下一层链表的部分数据,相邻的两层链表中元素相同的节点之间存在引用关系，一般上层的节点存在一个指向下层节点的引用。总的来说跳表=链表+多级索引。

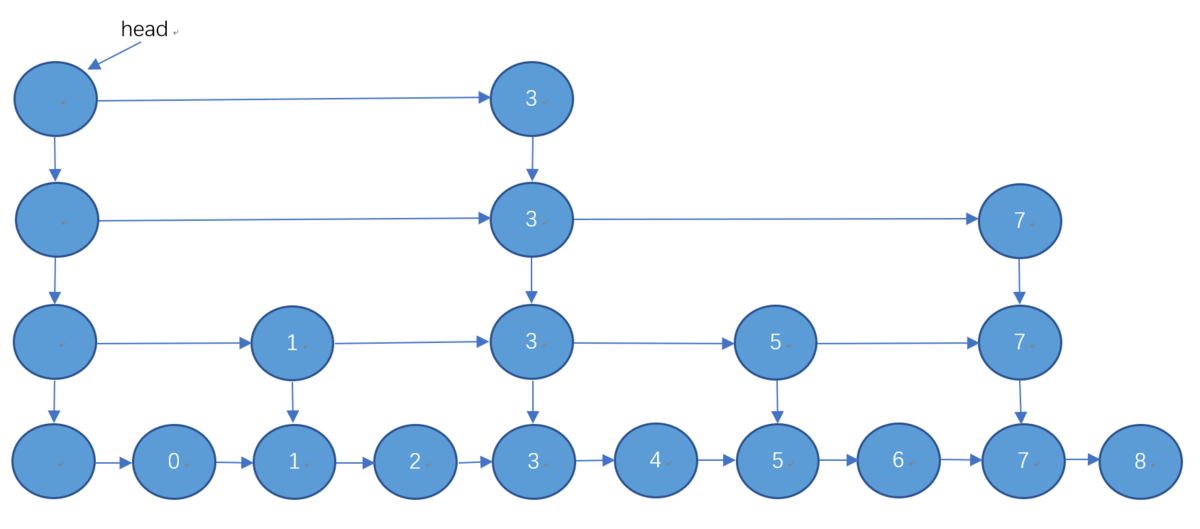
图片.png

节点

查找

查找操作是自顶向下，从左到右，即从最上一层链表中从左到右查找，然后以此向下层查找，指导最下一层的某个节点结束
1 先从最上一层查找小于所指定元素的最右的节点，将节点入栈，然后转向下一层。
2 在当前层继续查找满足上述条件的节点，同样将其入栈，向下一层继续查找，直到找到最下一层满足条件的节点。
在查找的时候，从最上层开始找，因为最顶层元素最少，比较次数也少，如果在较上层找到了，直接返回 true ；如果在较上层比较时发现了更大的元素，或者到头了，说明再往后是找不见的，直接向下层跳即可（所以这里需要记录访问的前一个元素是什么以进行向下的跳跃，可以多加一个元素在循环的时候记录前次访问的元素，或者使用双链表实现）。直到跳到最后一层还是没到，那就是找不到了，返回 false 。

复杂度

跳表的平均查找和插入时间复杂度都是O(log n)，优于普通队列的O(n)，。
空间复杂度O(n)，它因为建立了多级索引，因此非常耗内存（）。它的查找借鉴了二分查找。利用空间换时间，根据随机数建立多级索引。

完整代码

package com.github.linkedList;
import java.util.Random;
public class SkipList {
    /**
     * @Description 最高层数是16
     */
    private static final int MAX_LEVEL = 1 <<4;
    /**
     * @Description 链表最高层数
     */
    private int levelCount = 1;
    /**
     * 哨兵结点，哨兵结点的层数就是是跳表层数的最大值
     */
    private Node head = new Node(MAX_LEVEL);
    private Random r = new Random();
    public Node find(int value) {
        Node p = head;
        // 从最高层开始往下一直查找到最底下的原始数据层，
        for (int i = levelCount - 1; i >= 0; --i) {
            //横向遍历当前层，找到比查找数值小的前一节点，移动到下层再开始查找
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                // 找到前一节点
                p = p.forwards[i];
            }
        }
        // 0 就是我们存储原始数据层，如果原始数据层的前一个节点的下一个值等于查找值就返回
        if (p.forwards[0] != null && p.forwards[0].data == value) {
            return p.forwards[0];
        } else {
            return null;
        }
    }
    /**
     * 优化了作者zheng的插入方法
     *
     * @param value 值
     */
    public void insert(int value) {
        int level = head.forwards[0] == null ? 1 : randomLevel();
        // 每次只增加一层，如果条件满足
        if (level > levelCount) {
            level = ++levelCount;
        }
        Node newNode = new Node(level);
        newNode.data = value;
        Node update[] = new Node[level];
        for (int i = 0; i < level; ++i) {
            update[i] = head;
        }
        Node p = head;
        // 从最大层开始查找，找到前一节点，通过--i，移动到下层再开始查找
        for (int i = levelCount - 1; i >= 0; --i) {
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                // 找到前一节点
                p = p.forwards[i];
            }
            // levelCount 会 > level，所以加上判断
            if (level > i) {
                update[i] = p;
            }
        }
        for (int i = 0; i < level; ++i) {
            newNode.forwards[i] = update[i].forwards[i];
            update[i].forwards[i] = newNode;
        }
    }
    /**
     * 优化了作者zheng的插入方法2
     *
     * @param value 值
     */
    public void insert2(int value) {
        int level = head.forwards[0] == null ? 1 : randomLevel();
        // 每次只增加一层，如果条件满足
        if (level > levelCount) {
            level = ++levelCount;
        }
        Node newNode = new Node(level);
        newNode.data = value;
        Node p = head;
        // 从最大层开始查找，找到前一节点，通过--i，移动到下层再开始查找
        for (int i = levelCount - 1; i >= 0; --i) {
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                // 找到前一节点
                p = p.forwards[i];
            }
            // levelCount 会 > level，所以加上判断
            if (level > i) {
                if (p.forwards[i] == null) {
                    p.forwards[i] = newNode;
                } else {
                    Node next = p.forwards[i];
                    p.forwards[i] = newNode;
                    newNode.forwards[i] = next;
                }
            }
        }
    }
    /**
     * 作者zheng的插入方法，未优化前，优化后参见上面insert()
     *
     * @param value
     * @param level 0 表示随机层数，不为0，表示指定层数，指定层数
     *              可以让每次打印结果不变动，这里是为了便于学习理解
     */
    public void insert(int value, int level) {
        // 随机一个层数
        if (level == 0) {
            //需要注意的是如果随机level=1，那么插入时间复杂度为O（n）
            level = randomLevel();
        }
        // 创建新节点
        Node newNode = new Node(level);
        newNode.data = value;
        // 记录要更新的层数，表示新节点要更新到哪几层
        Node update[] = new Node[level];
        for (int i = 0; i < level; ++i) {
            update[i] = head;
        }
        /**
         *
         * 查找前一个节点
         * 1，说明：层是从下到上的，这里最下数据层是0，目前设置的索引层依次是1-15
         * 2，这里没有从已有数据最大层（编号最大）开始找，（而是随机层的最大层）导致有些问题。
         */
        Node p = head;
        for (int i = level - 1; i >= 0; --i) {
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                p = p.forwards[i];
            }
            // 这里update[i]表示当前层节点的前一节点，因为要找到前一节点，才好插入数据
            update[i] = p;
        }
        // 将每一层节点和后面节点关联
        for (int i = 0; i < level; ++i) {
            // 记录当前层节点后面节点指针
            newNode.forwards[i] = update[i].forwards[i];
            // 前一个节点的指针，指向当前节点
            update[i].forwards[i] = newNode;
        }
        // 更新层高
        if (levelCount < level) levelCount = level;
    }
    public void delete(int value) {
        Node[] update = new Node[levelCount];
        Node p = head;
        for (int i = levelCount - 1; i >= 0; --i) {
            while (p.forwards[i] != null && p.forwards[i].data < value) {
                p = p.forwards[i];
            }
            update[i] = p;
        }
        if (p.forwards[0] != null && p.forwards[0].data == value) {
            for (int i = levelCount - 1; i >= 0; --i) {
                if (update[i].forwards[i] != null && update[i].forwards[i].data == value) {
                    update[i].forwards[i] = update[i].forwards[i].forwards[i];
                }
            }
        }
    }
    /**
     * 随机 level 次，如果是奇数层数 +1，防止伪随机
     *
     * @return
     */
    private int randomLevel() {
        int level = 1;
        for (int i = 1; i < MAX_LEVEL; ++i) {
            if (r.nextInt() % 2 == 1) {
                level++;
            }
        }
        return level;
    }
    /**
     * 打印每个节点数据和最大层数
     */
    public void printAll() {
        Node p = head;
        while (p.forwards[0] != null) {
            System.out.print(p.forwards[0] + " ");
            p = p.forwards[0];
        }
        System.out.println();
    }
    /**
     * 跳表的节点，每个节点存储了当前节点数据和所在层数数据
     */
    public class Node {
        /**
         * 当前节点的数值 默认值选择了-1
         */
        private int data = -1;
        /**
         * 表示当前节点位置的下一个节点所有层的数据，从上层切换到下层，就是数组下标-1，
         * forwards[3]表示当前节点在第三层的下一个节点。
         */
        private Node forwards[];
        public Node(int level) {
            forwards = new Node[level];
        }
        @Override
        public String toString() {
            StringBuilder builder = new StringBuilder();
            builder.append("{ data: ");
            builder.append(data);
            builder.append("; levels: ");
            builder.append(" }");
            return builder.toString();
        }
    }
    public static void main(String[] args) {
        SkipList list = new SkipList();
        list.insert(0, 1);
        list.insert(1, 2);
        list.insert(2, 1);
        list.insert(3, 4);
        list.insert(4, 1);
        list.insert(5, 2);
        list.insert(6, 1);
        list.insert(7, 1);
        list.insert(8, 3);
        Node node = list.find(7);
       for (int i=0;i<node.forwards.length;i++){
           System.out.println(i+":"+node.forwards[i].data);
       }
 //       list.insert(2, 3);
//        list.insert(3, 2);
//        list.insert(4, 4);
//        list.insert(5, 10);
//        list.insert(6, 4);
//        list.insert(8, 5);
//        list.insert(7, 4);
        list.printAll();
        /**
         * 结果如下：
         *                                         null:15-------
         *                                         null:14-------
         *                                         null:13-------
         *                                         null:12-------
         *                                         null:11-------
         *                                         null:10-------
         *                                            5:9-------
         *                                            5:8-------
         *                                            5:7-------
         *                                            5:6-------
         *                                            5:5-------
         *                                            5:4-------                     8:4-------
         *                                  4:3-------5:3-------6:3-------7:3-------8:3-------
         * 1:2-------2:2-------             4:2-------5:2-------6:2-------7:2-------8:2-------
         * 1:1-------2:1-------3:1-------4:1-------5:1-------6:1-------7:1-------8:1-------
         * 1:0-------2:0-------3:0-------4:0-------5:0-------6:0-------7:0-------8:0-------
         * { data: 1; levels: 3 } { data: 2; levels: 3 } { data: 3; levels: 2 } { data: 4; levels: 4 }
         * { data: 5; levels: 10 } { data: 6; levels: 4 } { data: 7; levels: 4 } { data: 8; levels: 5 }
         */
        // 优化后insert()
//        SkipList list2 = new SkipList();
//        list2.insert2(1);
//        list2.insert2(2);
//        list2.insert2(6);
//        list2.insert2(7);
//        list2.insert2(8);
//        list2.insert2(3);
//        list2.insert2(4);
//        list2.insert2(5);
//        System.out.println();
//        list2.printAll_beautiful();
    }
}

1206. 设计跳表

ConcurrentSkipListMap

参考

https://juejin.im/post/5c7bcc9e6fb9a049a5719f70
https://juejin.im/post/57fa935b0e3dd90057c50fbc
https://juejin.im/post/5cdc38236fb9a0322d04ac7b
https://juejin.im/post/5cf8c50ff265da1b76389223
https://www.01hai.com/note/av127380