爬楼梯

图片.png
上 1 阶台阶：有1种方式。
上 2 阶台阶：有1+1和2两种方式。
上 3 阶台阶：到达第3阶的方法总数就是到第1阶和第2阶的方法数之和。
上 n 阶台阶，到达第n阶的方法总数就是到第 (n-1) 阶和第 (n-2) 阶的方法数之和。

台阶数 1 2 3 4 5 6
方法总数 1 2 3 5 8 13

我们令 dp[n] 表示能到达第 n 阶的方法总数，可以得到如下状态转移方程：

dp[n]=dp[n-1]+dp[n-2]

  1. func climbStairs(n int) int {
  2.     if n==1 {
  3.         return 1
  4.     }
  5.     dp :=make([]int,n+1)
  6.     dp[1]=1
  7.     dp[2]=2
  8.     for i:=3;i<=n;i++{
  9.         dp[i]=dp[i-1]+dp[i-2]
  10.     }
  11.     return dp[n]
  12. }

最大子序和

图片.png
一个连续子数组一定要以一个数作为结尾,将状态定义成如下：
dp[i]：表示以 nums[i] 结尾的连续子数组的最大和。
状态转移方程其实是通过1-3个参数的方程来描述小规模问题和大规模问题间的关系。
如果要得到dp[i]，那么nums[i]一定会被选取。并且 dp[i] 所表示的连续子序列与 dp[i-1] 所表示的连续子序列很可能就差一个 nums[i] 。即
dp[i] = dp[i-1]+nums[i] , if (dp[i-1] >= 0)
很有可能dp[i-1]本身是一个负数。那这种情况的话，如果dp[i]通过dp[i-1]+nums[i]来推导，那么结果其实反而变小了，因为我们dp[i]要求的是最大和。所以在这种情况下，如果dp[i-1]<0，那么dp[i]其实就是nums[i]的值。即
dp[i] = nums[i] , if (dp[i-1] < 0)
综上分析，我们可以得到：
dp[i]=max(nums[i], dp[i−1]+nums[i])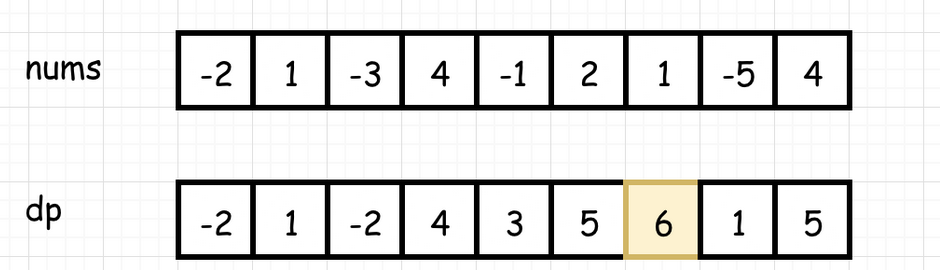


图片.png

  1. package main
  3. import "fmt"
  5. func maxSubArray(nums []int) int {
  6.     len :=len(nums)
  7.     // 定义动态数组
  8.     dp :=make([]int,len)
  9.     // 最大结果是第一个数
  10.     result := nums[0]
  11.     // 第一个值
  12.     dp[0]=nums[0]
  13.     for i:=1;i<len;i++{
  14.         dp[i] =Max(dp[i-1]+nums[i],nums[i])
  15.         result = Max(dp[i],result)
  16.     }
  17.     return result
  18. }
  20. func Max(a,b int)int{
  21.     if a>b {
  22.         return a
  23.     }
  24.     return b
  25. }
  27. //53. 最大子序和 https://leetcode-cn.com/problems/maximum-subarray/
  28. func main() {
  29.     //fmt.Println(maxSubArray([]int{-2}))
  30.     //fmt.Println(maxSubArray([]int{-2,1}))
  31.     fmt.Println(maxSubArray([]int{-2,1,-3}))
  32.     fmt.Println(maxSubArray([]int{2,1,-3,4,-1,2,1,-5,4}))
  33. }

**

斐波那契数列

步骤一、暴力的递归算法

  1. int fib(int N) {
  2.     if (N == 1 || N == 2) return 1;
  3.     return fib(N - 1) + fib(N - 2);
  4. }

这个不用多说了，学校老师讲递归的时候似乎都是拿这个举例。我们也知道这样写代码虽然简洁易懂，但是十分低效，低效在哪里？假设 n = 20，请画出递归树。
PS：但凡遇到需要递归的问题，最好都画出递归树，这对你分析算法的复杂度，寻找算法低效的原因都有巨大帮助。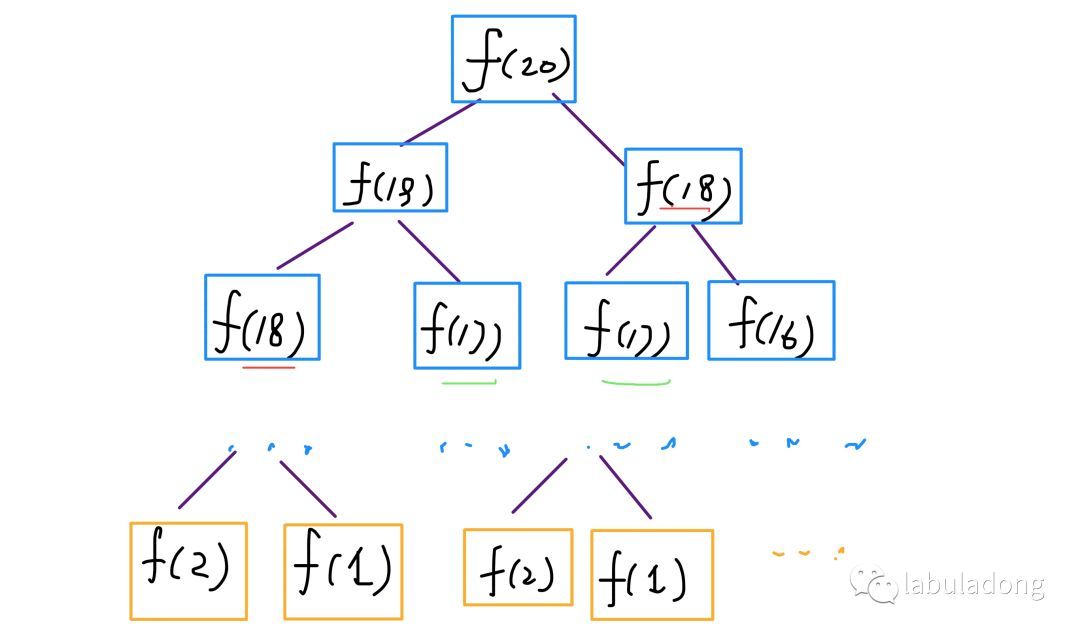
动态规划算法/DP - 图4
这个递归树怎么理解？就是说想要计算原问题 f(20)，我就得先计算出子问题 f(19) 和 f(18)，然后要计算 f(19)，我就要先算出子问题 f(18) 和 f(17)，以此类推。最后遇到 f(1) 或者 f(2) 的时候，结果已知，就能直接返回结果，递归树不再向下生长了。
递归算法的时间复杂度怎么计算？子问题个数乘以解决一个子问题需要的时间。
子问题个数，即递归树中节点的总数。显然二叉树节点总数为指数级别，所以子问题个数为 O(2^n)。
解决一个子问题的时间，在本算法中，没有循环，只有 f(n - 1) + f(n - 2) 一个加法操作，时间为 O(1)。
所以，这个算法的时间复杂度为 O(2^n)，指数级别，爆炸。
观察递归树，很明显发现了算法低效的原因：存在大量重复计算，比如 f(18) 被计算了两次，而且你可以看到，以 f(18) 为根的这个递归树体量巨大，多算一遍，会耗费巨大的时间。更何况，还不止 f(18) 这一个节点被重复计算，所以这个算法及其低效。
这就是动态规划问题的第一个性质：重叠子问题。下面，我们想办法解决这个问题。
步骤二、带备忘录的递归解法
明确了问题，其实就已经把问题解决了一半。即然耗时的原因是重复计算，那么我们可以造一个「备忘录」，每次算出某个子问题的答案后别急着返回，先记到「备忘录」里再返回；每次遇到一个子问题先去「备忘录」里查一查，如果发现之前已经解决过这个问题了，直接把答案拿出来用，不要再耗时去计算了。
一般使用一个数组充当这个「备忘录」，当然你也可以使用哈希表（字典），思想都是一样的。

  1. int fib(int N) {
  2.     if (N < 1) return 0;
  3.     // 备忘录全初始化为 0
  4.     vector<int> memo(N + 1, 0);
  5.     // 初始化最简情况
  6.     memo[1] = memo[2] = 1;
  7.     return helper(memo, N);
  8. }
  9. int helper(vector<int>& memo, int n) {
  10.     // 未被计算过
  11.     if (n > 0 && memo[n] == 0)
  12.         memo[n] = helper(memo, n - 1) + helper(memo, n - 2);
  13.     return memo[n];
  14. }

现在，画出递归树，你就知道「备忘录」到底做了什么。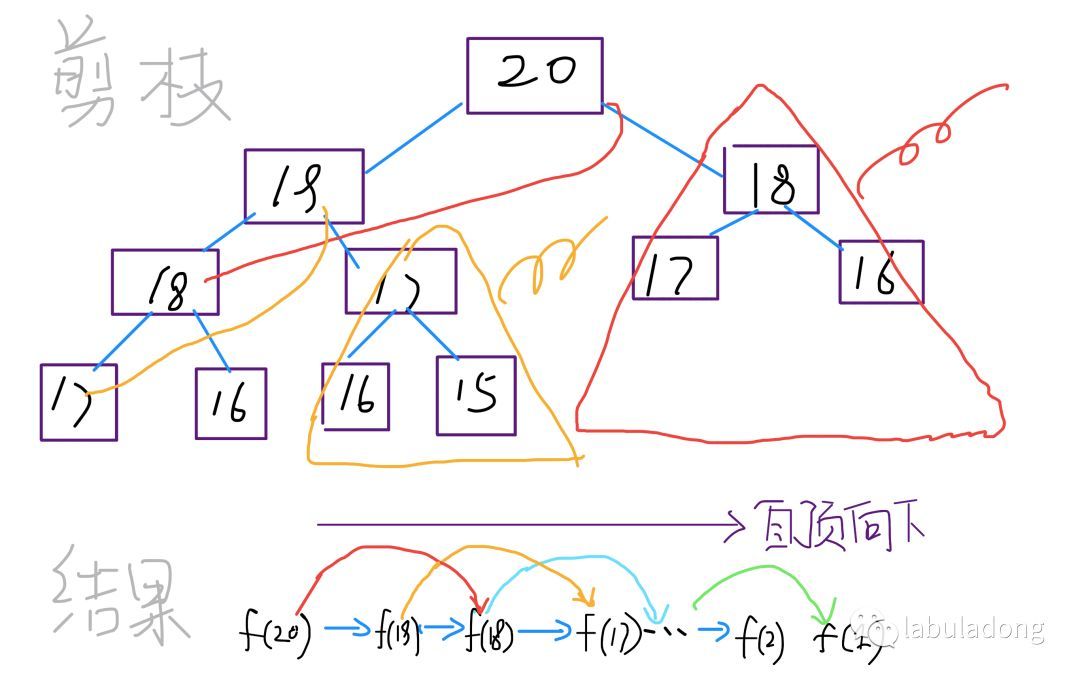
动态规划算法/DP - 图5
实际上，带「备忘录」的递归算法，把一棵存在巨量冗余的递归树通过「剪枝」，改造成了一幅不存在冗余的递归图，极大减少了子问题（即递归图中节点）的个数。
递归算法的时间复杂度怎么算？子问题个数乘以解决一个子问题需要的时间。
子问题个数，即图中节点的总数，由于本算法不存在冗余计算，子问题就是 f(1), f(2), f(3) … f(20)，数量和输入规模 n = 20 成正比，所以子问题个数为 O(n)。
解决一个子问题的时间，同上，没有什么循环，时间为 O(1)。
所以，本算法的时间复杂度是 O(n)。比起暴力算法，是降维打击。
至此，带备忘录的递归解法的效率已经和动态规划一样了。实际上，这种解法和动态规划的思想已经差不多了，只不过这种方法叫做「自顶向下」，动态规划叫做「自底向上」。
啥叫「自顶向下」？注意我们刚才画的递归树（或者说图），是从上向下延伸，都是从一个规模较大的原问题比如说 f(20)，向下逐渐分解规模，直到 f(1) 和 f(2) 触底，然后逐层返回答案，这就叫「自顶向下」。
啥叫「自底向上」？反过来，我们直接从最底下，最简单，问题规模最小的 f(1) 和 f(2) 开始往上推，直到推到我们想要的答案 f(20)，这就是动态规划的思路，这也是为什么动态规划一般都脱离了递归，而是由循环迭代完成计算。
步骤三、动态规划
有了上一步「备忘录」的启发，我们可以把这个「备忘录」独立出来成为一张表，就叫做 DP table 吧，在这张表上完成「自底向上」的推算岂不美哉！
int fib(int N) {
vector dp(N + 1, 0);
dp[1] = dp[2] = 1;
for (int i = 3; i <= N; i++)
dp[i] = dp[i - 1] + dp[i - 2];
return dp[N];
}
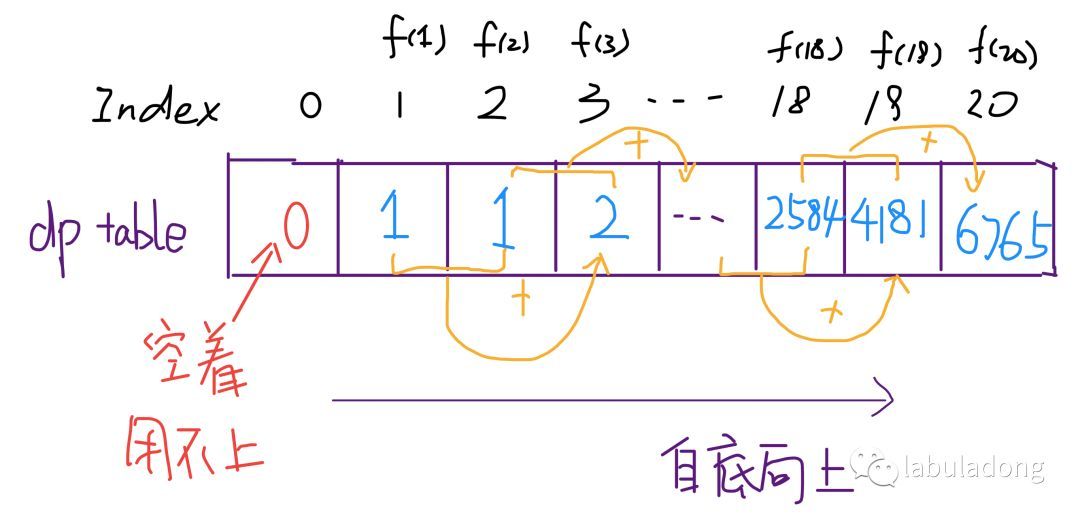
动态规划算法/DP - 图6
画个图就很好理解了，而且你发现这个 DP table 特别像之前那个「剪枝」后的结果，只是反过来算而已。实际上，带备忘录的递归解法中的「备忘录」，最终完成后就是这个 DP table，所以说这两种解法其实是差不多的，大部分情况下，效率也基本相同。
这里，引出「动态转移方程」这个名词，实际上就是描述问题结构的数学形式：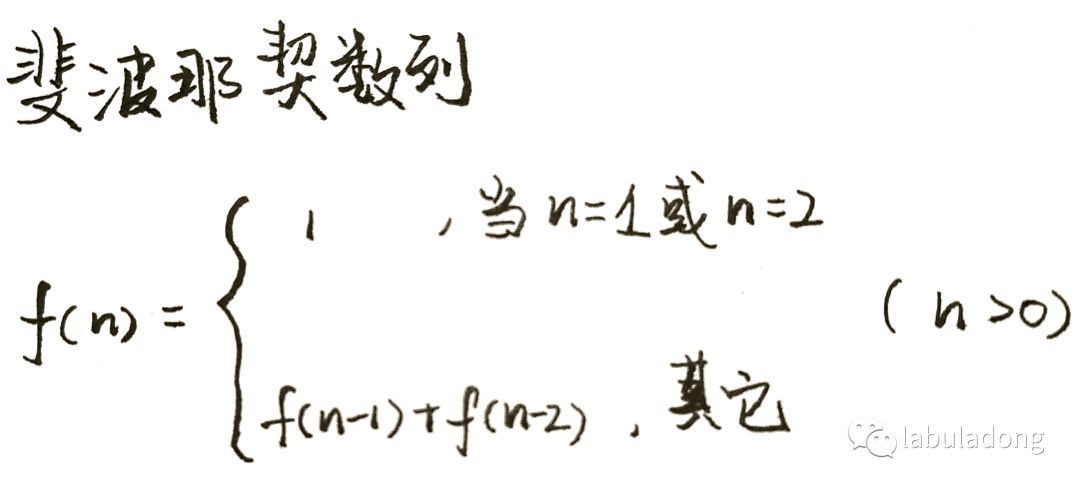
动态规划算法/DP - 图7
为啥叫「状态转移方程」？为了听起来高端。你把 f(n) 想做一个状态 n，这个状态 n 是由状态 n - 1 和状态 n - 2 相加转移而来，这就叫状态转移，仅此而已。
你会发现，上面的几种解法中的所有操作，例如 return f(n - 1) + f(n - 2)，dp[i] = dp[i - 1] + dp[i - 2]，以及对备忘录或 DP table 的初始化操作，都是围绕这个方程式的不同表现形式。可见列出「状态转移方程」的重要性，它是解决问题的核心。很容易发现，其实状态转移方程直接代表着暴力解法。
千万不要看不起暴力解，动态规划问题最困难的就是写出状态转移方程，即这个暴力解。优化方法无非是用备忘录或者 DP table，再无奥妙可言。
这个例子的最后，讲一个细节优化。细心的读者会发现，根据斐波那契数列的状态转移方程，当前状态只和之前的两个状态有关，其实并不需要那么长的一个 DP table 来存储所有的状态，只要想办法存储之前的两个状态就行了。所以，可以进一步优化，把空间复杂度降为 O(1)：
int fib(int n) {
if (n < 2) return n;
int prev = 0, curr = 1;
for (int i = 0; i < n - 1; i++) {
int sum = prev + curr;
prev = curr;
curr = sum;
}
return curr;
}
有人会问，动态规划的另一个重要特性「最优子结构」，怎么没有涉及？下面会涉及。斐波那契数列的例子严格来说不算动态规划，以上旨在演示算法设计螺旋上升的过程。当问题中要求求一个最优解或在代码中看到循环和 max、min 等函数时，十有八九，需要动态规划大显身手。
下面，看第二个例子，凑零钱问题，有了上面的详细铺垫，这个问题会很快解决。
题目：给你 k 种面值的硬币，面值分别为 c1, c2 … ck，再给一个总金额 n，问你最少需要几枚硬币凑出这个金额，如果不可能凑出，则回答 -1 。
比如说，k = 3，面值分别为 1，2，5，总金额 n = 11，那么最少需要 3 枚硬币，即 11 = 5 + 5 + 1 。下面走流程。
一、暴力解法
首先是最困难的一步，写出状态转移方程，这个问题比较好写：
动态规划算法/DP - 图8
其实，这个方程就用到了「最优子结构」性质：原问题的解由子问题的最优解构成。即 f(11) 由 f(10), f(9), f(6) 的最优解转移而来。
记住，要符合「最优子结构」，子问题间必须互相独立。啥叫相互独立？你肯定不想看数学证明，我用一个直观的例子来讲解。
比如说，你的原问题是考出最高的总成绩，那么你的子问题就是要把语文考到最高，数学考到最高…… 为了每门课考到最高，你要把每门课相应的选择题分数拿到最高，填空题分数拿到最高…… 当然，最终就是你每门课都是满分，这就是最高的总成绩。
得到了正确的结果：最高的总成绩就是总分。因为这个过程符合最优子结构，“每门科目考到最高”这些子问题是互相独立，互不干扰的。
但是，如果加一个条件：你的语文成绩和数学成绩会互相制约，此消彼长。这样的话，显然你能考到的最高总成绩就达不到总分了，按刚才那个思路就会得到错误的结果。因为子问题并不独立，语文数学成绩无法同时最优，所以最优子结构被破坏。
回到凑零钱问题，显然子问题之间没有相互制约，而是互相独立的。所以这个状态转移方程是可以得到正确答案的。
之后就没啥难点了，按照方程写暴力递归算法即可。如果不太会写递归，参见前文 递归详解。
int coinChange(vector& coins, int amount) {
if (amount == 0) return 0;
int ans = INT_MAX;
for (int coin : coins) {
// 金额不可达
if (amount - coin < 0) continue;
int subProb = coinChange(coins, amount - coin);
// 子问题无解
if (subProb == -1) continue;
ans = min(ans, subProb + 1);
}
return ans == INT_MAX ? -1 : ans;
}
画出递归树：
动态规划算法/DP - 图9
时间复杂度分析：子问题总数 x 每个子问题的时间。子问题总数为递归树节点个数，这个比较难看出来，是 O(n^k)，总之是指数级别的。每个子问题中含有一个 for 循环，复杂度为 O(k)。所以总时间复杂度为 O(kn^k)，指数级别。
*二、带备忘录的递归算法
int coinChange(vector& coins, int amount) {
// 备忘录初始化为 -2
vector memo(amount + 1, -2);
return helper(coins, amount, memo);
}

int helper(vector& coins, int amount, vector& memo) {
if (amount == 0) return 0;
if (memo[amount] != -2) return memo[amount];
int ans = INT_MAX;
for (int coin : coins) {
// 金额不可达
if (amount - coin < 0) continue;
int subProb = helper(coins, amount - coin, memo);
// 子问题无解
if (subProb == -1) continue;
ans = min(ans, subProb + 1);
}
// 记录本轮答案
memo[amount] = (ans == INT_MAX) ? -1 : ans;
return memo[amount];
}
不画图了，很显然「备忘录」大大减小了子问题数目，完全消除了子问题的冗余，所以子问题总数不会超过金额数 n，即子问题数目为 O(n)。处理一个子问题的时间不变，仍是 O(k)，所以总的时间复杂度是 O(kn)。
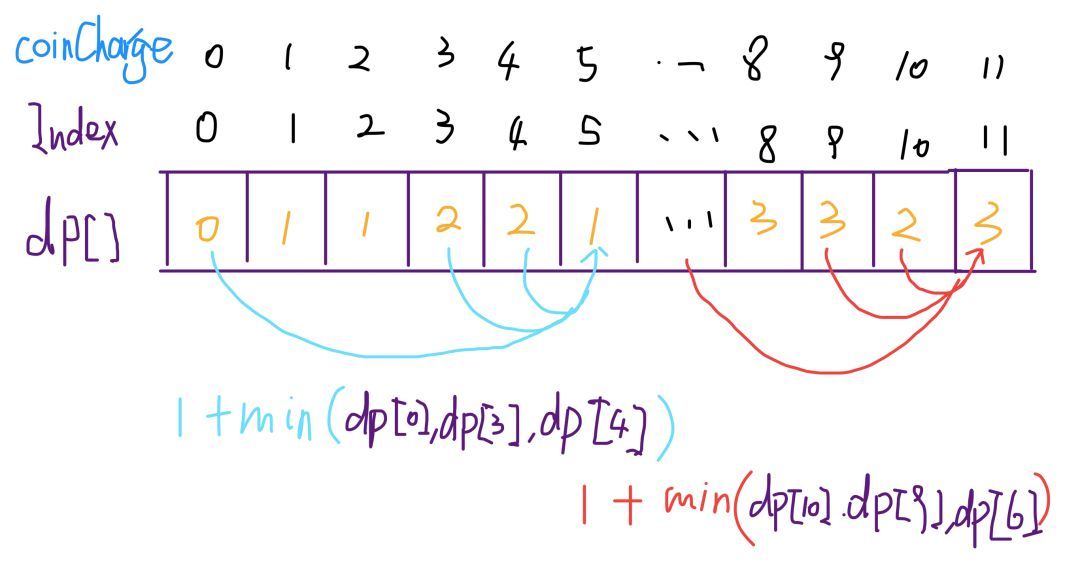
三、动态规划
int coinChange(vector& coins, int amount) {
vector dp(amount + 1, INT_MAX);
dp[0] = 0;
for (int i = 0; i < dp.size(); i++) {
// 内层 for 在求所有子问题 + 1 的最小值
for (int coin : coins) {
if (i - coin < 0) continue;
dp[i] = min(dp[i], 1 + dp[i - coin]);
}
}
return dp[amount] == INT_MAX ? -1 : dp[amount];
}
动态规划算法/DP - 图10
最后总结
如果你不太了解动态规划，还能看到这里，真得给你鼓掌，相信你已经掌握了这个算法的设计技巧。
计算机解决问题其实没有任何奇技淫巧，它唯一的解决办法就是穷举，穷举所有可能性。算法设计无非就是先思考“如何穷举”，然后再追求“如何聪明地穷举”。
列出动态转移方程，就是在解决“如何穷举”的问题。之所以说它难，一是因为很多穷举需要递归实现，二是因为有的问题本身的解空间复杂，不那么容易穷举完整。
备忘录、DP table 就是在追求“如何聪明地穷举”。用空间换时间的思路，是降低时间复杂度的不二法门，除此之外，试问，还能玩出啥花活？

棍子切割

如果木棒的长度为8，不同部分的值如下所示，则可获得的最大值为22（通过切割两段长度2和6）、
长度 1 2 3 4 5 6 7 8
价值 1 5 8 9 10 17 17 20 
  1. public class RodCutting {
  2.     // A Naive recursive solution for Rod cutting problem
  3.     /*
  4.      * Returns the best obtainable price for a rod of length n and price[] as prices
  5.      * of different pieces
  6.      */
  7.     static int cutRod(int price[], int n) {
  8.         if (n <= 0)
  9.             return 0;
  10.         int max_val = Integer.MIN_VALUE;
  12.         // Recursively cut the rod in different pieces and
  13.         // compare different configurations
  14.         for (int i = 0; i < n; i++)
  15.             max_val = Math.max(max_val, price[i] + cutRod(price, n - i - 1));
  17.         return max_val;
  18.     }
  20.     /* Driver program to test above functions */
  21.     public static void main(String args[]) {
  22.         int arr[] = new int[] { 1, 5, 8, 9, 10, 17, 17, 20 };
  23.         int size = arr.length;
  24.         System.out.println("Maximum Obtainable Value is " + cutRod(arr, size));
  26.     }
  27. }

有许多子问题是反复解决的。由于再次调用了相同的父问题，所以这个问题具有重叠的子族属性。因此，切割木棒问题具有动态规划问题的两个性质。与其他典型的动态规划（DP）问题一样，可以通过自下而上构造dp[]数组来避免相同子问题重复计算。

  1. public class RodCutting2 {
  2.     /*
  3.      * A Dynamic Programming solution for Rod cutting problem
  4.      * Returns the best obtainable price for a rod of length n and price[] as prices
  5.      * of different pieces
  6.      */
  7.     static int cutRod(int price[], int n) {
  8.         int val[] = new int[n + 1];
  9.         val[0] = 0;
  11.         // Build the table val[] in bottom up manner and return
  12.         // the last entry from the table
  13.         for (int i = 1; i <= n; i++) {
  14.             int max_val = Integer.MIN_VALUE;
  15.             for (int j = 0; j < i; j++)
  16.                 max_val = Math.max(max_val, price[j] + val[i - j - 1]);
  17.             val[i] = max_val;
  18.         }
  20.         return val[n];
  21.     }
  23.     /* Driver program to test above functions */
  24.     public static void main(String args[]) {
  25.         int arr[] = new int[] { 1, 5, 8, 9, 10, 17, 17, 20 };
  26.         int size = arr.length;
  27.         System.out.println("Maximum Obtainable Value is " + cutRod(arr, size));
  28.     }
  29. }

参考

https://leetcode-cn.com/problems/coin-change/solution/dong-tai-gui-hua-tao-lu-xiang-jie-by-wei-lai-bu-ke/
https://juejin.im/post/5dcb8201e51d45210f046f5a
https://leetcode-cn.com/problems/unique-binary-search-trees/solution/bu-tong-de-er-cha-sou-suo-shu-by-leetcode/
https://blog.csdn.net/weixin_40446252/article/details/104164306