递归

104. 二叉树的最大深度

https://leetcode-cn.com/problems/maximum-depth-of-binary-tree/
给定一个二叉树，找出其最大深度。
二叉树的深度为根节点到最远叶子节点的最长路径上的节点数。
说明: 叶子节点是指没有子节点的节点。
示例：
给定二叉树 [3,9,20,null,null,15,7]，
3
/ \
9 20
/ \
15 7
返回它的最大深度 3 。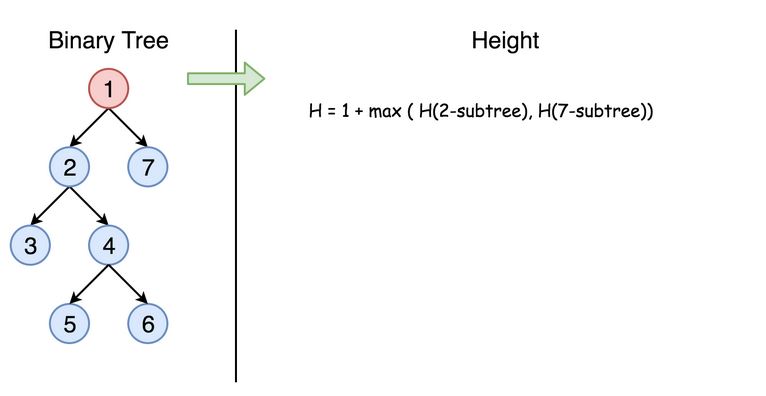









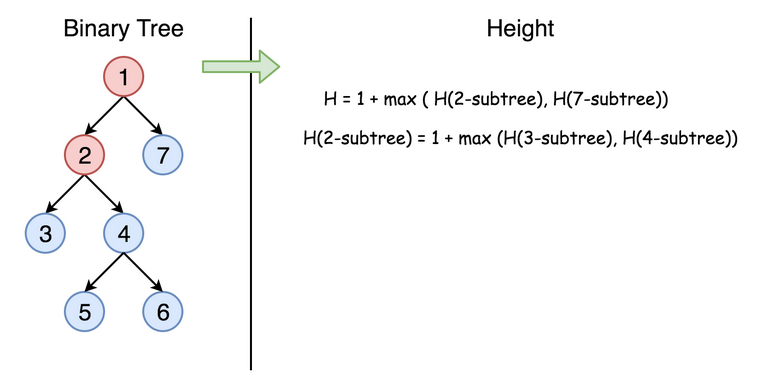
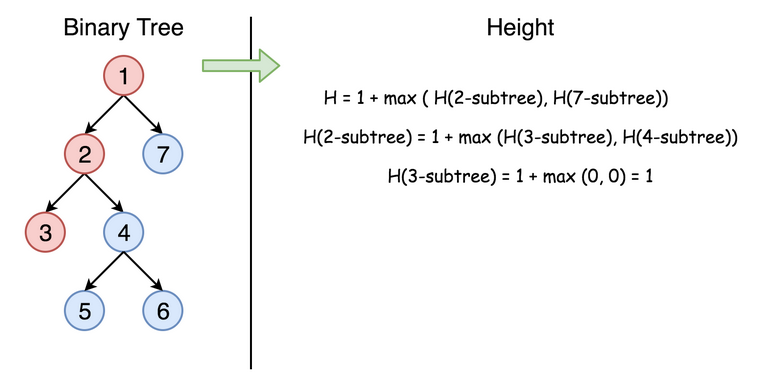
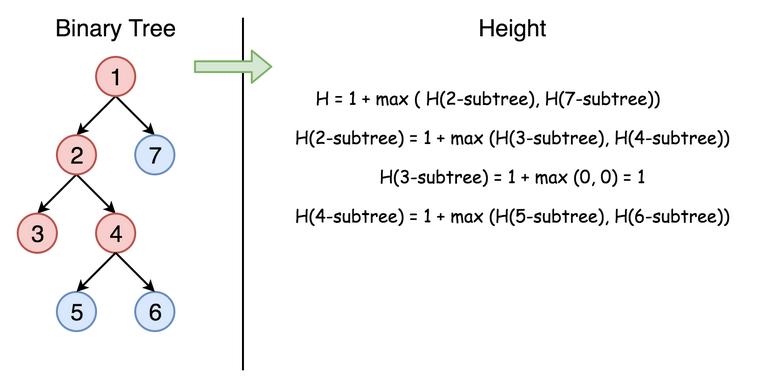
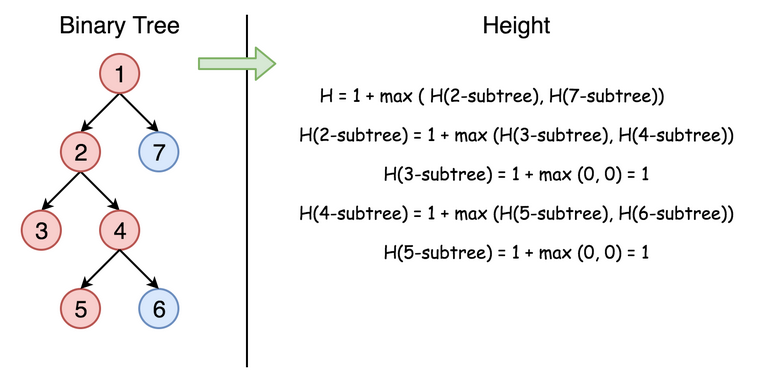
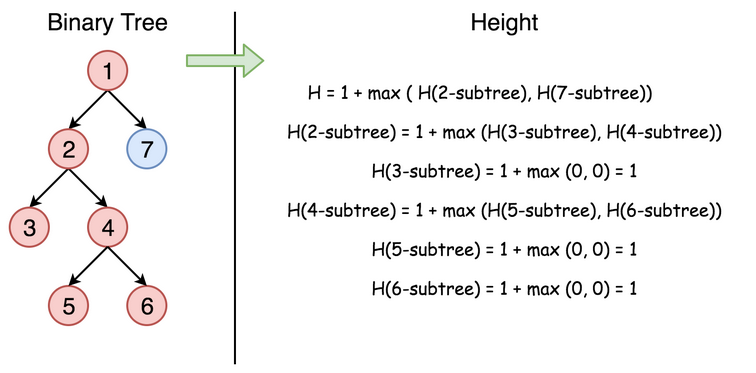
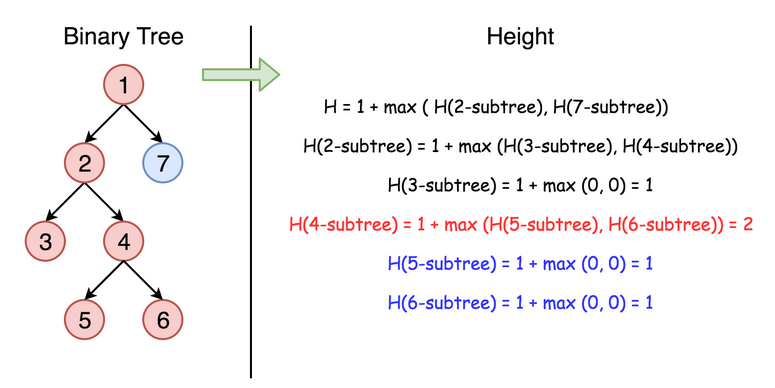
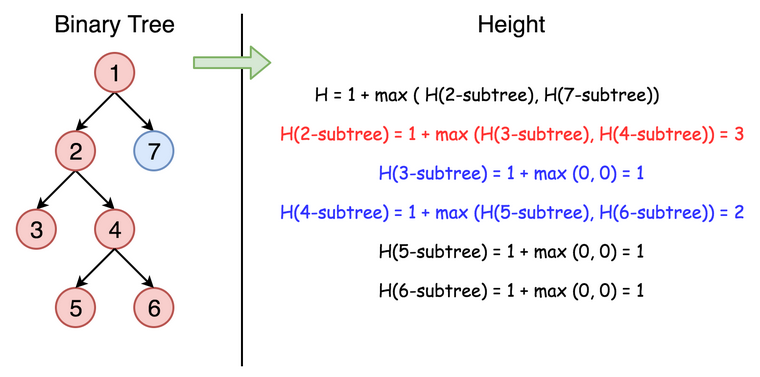
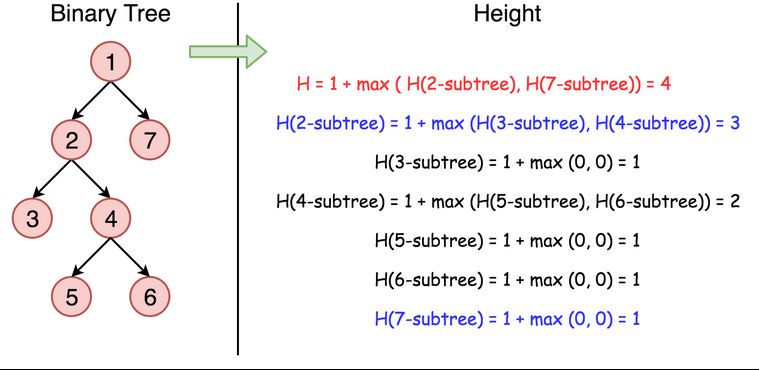
个节点的深度与它左右子树的深度有关，且等于其左右子树最大深度值加上 1。即：
maxDepth(root) = max(maxDepth(root.left), maxDepth(root.right)) + 1

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode(int x) { val = x; }
 * }
 */
class Solution {
    public int maxDepth(TreeNode root) {
         if (root==null){
            return 0;
        }
        return Math.max(maxDepth(root.left),maxDepth(root.right))+1;
    }
}

时间复杂度：我们每个结点只访问一次，因此时间复杂度为 O(N)O(N)O(N)，
其中 NNN 是结点的数量。
空间复杂度：在最糟糕的情况下，树是完全不平衡的，例如每个结点只剩下左子结点，递归将会被调用 NNN 次（树的高度），因此保持调用栈的存储将是 O(N)O(N)O(N)。但在最好的情况下（树是完全平衡的），树的高度将是 log⁡(N)\log(N)log(N)。因此，在这种情况下的空间复杂度将是 O(log⁡(N))O(\log(N))O(log(N))。

206. 反转链表

class Solution {
    public ListNode reverseList(ListNode head) {
        //递归终止条件是当前为空，或者下一个节点为空
        if(head==null || head.next==null) {
            return head;
        }
        //这里的cur就是最后一个节点
        ListNode cur = reverseList(head.next);
        //这里请配合动画演示理解
        //如果链表是 1->2->3->4->5，那么此时的cur就是5
        //而head是4，head的下一个是5，下下一个是空
        //所以head.next.next 就是5->4
        head.next.next = head;
        //防止链表循环，需要将head.next设置为空
        head.next = null;
        //每层递归函数都返回cur，也就是最后一个节点
        return cur;
    }
}