概述

二叉搜索树(Binary Search Tree,BST),也称为二叉排序树或二叉查找树。
非空的二叉搜索树有如下性质：

  1. 非空左子树左子树上所有的节点的值都小于它的根节点的值。
  2. 非空左子树右子树上所有的节点的值均大于它的根节点的值。
  3. 左右子树均为二叉搜索树；

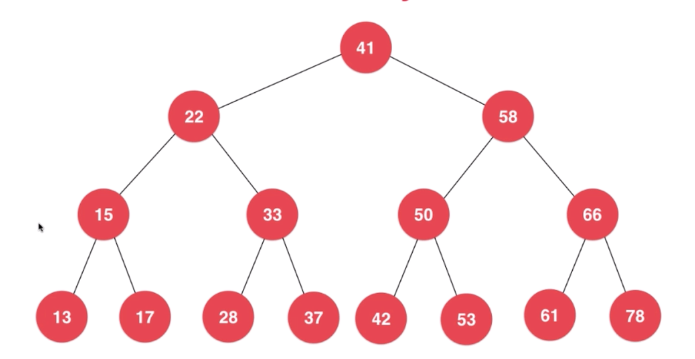
图片.png

二分搜索树 递归实现

  1. public void add(E e){
  2.         root = add(root,e);
  3.     }
  5.     /**
  6.      * 二分搜索树插入元素 递归实现
  7.      */
  8.     private Node add(Node node ,E e){
  9.         if (node==null){
  10.             size++;
  11.             return new Node(e);
  12.         }
  13.         if (e.compareTo(node.data)<0){
  14.            node.left = add(node.left,e);
  15.         }else if (e.compareTo(node.data)>0){
  16.             node.right = add(node.right,e);
  17.         }
  18.         return node;
  19.     }

二分搜索树 查找递归实现

  1. public boolean contains(E e){
  2.         return contains(root, e);
  3.     }
  4.     private boolean contains(Node node,E e){
  5.         if (node==null){
  6.             return false;
  7.         }if (e.compareTo(node.data)==0){
  8.             return true;
  9.         }else if(e.compareTo(node.data)<0){
  10.             return contains(node.left,e);
  11.         }else {
  12.             return contains(node.right,e);
  13.         }
  14.     }

二叉搜索树一定程度上可以提高搜索效率，但是当原序列有序时，例如序列 A = {1，2，3，4，5，6}，构造二叉搜索树如图 1.1。依据此序列构造的二叉搜索树为右斜树，同时二叉树退化成单链表，搜索效率降低为 O(n)。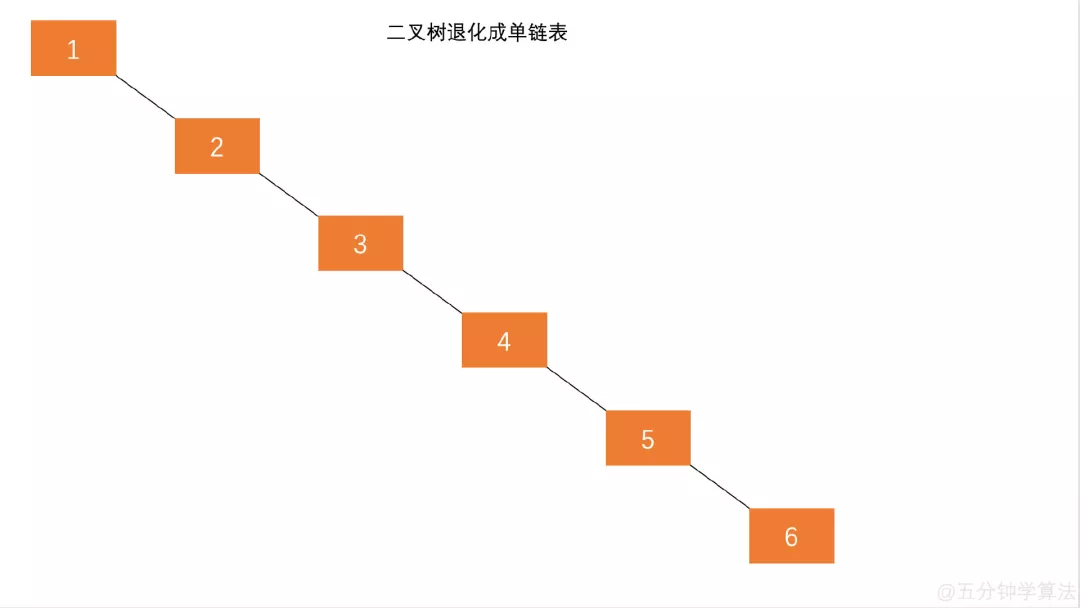
平衡二叉树（AVL） - 图2
二叉搜索树的查找效率取决于树的高度，因此保持树的高度最小，即可保证树的查找效率。

概念

平衡二叉查找树：简称平衡二叉树。由前苏联的数学家 Adelse-Velskil 和 Landis 在 1962 年提出的高度平衡的二叉树，根据科学家的英文名也称为 AVL 树。它具有如下几个性质：

  1. 可以是空树。
  2. 假如不是空树，任何一个节点的左子树与右子树都是平衡二叉树，并且高度之差的绝对值不超过 1。

二叉树调整

参考

https://www.jianshu.com/p/88f15de56257