Summary
- 归一化简单来说就是将训练集中某一列数值特征的值缩放到 0 和 1 之间。
- 标准化就是将训练集中某一列数值特征的值缩放成均值为 0,方差为 1 的状态。
- 注意1:归一化和标准化的相同点都是对某个特征(column)进行缩放(scaling)而不是对某个样本的特征向量(row)进行缩放。
- 注意2:在线性代数中,将一个向量除以向量的长度,也被称为标准化,即 Scaling to unit length。不过这里的标准化是将向量变为长度为 1 的单位向量,它和我们这里的标准化不是一回事。
Methods
Rescaling (min-max normalization)
Also known as min-max scaling or min-max normalization, is the simplest method and consists in rescaling the range of features to scale the range in [0, 1] or [−1, 1]. Selecting the target range depends on the nature of the data. The general formula for a min-max of [0, 1] is given as:
%20%7D%7B%20max(x)-min(x)%20%7D%20%0A#card=math&code=x%27%3D%5Cfrac%20%7B%20x-min%28x%29%20%7D%7B%20max%28x%29-min%28x%29%20%7D%20%0A&height=37&width=139)
where an original value,
is the normalized value. For example, suppose that we have the students’ weight data, and the students’ weights span [160 pounds, 200 pounds]. To rescale this data, we first subtract 160 from each student’s weight and divide the result by 40 (the difference between the maximum and minimum weights).
To rescale a range between an arbitrary set of values [a, b], the formula becomes:
)(b-a)%20%7D%7B%20max(x)-min(x)%20%7D%20%0A#card=math&code=x%27%3Da%2B%5Cfrac%20%7B%20%28x-min%28x%29%29%28b-a%29%20%7D%7B%20max%28x%29-min%28x%29%20%7D%20%0A&height=37&width=176)
where are the min-max values.
Mean normalization
%20%7D%7B%20max(x)-min(x)%20%7D%0A#card=math&code=x%27%3D%5Cfrac%20%7B%20x-mean%28x%29%20%7D%7B%20max%28x%29-min%28x%29%20%7D%0A&height=37&width=139)
where is an original value,
is the normalized value. There is another form of the mean normalization which is when we divide by the standard deviation which is also called standardization.
Standardization (Z-score Normalization)
In machine learning, we can handle various types of data, e.g. audio signals and pixel values for image data, and this data can include multiple dimensions. Feature standardization makes the values of each feature in the data have zero-mean (when subtracting the mean in the numerator) and unit-variance. This method is widely used for normalization in many machine learning algorithms (e.g., support vector machines, logistic regression, and artificial neural networks)[2][citation needed]. The general method of calculation is to determine the distribution mean and standard deviation for each feature. Next we subtract the mean from each feature. Then we divide the values (mean is already subtracted) of each feature by its standard deviation.
Where is the original feature vector,
#card=math&code=%5Cbar%7Bx%7D%3Dmean%28x%29&height=16&width=78) is the mean of that feature vector, and $\sigma $ is its standard deviation.
Scaling to unit length
Another option that is widely used in machine-learning is to scale the components of a feature vector such that the complete vector has length one. This usually means dividing each component by the Euclidean lengthof the vector:
In some applications (e.g. Histogram features) it can be more practical to use the L1 norm (i.e. Manhattan Distance, City-Block Length or Taxicab Geometry) of the feature vector. This is especially important if in the following learning steps the Scalar Metric is used as a distance measure.
Motivation
Since the range of values of raw data varies widely, in some machine learningalgorithms, objective functions will not work properly without normalization). For example, many classifierscalculate the distance between two points by the Euclidean distance. If one of the features has a broad range of values, the distance will be governed by this particular feature. Therefore, the range of all features should be normalized so that each feature contributes approximately proportionately to the final distance.
Another reason why feature scaling is applied is that gradient descentconverges much faster with feature scaling than without it.[1]
提升模型精度
在机器学习算法的目标函数(例如 SVM 的 RBF 内核或线性模型的 l1 和 l2 正则化),许多学习算法中目标函数的基础都是假设所有的特征都是零均值并且具有同一阶数上的方差。如果某个特征的方差比其他特征大几个数量级,那么它就会在学习算法中占据主导位置,导致学习器并不能像我们说期望的那样,从其他特征中学习。
举一个简单的例子,在 KNN 中,我们需要计算待分类点与所有实例点的距离。假设每个实例点(instance)由 n 个 features 构成。如果我们选用的距离度量为欧式距离,如果数据预先没有经过归一化,那么那些绝对值大的 features 在欧式距离计算的时候起了决定性作用。
从经验上说,归一化是让不同维度之间的特征在数值上有一定比较性,可以大大提高分类器的准确性。
提升收敛速度
对于线性模型来说,数据归一化后,最优解的寻优过程明显会变得平缓,更容易正确的收敛到最优解。
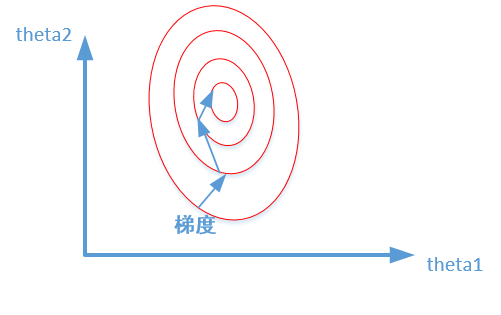
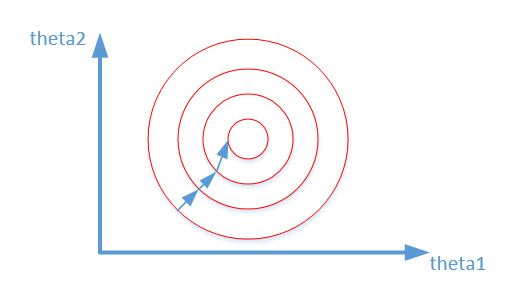
比较这两个图,前者是没有经过归一化的,在梯度下降的过程中,走的路径更加的曲折,而第二个图明显路径更加平缓,收敛速度更快。 对于神经网络模型,避免饱和是一个需要考虑的因素,通常参数的选择决定于input数据的大小范围。
Comparation
首先明确,在机器学习中,标准化是更常用的手段,归一化的应用场景是有限的。我总结原因有两点:
- 标准化更好保持了样本间距。当样本中有异常点时,归一化有可能将正常的样本“挤”到一起去。比如三个样本,某个特征的值为1,2,10000,假设10000这个值是异常值,用归一化的方法后,正常的1,2就会被“挤”到一起去。如果不幸的是1和2的分类标签还是相反的,那么,当我们用梯度下降来做分类模型训练时,模型会需要更长的时间收敛,因为将样本分开需要更大的努力!而标准化在这方面就做得很好,至少它不会将样本“挤到一起”。
- 标准化更符合统计学假设。
对一个数值特征来说,很大可能它是服从正态分布的。标准化其实是基于这个隐含假设,只不过是略施小技,将这个正态分布调整为均值为0,方差为1的标准正态分布而已。
所以,下面的讨论我们先集中分析标准化在机器学习中运用的情况,在文章末尾,简单探讨一下归一化的使用场景。这样更能凸显重点,又能保持内容的完整性。
Application of Standardization
回答完上面的问题,就可以很好地掌握标准化在机器学习中的运用。
Q:逻辑斯蒂回归是否必须使用标准化?
真正的答案是,这取决于我们的逻辑回归是不是用正则。
如果你不用正则,那么,标准化并不是必须的,如果你用正则,那么标准化是必须的。不用正则时,我们的损失函数只是仅仅在度量预测与真实的差距,加上正则后,我们的损失函数除了要度量上面的差距外,还要度量参数值是否足够小。而参数值的大小程度或者说大小的级别是与特征的数值范围相关的。
举例来说,我们用体重预测身高 ,体重
用
衡量时,训练出的模型是:
,
就是我们训练出来的参数。当我们的体重用
来衡量时,
的值就会扩大为原来的 1000 倍。在上面两种情况下,都用 L1 正则的话,显然对模型的训练影响是不同的。
假如不同的特征的数值范围不一样,有的是 0 到 0.1,有的是 100 到 10000,那么,每个特征对应的参数大小级别也会不一样,在L1正则时,我们是简单将参数的绝对值相加,因为它们的大小级别不一样,就会导致L1最后只会对那些级别比较大的参数有作用,那些小的参数都被忽略了。
Q:如果不用正则,那么标准化对逻辑回归有什么好处吗?
答案是有好处,进行标准化后,我们得出的参数值的大小可以反应出不同特征对样本 label 的贡献度,方便我们进行特征筛选。如果不做标准化,是不能这样来筛选特征的。
Q:做标准化有什么注意事项吗?
最大的注意事项就是先拆分出 test 集,不要在整个数据集上做标准化,因为那样会将 test 集的信息引入到训练集中,这是一个非常容易犯的错误!
Q:决策树需要标准化吗,为什么?
不需要标准化。因为决策树中的切分依据,信息增益、信息增益比、Gini指数都是基于概率得到的,和值的大小没有关系。另外同属概率模型的朴素贝叶斯,隐马尔科夫也不需要标准化。
另外 如果是训练神经网络,标准化后,收敛会更快
Application of Normalization
有时候,我们必须要特征在0到1之间,此时就只能用归一化。有种svm可用来做单分类,里面就需要用到归一化,由于没有深入研究,所以我把链接放上,感兴趣的可以自己看。
http://citeseerx.ist.psu.edu/viewdoc/summary?doi=10.1.1.100.2524
Rerefences
https://en.wikipedia.org/wiki/Feature_scaling https://en.wikipedia.org/wiki/Normalization_(statistics)) https://blog.csdn.net/zwqjoy/article/details/81182102 https://www.jianshu.com/p/1e63cd2afedc https://www.jianshu.com/p/4c3081d40ca6 https://scikit-learn.org/stable/modules/generated/sklearn.preprocessing.Normalizer.html

