1 最大流问题

1.1 记号简记

无向图

#card=math&code=G%3D%28V%2CE%29&height=16&width=65)，顶点集合 ，边集合 ，边 。

有向图

#card=math&code=D%3D%28V%2CA%29&height=16&width=66)，顶点集合 ，弧集合 ，弧 #card=math&code=%28v_i%2Cv_j%29&height=17&width=39)。

图的支撑树

由图的 个节点与 条边组成的树为图的支撑树。

以下例介绍求最小支撑树的两种方法：

1.2 避圈法

，令 ，从 中选最小权边 ；

，从 中选最小权边 ， 且 #card=math&code=%28v%2CE_1%5Ccup%5C%7B%5Bv_2%2Cv_4%5D%5C%7D%29&height=16&width=107) 不含圈，令 ；

，从 中选最小权边 ， 且 #card=math&code=%28v%2CE_2%5Ccup%5C%7B%5Bv_4%2Cv_5%5D%5C%7D%29&height=16&width=107) 不含圈，令 ；

，从 中选最小权边 ， 且 #card=math&code=%28v%2CE_3%5Ccup%5C%7B%5Bv_5%2Cv_6%5D%5C%7D%29&height=16&width=107) 不含圈，令 ；

，从 中选最小权边 ， 且 #card=math&code=%28v%2CE_4%5Ccup%5C%7B%5Bv_1%2Cv_2%5D%5C%7D%29&height=16&width=107) 不含圈，令 ；

，任一条未选边都与已选边构成圈，接待终止， ，

#card=math&code=%28v%2CE_5%29&height=16&width=39) 就是最小支撑树。

1.3 破圈法

取圈 #card=math&code=%28v_1%2Cv_2%2Cv_3%2Cv_1%29&height=16&width=79)，边 的权最大，去掉 ；

取圈 #card=math&code=%28v_3%2Cv_5%2Cv_2%2Cv_3%29&height=16&width=79)，边 的权最大，去掉 ；

取圈 #card=math&code=%28v_3%2Cv_5%2Cv_4%2Cv_2%2Cv_3%29&height=16&width=98)，边 的权最大，去掉 ；

取圈 #card=math&code=%28v_5%2Cv_6%2Cv_4%2Cv_5%29&height=16&width=79)，边 的权最大，去掉 ，得到不含圈的图，即为最小支撑树。

2 最短路

2.1 Dijkstra 标号法

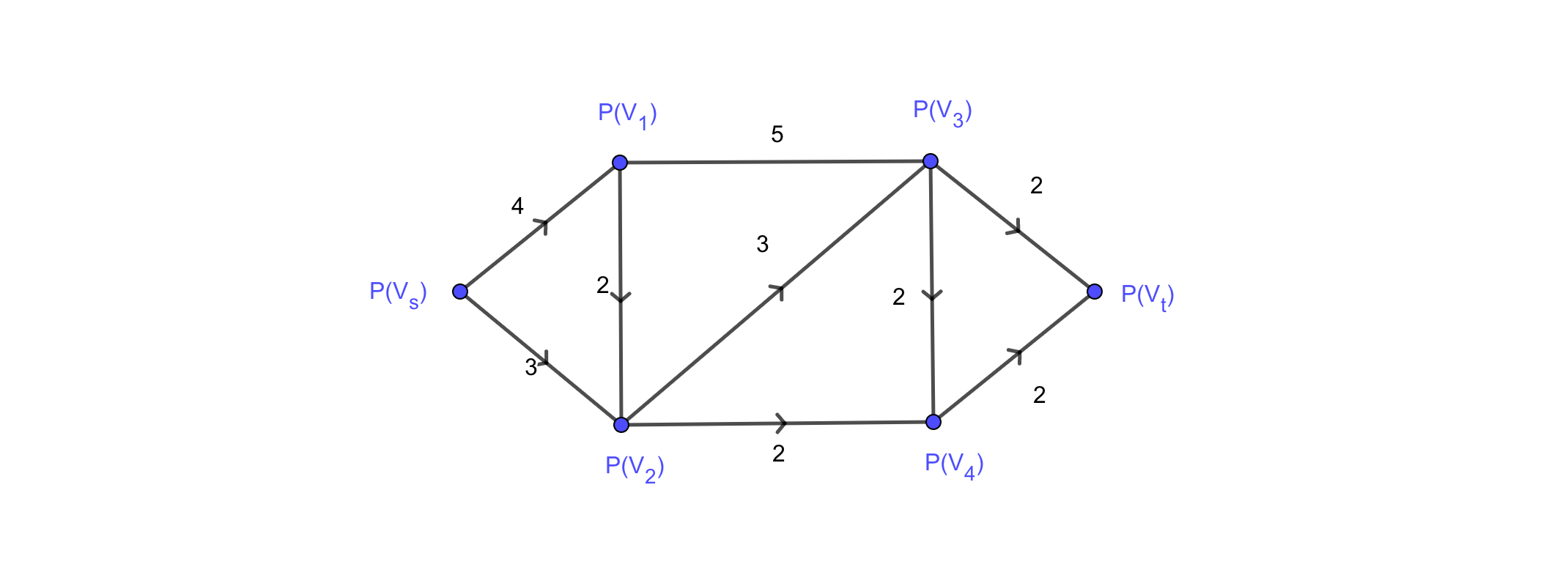
• 适用于求 的最短路，权非负。
• 步骤：

1. 令 ，令
2. ，令
3. %3Dmin%5C%7B6%2C9%5C%7D%3D6#card=math&code=T%28V_3%29%3Dmin%5C%7B6%2C9%5C%7D%3D6&height=16&width=135)，令
4. ，令
5. %3Dmin%5C%7B7%2C8%5C%7D%3D7#card=math&code=T%28V_t%29%3Dmin%5C%7B7%2C8%5C%7D%3D7&height=16&width=133)，令
6. 故最短路为：#card=math&code=%28V_s%2CV_2%2CV_4%2CV_t%29&height=16&width=82)

2.2 逐次逼近法

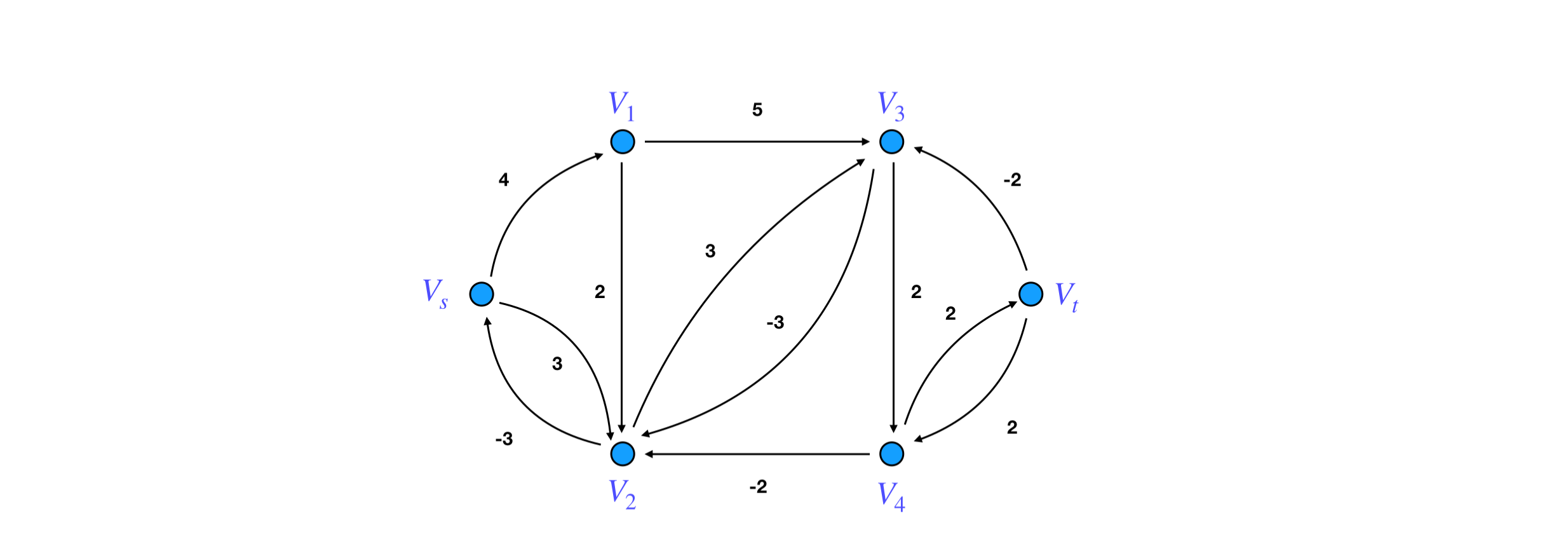
• 适用于求 到任意一点的最短路。
• 权可负。

%7D%20%26%20p%7Bij%7D%5E%7B(2)%7D%20%26%20p%7Bij%7D%5E%7B(3)%7D%20%26%20p%7Bij%7D%5E%7B(4)%7D%20%26%20p%7Bij%7D%5E%7B(5)%7D%5C%5C%0AVs%20%26%200%20%26%204%20%26%203%20%26%20%26%20%26%20%26%200%20%26%200%20%26%200%20%26%200%20%26%200%5C%5C%20%20%0AV_1%20%26%20%20%26%200%20%26%202%20%26%205%20%26%20%26%20%26%204%20%26%204%20%26%204%20%26%204%20%26%204%5C%5C%0AV_2%20%26%20-3%20%26%20%20%26%200%20%26%20%5Cunderline%20%7B3%7D%20%20%26%20%26%20%26%203%20%26%203%20%26%203%20%26%203%20%26%203%5C%5C%20%0AV_3%20%26%20%20%26%20%20%26%20-3%20%26%200%20%26%20%5Cunderline%20%7B2%7D%20%20%26%20%26%20%20%26%20%5Cunderline%20%7B6%7D%20%20%26%206%20%26%206%20%26%206%5C%5C%20%0AV_4%20%26%20%20%26%20%20%26%20-2%20%26%20%26%200%20%26%20%5Cunderline%20%7B2%7D%20%20%26%20%20%26%20%20%26%20%5Cunderline%20%7B8%7D%20%20%26%208%20%26%208%5C%5C%20%0AV_t%20%26%20%20%26%20%20%26%20%20%26%20-2%20%26%20-2%20%26%200%20%26%20%20%26%20%20%26%20%20%26%20%5Cunderline%20%7B10%7D%20%20%26%2010%5C%5C%20%0A%5Cend%7Bmatrix%7D%0A#card=math&code=%5Cbegin%7Bmatrix%7D%0A%20%20%26%20%20V_s%20%26%20V_1%20%26%20V_2%20%26%20V_3%20%26%20V_4%20%26%20V_t%20%26%20p%7Bij%7D%5E%7B%281%29%7D%20%26%20p%7Bij%7D%5E%7B%282%29%7D%20%26%20p%7Bij%7D%5E%7B%283%29%7D%20%26%20p%7Bij%7D%5E%7B%284%29%7D%20%26%20p%7Bij%7D%5E%7B%285%29%7D%5C%5C%0AV_s%20%26%200%20%26%204%20%26%203%20%26%20%26%20%26%20%26%200%20%26%200%20%26%200%20%26%200%20%26%200%5C%5C%20%20%0AV_1%20%26%20%20%26%200%20%26%202%20%26%205%20%26%20%26%20%26%204%20%26%204%20%26%204%20%26%204%20%26%204%5C%5C%0AV_2%20%26%20-3%20%26%20%20%26%200%20%26%20%5Cunderline%20%7B3%7D%20%20%26%20%26%20%26%203%20%26%203%20%26%203%20%26%203%20%26%203%5C%5C%20%0AV_3%20%26%20%20%26%20%20%26%20-3%20%26%200%20%26%20%5Cunderline%20%7B2%7D%20%20%26%20%26%20%20%26%20%5Cunderline%20%7B6%7D%20%20%26%206%20%26%206%20%26%206%5C%5C%20%0AV_4%20%26%20%20%26%20%20%26%20-2%20%26%20%26%200%20%26%20%5Cunderline%20%7B2%7D%20%20%26%20%20%26%20%20%26%20%5Cunderline%20%7B8%7D%20%20%26%208%20%26%208%5C%5C%20%0AV_t%20%26%20%20%26%20%20%26%20%20%26%20-2%20%26%20-2%20%26%200%20%26%20%20%26%20%20%26%20%20%26%20%5Cunderline%20%7B10%7D%20%20%26%2010%5C%5C%20%0A%5Cend%7Bmatrix%7D%0A&height=143&width=366)

故 到 最短路为：#card=math&code=%28V_s%2CV_2%2CV_3%2CV_4%2CV_t%29&height=16&width=102)，最短路权为 10。

2.3 Floyd 法

• 算法核心：%7D%3Dmin%5C%7Bd%7Bij%7D%5E%7B(k)%7D%2Cd%7Bik%7D%5E%7B(k)%7D%2Bd%7Bkj%7D%5E%7B(k)%7D%5C%7D#card=math&code=d%7Bij%7D%5E%7B%28k%2B1%29%7D%3Dmin%5C%7Bd%7Bij%7D%5E%7B%28k%29%7D%2Cd%7Bik%7D%5E%7B%28k%29%7D%2Bd_%7Bkj%7D%5E%7B%28k%29%7D%5C%7D&height=23&width=174)
• 适用于求图中任意两点间最短距离。
• 建造银行、医院等问题。
• 除下面的例子，其他应用举例请参考【P311】。

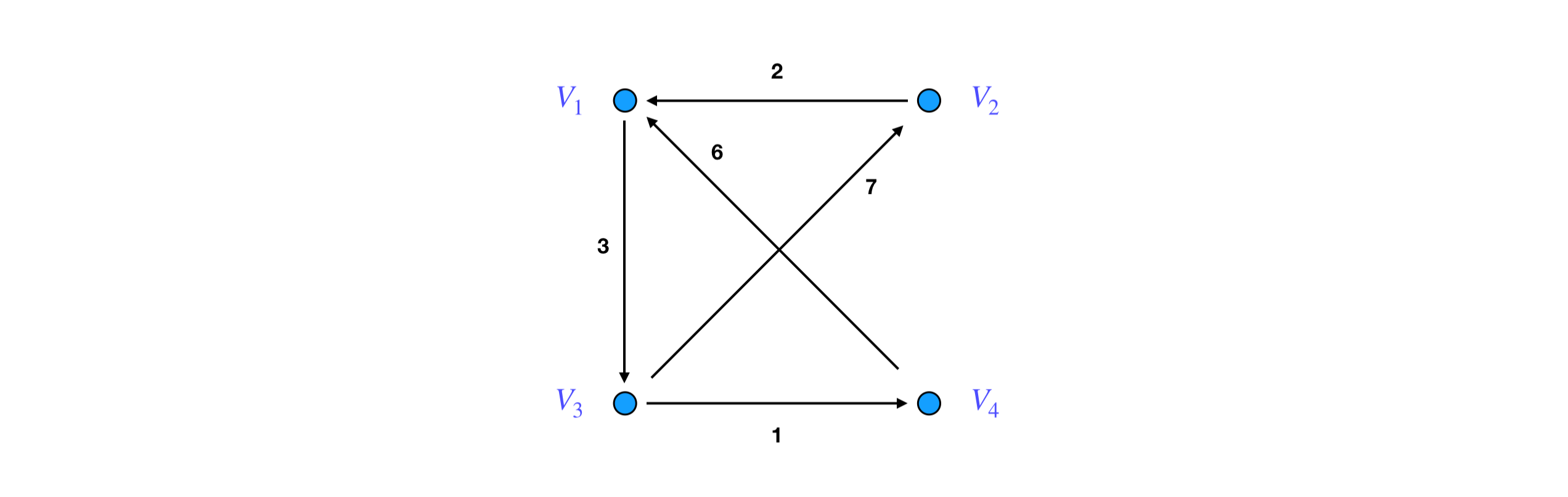
求解：

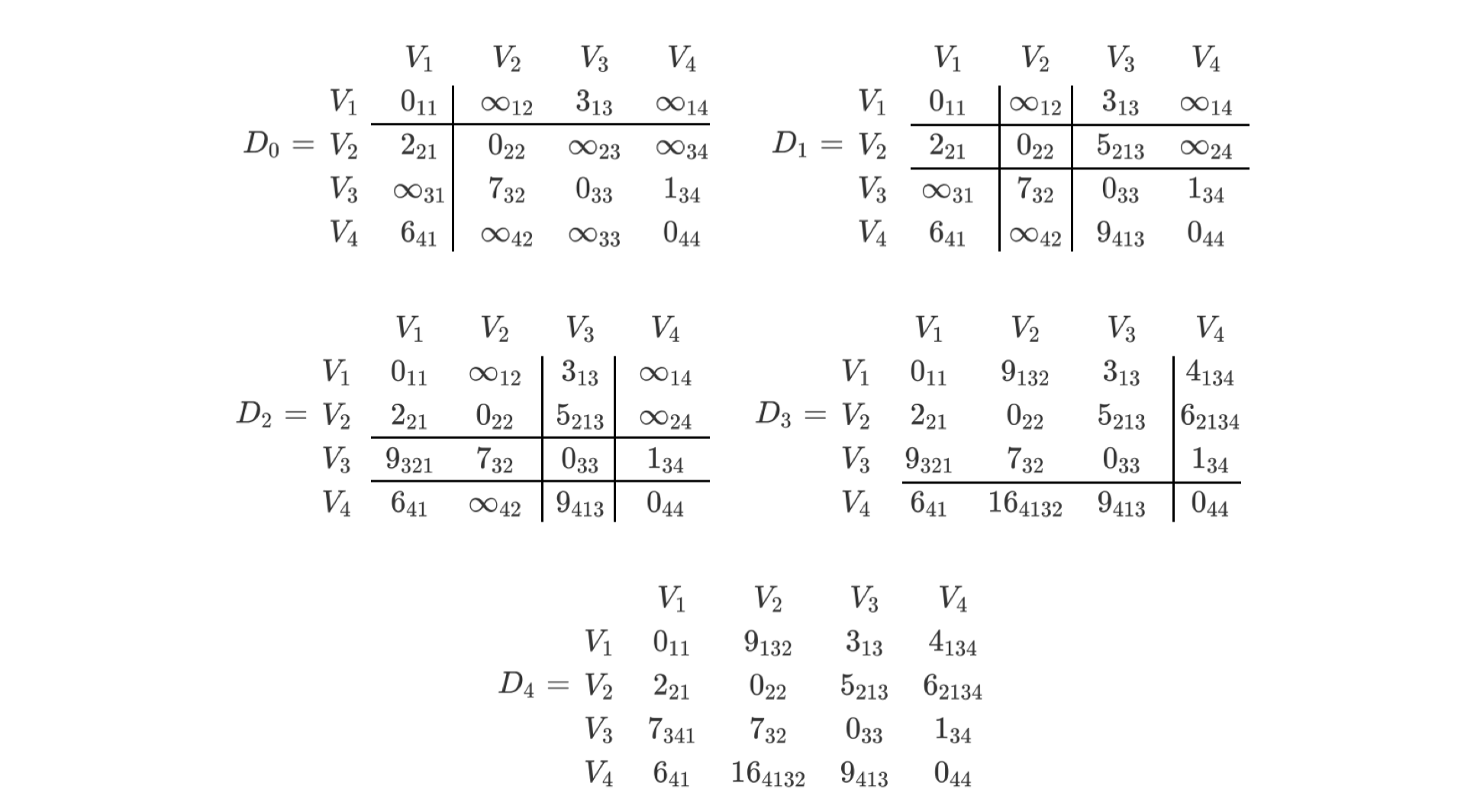
3 最大流问题

3.1 网络与流

• 给定一个有向图 #card=math&code=D%3D%28V%2CA%29&height=16&width=66)，在 中指定了两个点，发点 和收点 ，其余的点为中间点。%5Cin%20A#card=math&code=%28Vi%2CV_j%29%5Cin%20A&height=17&width=69)，均对应有一个数  （容量），则称 为一个网络 #card=math&code=D%3D%28V%2CA%2CC%29&height=16&width=82)， 为容量集合。
• #card=math&code=f%3D%5C%7Bf%28vi%2Cv_j%5C%7D%2Cf%7Bij%7D%3Df%28v_i%2Cv_j%29&height=17&width=167) 是弧 #card=math&code=%28v_i%2Cv_j%29&height=17&width=39) 上的流量。

3.2 可行流与最大流

可行流

可行流为满足以下两个条件的流 ：

1. 容量限制条件：对每一条弧 #card=math&code=%28vi%2Cv_j%5Cin%20A%29&height=17&width=66)，有 
2. 平衡条件：

%20%7D%7B%20f%7B%20ij%20%7D%20%7D%20-%5Csum%20%7B%20(v%7B%20j%20%7D%2Cv%7B%20i%20%7D)%20%7D%7B%20f%7B%20ji%20%7D%20%7D%20%3D0%2Ci%5Cneq%20s%2Ct%5C%5C%0A%5Csum%20%7B%20(v%7B%20s%7D%2Cv%7B%20j%20%7D)%20%7D%7B%20f%7B%20sj%20%7D%20%7D%20-%5Csum%20%7B%20(v%7B%20j%20%7D%2Cv%7B%20s%20%7D)%20%7D%7B%20f%7B%20js%20%7D%20%7D%20%3Dv(f)%2Ci%20%3Ds%5C%5C%0A%5Csum%20%7B%20(v%7B%20t%7D%2Cv%7B%20j%20%7D)%20%7D%7B%20f%7B%20tj%20%7D%20%7D%20-%5Csum%20%7B%20(v%7B%20j%20%7D%2Cv%7B%20t%20%7D)%20%7D%7B%20f%7B%20jt%20%7D%20%7D%20%3D-v(f)%2Ci%20%3Dt%0A#card=math&code=%5Csum%20%7B%20%28v%7B%20i%20%7D%2Cv%7B%20j%20%7D%29%20%7D%7B%20f%7B%20ij%20%7D%20%7D%20-%5Csum%20%7B%20%28v%7B%20j%20%7D%2Cv%7B%20i%20%7D%29%20%7D%7B%20f%7B%20ji%20%7D%20%7D%20%3D0%2Ci%5Cneq%20s%2Ct%5C%5C%0A%5Csum%20%7B%20%28v%7B%20s%7D%2Cv%7B%20j%20%7D%29%20%7D%7B%20f%7B%20sj%20%7D%20%7D%20-%5Csum%20%7B%20%28v%7B%20j%20%7D%2Cv%7B%20s%20%7D%29%20%7D%7B%20f%7B%20js%20%7D%20%7D%20%3Dv%28f%29%2Ci%20%3Ds%5C%5C%0A%5Csum%20%7B%20%28v%7B%20t%7D%2Cv%7B%20j%20%7D%29%20%7D%7B%20f%7B%20tj%20%7D%20%7D%20-%5Csum%20%7B%20%28v%7B%20j%20%7D%2Cv%7B%20t%20%7D%29%20%7D%7B%20f_%7B%20jt%20%7D%20%7D%20%3D-v%28f%29%2Ci%20%3Dt%0A&height=115&width=583)

• #card=math&code=v%28f%29&height=16&width=24) 为可行流流量 发点净输出量或收点净输入量。
• 可行流总存在，即零流，%3D0%2Cf%7Bij%7D%3D0#card=math&code=v%28f%29%3D0%2Cf%7Bij%7D%3D0&height=17&width=95)

最大流问题——数学模型

最大流问题本质是一个特殊的线性规划的问题。

3.3 增广链