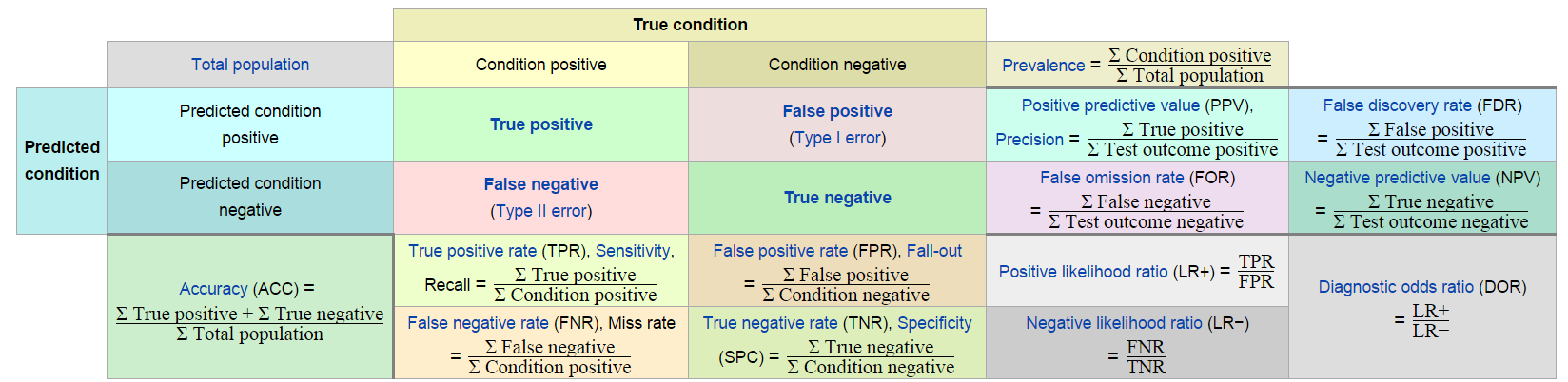
混淆矩阵 Confusion Matrix
简单点的表:
| Prediction | Number Symbol | |||
|---|---|---|---|---|
| P | N | |||
| Real | P | TP | FN | P |
| N | FP | TN | N |
TP - Ture Positive
FN - False Negtive
FP - False Positive
TN - Ture Negtive
准确率 Accuracy
准确率是指分类正确的样本占总样本个数的比例,即
然而当数据集不平衡时(即,当不同类中的样本数量变化很大时),这个指标并不可靠。详情请参考《百面机器学习》2-1。
F1 score
精确率 Precision
精确率是针对我们预测结果而言的,它表示的是预测为正的样本中有多少是真正的正样本。那么预测为正就有两种可能了,一种就是把正类预测为正类(TP),另一种就是把负类预测为正类(FP),也就是
即,你认为的正样本,有多少猜对了(猜的准确性如何)
召回率 Recall
而召回率是针对我们原来的样本而言的,它表示的是样本中的正例有多少被预测正确了。那也有两种可能,一种是把原来的正类预测成正类(TP),另一种就是把原来的正类预测为负类(FN),也就是
如何平衡精确率和召回率
详情请参考《百面机器学习》2-1。
F1 score
精确率是确定分类器中断言为正样本的部分其实际中属于正样本的比例,精度越高则假的正例就越低;召回率则是被分类器正确预测的正样本的比例。两者是一对矛盾的度量,其可以合并成令一个度量,即二者的调和平均值:
如果对于precision和recall的重视不同,则一般的形式:
可以从公式中看到如果 ,则退化成
;如果
,则 recall 有更大影响,反之则 precision 更多影响。
P-R Curve
What is Precision-Recall (PR) curve? https://www.quora.com/What-is-Precision-Recall-PR-curve Precision-recall curves – what are they and how are they used? https://acutecaretesting.org/en/articles/precision-recall-curves-what-are-they-and-how-are-they-used
ROC Curve
What is the difference between a ROC curve and a precision-recall curve? When should I use each? https://www.quora.com/What-is-the-difference-between-a-ROC-curve-and-a-precision-recall-curve-When-should-I-use-each More references related: https://www.zhihu.com/question/30643044 https://zhuanlan.zhihu.com/p/39435695 https://blog.csdn.net/taoyanqi8932/article/details/54409314
Bias-Variance Tradeoff
偏差与方差
Bias refers to the amount of error that is introduced by approximating a real-life problem, which may be extremely complicated, by a simple model. If Bias is high, and/or if the algorithm performs poorly even on your training data, try adding more features, or a more flexible model.
Variance is the amount our model’s prediction would change when using a different training data set. High: Remove features, or obtain more data.
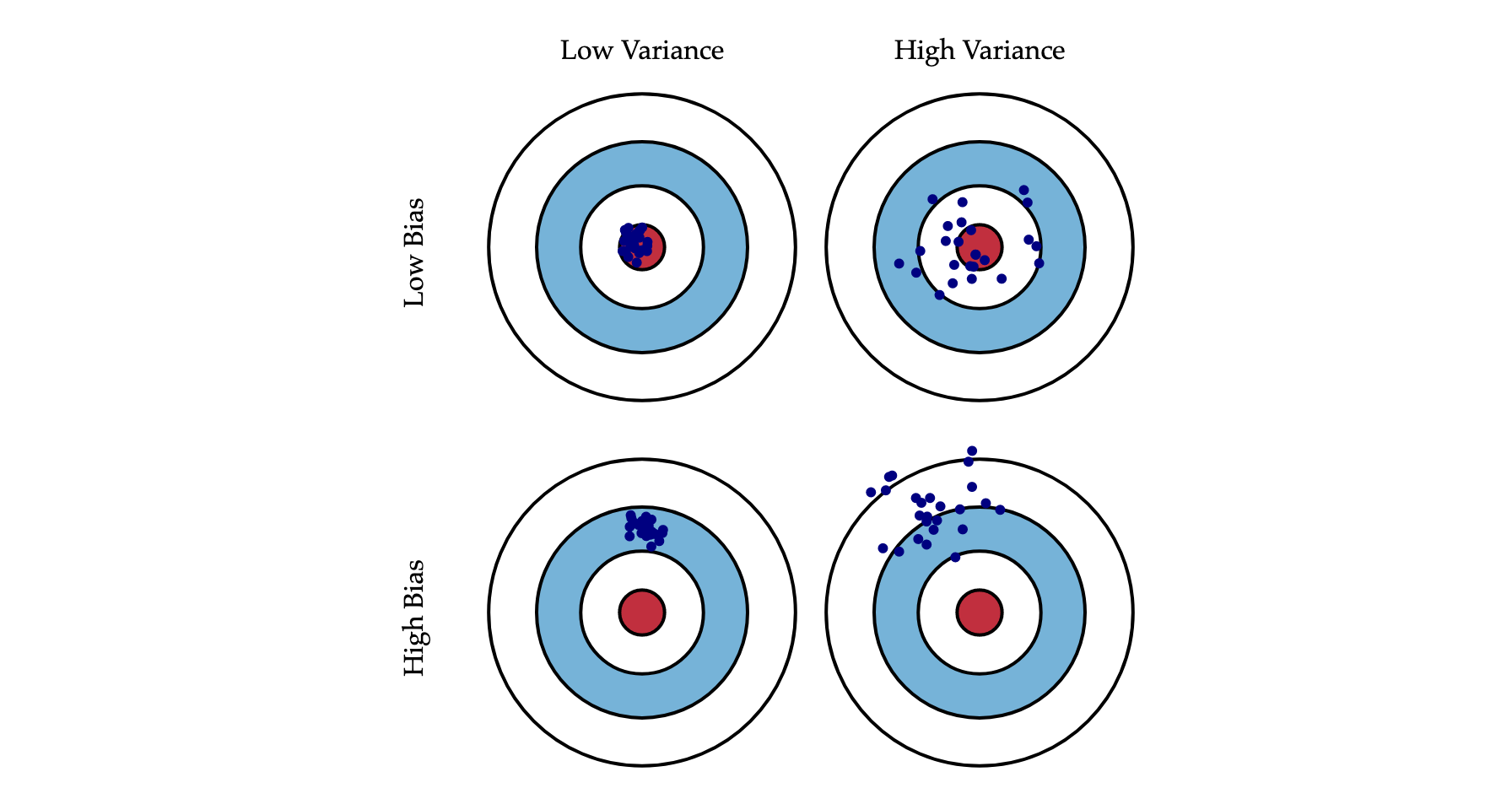
Bias 可以称为准,描述的是根据样本拟合出的模型的输出预测结果的期望与样本真实结果的差距,简单讲,就是在样本上拟合的好不好。要想在bias上表现好,low
bias,就得复杂化模型,增加模型的参数,但这样容易过拟合 (overfitting),过拟合对应上图是high
variance,点很分散。low bias对应就是点都打在靶心附近,所以瞄的是准的,但手不一定稳。
Varience 可以称为确,描述的是样本上训练出来的模型在测试集上的表现,要想在variance上表现好,low varience,就要简化模型,减少模型的参数,但这样容易欠拟合(unfitting),欠拟合对应上图是high bias,点偏离中心。low variance对应就是点都打的很集中,但不一定是靶心附近,手很稳,但是瞄的不准。
在林轩田的课中,对bias和variance还有这样一种解释,我试着不用数学公式抽象的简单概括一下:我们训练一个模型的最终目的,是为了让这个模型在测试数据上拟合效果好,也就是Error(test)比较小,但在实际问题中,test data我们是拿不到的,也根本不知道test data的内在规律(如果知道了,还machine learning个啥 ),所以:
通过什么策略来减小测试集的 Error?
- 让Error(train)尽可能小
- 让Error(train)尽可能等于Error(test)
三段论,因为A小,而且A=B,这样B就小。
那么怎么让Error(train)尽可能小呢?——》把模型复杂化,把参数搞得多多的,这个好理解,十元线性回归,肯定error要比二元线性回归低啊。——》low bias
然后怎么让Error(train)尽可能等于Error(test)呢?——》把模型简单化,把参数搞得少少的。什么叫Error(train)=Error(test)?就是模型没有偏见,对train
test一视同仁。那么怎样的模型更容易有这这种一视同仁的特性,换句话说,更有『通用性』,对局部数据不敏感?那就是简单的模型。——》low
variance
Reference
[1] Understanding the Bias-Variance Tradeoff [2] 机器学习中的Bias(偏差),Error(误差),和Variance(方差)有什么区别和联系
Goodness of Fit
拟合优度(Goodness of Fit)是指回归直线对观测值的拟合程度。度量拟合优度的统计量是可决系数(亦称确定系数)R²。R²最大值为1。R²的值越接近1,说明回归直线对观测值的拟合程度越好;反之,R²的值越小,说明回归直线对观测值的拟合程度越差。
具体可参考《计量经济学》笔记。
Mean Squared Error
综述
In statistics, the mean squared error (MSE) or mean squared deviation (MSD) of an estimator (of a procedure for estimating an unobserved quantity) measures the average of the squares of the errors)—that is, the average squared difference between the estimated values and the actual value. MSE is a risk function, corresponding to the expected value of the squared error loss. The fact that MSE is almost always strictly positive (and not zero) is because of randomness or because the estimator does not account for information that could produce a more accurate estimate.[1]
The MSE is a measure of the quality of an estimator—it is always non-negative, and values closer to zero are better.
The MSE is the second moment) (about the origin) of the error, and thus incorporates both the variance of the estimator (how widely spread the estimates are from one data sample to another) and its bias (how far off the average estimated value is from the truth). For an unbiased estimator,
the MSE is the variance of the estimator. Like the variance, MSE has
the same units of measurement as the square of the quantity being
estimated. In an analogy to standard deviation, taking the square root of MSE yields the root-mean-square error or root-mean-square deviation
(RMSE or RMSD), which has the same units as the quantity being
estimated; for an unbiased estimator, the RMSE is the square root of the
variance, known as the standard error.
公式
The MSE assesses the quality of a predictor (i.e., a function mapping arbitrary inputs to a sample of values of some random variable), or an estimator (i.e., a mathematical function mapping a sample) of data to an estimate of a parameter of the population from which the data is sampled). The definition of an MSE differs according to whether one is describing a predictor or an estimator.
Predictor
If a vector of predictions generated from a sample of n data points on all variables, and
 is the vector of observed values of the variable being predicted, then the within-sample MSE of the predictor is computed as
Estimator
The MSE of an estimator
with respect to an unknown parameter is defined as
This definition depends on the unknown parameter, but the MSE is a priori a property of an estimator. The MSE could be a function of unknown parameters, in which case any estimator of the MSE based on estimates of these parameters would be a function of the data and thus a random variable. If the estimator
 is derived from a sample statistic and is used to estimate some
population statistic, then the expectation is with respect to the
sampling distribution of the sample statistic.
The MSE can be written as the sum of the variance of the estimator and the squared bias
of the estimator, providing a useful way to calculate the MSE and
implying that in the case of unbiased estimators, the MSE and variance
are equivalent.
Error Rate
The proportion of mistakes made if we apply out estimate model function the the training observations in a classification setting.
References
已阅读
https://www.zhihu.com/question/30643044/answer/224360465 https://blog.csdn.net/taoyanqi8932/article/details/54409314
待阅读
https://acutecaretesting.org/en/articles/precision-recall-curves-what-are-they-and-how-are-they-used https://zhuanlan.zhihu.com/p/39435695