0 说明

笔记标题：MIT_LA_Lecture1-3

笔记版本：v1.2.1

对于文档的说明：

1. 你可以在我的 Github 仓库中下载本笔记的 Markdwon 源文档，并通过浏览目录进行更方便高效地浏览；也欢迎在知乎文章中进行浏览。
2. 本笔记参考的课程为 MIT Linear Algebra（麻省理工线性代数），本课程在网易公开课、Bilibili 和 youtube 等网站上都有视频资源，读者可以选择合适的平台观看。
3. 本笔记并未完全按照视频课的内容记录，添加了许多自己的理解、资料的补充和顺序的调整。
4. 本系列笔记在不断更新，已经发布的笔记也会偶尔进行内容更新，版本号可以在文件标题或说明的开头查看，你可以通过 Github 的 commit 信息来查看笔记更新内容。
5. 如果你对笔记内容有好的建议，请提出来，笔者在这里表示感谢。

对于内容的说明：

1. 小写字母表示的向量，比如 ，除非在特殊说明的情况下，都表示的是列向量。用 来表示行向量。
2. 部分矩阵中.用来表示元素省略，并不表示元素为 0。
3. 单位矩阵用 表示。

1 方程组的几何解释

二元线性方程组

我们考虑以下二元方程组以及其矩阵形式 ：

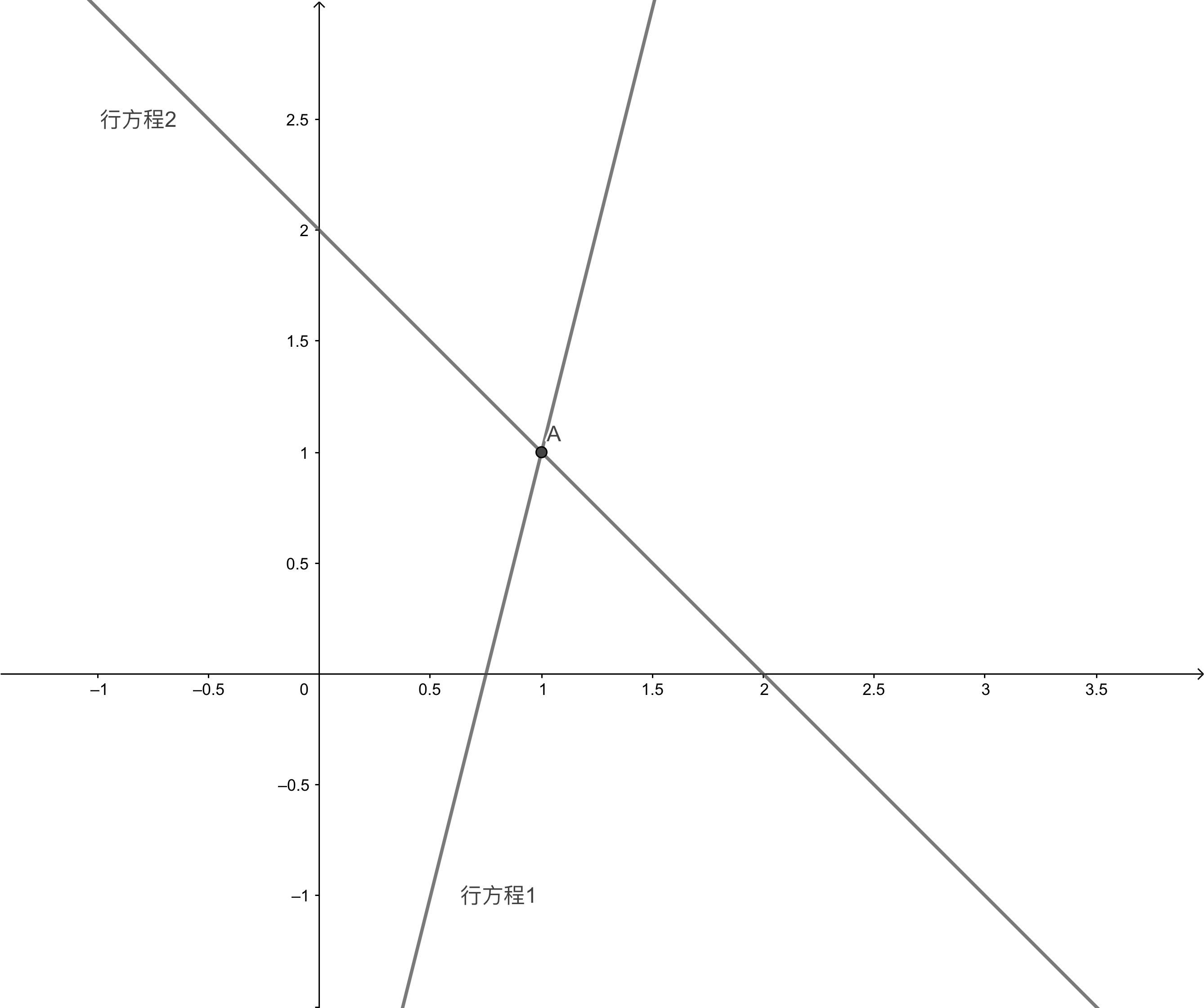
一般我们从每一行来认识这个方程，由于二元方程可以表示在 平面，我们可以画出（1）中两方程所表示的直线，我们也能很容易地求出满足以上方程的组合 %3D(1%2C1)#card=math&code=%28x%2Cy%29%3D%281%2C1%29&height=16&width=79)，即图中的 点。

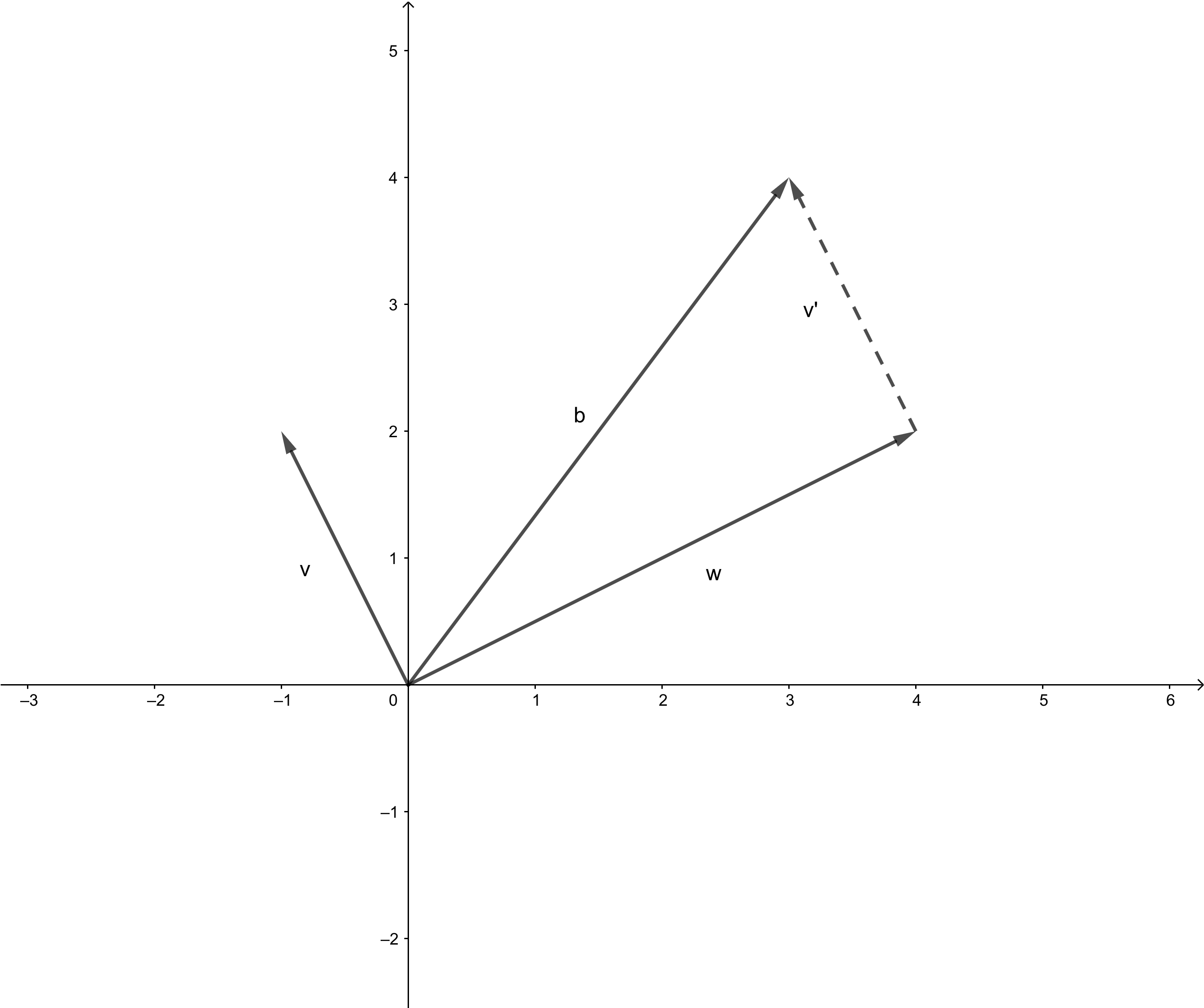
同时，我们也可以从每一列来理解这一方程组，即两向量的何种线性组合可以得到等号右端的向量：

我们也可以在 平面内画出 和 两向量，同理可以找出 ：

多元线性方程组

我们将视角拉回多元情形，比如一般意义上的：

%20%5C%5C%20%5Cvec%20%7B%20x%20%7D%20%3D%7B%20%5Cleft(%20%7B%20x%20%7D%7B%201%20%7D%2C%7B%20x%20%7D%7B%202%20%7D%2C%5Cquad%20…%5Cquad%20%7B%20x%20%7D%7B%20n%20%7D%20%5Cright)%20%20%7D%5E%7B%20T%20%7D%0A%5Ctag%7B3%7D%0A#card=math&code=%7B%20A%20%7D%7B%20m%5Ctimes%20n%20%7D%7B%20%5Cvec%20%7B%20x%20%7D%20%20%7D%7B%20n%5Ctimes%201%20%7D%3D%7B%20%5Cvec%20%7B%20b%20%7D%20%20%7D%7B%20n%5Ctimes%201%20%7D%5C%5C%20A%3D%5Cleft%28%20%7B%20%5Cvec%20%7B%20a%20%7D%20%20%7D%7B%201%20%7D%2C%7B%20%5Cvec%20%7B%20a%20%7D%20%20%7D%7B%202%20%7D%2C%5Cquad%20…%7B%20%5Cquad%20%5Cvec%20%7B%20a%20%7D%20%20%7D%7B%20n%20%7D%20%5Cright%29%20%5C%5C%20%5Cvec%20%7B%20x%20%7D%20%3D%7B%20%5Cleft%28%20%7B%20x%20%7D%7B%201%20%7D%2C%7B%20x%20%7D%7B%202%20%7D%2C%5Cquad%20…%5Cquad%20%7B%20x%20%7D%7B%20n%20%7D%20%5Cright%29%20%20%7D%5E%7B%20T%20%7D%0A%5Ctag%7B3%7D%0A&height=60&width=583)

可以以列向量的线性表示的角度来看，即：

矩阵列的线性组合

于是我们可以将方程组的几何解释理解为，在 维空间中，系数矩阵 的列向量，是否可以通过某组系数来线性表示为 。线性方程组或矩阵方程看成矩阵列的线性组合是理解线性方程组、矩阵方程的很好的方式。

当然，是否存在这样的一组数据也就是等价于这个方程组是否有解，也可以从诸多角度来理解，这里不做过多解释。

2 矩阵消元

主元，行阶梯型，简化行阶梯型

考虑以下线性方程组：

我们可以通过对（6）中方程加减，从而得到一个等价的更容易求解的方程组，而实际中，我们是对其系数矩阵或增广矩阵进行行变换，得到理想的形式，从而方便求解。比如，我们将（5）中的增广矩阵进行如下行变换得到（6）：

主元

我们接下来观察（6）中最后的增广矩阵的系数矩阵部分，其非零行首非零元被称为主元（pivot），比如这里的主元是 1，2 和 5。寻找主元的过程被称为pivoting。随后把主元所在的行（或列）交换到固定位置，用于随后的计算。主元所在的列组成列空间的一个基。但实际的算法很少移动矩阵的行，因为这对于大矩阵（含有几千到几百万的行与列）将招致极大的时间花费；替代的办法是仅仅记录矩阵的行的交换信息。

行阶梯型矩阵

（6）中进行行变换的结果是得到了一个行阶梯形矩阵（Row Echelon Form），它满足以下条件:

• 所有非零行（矩阵的行至少有一个非零元素）在所有全零行的上面。即全零行都在矩阵的底部。
• 非零行的首项系数（leading coefficient），即主元严格地比上面行的首项系数更靠右。
• 首项系数所在列，在该首项系数下面的元素都是零（前两条的推论）。

简化行阶梯形矩阵

按理说找到行阶梯形矩阵就能够对方程组进行求解，同时也找到了系数列向量的基，但我们发现，比如第一行第二个位置不为 0，这种主元列上还有其他非零元素是很讨厌的，比如从第一行我们可以看出，为了求解 ，我们还必须先得到 和 ，为了求解 还必须先求解 。如果每一行最多只有一个主元，那么我们就能更容易地用非主元列来表示出主元列了，为此我们可以进行如下行变换：

这样我们就直接解出了结果，我们将这种化简后的行阶梯形矩阵称为简化行阶梯形矩阵（reduced row echelon form），它需要满足额外的条件：每个首项系数是 1，且是其所在列的唯一的非零元素。我们再举一个例子比如：

两种消元法

高斯消元法

数学上，高斯消元法（Gaussian Elimination），是线性代数中的一个算法，可用来为线性方程组，求出矩阵的秩，以及求出可逆方阵的逆矩阵。当用于一个矩阵时，高斯消元法会产生出一个行阶梯形矩阵。

也就是（6）中的实现过程，就是高斯消元的过程。

高斯-若当消元法

高斯－若尔当消元法（Gauss-Jordan Elimination），是高斯消元法的另一个版本。它在线性代数中用来找出线性方程组的解，其方法与高斯消元法相同。唯一相异之处就是这算法产生出来的矩阵是一个简化行梯阵式，而不是高斯消元法中的行梯阵式。

相比起高斯消元法，此算法的效率比较低，却可把方程组的解用矩阵一次过表示出来。

矩阵行的线性组合

在 1 中，我们将矩阵乘列向量理解为矩阵的列向量以列向量为系数进行线性表示，即矩阵列的线性组合(a combination of the columns of the matrix)。那么，如何理解矩阵的行表示呢？也就是如何来表示行变换呢：

也就是说，我们可以将行向量 × 矩阵理解为矩阵的行向量以行向量为系数进行线性表示，即矩阵行的线性组合，最终得到一个 4 维行向量。那么更进一步地理解，多个行向量 × 矩阵也就可以表示如下，最终得到一个 3×4 的矩阵，即 3 个 4 维行向量：

矩阵的初等变换

有了矩阵行表示之后，我们就可以很容易地理解（6）总矩阵的行变换，通过对矩阵左乘（右乘）可逆方阵来实现矩阵的行列变换，这就是矩阵的初等变换。

初等行变换

左乘初等矩阵可以实现矩阵的行变换。比如，我们是通过第 2 行 - 3 倍的第 1 行得（6）中间的矩阵，用矩阵变换也就是：

在此基础上，我们是通过第 3 行 - 2 倍的第2行得到（6）右边的矩阵，用矩阵变换也就是：

（10）也可以表示为 %20%3DU#card=math&code=%7B%20E%20%7D%7B%2032%20%7D%5Cleft%28%20%7B%20E%20%7D%7B%2021%20%7DA%20%5Cright%29%20%3DU&height=16&width=93)，虽然矩阵的顺序不能变，但矩阵计算具有结合律(associate law)，所以也可以写成%20A%3DU#card=math&code=%5Cleft%28%20%7B%20E%20%7D%7B%2032%20%7D%7B%20E%20%7D%7B%2021%20%7D%20%5Cright%29%20A%3DU&height=16&width=93)，即A可以通过某种行变换一次性变为 。

初等列变换

右乘初等矩阵，也就是1中我们理解的那样，我们便可以实现矩阵的列变换。比如我们想交换两列的顺序：

3 矩阵乘法和逆

矩阵乘法的解释

我们考虑以下情况的矩阵乘法结果中的某一项 ：

我们有以下几种理解矩阵乘法的方式。

代数表达式

即 矩阵的第 3 行与 B 矩阵的第 4 列的点积：

%20%5Ccdot%20%5Cleft(%20col4%5Cquad%20of%5Cquad%20B%20%5Cright)%20%3D%7B%20a%20%7D%7B%2031%20%7D%7B%20b%20%7D%7B%2014%20%7D%2B%7B%20a%20%7D%7B%2032%20%7D%7B%20b%20%7D%7B%2024%20%7D%2B…%3D%5Csum%20%7B%20k%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20a%20%7D%7B%203k%20%7D%7B%20b%20%7D%7B%20k4%20%7D%20%7D%0A%5Ctag%7B15%7D%0A#card=math&code=%7B%20c%20%7D%7B%2034%20%7D%3D%5Cleft%28%20row3%5Cquad%20of%5Cquad%20A%20%5Cright%29%20%5Ccdot%20%5Cleft%28%20col4%5Cquad%20of%5Cquad%20B%20%5Cright%29%20%3D%7B%20a%20%7D%7B%2031%20%7D%7B%20b%20%7D%7B%2014%20%7D%2B%7B%20a%20%7D%7B%2032%20%7D%7B%20b%20%7D%7B%2024%20%7D%2B…%3D%5Csum%20%7B%20k%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20a%20%7D%7B%203k%20%7D%7B%20b%20%7D_%7B%20k4%20%7D%20%7D%0A%5Ctag%7B15%7D%0A&height=40&width=583)

A列向量的线性组合

在了解了初等变换后，我们可以将 这个等式看做，矩阵 的各列向量通过乘 的各列来得到 的各列，即 的各列是矩阵 各列的线性组合。

Columns of C are the combinations of columns of A.

B行向量的线性组合

我们还可以将 这个等式看做，矩阵 的各行向量通过乘 的各行来得到 的各行，即 的各行是矩阵B的各行的线性组合。

Rows of C are the combinations of rows of B.

A的列×B的行

以上有两种理解方法，即左边这个列向量分别乘 1 和 6 得到右边这两个列向量，或右边这个行向量分别乘2，3，4得到右边 3 个行向量。而 其实就是 和 分别以 进行列划分和行划分后， 的列和 的行的乘积的和：

分块矩阵

有时候，我们也可以通过对矩阵分块，得到一些为 0 矩阵或单位矩阵的项，使计算变得更加容易。以下给出了矩阵分块的一种划分，当然矩阵分块不一定局限于这种格式：

逆矩阵

对于方阵 ，如果有 ，则称A是可逆矩阵（invertible）或非奇异矩阵（non-sigular），反之则称方阵 为不可逆矩阵或奇异矩阵。

如何理解或判定矩阵是否可逆

行列式是否为0

如果 ，则 不可逆，反之可逆。

秩是否为n

如果 %20%3Dn#card=math&code=rank%5Cleft%28%20A%20%5Cright%29%20%3Dn&height=16&width=78)，则 可逆，否则 不可逆。

列向量是否线性相关

以列向量分析，在 维空间内，如果列向量线性相关，即线性无关的列向量个数小于 ，比如是 ，那么由这 个列向量表示出的向量一定在 维平面内，而等式右端的 各列共有 维向量，所以I无法由这些列向量线性表出，即不存在与 相乘积为 的矩阵。

Ax=0

如果能找到一个非零向量 ，使得 成立，则A不可逆。因为如果 存在，将其左乘于等式，便能得到 ，这与非零向量的假设矛盾了。

求逆矩阵

高斯-若当消元

求逆矩阵的本质是同时对 个方程组进行高斯消元或进行初等变换。我们可以通过对其增广矩阵进行行变换，使 变为 ，与此同时原本的 就变成了 ，其原理如下：