随机试验
随机试验是概率论的一个基本概念。 概括地讲,在概率论中把符合下面三个特点的试验叫做随机试验:
- 可以在相同的条件下重复的进行。
- 每次试验的可能结果不止一个,并且能事先明确试验的所有可能结果。
- 进行一次试验之前不能确定哪一个结果会出现。
随机试验通常用 (event)表示:
:抛1颗骰子,观察出现的点数情况。
样本空间
随机试验 的所有可能结果组成的集合成为
的样本空间,记为
。
样本空间的元素,即E的每个结果,成为样本点。
= {点1, 点2, 点3, 点4, 点5, 点6}
点 1 到点 6 均为样本点。
随机事件
随机试验 的样本空间
的子集为
的随机事件,在每次试验中,当且仅当这一子集中的一个样本点出现时,称这一事件发生。由一个样本点组成的单点集,成为基本事件。
本身成为必然事件。
不包含任何样本点,成为不可能事件。
:抛 1 颗骰子,出现的点数大于 3。
随机变量
设随机试验的样本空间为 ,
#card=math&code=X%3DX%5Cleft%28%20e%20%5Cright%29&height=20&width=74) 是定义在样本空间上的实值单值函数,则称
为随机变量。一般以大写字母
等表示随机变量,而以小写字母
等表示实数。随机变量的取值随试验的结果而定,在试验之前不能预知取值,且它的取值有一定的概率。
随机变量有离散型和连续型:
离散型随机变量有其分布律;
连续型随机变量可以满足一定分布。
为点数对应的数字:
,离散型
%20%3D%5Cfrac%20%7B%201%20%7D%7B%202%20%7D#card=math&code=P%5Cleft%28%20X%3E3%20%5Cright%29%20%3D%5Cfrac%20%7B%201%20%7D%7B%202%20%7D&height=37&width=111)
离散型随机变量分布律
0-1分布
伯努利分布(英语:Bernoulli distribution, 又名两点分布或者0-1分布, 是一个离散型概率分布, 为纪念瑞士科学家雅各布·伯努利而命名). 若伯努利试验成功, 则伯努利随机变量取值为1. 若伯努利试验失败, 则伯努利随机变量取值为0. 记其成功概率为, 失败概率为
.
- 其概率密度函数为:
其期望值为:

其方差为:

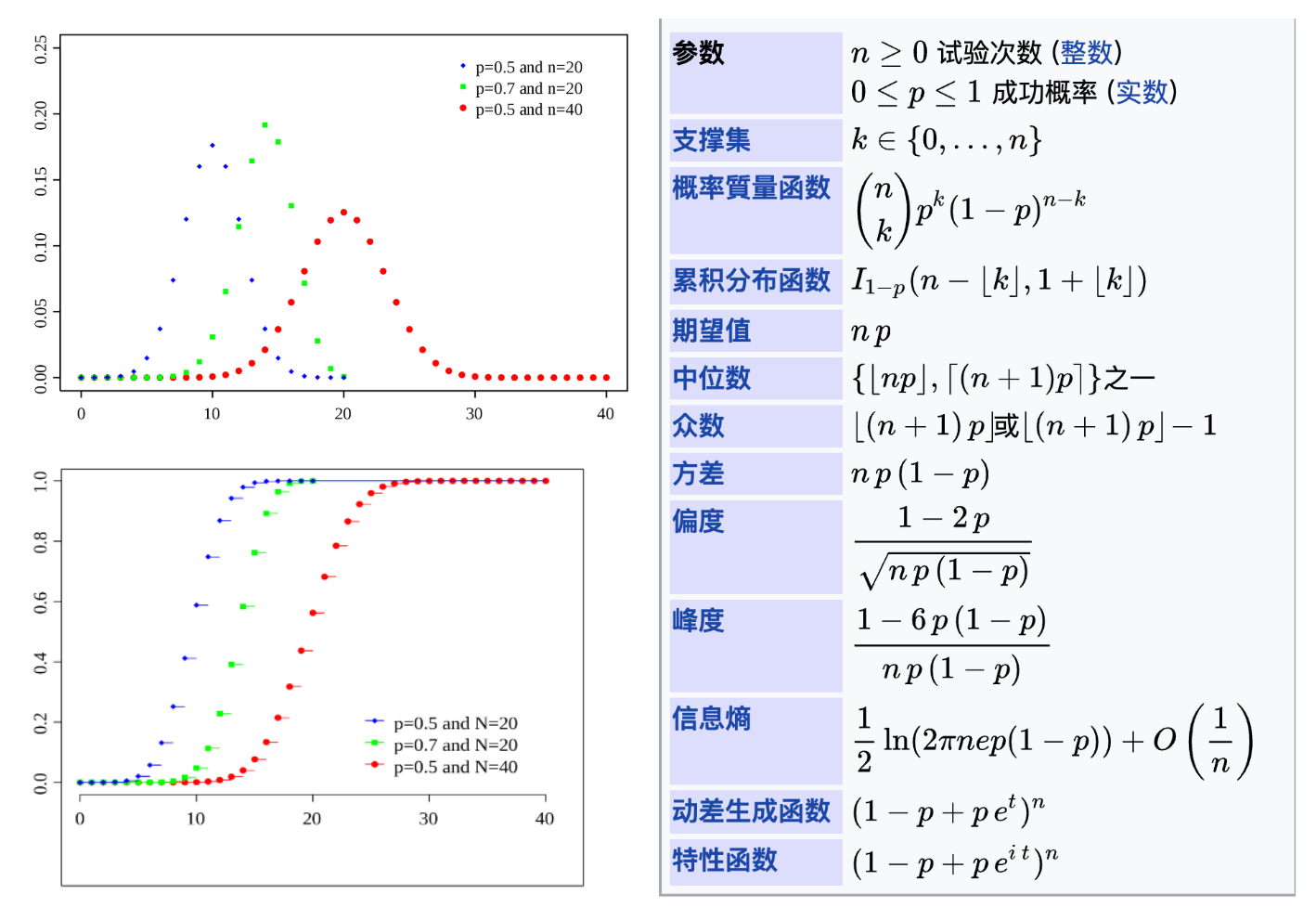
二项分布
在概率论和统计学中, 二项分布 (英语:Binomial distribution)是n个独立的是/非试验中成功的次数的离散概率分布,其中每次试验的成功概率为p。这样的单次成功/失败试验又称为伯努利试验。实际上,当n = 1时,二项分布就是伯努利分布。二项分布是显著性差异的二项试验的基础。
几何分布
在概率论和统计学中,几何分布(英语:Geometric distribution)指的是以下两种离散型概率分布中的一种:
在伯努利试验中,得到一次成功所需要的试验次数 X。X的值域是{ 1, 2, 3, … }
在得到第一次成功之前所经历的失败次数Y = X − 1。Y的值域是{ 0, 1, 2, 3, … }
实际使用中指的是哪一个取决于惯例和使用方便。
这两种分布不应该混淆。前一种形式(X的分布)经常被称作shifted geometric distribution;但是,为了避免歧义,最好明确地说明取值范围。
如果每次试验的成功概率是p,那么k次试验中,第k次才得到成功的概率是,
其中 k = 1, 2, 3, ….
上式描述的是取得一次成功所需要的试验次数。而另一种形式,也就是第一次成功之前所失败的次数,可以写为,
其中k = 0, 1, 2, 3, ….
两种情况产生的序列都是几何数列。
比如,假设不停地掷骰子,直到得到1。投掷次数是随机分布的,取值范围是无穷集合{ 1, 2, 3, … },并且是一个p = 1/6的几何分布。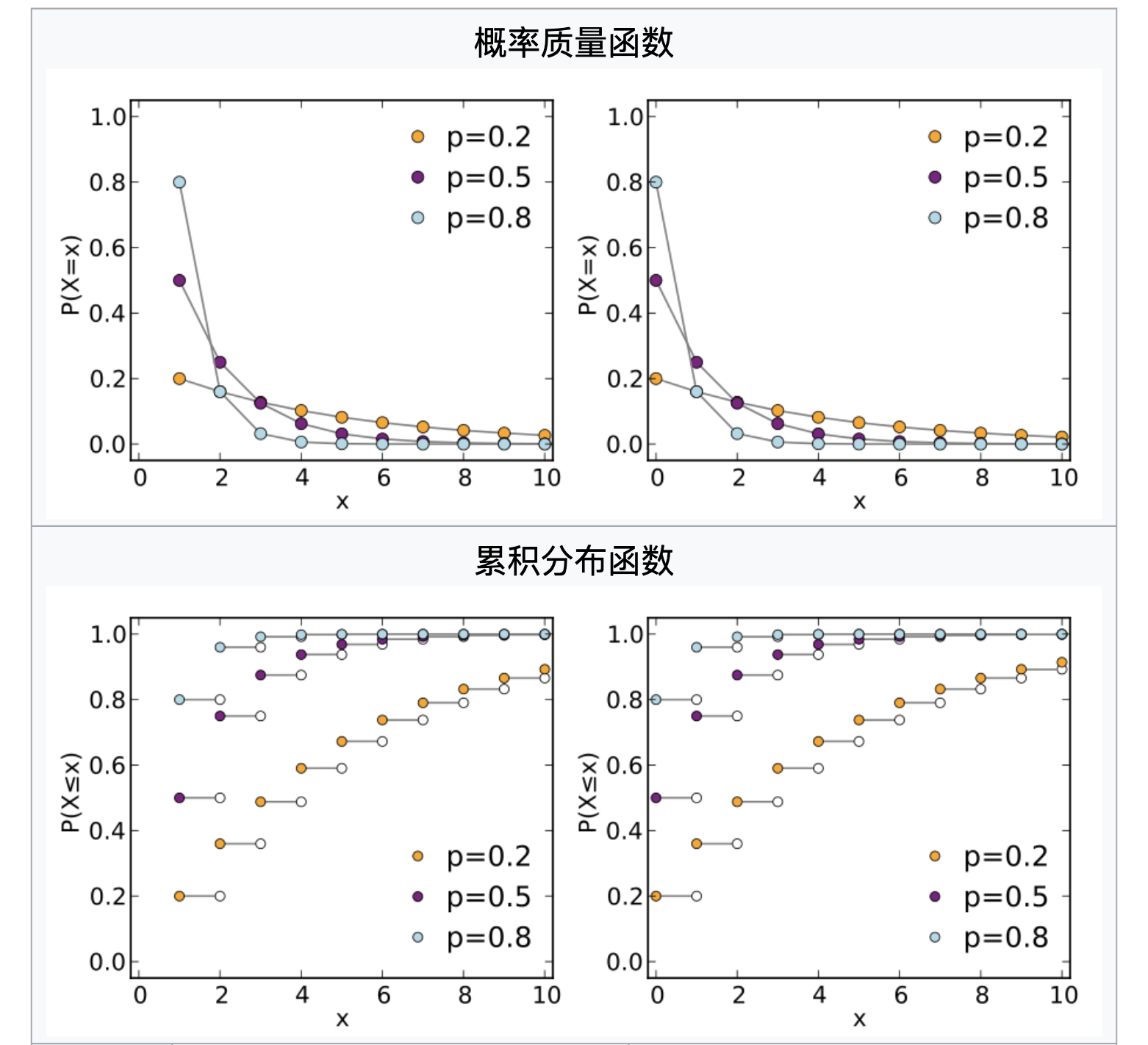
超几何分布
超几何分布是统计学上一种离散概率分布。它描述了由有限个物件中抽出 n 个物件,成功抽出指定种类的物件的个数(不归还 (without replacement))。
例如在有 N 个样本,其中 K 个是不及格的。超几何分布描述了在该 N 个样本中抽出 n 个,其中 k 个是不及格的几率:
上式可如此理解: 表示所有在 N 个样本中抽出 n 个的方法数目。
表示在 K 个样本中,抽出 k 个的方法数目,即组合数,又称二项式系数。剩下来的样本都是及格的,而及格的样本有
个,剩下的抽法便有
种。
若 n=1,超几何分布还原为伯努利分布。
记号
**
若随机变量 X 服从参数为 的超几何分布,则记为
。
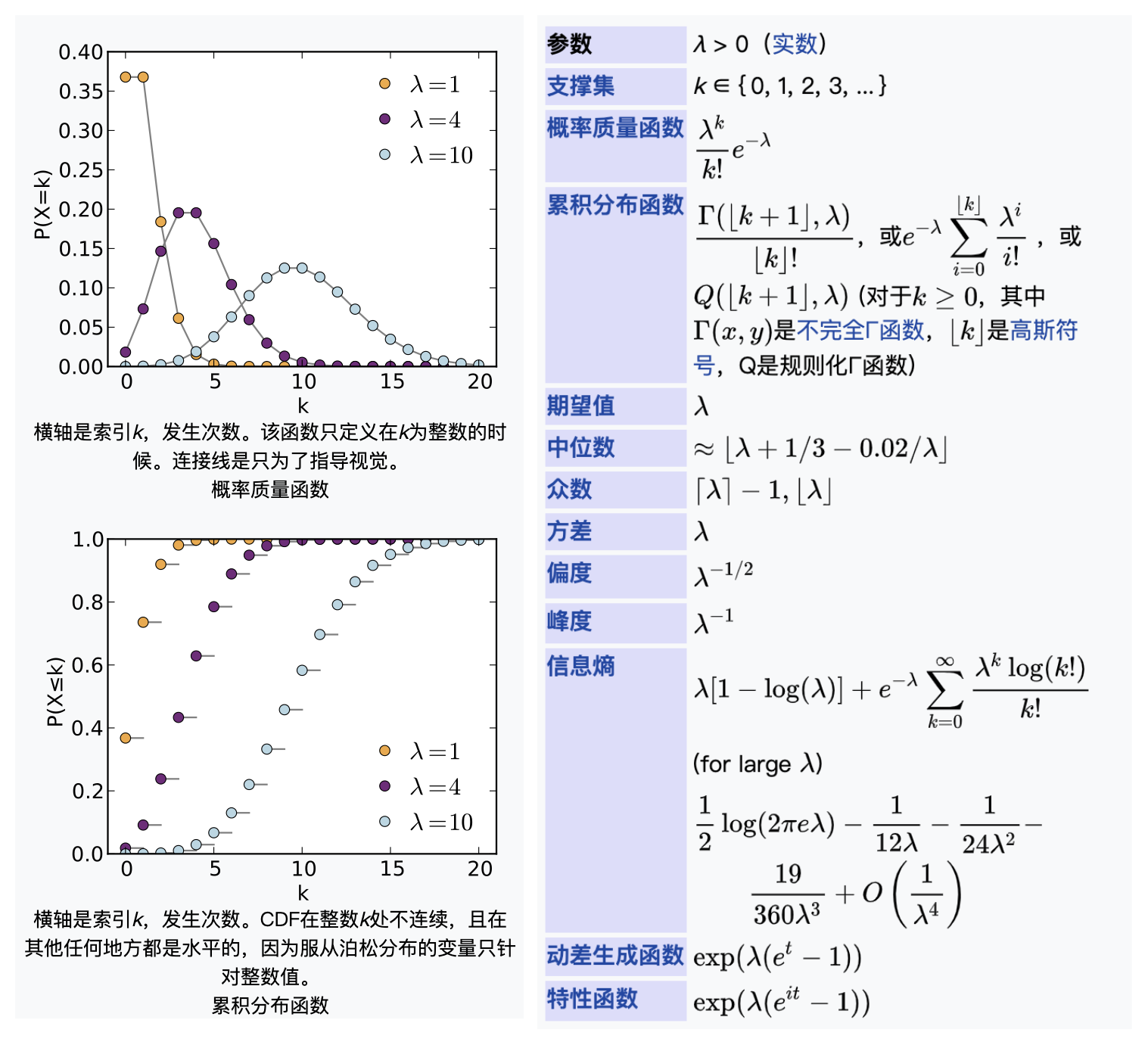
泊松分布
泊松分布(法语:loi de Poisson,英语:Poisson distribution)又称帕松分布、普阿松分布、布瓦松分布、布阿松分布、波以松分布、卜氏分配、泊松小数法则(Poisson law of small numbers),是一种统计与概率学里常见到的离散概率分布,由法国数学家西莫恩·德尼·泊松在1838年时发表。
泊松分布适合于描述单位时间内随机事件发生的次数的概率分布。如某一服务设施在一定时间内受到的服务请求的次数,电话交换机接到呼叫的次数、汽车站台的候客人数、机器出现的故障数、自然灾害发生的次数、DNA序列的变异数、放射性原子核的衰变数、激光的光子数分布等等。
泊松分布的概率质量函数为:
泊松分布的参数λ是单位时间(或单位面积)内随机事件的平均发生率。
连续型随机变量的分布
分布函数、概率密度函数、随机变量的函数的分布
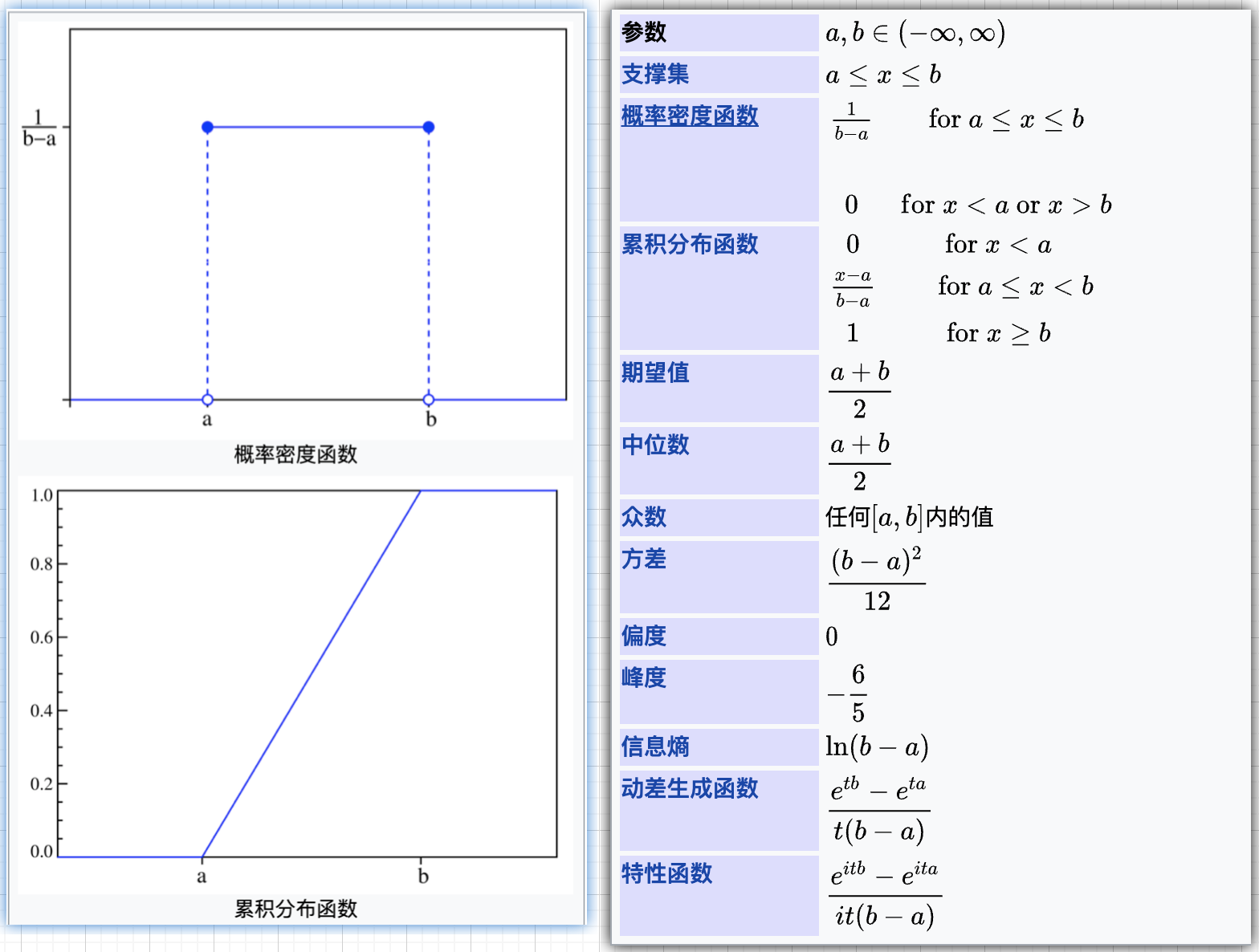
均匀分布
连续型均匀分布,如果连续型随机变量 具有如下的概率密度函数,则称
服从
上的均匀分布(uniform distribution),记作
一个均匀分布在区间 [a,b] 上的连续型随机变量 可给出如下函数:
概率密度函数:
累积分布函数:
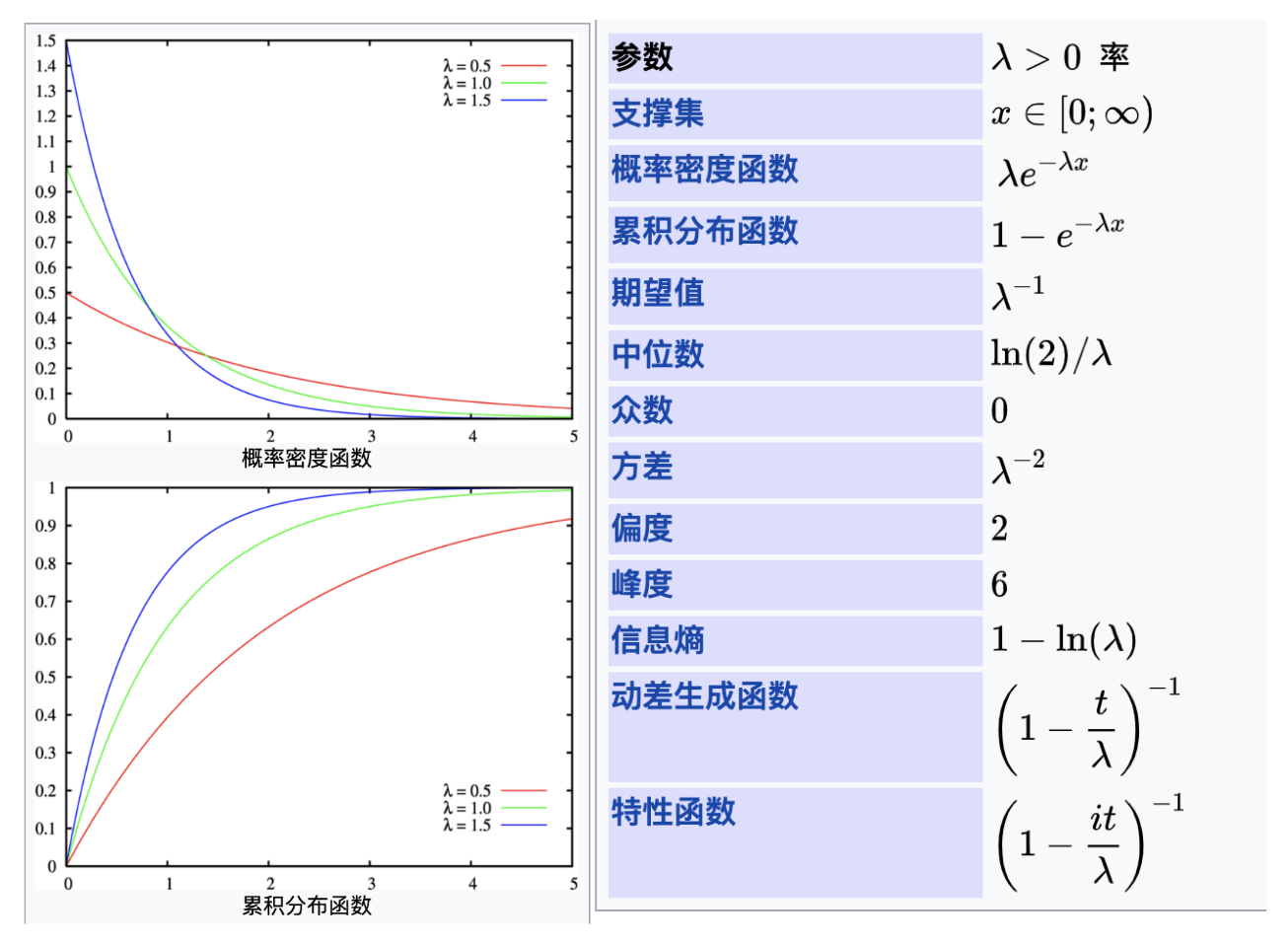
指数分布
在概率论和统计学中,指数分布(英语:Exponential distribution)是一种连续概率分布。指数分布可以用来表示独立随机事件发生的时间间隔,比如旅客进入机场的时间间隔、打进客服中心电话的时间间隔、中文维基百科新条目出现的时间间隔等等。
概率密度函数
一个指数分布的概率密度函数是:
其中λ > 0是分布的一个参数,常被称为率参数(rate parameter)。即每单位时间发生该事件的次数。指数分布的区间是[0,∞)。 如果一个随机变量X 呈指数分布,则可以写作:X ~ Exponential(λ)。
累积分布函数
累积分布函数可以写成:
正态分布
正态分布(台湾作常态分布,英语:normal distribution)又名高斯分布(英语:Gaussian distribution),是一个非常常见的连续概率分布。正态分布在统计学上十分重要,经常用在自然和社会科学来代表一个不明的随机变量。[1][2]
若随机变量 X 服从一个位置参数为 、尺度参数为
的正态分布,记为:
则其概率密度函数为:
正态分布的数学期望值或期望值 等于位置参数,决定了分布的位置;其方差
的开平方或标准差
正态分布的概率密度函数曲线呈钟形,因此人们又经常称之为钟形曲线(类似于寺庙里的大钟,因此得名)。我们通常所说的标准正态分布是位置参数 ,尺度参数
的正态分布(见下图中红色曲线).