单因素试验的方差分析

背景

首先来说说我们为什么要用单因素方差分析（one-way ANOVA)。在做一些实验时，我们通常会把样本分成不同的组，给予不同的对待。例如，我们想研究某种药物在不同剂量下对人们的作用。我们可能会将病人随机分为同等大小的三组，A 组每天吃一片，B 组每天吃两片，C 组每天吃三片。因为我们只研究这个药品计量对病人的影响，所以是单因素分析，如果想要加入别的因素，例如，年龄，就需要用到多因素分析了。在上述实验中，我们给了三种不同的计量，所以这个药物计量因素下有三个水平（level）。实验结束以后，你老板问你，这三组病人的表现有显著的区别吗？这个时候，你就可以使用 ANOVA 来回答你老板的问题啦。

虽然 ANOVA 叫做方差分析，但是他的目的是检验每个组的平均数是否相同（敲黑板！）。也就是说，ANOVA 的零假设（null hypothesis）是 方差分析 - 图1。现在，我们换一个角度考虑这个问题，如果这三组病人的表现并没有显著的区别，那他们其实是同一个总体的三次随机抽样。反过来说，我们想要分析，是不是有一组病人他们的表现非常与众不同，让这组病人不是来自同一个总体。

为什么是方差分析？

为什么不直接比较均值？

举个例子，方差分析 - 图2 组：29，30，31；方差分析 - 图3组：3，31，41。方差分析 - 图4 组均值为30，方差分析 - 图5 组均值 25，看起来 方差分析 - 图6 组大一些，但实际上 方差分析 - 图7 组有两个值都大于 方差分析 - 图8 组。

这是因为，不同组极端值可能会影响到均值，从而给判断造成误导。

为什么不用 t 检验？

我们有一个样本后进行一次 t 检验，在这里，每一组就相当于一个样本，那么比如有三组， 方差分析 - 图9 就要做 3 次独立的 方差分析 - 图10 检验。但是 方差分析 - 图11 检验是每次给定一个显著性水平，比如我们给定 方差分析 - 图12，也就是每次犯错的概率为 0.05，那么每次不犯错的概率是 0.95，三次不犯错的概率为 方差分析 - 图13，那么我们犯错的概率就高达 0.142625。

而方差分析是一次检验，犯错的概率就小很多，但方差分析也有局限性，它只能检验各组之间的均值是否有差异，并不能给出谁大谁小，所以，适当时候有必要方差分析后，再进行 方差分析 - 图14 检验。

前提假设

在具体说如何理解 ANOVA 之前，我们先来说 ANOVA 有哪些假设。如果你的实验不能满足 ANOVA 的假设，那你需要考虑别的分析方法或者改变实验设计。ANOVA 有主要有以下 3 个假设：

  1. 方差的同质性（homogeneity of variance）。可以理解为每组样本背后的总体（也叫族群）都有相同的方差；
  2. 族群遵循正态分布；
  3. 每一次抽样都是独立的。在我们的例子中，每一个病人只能提供一个数据。对于一些实验一个样本需要提供多个数据，有其他相应的 ANOVA 分析方法。

原假设

方差分析 - 图15

方差分析 - 图16 不全相等

平方和的分解

假设我们得到的抽样结果是这样的：

方差分析 - 图17

方差分析 - 图18

现在，我们终于可以来看方差分析。首先我们来看单因素试验方差分析表：

方差来源 平方和 自由度 均方 F比
因素 A 方差分析 - 图19 s-1 方差分析 - 图20 方差分析 - 图21
误差 方差分析 - 图22 n-s 方差分析 - 图23
总和 方差分析 - 图24 n-1(即总样本方差自由度)

总偏差平方和：方差分析 - 图25%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D#card=math&code=%7B%20S%20%7D%7B%20T%20%7D%3D%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20s%20%7D%7B%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20%7B%20n%20%7D%7B%20j%20%7D%20%7D%7B%20%7B%20%5Cleft%28%20%7B%20%7B%20X%20%7D_%7B%20ij%20%7D%20%7D-%5Cbar%20%7B%20X%20%7D%20%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D&height=55&width=179)

我们可以将其分解：方差分析 - 图26%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%20%5C%5C%20%3D%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20s%20%7D%7B%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20%7B%20n%20%7D%7B%20j%20%7D%20%7D%7B%20%7B%20%5Cleft%5B%20%5Cleft(%20%7B%20%7B%20X%20%7D%7B%20ij%20%7D%20%7D-%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%7B%20%5Cbullet%20j%20%7D%20%5Cright)%20%2B%5Cleft(%20%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%7B%20%5Cbullet%20j%20%7D-%5Cbar%20%7B%20X%20%7D%20%20%5Cright)%20%20%5Cright%5D%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%20%5C%5C%20%3D%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20s%20%7D%7B%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20%7B%20n%20%7D%7B%20j%20%7D%20%7D%7B%20%7B%20%5Cleft(%20%7B%20%7B%20X%20%7D%7B%20ij%20%7D%20%7D-%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%7B%20%5Cbullet%20j%20%7D%20%5Cright)%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%20%2B%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20s%20%7D%7B%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20%7B%20n%20%7D%7B%20j%20%7D%20%7D%7B%20%7B%20%5Cleft(%20%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%7B%20%5Cbullet%20j%20%7D-%5Cbar%20%7B%20X%20%7D%20%20%5Cright)%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%20%5C%5C%20%3D%7B%20S%20%7D%7B%20E%20%7D%2B%7B%20S%20%7D%7B%20A%20%7D#card=math&code=%7B%20S%20%7D%7B%20T%20%7D%3D%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20s%20%7D%7B%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20%7B%20n%20%7D%7B%20j%20%7D%20%7D%7B%20%7B%20%5Cleft%28%20%7B%20%7B%20X%20%7D%7B%20ij%20%7D%20%7D-%5Cbar%20%7B%20X%20%7D%20%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%20%5C%5C%20%3D%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20s%20%7D%7B%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20%7B%20n%20%7D%7B%20j%20%7D%20%7D%7B%20%7B%20%5Cleft%5B%20%5Cleft%28%20%7B%20%7B%20X%20%7D%7B%20ij%20%7D%20%7D-%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%7B%20%5Cbullet%20j%20%7D%20%5Cright%29%20%2B%5Cleft%28%20%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%7B%20%5Cbullet%20j%20%7D-%5Cbar%20%7B%20X%20%7D%20%20%5Cright%29%20%20%5Cright%5D%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%20%5C%5C%20%3D%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20s%20%7D%7B%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20%7B%20n%20%7D%7B%20j%20%7D%20%7D%7B%20%7B%20%5Cleft%28%20%7B%20%7B%20X%20%7D%7B%20ij%20%7D%20%7D-%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%7B%20%5Cbullet%20j%20%7D%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%20%2B%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20s%20%7D%7B%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20%7B%20n%20%7D%7B%20j%20%7D%20%7D%7B%20%7B%20%5Cleft%28%20%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%7B%20%5Cbullet%20j%20%7D-%5Cbar%20%7B%20X%20%7D%20%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%20%5C%5C%20%3D%7B%20S%20%7D%7B%20E%20%7D%2B%7B%20S%20%7D_%7B%20A%20%7D&height=195&width=724)

方差分析 - 图27：误差平方和

方差分析 - 图28：效应平方和

自由度

方差分析 - 图29：比较简单的理解方法是，每组（即每个 方差分析 - 图30 ）是 方差分析 - 图31 个组一共 n-s；

方差分析 - 图32：比较简单的理解方法是，将每组数据的均值看成一个数据，共 方差分析 - 图33 个，求这 方差分析 - 图34 个数据的方差，方差自由度为 s-1 （实际需要严谨的证明）；

分布与期望

方差分析 - 图35

由于 方差分析 - 图36%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%20%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft(%20%7B%20n%20%7D%7B%20j%20%7D-1%20%5Cright)#card=math&code=%5Cfrac%20%7B%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20%7B%20n%20%7D%7B%201%20%7D%20%7D%7B%20%7B%20%5Cleft%28%20%7B%20X%20%7D%7B%20ij%20%7D-%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%7B%20%5Cbullet%20j%20%7D%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%20%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft%28%20%7B%20n%20%7D%7B%20j%20%7D-1%20%5Cright%29&height=49&width=244)，且各 方差分析 - 图37 相互独立，由卡方分布可加性知 方差分析 - 图38#card=math&code=%5Cfrac%20%7B%20%7B%20S%20%7D_%7B%20E%20%7D%20%7D%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%20%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft%28%20%7B%20n%20%7D-s%20%5Cright%29&height=41&width=122) ，这也再次说明误差平方和的自由度为 n-s 。

故 方差分析 - 图39%20%3D%5Cleft(%20n-s%20%5Cright)%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D#card=math&code=E%5Cleft%28%20%7B%20S%20%7D_%7B%20E%20%7D%20%5Cright%29%20%3D%5Cleft%28%20n-s%20%5Cright%29%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D&height=23&width=144)

方差分析 - 图40

可以推出（过程略）方差分析 - 图41%20%3D%5Cleft(%20s-1%20%5Cright)%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%2B%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20s%20%7D%7B%20%7B%20n%20%7D%7B%20j%20%7D%7B%20%5Cdelta%20%20%7D%7B%20j%20%7D%5E%7B%202%20%7D%20%7D#card=math&code=E%5Cleft%28%20%7B%20S%20%7D%7B%20A%20%7D%20%5Cright%29%20%3D%5Cleft%28%20s-1%20%5Cright%29%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%2B%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20s%20%7D%7B%20%7B%20n%20%7D%7B%20j%20%7D%7B%20%5Cdelta%20%20%7D%7B%20j%20%7D%5E%7B%202%20%7D%20%7D&height=52&width=222)，其中 ${ \delta }{ j }={ \mu }_{ j }-\mu $。

进一步还有：

  1. 方差分析 - 图42 与 方差分析 - 图43 独立；
  2. 当 方差分析 - 图44 为真时，方差分析 - 图45#card=math&code=%5Cfrac%20%7B%20%7B%20S%20%7D_%7B%20A%20%7D%20%7D%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%20%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft%28%20s-1%20%5Cright%29&height=41&width=120) 。

拒绝域

从上一小节分布和期望，我们可以总结以下几点：

  1. 方差分析 - 图46 与 方差分析 - 图47 独立；
  2. 方差分析 - 图48#card=math&code=%5Cfrac%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%20%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft%28%20%7B%20n%20%7D-s%20%5Cright%29&height=41&width=122)，因此无论 方差分析 - 图49 是否为真， ![](https://g.yuque.com/gr/latex?E%5Cleft(%20%7B%20S%20%7D%7B%20E%20%7D%20%5Cright)%20%3D%5Cleft(%20n-s%20%5Cright)%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D#card=math&code=E%5Cleft%28%20%7B%20S%20%7D_%7B%20E%20%7D%20%5Cright%29%20%3D%5Cleft%28%20n-s%20%5Cright%29%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D&height=23&width=144)；
  3. 只有当 方差分析 - 图50 为真时，方差分析 - 图51#card=math&code=%5Cfrac%20%7B%20%7B%20S%20%7D%7B%20A%20%7D%20%7D%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%20%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft%28%20s-1%20%5Cright%29&height=41&width=120) ，![](https://g.yuque.com/gr/latex?E%5Cleft(%20%7B%20S%20%7D%7B%20A%20%7D%20%5Cright)%20%3D%5Cleft(%20s-1%20%5Cright)%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D#card=math&code=E%5Cleft%28%20%7B%20S%20%7D%7B%20A%20%7D%20%5Cright%29%20%3D%5Cleft%28%20s-1%20%5Cright%29%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D&height=23&width=142)；而当 方差分析 - 图52 为真时，![](https://g.yuque.com/gr/latex?E%5Cleft(%20%7B%20S%20%7D%7B%20A%20%7D%20%5Cright)%20%3D%5Cleft(%20s-1%20%5Cright)%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%2B%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20s%20%7D%7B%20%7B%20n%20%7D%7B%20j%20%7D%7B%20%5Cdelta%20%20%7D%7B%20j%20%7D%5E%7B%202%20%7D%20%7D%20%3E%5Cleft(%20s-1%20%5Cright)%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D#card=math&code=E%5Cleft%28%20%7B%20S%20%7D%7B%20A%20%7D%20%5Cright%29%20%3D%5Cleft%28%20s-1%20%5Cright%29%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%2B%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20s%20%7D%7B%20%7B%20n%20%7D%7B%20j%20%7D%7B%20%5Cdelta%20%20%7D_%7B%20j%20%7D%5E%7B%202%20%7D%20%7D%20%3E%5Cleft%28%20s-1%20%5Cright%29%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D&height=52&width=314)；

而两个独立方差一般用F检验，所以我们考虑统计量：

方差分析 - 图53%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft(%20n-s%20%5Cright)%20%20%7D%20%7D%20%3D%7B%20%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20A%20%7D%20%7D%2F%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%20%7D%7B%20s-1%20%7D%20%20%7D%2F%7B%20%5Cfrac%20%7B%20%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%20%7D%20%7D%7B%20n-s%20%7D%20%20%7D#card=math&code=F%3D%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20A%20%7D%20%7D%2F%7B%20%5Cleft%28%20s-1%20%5Cright%29%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft%28%20n-s%20%5Cright%29%20%20%7D%20%7D%20%3D%7B%20%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20A%20%7D%20%7D%2F%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%20%7D%7B%20s-1%20%7D%20%20%7D%2F%7B%20%5Cfrac%20%7B%20%7B%20%7B%20%7B%20S%20%7D_%7B%20E%20%7D%20%7D%2F%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%20%7D%20%7D%7B%20n-s%20%7D%20%20%7D&height=48&width=258)

也就是说，当 方差分析 - 图54 不真 方差分析 - 图55 为真时，分子的取值有偏大的趋势，于是拒绝域形式：

方差分析 - 图56%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft(%20n-s%20%5Cright)%20%20%7D%20%7D%20%5Cge%20k#card=math&code=F%3D%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20A%20%7D%20%7D%2F%7B%20%5Cleft%28%20s-1%20%5Cright%29%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D_%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft%28%20n-s%20%5Cright%29%20%20%7D%20%7D%20%5Cge%20k&height=47&width=153)

而由 方差分析 - 图57 与 方差分析 - 图58 独立，当 方差分析 - 图59 为真时，统计量所满足的分布:

方差分析 - 图60#card=math&code=F%5Csim%20F%5Cleft%28%20s-1%2Cn-s%20%5Cright%29&height=20&width=146)

于是，我们加上弃真概率 方差分析 - 图61，可以得到拒绝域：

方差分析 - 图62%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft(%20n-s%20%5Cright)%20%20%7D%20%7D%20%5Cge%20F%5Cleft(%20s-1%2Cn-s%20%5Cright)#card=math&code=F%3D%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20A%20%7D%20%7D%2F%7B%20%5Cleft%28%20s-1%20%5Cright%29%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D_%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft%28%20n-s%20%5Cright%29%20%20%7D%20%7D%20%5Cge%20F%5Cleft%28%20s-1%2Cn-s%20%5Cright%29&height=47&width=255)

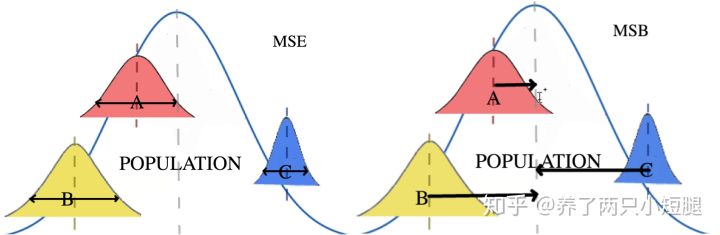
其实，这里的分子和分母就是其他常见解释中的 MSB 和 MSE：

平方和 表达式 均方 方差 简称 表达式 缩写
方差分析 - 图63 方差分析 - 图64%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D#card=math&code=%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20s%20%7D%7B%20%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20%7B%20n%20%7D%7B%20j%20%7D%20%7D%7B%20%7B%20%5Cleft%28%20%7B%20X%20%7D%7B%20ij%20%7D-%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D_%7B%20%5Cbullet%20j%20%7D%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D) 方差分析 - 图65 MSB 组间方差 方差分析 - 图66%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%20%20%7D%7B%20n-s%20%7D#card=math&code=%5Cfrac%20%7B%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20s%20%7D%7B%20%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20%7B%20n%20%7D%7B%20j%20%7D%20%7D%7B%20%7B%20%5Cleft%28%20%7B%20X%20%7D%7B%20ij%20%7D-%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D_%7B%20%5Cbullet%20j%20%7D%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%20%20%7D%7B%20n-s%20%7D) Mean Square Between
方差分析 - 图67 方差分析 - 图68%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D#card=math&code=%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20s%20%7D%7B%20%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20%7B%20n%20%7D%7B%20j%20%7D%20%7D%7B%20%7B%20%5Cleft%28%20%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%7B%20%5Cbullet%20j%20%7D-%5Cbar%20%7B%20X%20%7D%20%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D) 方差分析 - 图69 MSE 组内方差 方差分析 - 图70%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%20%20%7D%7B%20s-1%20%7D#card=math&code=%5Cfrac%20%7B%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20s%20%7D%7B%20%5Csum%20%7B%20j%3D1%20%7D%5E%7B%20%7B%20n%20%7D%7B%20j%20%7D%20%7D%7B%20%7B%20%5Cleft%28%20%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%7B%20%5Cbullet%20j%20%7D-%5Cbar%20%7B%20X%20%7D%20%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%20%20%7D%7B%20s-1%20%7D) Mean Square Error

双因素试验的方差分析

双因素等重复试验的方差分析—有相互作用

前提

  1. 方差分析 - 图71 两因素作用与试验的指标；
  2. 方差分析 - 图72 有 方差分析 - 图73 个水平；
  3. 方差分析 - 图74 有 方差分析 - 图75 个水平；
  4. 对 方差分析 - 图76 的水平的每对组合都做 方差分析 - 图77#card=math&code=t%28t%E2%89%A52%29&height=20&width=56)次试验（称为等重复试验）。
  5. 方差分析 - 图78 之间可能有相互作用。

参数与记号

方差分析 - 图79%20%2Ci%3D1%2C2%2C…%2Cr%3Bj%3D1%2C2%2C…%2Cs%3Bk%3D1%2C2%2C…t#card=math&code=%7B%20X%20%7D%7B%20ijk%20%7D%5Csim%20N%5Cleft%28%20%7B%20%5Cmu%20%20%7D%7B%20ij%20%7D%2C%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%5Cright%29%20%2Ci%3D1%2C2%2C…%2Cr%3Bj%3D1%2C2%2C…%2Cs%3Bk%3D1%2C2%2C…t&height=25&width=445)

方差分析 - 图80，方差分析 - 图81 均为未知参数

总平均 方差分析 - 图82

方差分析 - 图83

方差分析 - 图84

水平 方差分析 - 图85 的效应 方差分析 - 图86

水平 方差分析 - 图87 的效应 方差分析 - 图88

方差分析 - 图89%20%3D%5Cmu%20%2B%7B%20%5Calpha%20%20%7D%7B%20i%20%7D%2B%7B%20%5Cbeta%20%20%7D%7B%20j%20%7D%2B%7B%20%5Cgamma%20%20%7D%7B%20ij%20%7D#card=math&code=%7B%20%5Cmu%20%20%7D%7B%20ij%20%7D%3D%5Cmu%20%2B%7B%20%5Calpha%20%20%7D%7B%20i%20%7D%2B%7B%20%5Cbeta%20%20%7D%7B%20j%20%7D%2B%5Cleft%28%20%7B%20%5Cmu%20%20%7D%7B%20ij%20%7D-%7B%20%5Cmu%20%20%7D%7B%20i%5Cbullet%20%20%7D-%7B%20%5Cmu%20%20%7D%7B%20%5Cbullet%20j%20%7D%2B%5Cmu%20%20%5Cright%29%20%3D%5Cmu%20%2B%7B%20%5Calpha%20%20%7D%7B%20i%20%7D%2B%7B%20%5Cbeta%20%20%7D%7B%20j%20%7D%2B%7B%20%5Cgamma%20%20%7D%7B%20ij%20%7D&height=24&width=446)

方差分析 - 图90

方差分析 - 图91

方差分析 - 图92

方差分析 - 图93

总结：

方差分析 - 图94

方差分析 - 图95#card=math&code=%7B%20%5Cvarepsilon%20%20%7D%7B%20ijk%20%7D%5Csim%20N%5Cleft%28%200%2C%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%5Cright%29&height=24&width=113)，各 ![](https://g.yuque.com/gr/latex?%5Cvarepsilon%7Bij%7D#card=math&code=%5Cvarepsilon_%7Bij%7D&height=16&width=18) 独立

方差分析 - 图96

方差分析 - 图97

假设

方差分析 - 图98

方差分析 - 图99

方差分析 - 图100

双因素试验的方差分析表

与单因素情况类似，对这些问题的检验方法也是建立在平方和的分解上的，思路是一样的，但由于较复杂，我们直接给出方差分析表：

方差来源 平方和 自由度 均方 F比
因素A 方差分析 - 图101 r-1 方差分析 - 图102 方差分析 - 图103
因素B 方差分析 - 图104 s-1 方差分析 - 图105 方差分析 - 图106
交互作用 方差分析 - 图107 (r-1)(s-1) 方差分析 - 图108%20%5Cleft(%20s-1%20%5Cright)%20%20%7D#card=math&code=%7B%20%5Cbar%20%7B%20S%20%7D%20%20%7D%7B%20A%C3%97B%20%7D%3D%5Cfrac%20%7B%20%7B%20S%20%7D%7B%20A%C3%97B%20%7D%20%7D%7B%20%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%20%7D) 方差分析 - 图109
误差 方差分析 - 图110 rs(t-1) 方差分析 - 图111%20%20%7D#card=math&code=%7B%20%5Cbar%20%7B%20S%20%7D%20%20%7D%7B%20E%20%7D%3D%5Cfrac%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%7B%20rs%5Cleft%28%20t-1%20%5Cright%29%20%20%7D)
总和 方差分析 - 图112 rst-1

拒绝域

同单因素方差分析类似，这里只做总结：

  1. 当 方差分析 - 图113 为真时，可以证明 方差分析 - 图114%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft(%20rs%5Cleft(%20t-1%20%5Cright)%20%20%5Cright)%20%20%7D%20%7D%20%5Csim%20F%5Cleft(%20r-1%2Crs%5Cleft(%20t-1%20%5Cright)%20%20%5Cright)#card=math&code=%7B%20F%20%7D%7B%20A%20%7D%3D%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20A%20%7D%20%7D%2F%7B%20%5Cleft%28%20r-1%20%5Cright%29%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft%28%20rs%5Cleft%28%20t-1%20%5Cright%29%20%20%5Cright%29%20%20%7D%20%7D%20%5Csim%20F%5Cleft%28%20r-1%2Crs%5Cleft%28%20t-1%20%5Cright%29%20%20%5Cright%29&height=47&width=320)
    取显著性水平为 方差分析 - 图115，得到假设 方差分析 - 图116 的拒绝域为：方差分析 - 图117%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft(%20rs%5Cleft(%20t-1%20%5Cright)%20%20%5Cright)%20%20%7D%20%7D%20%5Cge%20F%5Cleft(%20r-1%2Crs%5Cleft(%20t-1%20%5Cright)%20%20%5Cright)#card=math&code=%7B%20F%20%7D%7B%20A%20%7D%3D%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20A%20%7D%20%7D%2F%7B%20%5Cleft%28%20r-1%20%5Cright%29%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft%28%20rs%5Cleft%28%20t-1%20%5Cright%29%20%20%5Cright%29%20%20%7D%20%7D%20%5Cge%20F%5Cleft%28%20r-1%2Crs%5Cleft%28%20t-1%20%5Cright%29%20%20%5Cright%29&height=47&width=320)
  2. 当 方差分析 - 图118 为真时，可以证明 方差分析 - 图119%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft(%20rs%5Cleft(%20t-1%20%5Cright)%20%20%5Cright)%20%20%7D%20%7D%20%5Csim%20F%5Cleft(%20s-1%2Crs%5Cleft(%20t-1%20%5Cright)%20%20%5Cright)#card=math&code=%7B%20F%20%7D%7B%20B%20%7D%3D%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20B%20%7D%20%7D%2F%7B%20%5Cleft%28%20s-1%20%5Cright%29%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft%28%20rs%5Cleft%28%20t-1%20%5Cright%29%20%20%5Cright%29%20%20%7D%20%7D%20%5Csim%20F%5Cleft%28%20s-1%2Crs%5Cleft%28%20t-1%20%5Cright%29%20%20%5Cright%29&height=47&width=321)
    取显著性水平为 方差分析 - 图120，得到假设 方差分析 - 图121的 拒绝域为：方差分析 - 图122%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft(%20rs%5Cleft(%20t-1%20%5Cright)%20%20%5Cright)%20%20%7D%20%7D%20%5Cge%20F%5Cleft(%20s-1%2Crs%5Cleft(%20t-1%20%5Cright)%20%20%5Cright)#card=math&code=%7B%20F%20%7D%7B%20B%20%7D%3D%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20B%20%7D%20%7D%2F%7B%20%5Cleft%28%20s-1%20%5Cright%29%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft%28%20rs%5Cleft%28%20t-1%20%5Cright%29%20%20%5Cright%29%20%20%7D%20%7D%20%5Cge%20F%5Cleft%28%20s-1%2Crs%5Cleft%28%20t-1%20%5Cright%29%20%20%5Cright%29&height=47&width=321)
  3. 当 方差分析 - 图123 为真时，可以证明 方差分析 - 图124%20%5Cleft(%20s-1%20%5Cright)%20%20%5Cright)%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft(%20rs%5Cleft(%20t-1%20%5Cright)%20%20%5Cright)%20%20%7D%20%7D%20%5Csim%20F%5Cleft(%20%5Cleft(%20r-1%20%5Cright)%20%5Cleft(%20s-1%20%5Cright)%20%2Crs%5Cleft(%20t-1%20%5Cright)%20%20%5Cright)#card=math&code=%7B%20F%20%7D%7B%20A%C3%97B%20%7D%3D%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20A%C3%97B%20%7D%20%7D%2F%7B%20%5Cleft%28%20%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%20%5Cright%29%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft%28%20rs%5Cleft%28%20t-1%20%5Cright%29%20%20%5Cright%29%20%20%7D%20%7D%20%5Csim%20F%5Cleft%28%20%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%2Crs%5Cleft%28%20t-1%20%5Cright%29%20%20%5Cright%29&height=47&width=461)
    取显著性水平为 方差分析 - 图125，得到假设 方差分析 - 图126 的拒绝域为：方差分析 - 图127%20%5Cleft(%20s-1%20%5Cright)%20%20%5Cright)%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft(%20rs%5Cleft(%20t-1%20%5Cright)%20%20%5Cright)%20%20%7D%20%7D%20%5Cge%20F%5Cleft(%20%5Cleft(%20r-1%20%5Cright)%20%5Cleft(%20s-1%20%5Cright)%20%2Crs%5Cleft(%20t-1%20%5Cright)%20%20%5Cright)#card=math&code=%7B%20F%20%7D%7B%20A%C3%97B%20%7D%3D%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20A%C3%97B%20%7D%20%7D%2F%7B%20%5Cleft%28%20%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%20%5Cright%29%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft%28%20rs%5Cleft%28%20t-1%20%5Cright%29%20%20%5Cright%29%20%20%7D%20%7D%20%5Cge%20F%5Cleft%28%20%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%2Crs%5Cleft%28%20t-1%20%5Cright%29%20%20%5Cright%29&height=47&width=461)

双因素无重复试验的方差分析—无相互作用

前提

  1. A，B两因素作用与试验的指标；
  2. A有r个水平；
  3. B有s个水平；
  4. 对A，B的水平的每对组合都做 1 次试验。
  5. A，B之间不存在相互作用或很小可以忽略。

参数与记号

方差分析 - 图128

方差分析 - 图129#card=math&code=%7B%20%5Cvarepsilon%20%20%7D%7B%20ijk%20%7D%5Csim%20N%5Cleft%28%200%2C%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%5Cright%29&height=24&width=113)，各 ![](https://g.yuque.com/gr/latex?%5Cvarepsilon%7Bijk%7D#card=math&code=%5Cvarepsilon_%7Bijk%7D&height=16&width=24) 独立

方差分析 - 图130

方差分析 - 图131

假设

方差分析 - 图132

方差分析 - 图133

双因素试验的方差分析表

与单因素情况类似，对这些问题的检验方法也是建立在平方和的分解上的，思路是一样的，但由于较复杂，我们直接给出方差分析表：

方差来源 平方和 自由度 均方 F比
因素A 方差分析 - 图134 r-1 方差分析 - 图135 方差分析 - 图136
因素B 方差分析 - 图137 s-1 方差分析 - 图138 方差分析 - 图139
误差 方差分析 - 图140 (r-1)(s-1) 方差分析 - 图141%20%5Cleft(%20s-1%20%5Cright)%20%20%7D#card=math&code=%7B%20%5Cbar%20%7B%20S%20%7D%20%20%7D%7B%20E%20%7D%3D%5Cfrac%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%7B%20%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%20%7D)
总和 方差分析 - 图142 rs-1

拒绝域

同单因素方差分析类似，这里只做总结：

  1. 当 方差分析 - 图143 为真时，可以证明 方差分析 - 图144%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft(%20%5Cleft(%20r-1%20%5Cright)%20%5Cleft(%20s-1%20%5Cright)%20%20%5Cright)%20%20%7D%20%7D%20%5Csim%20F%5Cleft(%20r-1%2C%5Cleft(%20r-1%20%5Cright)%20%5Cleft(%20s-1%20%5Cright)%20%20%5Cright)#card=math&code=%7B%20F%20%7D%7B%20A%20%7D%3D%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20A%20%7D%20%7D%2F%7B%20%5Cleft%28%20r-1%20%5Cright%29%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft%28%20%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%20%5Cright%29%20%20%7D%20%7D%20%5Csim%20F%5Cleft%28%20r-1%2C%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%20%5Cright%29&height=47&width=392)
    取显著性水平为 方差分析 - 图145，得到假设 方差分析 - 图146 的拒绝域为：方差分析 - 图147%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft(%20%5Cleft(%20r-1%20%5Cright)%20%5Cleft(%20s-1%20%5Cright)%20%20%5Cright)%20%20%7D%20%7D%20%5Cge%20F%5Cleft(%20r-1%2C%5Cleft(%20r-1%20%5Cright)%20%5Cleft(%20s-1%20%5Cright)%20%20%5Cright)#card=math&code=%7B%20F%20%7D%7B%20A%20%7D%3D%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20A%20%7D%20%7D%2F%7B%20%5Cleft%28%20r-1%20%5Cright%29%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft%28%20%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%20%5Cright%29%20%20%7D%20%7D%20%5Cge%20F%5Cleft%28%20r-1%2C%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%20%5Cright%29&height=47&width=392)
  2. 当 方差分析 - 图148 为真时，可以证明 方差分析 - 图149%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft(%20%5Cleft(%20r-1%20%5Cright)%20%5Cleft(%20s-1%20%5Cright)%20%20%5Cright)%20%20%7D%20%7D%20%5Csim%20F%5Cleft(%20s-1%2C%5Cleft(%20r-1%20%5Cright)%20%5Cleft(%20s-1%20%5Cright)%20%20%5Cright)#card=math&code=%7B%20F%20%7D%7B%20B%20%7D%3D%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20B%20%7D%20%7D%2F%7B%20%5Cleft%28%20s-1%20%5Cright%29%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft%28%20%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%20%5Cright%29%20%20%7D%20%7D%20%5Csim%20F%5Cleft%28%20s-1%2C%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%20%5Cright%29&height=47&width=392)
    取显著性水平为 方差分析 - 图150，得到假设 方差分析 - 图151 的拒绝域为：方差分析 - 图152%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft(%20%5Cleft(%20r-1%20%5Cright)%20%5Cleft(%20s-1%20%5Cright)%20%20%5Cright)%20%20%7D%20%7D%20%5Cge%20F%5Cleft(%20s-1%2C%5Cleft(%20r-1%20%5Cright)%20%5Cleft(%20s-1%20%5Cright)%20%20%5Cright)#card=math&code=%7B%20F%20%7D%7B%20B%20%7D%3D%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%20B%20%7D%20%7D%2F%7B%20%5Cleft%28%20s-1%20%5Cright%29%20%20%7D%20%7D%7B%20%7B%20%7B%20S%20%7D%7B%20E%20%7D%20%7D%2F%7B%20%5Cleft%28%20%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%20%5Cright%29%20%20%7D%20%7D%20%5Cge%20F%5Cleft%28%20s-1%2C%5Cleft%28%20r-1%20%5Cright%29%20%5Cleft%28%20s-1%20%5Cright%29%20%20%5Cright%29&height=47&width=392)