3 子空间的交，和与直和

矩阵的秩

上一节介绍了向量组的秩，即向量组的极大线性无关组所含向量的个数，而矩阵的每一列（每一行）也可以看成一个列向量（行向量），这一节即讨论矩阵的列（行）向量组的秩。

设 是数域 上一个 矩阵， 的每一列是一个 元有序数组，它是 中的一个向量，依次记作 ，称它们为 的列向量组。 的每一行是一个 元有序数组，它是 中的一个向量，依次记作 ，称它们为 的行向量组。

的列秩 ， 是 的列空间。

的行秩 ， 是 的行空间。

一个最关键的问题来了，矩阵的列秩和行秩之间有什么联系？

我们是这样一步一步解决这个问题的：

1. 探索阶梯型矩阵的列秩与行秩之间的关系；
2. 探索矩阵的初等变换是否改变矩阵的行秩和列秩；
3. 通过 1 和 2 得到的结论再间接得到矩阵的列秩和行秩之间的关系。

对于 1 我们有以下【P88】的定理：

【定理 1】数域 上阶梯型矩阵 的列秩与行秩相等，它们都等于 的非零行的个数；并且 的主元所在的列构成 的列向量组的一个极大线性无关组。

对于 2 我们有以下定理：

【定理 2】矩阵的初等行变换不改变矩阵的行秩。

【定理 3】矩阵的初等行变换不改变矩阵的列向量组的线性相关性，从而不改变矩阵的列秩；并且设矩阵 经过初等行变换变成矩阵 ，则 的 列构成 的列向量组的一个极大线性无关组当且仅当 的 列构成 的列向量组的一个极大线性无关组。

这三个定理的推导过程十分重要，书中也做了详细的阐述，这里不再赘述。由这些定理可以得到：

【定理 4】 的行秩 的行秩 的列秩 的列秩，所以任一矩阵 的行秩等于 的列秩。

我们把矩阵 的行秩与列秩统称为矩阵 的秩，记作 #card=math&code=rank%28A%29&height=16&width=49)。

同时，由于矩阵 的行向量组是它的转置 的列向量组，因此可以得到，矩阵的初等列变换也不改变矩阵的秩。

子式的最高阶数

上面是以矩阵的列向量组或行向量组的极大线性无关组的个数来刻画矩阵的秩，我们还可以通过矩阵的子式的最高阶数来刻画矩阵的秩。

矩阵 的一个 阶子式为：

%0A%5Ctag%7B21%7D%0A#card=math&code=A%5Cleft%28%5Cbegin%7Bmatrix%7D%0Ak_1%2C…%2Ck_m%5C%5C%0Al_1%2C…%2Cl_m%0A%5Cend%7Bmatrix%7D%5Cright%29%0A%5Ctag%7B21%7D%0A&height=36&width=583)

我们有【定理 5】，任一非零矩阵的秩等于它的不为零的子式的最高阶数。

定理 4 和定理 5 表明，在一非零矩阵 的行秩等于列秩，并且等于 的不为零的子式的最高阶数。由此可以看出，矩阵的秩是一个非常深刻的概念，它可以从行向量组的秩，列向量组的秩，不为零子式的最高阶数三个角度来刻画。此外， 的秩等于 的列空间的维数，也等于 的行空间的维数。对于一个 矩阵 来说， 的列空间是 的一个子空间，而 的行空间是 的一个子空间，它们的维数竟然相等！而且还等于 的不为零子式的最高阶数！这是多么的神奇。

最后，如果 级矩阵 的秩等于 ，那么称 是满秩矩阵，满秩矩阵的充要条件是 。

矩阵秩的作用

我们回过头再看看定理 1 和定理 3 ，它们都有两部分，将各自的后面部分合起来就能得到以下十分重要的推论：

【推论】设矩阵 经过初等行变换化成阶梯型矩阵 ， 则 的秩等于 的非零行个数。设 的主元位于第 列，则 的第 列构成 的列向量组的一个极大线性无关组。

这个结论十分有用！

这个推论给出了同时求出矩阵的秩和它的列向量组的一个极大线性无关组的方法。这个方法也可以用来求 中向量组的秩和它的一个极大线性无关组，只要把每个向量写成列向量，并且组成一个矩阵。这个方法还可以用来求 中向量组生成的子空间的维数和一个基。

这个推论还告诉我们，尽管矩阵 经过不同的初等行变换化成的阶梯形矩阵可能不相等，比如有的是阶梯型矩阵，有的是简化阶梯型矩阵，但这些阶梯型矩阵的非零行个数是相等的，都等于矩阵 的秩。

而同样，根据定理 5，利用最高阶的不等于 0 的子式，也可以求出矩阵的列（行）向量组的一个极大线性无关组。即有下述结论：

【推论】设 矩阵 的秩为 ，则 不等于零的 阶子式所在的列（行）构成 的列（行）向量组的一个极大线性无关组。

线性方程组的解

在学习了线性空间及其子空间的基和维数后，一个重要的应用就是解线性方程组。关于齐次线性方程组和非齐次线性方程组的解的判别准则和解的结构，在《MIT线性代数4-8》这篇文章中已经提到，所以这里不再赘述。

子空间的交

接下来探索通过线性空间 的子空间的运算来研究 的结构。

类比几何空间中，过定点 的两个平面 与 的交是过点 的一条直线，这表明几何空间中两个子空间的交仍是一个子空间。线性空间也有也似的结论：设 ， 都是数域 上线性空间 的子空间，则 也是 的子空间。

由集合的交的运算法则，立即得出子空间的交的运算法则满足交换律和结合律。

由结合律可以定义多个子空间的交：设 都是 的子空间，则 也是 的子空间，记作 。

设 是一个指标集，对于每个 是 的子空间，令

同样， 也是 的子空间。

子空间的和

上面讨论了子空间的交，那么自然而然接着想到子空间的并，但类比在几何空间中（如下图）， 不是几何空间的子空间，这是因为对于 ，有 。

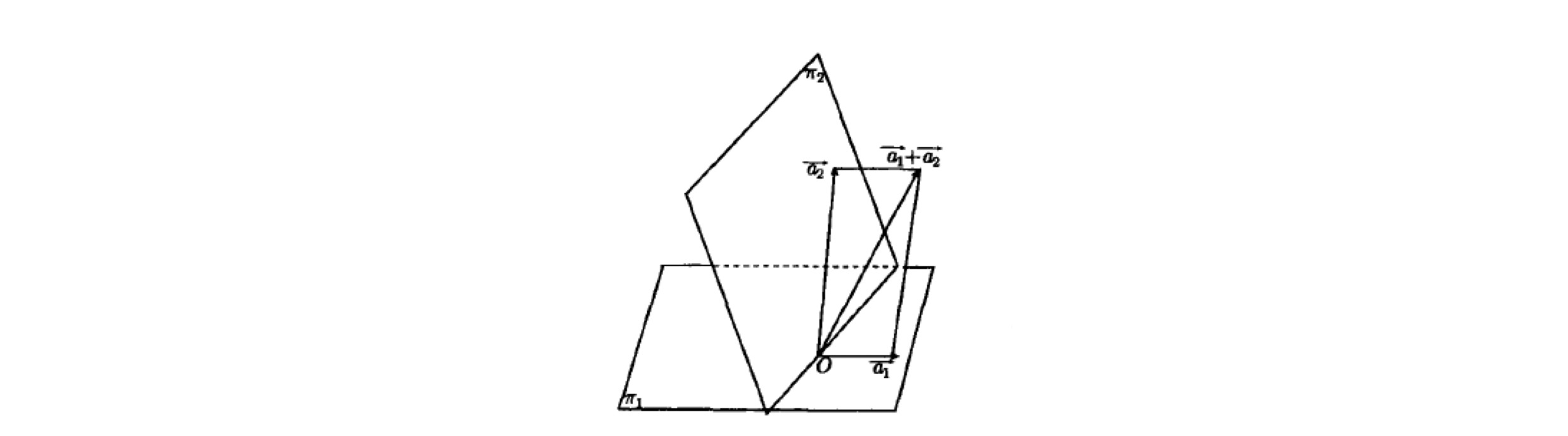
为了构建包含 的子空间 与 的并集 的一个子空间，那么这个子空间应该包含下述集合：

把这个集合记作 ，并且有如下定理：

【定理 P107】设 与 都是数域 上线性空间 的子空间，令

则 是 的一个子空间，我们称 是 与 的和。

并且， 是包含 的最小的子空间。同样，子空间的和也满足交换律和结合律。

同样，由由结合律可以定义多个子空间的和：设 都是 的子空间，则 也是 的子空间，记作 ，并且

维数公式

向量组和子空间是密切相关的，线性空间中的向量组可以生成子空间，那么向量组所生成的子空间之间的和可以用向量组表示吗？我们有如下命题：

【命题 P107】设 是数域 上的线性空间， 与 是 的两个向量组，则

我们再看上面的图中，几何空间中任一向量可以表示成 ，其中 。于是 %3D3#card=math&code=dim%28%5Cpi_1%2B%5Cpi_2%29%3D3&height=16&width=103)，又 %3D1#card=math&code=dim%5Cpi_i%3D2%2Ci%3D1%2C2%3B%5Cspace%20dim%28%5Cpi_1%5Ccap%20%5Cpi_2%29%3D1&height=16&width=220)，因此

%3Ddim%5Cpi_1%2Bdim%5Cpi_2-dim(%5Cpi_1%5Ccap%20%5Cpi_2)%0A%5Ctag%7B27%7D%0A#card=math&code=dim%28%5Cpi_1%2B%5Cpi_2%29%3Ddim%5Cpi_1%2Bdim%5Cpi_2-dim%28%5Cpi_1%5Ccap%20%5Cpi_2%29%0A%5Ctag%7B27%7D%0A&height=16&width=583)

由此受到启发，并通过上面给出的命题可以证明以下命题，也就是子空间的维数公式：

【定理 P108】设 都是数域 上线性空间 的有限维子空间，则

%3Ddim%5Cpi_1%2Bdim%5Cpi_2-dim(%5Cpi_1%5Ccap%20%5Cpi_2)%0A%5Ctag%7B28%7D%0A#card=math&code=dim%28%5Cpi_1%2B%5Cpi_2%29%3Ddim%5Cpi_1%2Bdim%5Cpi_2-dim%28%5Cpi_1%5Ccap%20%5Cpi_2%29%0A%5Ctag%7B28%7D%0A&height=16&width=583)

这个定理适用于有限维子空间。另外，这个形式也非常像抽屉原理的公式。

从这个定理可以立即得到

%3Ddim%5Cpi_1%2Bdim%5Cpi_2%20%5Cspace%20%5CLeftrightarrow%20%5Cspace%20V_1%20%5Ccap%20V_2%3D0%0A%5Ctag%7B29%7D%0A#card=math&code=dim%28%5Cpi_1%2B%5Cpi_2%29%3Ddim%5Cpi_1%2Bdim%5Cpi_2%20%5Cspace%20%5CLeftrightarrow%20%5Cspace%20V_1%20%5Ccap%20V_2%3D0%0A%5Ctag%7B29%7D%0A&height=16&width=583)

子空间的直和

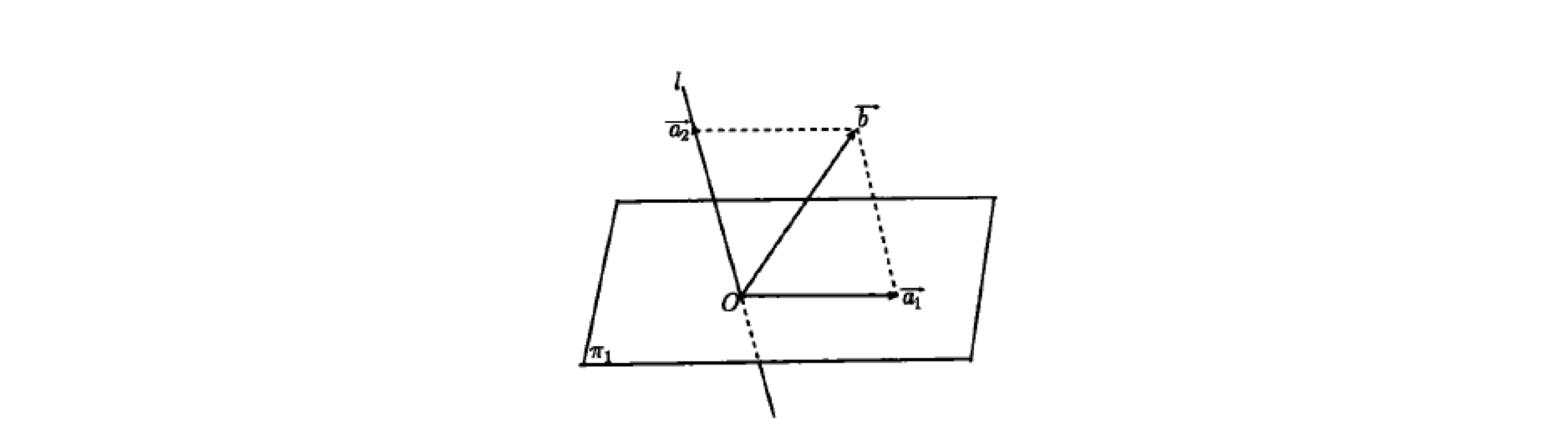
如图几何空间中， 是过定点 的一个平面， 是过定点 的一条直线，并且 不在平面 内，则 等于几何空间。几何空间中任一向量 可以唯一表示成：

由此受到启发，引出直和的概念：

【定义 P109】设 都是数域 上线性空间 的子空间，如果 中每个向量 都能唯一地表示成

那么和 称为直和，记作 。

还是类比几何空间，如上图， 是直和，此时 。这两者之间有必然联系吗？

我们有以下非常重要的定理：

【定理 1 P109】设 都是数域 上线性空间 的子空间，则下列命题等价：

1. 和 是直和；
2. 中零向量的表法唯一，即若 ，则 且 ；
3. ；
4. 的一个基 与 的一个基 合起来是 的一个基。

注意，这里并没有强调子空间必须是有限维子空间，定理中也没有提到子空间的维数。同时，这个命题的证明过程的思路值得好好看看。

以上结论结合维数定理，我们有以下定理：

【定理 2 P110】设 都是数域 上线性空间 的有限维子空间，则 是直和当且仅当

%3DdimV_1%2BdimV_2%0A%5Ctag%7B32%7D%0A#card=math&code=dim%28V_1%2BV_2%29%3DdimV_1%2BdimV_2%0A%5Ctag%7B32%7D%0A&height=16&width=583)

多个子空间的直和

多个子空间的和也可以讨论直和问题。

【定义 P111】设 都是数域 上线性空间 的子空间，如果 中每个向量 都能唯一地表示成

那么和 称为直和，记作 ，或 。

还是类比两个子空间的直和，我们有以下结论：

【定理 3 P111】设 都是数域 上线性空间 的子空间，则下列命题等价：

1. 和 是直和；
2. 和 中零向量的表法唯一；
3. %3D0%2Ci%3D1%2C2%2C%5Ccdots%2Cm#card=math&code=V_i%5Ccap%28%20%5Cunderset%20%7B%20j%5Cneq%20i%20%7D%7B%20%5CSigma%20%20%7D%20V_j%29%3D0%2Ci%3D1%2C2%2C%5Ccdots%2Cm&height=24&width=181)；
4. 的一个基 ， 的一个基 ，， 的一个基 ， 合起来是 的一个基。

以上结论结合维数定理，我们有以下定理：

【定理 4 P112】设 都是数域 上线性空间 的有限维子空间，则 是直和当且仅当

%3D%5Coverset%20%7Bm%7D%7B%20%5Cunderset%20%7Bi%3D1%7D%7B%20%5CSigma%20%7D%20%20%7DdimV_i%0A%5Ctag%7B34%7D%0A#card=math&code=dim%28V_1%2BV_2%2B%5Ccdots%2BV_m%29%3D%5Coverset%20%7Bm%7D%7B%20%5Cunderset%20%7Bi%3D1%7D%7B%20%5CSigma%20%7D%20%20%7DdimV_i%0A%5Ctag%7B34%7D%0A&height=30&width=583)

定理 3 揭示了可以利用子空间的运算来研究线性空间的结构：如果 等于它的若干个子空间 的直和：，那么 的一个基， 的一个基，， 的一个基， 合起来就是 的一个基。

这就是研究线性空间的第二条途径。

补空间

再观察几何空间中，几何空间等于 ，且 是直和，此时称几何空间是平面 与直线 的直和，并且称 是 的一个补空间，称 是 的一个补空间。类比几何空间补空间的概念，引出子空间的补空间的概念：

【定义 P111】设 都是数域 上线性空间 的子空间，如果 且 是直和，那么称 是 与 的直和，记作 ；此时称 是 的补空间，称 是 的补空间。

上图的几何空间中，任何一条过点 且不在平面 内的直线都是 的补空间。由此看出一个子空间的补空间不唯一。因此，从 且 推不出 ，这一点希望注意。

有限维的线性空间 的任一子空间都有补空间，无限维线性空间 的任一子空间也有补空间。