XGBoost可以看作是对GradientBoost的优化。其原理还是基于GradientBoost，它的创新之处是用了二阶导数和正则项。

回归树与集成学习

回归树回顾

回归树，也称为分类与回归树（Classification And Regression Tree，CART）：

• 决策规则与决策树相同；
• 每一个叶节点包含一个值。

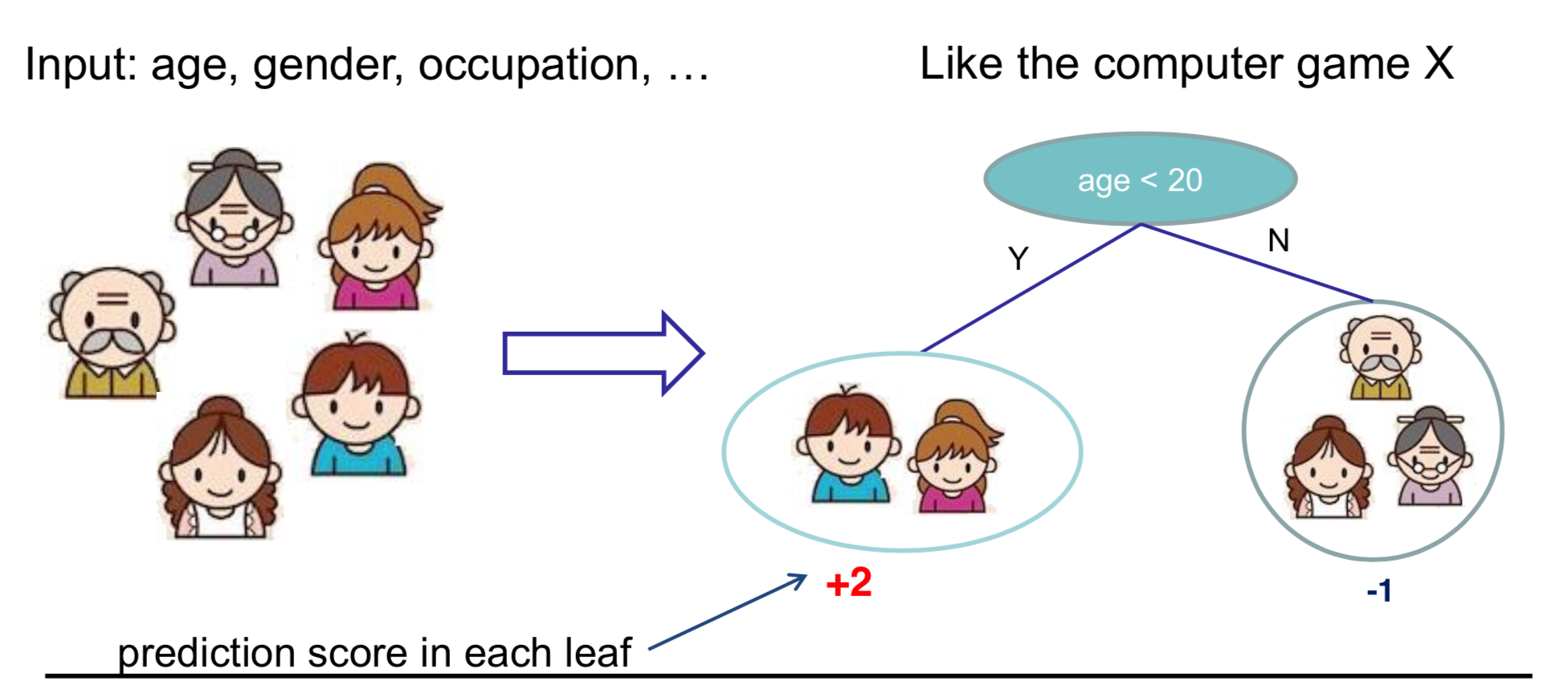
回归树的优势

树的集成方法有很多优势：

• 应用广泛，比如 GBM 和随机森林等。几乎一半的数据挖掘比赛获胜者都是靠树的集成方法取胜的。
• 你不需要将特征标准化，因为做不做输入特征缩放结果是一样的。
• 能够学习到更多特征之间的高阶关系。
• 具有可扩放行（scalable)，应用于工业界。

可扩放性(Scalability)是指问题规模和处理器数目之间的函数关系。

可扩放性实际上是和并行算法以及并行计算机体系结构放在一起讨论的。某个算法在某个机器上的可扩放性反映该算法是否能有效利用不断增加的CPU。我们研究可扩放性的目的就是要使算法尽可能的利用最多的处理器，并且我们也可以预测当某个算法移植到大规模处理机上后的运行效果（即问题规模扩大时对处理器的利用情况）。

模型与参数

模型：假设有 棵树：

是包含所有回归树的函数空间。注意，回归树可以看做一个将属性映射为数值的函数。

参数：

• 包含每棵树的结构和叶子节点的值。
• 也可以用函数作为参数：
• 我们学习的是函数（树），而不是学习 空间中的权重。

单变量回归树

输入特征通常很多，但是回归树中每个节点其实都只对一个特征进行分析，所以研究单变量回归树很有意义。

以下以单变量决策树的学习过程为例来帮助我们理解如何学习回归树，具体过程其实就是定义目标（包括损失函数和正则函数），然后优化这个目标。

举个例子，考虑以时间 time 作为单变量输入的回归树，我想预测在 时间点我是否喜爱浪漫的音乐。

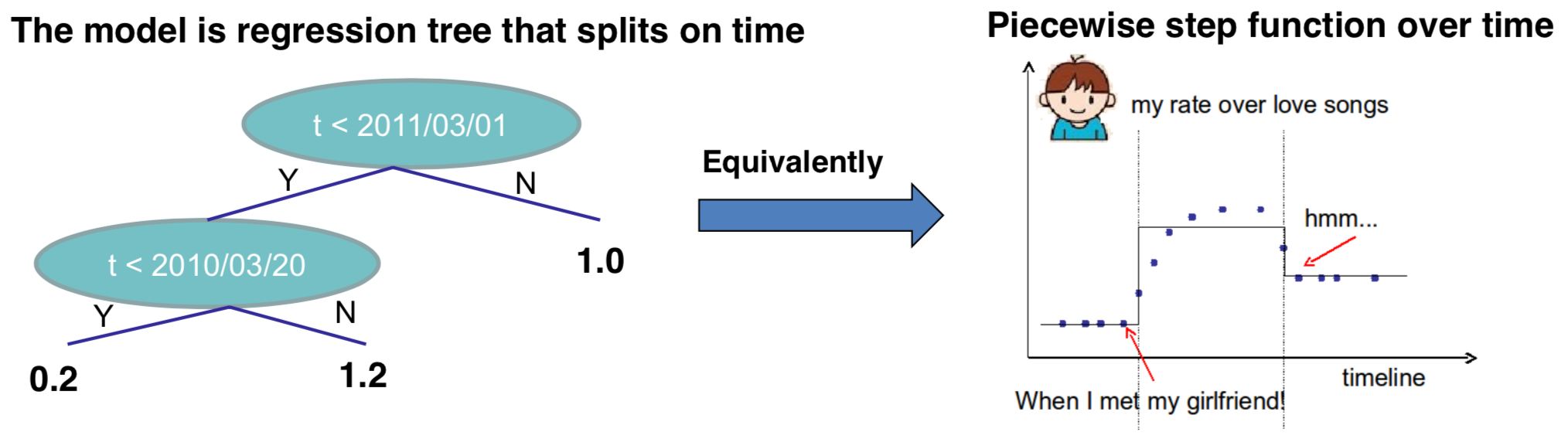
我们需要学习一个阶跃函数（Step function）：

单变量回归树的目标也是包括：

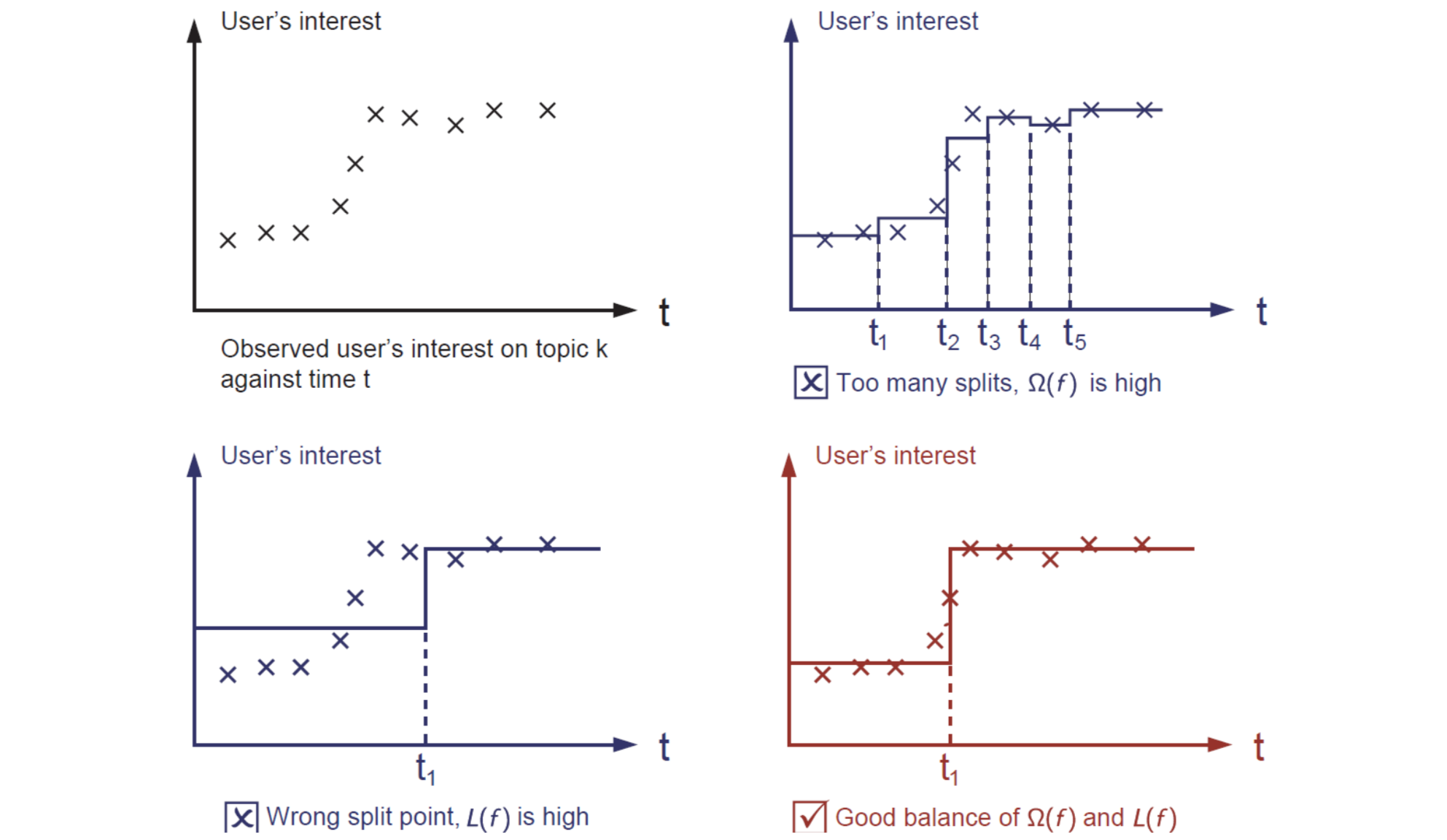
• 训练误差：在数据集上，函数拟合得怎么样？
• 正则函数：我们如何定义函数的复杂度？答案是分隔点的数量，以及每一部分高度的 L2 范数。

以下是学习阶跃函数的过程：

集成树的目标

我们再回到集成树的模型和目标：

模型：假设有 棵树

目标：

定义 可能的方式?

• 树的节点的数量和深度；
• 叶的权重的 L2 范数；
• 其他（后续会提到）。

Objective vs Heuristic

目标最优化与启发式算法

决策树本身是一种启发式的算法，它通过信息增益、剪枝、最大深度和平滑叶结点的值这些方法或参数来构建回归树。

大多数启发式算法对最优化目标函数都能拟合（优化）得很好，我们可以从最优化目标函数的角度来看：

• 信息增益 即 训练误差；
• 剪枝 即 叶子节点数量的正则化
• 最大深度 即 函数空间的限制
• 平滑叶子结点值 即 叶子节点权重的 L2 正则化

回归树用途

回归树的集成决定了你如何预测一个值，它可以用在很多地方，比如分类、回归和排序等等。对于不同的目标函数，回归树的作用也不一样。回顾我们学习过哪些目标函数呢？

• 均方误差（MSE）损失函数，用于大多数梯度提升算法：

• 交叉熵（Cross-entropy）损失函数，用于 LogiBoost：

GBDT

我们从偏差-方差均衡角度引出了损失函数+正则化，并以目标用于回归树的学习。

我们想要得到的是有预测能力且简单的函数（树），这就决定了我们该学习哪些方面——目标函数和模型。

但我们该如何学习呢？

目标函数

我们不能使用比如随机梯度下降（SGD）来得到 ，因为他们是树，而不是数值向量。

这个时候我们前面提到的加法模型和向前分布算法就用到了！

加法模型与前向分步算法

修改一些符号，但本质不变：

在第 轮学习中，，其中 就是我们需要决定的。

目标为找到一个 是之最小。

考虑使用 Square loss 损失函数：

式子中 即为上一轮的残差。

泰特展开损失估计

尽管上面我们用了平方误差作为损失函数让式子变得简单了一些，但目标函数本身还是很麻烦。在GBDT中，我们通常使用损失函数的泰勒二阶展开。

我们回忆泰勒展开并展开损失函数：

只考虑我们在 轮要得到的函数 ，这样，我们可以去除常数项，得到新的目标函数：

为什么我们要花费这么多精力来得到这个目标函数呢？为什么不直接训练回归树呢？

• 理论上，我们可以知道我们在学习什么，是否能够收敛。
• 实际上，回顾监督学习的知识：
  • 和 来自于损失函数的定义；
  • 学习得到我们想要的 仅仅在于目标函数中的 和 ；
  • Think of how you can separate modules of your code when you are asked to implement boosted tree for both sqaure loss and logistic loss.

改进树的定义

我们通过叶子节点的数值向量，和一个将实例映射到叶子节点索引的叶索引应设函数来定义树：

其中， 为叶子节点的总数，从 1 到 T 可以看成叶子节点的索引； 为输入实例的维数； 即将实例映射到具体叶子节点的索引； 是一个 维的向量，即树的叶子节点的权重；那么 即实例 在树中的值。

举例如下，：

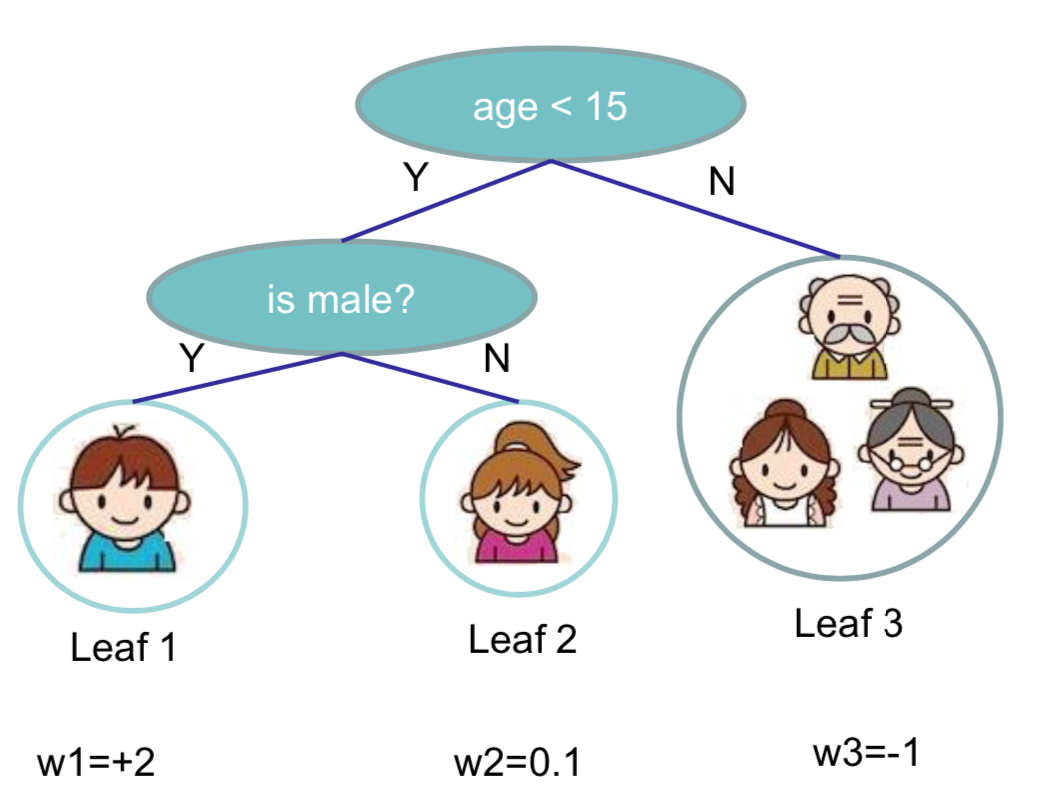
定义树的复杂度

前一项为叶子节点的数目，后一项为叶子节点权重的 L2 范数。上面这棵树的复杂度为：

新的目标

至此，我们可以考虑将上面树和其复杂度的定义应用于目标函数（8）中。

定义树中的叶子节点 的实例集为

这里注意以下，之前的文章中实例集（即训练数据集）的样本容量为 ，但这一节从（4）开始，样本容量（实例总数）用小写 来表示。之前（8）中求和是以实例来求和的，即 ，我们定义了（11）之后，可以换成以叶子节点来对目标函数重新分组。则（8）等价变形为：

这是 个独立的二次函数的和。

目标求解

我们先考虑单变量二次函数：

定义 ，则目标函数继续等价变形：

假设树的结构（即 ）是固定的，那么每个叶子节点的最优权重，以及相应的目标函数的结果就是：

后一项衡量一棵树的结构有多好，通常叫做 Structure Score。以下举例演示这个 Structure Score 的计算：

如上图所述，分数越小，结构越好。

单个树的搜索算法

首先枚举出所有可能的树的结构 ，然后计算树 的 Structure Score：

然后找到最好的树的结构，并得到相应的最优叶子节点的权重：

但是枚举出树的结构本身就是一个问题，因为有无穷多的树。

树的贪心算法

在实际中，我们使用贪心算法来学习回归树：

• 从树的深度 depth=0 开始；
• 对于每棵树的叶子节点，尝试进行一次分枝。分支之后的目标函数的变化为：

这四项分别为左分枝的 score，右分枝的 score，不分枝的 score 以及添加额外的叶子节点所带来的复杂度成本。注意，（16）式中符号为负，这里符号为正，所以是用分枝前的分数减分枝后的分数。

• 还是那个问题：我们怎么找到最好的结构或分枝？

找到最优分枝点的有效方法

分枝规则 的增益到底是什么呢？我们拿输入特征为年龄来举例：

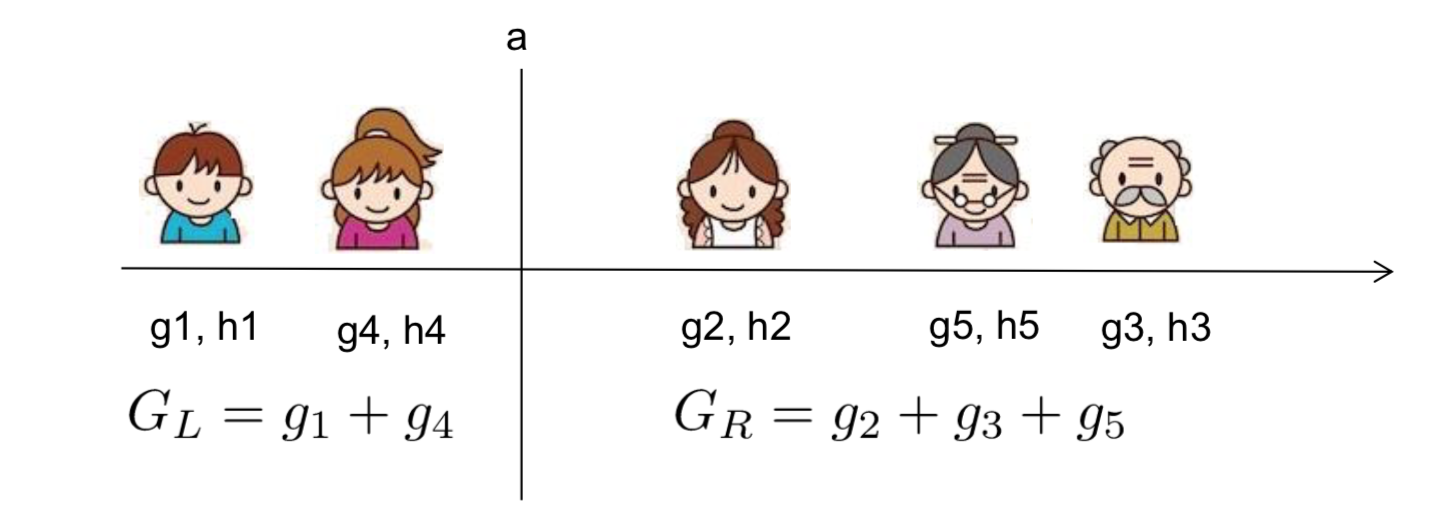
也就是说，我们需要做的只是求出每一边的 和 的和，然后计算下式

在排序后的实例上从左到右线性地扫描就足以决定按此特征的最佳分割。
**

分枝算法

有了以上铺垫，我们就可以总结分枝的算法。

对于每一个节点，枚举出所有输入特征：

• 对于每一个特征，以特征值对实例进行排序；
• 通过线性扫描来决定此特征的最好的分枝点；
• 然后找出所有特征分枝点中最好的那一个进行分枝。

计算生成一个深度为 的树的时间复杂度：

• 时间复杂度为 ：或者说，对于每一层，需要 的时间排序，乘以特征数量 ，因为我们需要生成 层，所以再乘以层数 。
• 这种算法可以进一步优化，比如使用近似或缓存已排序的特征！
• 可以扩展到非常大的数据集。

分类变量

一些树的学习算法会分别学习分类变量与连续型变量。我们可以很容易地使用我们得出的评分公式来对分类变量进行打分。但实际上没必要专门对分类变量分开处理。我们可以使用独热编码（One-hot encoding）的方式对分类变量进行数值向量化。以下生成一个分类变量长度的向量：

如果分类较多，则向量将会很稀疏，该算法是处理稀疏数据的首选算法。

剪枝与正则化

回忆公式（18），当训练误差的减少量 < 正则化系数时，增益 gain 就是负的。所以我们需要在模型的可预测性和复杂度之间做好权衡。

可以采用 Pre-stopping 的方法：

• 当最优的分枝是负增益时，停止分枝；
• 但也有可能不停止分枝，之后的分枝更有作用。

还可以采用 Post-prunning 的方法：生成一棵达到最大深度的树，然后递归地修剪那些负增益的叶分枝。

总结GBDT

• 在每一次迭代中增加一棵新树；
• 在每一次迭代时，计算：

• 然后使用贪心算法生成一棵树

• 将这颗树 添加到模型 中
  • 然而通常，我们是这样做的
  • 称为 step-size 或 shrinkage，通常设定为 0.1 左右；
  • 这意味着在每一步我们不需要做到充分的优化，而是保留了未来继续优化的机会，这对于防止过拟合是非常有帮助的。

总结

思考以下问题来检查你是否学会了GBDT

1. 我们如何建立一棵提升树分类器来解决加权回归问题，即每一个实例都有一个权重？

定义目标函数，计算 ，用它来训练我们已有的非权重版本旧的树的生成算法：

再思考如果考虑将模型和目标函数的分离开来，这个理论如何帮助更好地组织机器学习工具包。

1. 回到时间序列问题，如果我想生成一个关于时间的阶跃函数（Step function，上文这里提到过）。除了自上而下分割方法（top down split approach），有没有其他的方法来进行时间分割（time splits）

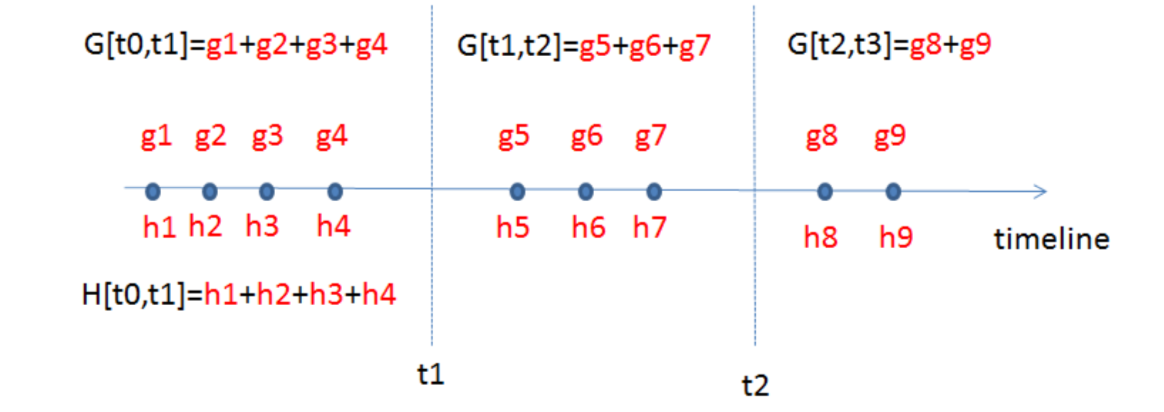
重要的是分割的 structure score：

• 还是和树一样的Top-down greedy；
• Botton-up greedy：从将单个点作为各自分组开始，然后贪心地将临近的点融合；
• 动态规划可以找到这个问题的最优解。

总结

将模型、目标函数和参数分离开来，对我们理解和定制化学习模型非常有用。

方差-偏差均衡随处可见，包括在函数空间学习过程中：

我们需要对我们所学和如何学习保持专业性。清晰的理论认识可以用来更好地指导实际应用。

参考文献

1. homes.cs.washington.edu/~tqchen/pdf/BoostedTree.pdf
2. Greedy function approximation a gradient boosting machine. J.H. Friedman First paper about gradient boosting
3. Stochastic Gradient Boosting. J.H. Friedman. Introducing bagging trick to gradient boosting
4. Elements of Statistical Learning. T. Hastie, R. Tibshirani and J.H. Friedman. Contains a chapter about gradient boosted boosting
5. Additive logistic regression a statistical view of boosting. J.H. Friedman T. Hastie R. Tibshirani. Uses second-order statistics for tree splitting, which is closer to the view presented in this slide
6. Learning Nonlinear Functions Using Regularized Greedy Forest. R. Johnson and T. Zhang. Proposes to do fully corrective step, as well as regularizing the tree complexity. The regularizing trick is closed related to the view present in this slide
7. Software implementing the model described in this slide: https://github.com/tqchen/xgboost
8. https://blog.csdn.net/qq_29831163/article/details/88930389#4%20%E5%B0%8F%E7%BB%93
9. https://zhuanlan.zhihu.com/p/29765582