Classification and logistic regression

接下来咱们讲一下分类的问题。分类问题其实和回归问题很像，只不过我们现在要来预测的 的值只局限于少数的若干个离散值。眼下咱们首先关注的是二值化分类 问题，也就是说咱们要判断的 只有两个取值， 或者 。（咱们这里谈到的大部分内容也都可以扩展到多种类的情况。）例如，假如要建立一个垃圾邮件筛选器，那么就可以用 %7D#card=math&code=x%5E%7B%28i%29%7D&height=16&width=20) 表示一个邮件中的若干特征，然后如果这个邮件是垃圾邮件， 就设为，否则 为 。 也可以被称为消极类别（negative class），而 就成为积极类别（positive class），有的情况下也分别表示成“-” 和 “+”。对于给定的一个 %7D#card=math&code=x%5E%7B%28i%29%7D&height=16&width=20)，对应的%7D#card=math&code=y%5E%7B%28i%29%7D&height=18&width=18)也称为训练样本的标签（label）。

2.1 逻辑回归（Logistic regression）

我们当然也可以还按照之前的线性回归的算法来根据给定的 来预测 ，只要忽略掉 是一个散列值就可以了。然而，这样构建的例子很容易遇到性能问题，这个方法运行效率会非常低，效果很差。而且从直观上来看，#card=math&code=h_%5Ctheta%28x%29&height=16&width=32) 的值如果大于 或者小于 就都没有意义了，因为咱们已经实现都确定了 ，就是说 必然应当是 和 这两个值当中的一个。

所以咱们就改变一下假设函数#card=math&code=h_%5Ctheta%20%28x%29&height=16&width=32) 的形式，来解决这个问题。比如咱们可以选择下面这个函数：

%20%3D%20g(%5Ctheta%5ET%20x)%20%3D%20%5Cfrac%20%201%7B1%2Be%5E%7B-%5Ctheta%5ETx%7D%7D%0A#card=math&code=h_%5Ctheta%28x%29%20%3D%20g%28%5Ctheta%5ET%20x%29%20%3D%20%5Cfrac%20%201%7B1%2Be%5E%7B-%5Ctheta%5ETx%7D%7D%0A&height=35&width=167)

其中有：

%3D%20%5Cfrac%201%20%7B1%2Be%5E%7B-z%7D%7D%0A#card=math&code=g%28z%29%3D%20%5Cfrac%201%20%7B1%2Be%5E%7B-z%7D%7D%0A&height=32&width=89)

这个函数叫做逻辑函数 （Logistic function） ，或者也叫双弯曲S型函数（sigmoid function）。下图是 #card=math&code=g%28z%29&height=16&width=23) 的函数图像：

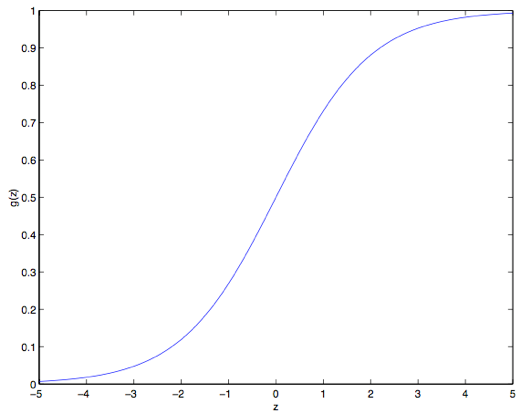
注意到没有，当 的时候 #card=math&code=g%28z%29&height=16&width=23) 趋向于，而当 时#card=math&code=g%28z%29&height=16&width=23) 趋向于。此外，这里的这个 #card=math&code=g%28z%29&height=16&width=23) ，也就是 #card=math&code=h%28x%29&height=16&width=25)，是一直在 和 之间波动的。然后咱们依然像最开始那样来设置 ，这样就有了：

现在咱们就把 作为选定的函数了。当然其他的从到之间光滑递增的函数也可以使用，不过后面我们会了解到选择 的一些原因（到时候我们讲广义线性模型 GLMs，那时候还会讲生成学习算法，generative learning algorithms），对这个逻辑函数的选择是很自然的。再继续深入之前，下面是要讲解的关于这个 S 型函数的导数，也就是 的一些性质：

%20%26%20%3D%20%5Cfrac%20d%7Bdz%7D%5Cfrac%201%7B1%2Be%5E%7B-z%7D%7D%5C%5C%0A%26%20%3D%20%5Cfrac%20%201%7B(1%2Be%5E%7B-z%7D)%5E2%7D(e%5E%7B-z%7D)%5C%5C%0A%26%20%3D%20%5Cfrac%20%201%7B(1%2Be%5E%7B-z%7D)%7D%20%5Ccdot%20(1-%20%5Cfrac%201%7B(1%2Be%5E%7B-z%7D)%7D)%5C%5C%0A%26%20%3D%20g(z)(1-g(z))%5C%5C%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0Ag%27%28z%29%20%26%20%3D%20%5Cfrac%20d%7Bdz%7D%5Cfrac%201%7B1%2Be%5E%7B-z%7D%7D%5C%5C%0A%26%20%3D%20%5Cfrac%20%201%7B%281%2Be%5E%7B-z%7D%29%5E2%7D%28e%5E%7B-z%7D%29%5C%5C%0A%26%20%3D%20%5Cfrac%20%201%7B%281%2Be%5E%7B-z%7D%29%7D%20%5Ccdot%20%281-%20%5Cfrac%201%7B%281%2Be%5E%7B-z%7D%29%7D%29%5C%5C%0A%26%20%3D%20g%28z%29%281-g%28z%29%29%5C%5C%0A%5Cend%7Baligned%7D%0A&height=123&width=210)

那么，给定了逻辑回归模型了，咱们怎么去拟合一个合适的 呢？我们之前已经看到了在一系列假设的前提下，最小二乘法回归可以通过最大似然估计来推出，那么接下来就给我们的这个分类模型做一系列的统计学假设，然后用最大似然法来拟合参数吧。

首先假设：

%26%3Dh%7B%5Ctheta%7D(x)%5C%5C%0AP(y%3D0%7Cx%3B%5Ctheta)%26%3D1-%20h%7B%5Ctheta%7D(x)%5C%5C%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AP%28y%3D1%7Cx%3B%5Ctheta%29%26%3Dh%7B%5Ctheta%7D%28x%29%5C%5C%0AP%28y%3D0%7Cx%3B%5Ctheta%29%26%3D1-%20h%7B%5Ctheta%7D%28x%29%5C%5C%0A%5Cend%7Baligned%7D%0A&height=36&width=153)

更简洁的写法是：

%3D(h%5Ctheta%20(x))%5Ey(1-%20h%5Ctheta%20(x))%5E%7B1-y%7D%0A#card=math&code=p%28y%7Cx%3B%5Ctheta%29%3D%28h%5Ctheta%20%28x%29%29%5Ey%281-%20h%5Ctheta%20%28x%29%29%5E%7B1-y%7D%0A&height=18&width=199)

假设 个训练样本都是各自独立生成的，那么就可以按如下的方式来写参数的似然函数：

%20%26%3D%20p(%5Cvec%7By%7D%7C%20X%3B%20%5Ctheta)%5C%5C%0A%26%3D%20%5Cprod%5Em%7Bi%3D1%7D%20%20p(y%5E%7B(i)%7D%7C%20x%5E%7B(i)%7D%3B%20%5Ctheta)%5C%5C%0A%26%3D%20%5Cprod%5Em%7Bi%3D1%7D%20(h%5Ctheta%20(x%5E%7B(i)%7D))%5E%7By%5E%7B(i)%7D%7D(1-h%5Ctheta%20(x%5E%7B(i)%7D))%5E%7B1-y%5E%7B(i)%7D%7D%20%5C%5C%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AL%28%5Ctheta%29%20%26%3D%20p%28%5Cvec%7By%7D%7C%20X%3B%20%5Ctheta%29%5C%5C%0A%26%3D%20%5Cprod%5Em%7Bi%3D1%7D%20%20p%28y%5E%7B%28i%29%7D%7C%20x%5E%7B%28i%29%7D%3B%20%5Ctheta%29%5C%5C%0A%26%3D%20%5Cprod%5Em%7Bi%3D1%7D%20%28h%5Ctheta%20%28x%5E%7B%28i%29%7D%29%29%5E%7By%5E%7B%28i%29%7D%7D%281-h%5Ctheta%20%28x%5E%7B%28i%29%7D%29%29%5E%7B1-y%5E%7B%28i%29%7D%7D%20%5C%5C%0A%5Cend%7Baligned%7D%0A&height=100&width=242)

然后还是跟之前一样，取个对数就更容易计算最大值：

%20%26%3D%5Clog%20L(%5Ctheta)%20%5C%5C%0A%26%3D%20%5Csum%5Em%7Bi%3D1%7D%20y%5E%7B(i)%7D%20%5Clog%20h(x%5E%7B(i)%7D)%2B(1-y%5E%7B(i)%7D)%5Clog%20(1-h(x%5E%7B(i)%7D))%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0Al%28%5Ctheta%29%20%26%3D%5Clog%20L%28%5Ctheta%29%20%5C%5C%0A%26%3D%20%5Csum%5Em%7Bi%3D1%7D%20y%5E%7B%28i%29%7D%20%5Clog%20h%28x%5E%7B%28i%29%7D%29%2B%281-y%5E%7B%28i%29%7D%29%5Clog%20%281-h%28x%5E%7B%28i%29%7D%29%29%0A%5Cend%7Baligned%7D%0A&height=59&width=305)

怎么让似然函数最大？就跟之前咱们在线性回归的时候用了求导数的方法类似，咱们这次就是用梯度上升法（gradient ascent）。还是写成向量的形式，然后进行更新，也就是 。 (注意更新方程中用的是加号而不是减号，因为我们现在是在找一个函数的最大值，而不是找最小值了。) 还是先从只有一组训练样本#card=math&code=%28x%2Cy%29&height=16&width=31) 来开始，然后求导数来推出随机梯度上升规则：

%20%26%3D(y%5Cfrac%20%201%20%7Bg(%5Ctheta%20%5ET%20x)%7D%20%20-%20(1-y)%5Cfrac%20%201%20%7B1-%20g(%5Ctheta%20%5ET%20x)%7D%20%20%20)%5Cfrac%20%20%7B%5Cpartial%7D%7B%5Cpartial%20%5Cthetaj%7Dg(%5Ctheta%20%5ETx)%20%5C%5C%0A%26%3D%20(y%5Cfrac%20%201%20%7Bg(%5Ctheta%20%5ET%20x)%7D%20%20-%20(1-y)%5Cfrac%20%201%20%7B1-%20g(%5Ctheta%20%5ET%20x)%7D%20%20%20)%20%20g(%5Ctheta%5ETx)(1-g(%5Ctheta%5ETx))%20%5Cfrac%20%20%7B%5Cpartial%7D%7B%5Cpartial%20%5Ctheta_j%7D%5Ctheta%20%5ETx%20%5C%5C%0A%26%3D%20(y(1-g(%5Ctheta%5ETx)%20)%20-(1-y)%20g(%5Ctheta%5ETx))%20x_j%5C%5C%0A%26%3D%20(y-h%5Ctheta(x))xj%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Cfrac%20%20%7B%5Cpartial%7D%7B%5Cpartial%20%5Ctheta_j%7D%20l%28%5Ctheta%29%20%26%3D%28y%5Cfrac%20%201%20%7Bg%28%5Ctheta%20%5ET%20x%29%7D%20%20-%20%281-y%29%5Cfrac%20%201%20%7B1-%20g%28%5Ctheta%20%5ET%20x%29%7D%20%20%20%29%5Cfrac%20%20%7B%5Cpartial%7D%7B%5Cpartial%20%5Ctheta_j%7Dg%28%5Ctheta%20%5ETx%29%20%5C%5C%0A%26%3D%20%28y%5Cfrac%20%201%20%7Bg%28%5Ctheta%20%5ET%20x%29%7D%20%20-%20%281-y%29%5Cfrac%20%201%20%7B1-%20g%28%5Ctheta%20%5ET%20x%29%7D%20%20%20%29%20%20g%28%5Ctheta%5ETx%29%281-g%28%5Ctheta%5ETx%29%29%20%5Cfrac%20%20%7B%5Cpartial%7D%7B%5Cpartial%20%5Ctheta_j%7D%5Ctheta%20%5ETx%20%5C%5C%0A%26%3D%20%28y%281-g%28%5Ctheta%5ETx%29%20%29%20-%281-y%29%20g%28%5Ctheta%5ETx%29%29%20x_j%5C%5C%0A%26%3D%20%28y-h%5Ctheta%28x%29%29x_j%0A%5Cend%7Baligned%7D%0A&height=111&width=412)

上面的式子里，我们用到了对函数求导的定理 。然后就得到了随机梯度上升规则：

%7D-h%5Ctheta%20(x%5E%7B(i)%7D))x_j%5E%7B(i)%7D%0A#card=math&code=%5Ctheta_j%20%3A%3D%20%5Ctheta_j%20%2B%20%5Calpha%20%28y%5E%7B%28i%29%7D-h%5Ctheta%20%28x%5E%7B%28i%29%7D%29%29x_j%5E%7B%28i%29%7D%0A&height=23&width=180)

如果跟之前的 LMS 更新规则相对比，就能发现看上去挺相似的；不过这并不是同一个算法，因为这里的%7D)#card=math&code=h_%5Ctheta%28x%5E%7B%28i%29%7D%29&height=19&width=44)现在定义成了一个 %7D#card=math&code=%5Ctheta%5ETx%5E%7B%28i%29%7D&height=16&width=34) 的非线性函数。尽管如此，我们面对不同的学习问题使用了不同的算法，却得到了看上去一样的更新规则，这个还是有点让人吃惊。这是一个巧合么，还是背后有更深层次的原因呢？在我们学到了 GLM 广义线性模型的时候就会得到答案了。（另外也可以看一下 习题集1 里面 Q3 的附加题。）

2.2 题外话: 感知器学习算法（The perceptron learning algorithm）

现在咱们来岔开一下话题，简要地聊一个算法，这个算法的历史很有趣，并且之后在我们讲学习理论的时候还要讲到它。设想一下，对逻辑回归方法修改一下，“强迫”它输出的值要么是 要么是 。要实现这个目的，很自然就应该把函数 的定义修改一下，改成一个阈值函数（threshold function）：

%3D%20%5Cbegin%7Bcases%7D%201%20%26%20%20if%5Cquad%20z%20%5Cgeq%200%20%20%5C%5C%0A0%20%26%20%20if%5Cquad%20z%20%3C%200%20%20%5Cend%7Bcases%7D%0A#card=math&code=g%28z%29%3D%20%5Cbegin%7Bcases%7D%201%20%26%20%20if%5Cquad%20z%20%5Cgeq%200%20%20%5C%5C%0A0%20%26%20%20if%5Cquad%20z%20%3C%200%20%20%5Cend%7Bcases%7D%0A&height=36&width=133)

如果我们还像之前一样令 %20%3D%20g(%5Ctheta%5ET%20x)#card=math&code=h_%5Ctheta%28x%29%20%3D%20g%28%5Ctheta%5ET%20x%29&height=18&width=89)，但用刚刚上面的阈值函数作为 的定义，然后如果我们用了下面的更新规则：

%7D-h%5Ctheta%20(x%5E%7B(i)%7D))x_j%5E%7B(i)%7D%0A#card=math&code=%5Ctheta_j%20%3A%3D%20%5Ctheta_j%20%2B%5Calpha%28y%5E%7B%28i%29%7D-h%5Ctheta%20%28x%5E%7B%28i%29%7D%29%29x_j%5E%7B%28i%29%7D%0A&height=23&width=180)

这样我们就得到了感知器学习算法。

在 1960 年代，这个“感知器（perceptron）”被认为是对大脑中单个神经元工作方法的一个粗略建模。鉴于这个算法的简单程度，这个算法也是我们后续在本课程中讲学习理论的时候的起点。但一定要注意，虽然这个感知器学习算法可能看上去表面上跟我们之前讲的其他算法挺相似，但实际上这是一个和逻辑回归以及最小二乘线性回归等算法在种类上都完全不同的算法；尤其重要的是，很难对感知器的预测赋予有意义的概率解释，也很难作为一种最大似然估计算法来推出感知器学习算法。

2.3 让#card=math&code=l%28%5Ctheta%29&height=16&width=20) 取最大值的另外一个算法

再回到用 S 型函数 #card=math&code=g%28z%29&height=16&width=23) 来进行逻辑回归的情况，咱们来讲一个让 #card=math&code=l%28%5Ctheta%29&height=16&width=20) 取最大值的另一个算法。

开始之前，咱们先想一下求一个方程零点的牛顿法。假如我们有一个从实数到实数的函数 ，然后要找到一个 ，来满足 %3D0#card=math&code=f%28%5Ctheta%29%3D0&height=16&width=49)，其中 是一个实数。牛顿法就是对 进行如下的更新：

%7D%7Bf’(%5Ctheta)%7D%0A#card=math&code=%5Ctheta%20%3A%3D%20%5Ctheta%20-%20%5Cfrac%20%7Bf%28%5Ctheta%29%7D%7Bf%27%28%5Ctheta%29%7D%0A&height=37&width=84)

这个方法可以通过一个很自然的解释，我们可以把它理解成用一个线性函数来对函数 进行逼近，这条直线是 的切线，而猜测值是 ，解的方法就是找到线性方程等于零的点，把这一个零点作为 设置给下一次猜测，然后以此类推。

下面是对牛顿法的图解：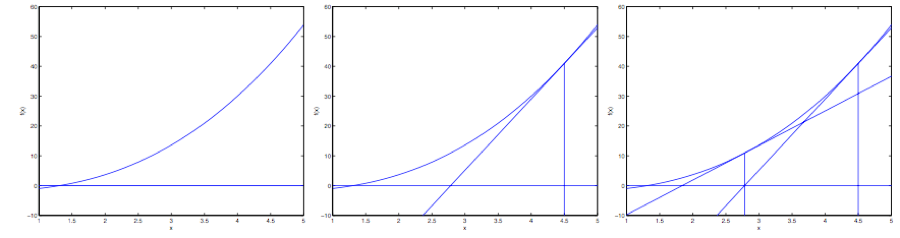

在最左边的图里面，可以看到函数 就是沿着 的一条直线。这时候是想要找一个 来让 %3D0#card=math&code=f%28%5Ctheta%29%3D0&height=16&width=49)。这时候发现这个 值大概在 左右。加入咱们猜测的初始值设定为 。牛顿法就是在 这个位置画一条切线（中间的图）。这样就给出了下一个 猜测值的位置，也就是这个切线的零点，大概是。最右面的图中的是再运行一次这个迭代产生的结果，这时候 大概是。就这样几次迭代之后，很快就能接近 。

牛顿法的给出的解决思路是让 %20%3D%200#card=math&code=f%28%5Ctheta%29%20%3D%200&height=16&width=49) 。如果咱们要用它来让函数 取得最大值能不能行呢？函数 的最大值的点应该对应着是它的导数#card=math&code=l%27%28%5Ctheta%29&height=17&width=24) 等于零的点。所以通过令%20%3D%20l’(%5Ctheta)#card=math&code=f%28%5Ctheta%29%20%3D%20l%27%28%5Ctheta%29&height=17&width=67)，咱们就可以同样用牛顿法来找到 的最大值，然后得到下面的更新规则：

%7D%7Bl’’(%5Ctheta)%7D%0A#card=math&code=%5Ctheta%20%3A%3D%20%5Ctheta%20-%20%5Cfrac%20%7Bl%27%28%5Ctheta%29%7D%7Bl%27%27%28%5Ctheta%29%7D%0A&height=37&width=83)

（扩展一下，额外再思考一下: 如果咱们要用牛顿法来求一个函数的最小值而不是最大值，该怎么修改？）译者注：试试法线的零点

最后，在咱们的逻辑回归背景中， 是一个有值的向量，所以我们要对牛顿法进行扩展来适应这个情况。牛顿法进行扩展到多维情况，也叫牛顿-拉普森法（Newton-Raphson method），如下所示：

%0A#card=math&code=%5Ctheta%20%3A%3D%20%5Ctheta%20-%20H%5E%7B-1%7D%5Cnabla_%5Ctheta%20l%28%5Ctheta%29%0A&height=18&width=115)

上面这个式子中的 #card=math&code=%5Cnabla_%5Ctheta%20l%28%5Ctheta%29&height=16&width=37)和之前的样例中的类似，是关于 的 #card=math&code=l%28%5Ctheta%29&height=16&width=20) 的偏导数向量；而 是一个 矩阵 ,实际上如果包含截距项的话，应该是, %5Ctimes%20(n%20%2B%201)#card=math&code=%28n%20%2B%201%29%5Ctimes%20%28n%20%2B%201%29&height=16&width=100)，也叫做 Hessian, 其详细定义是：

%7D%7B%5Cpartial%20%5Cthetai%20%5Cpartial%20%5Ctheta_j%7D%0A#card=math&code=H%7Bij%7D%3D%20%5Cfrac%20%7B%5Cpartial%5E2%20l%28%5Ctheta%29%7D%7B%5Cpartial%20%5Ctheta_i%20%5Cpartial%20%5Ctheta_j%7D%0A&height=38&width=81)

牛顿法通常都能比（批量）梯度下降法收敛得更快，而且达到最小值所需要的迭代次数也低很多。然而，牛顿法中的单次迭代往往要比梯度下降法的单步耗费更多的性能开销，因为要查找和转换一个 的 Hessian 矩阵；不过只要这个 不是太大，牛顿法通常就还是更快一些。当用牛顿法来在逻辑回归中求似然函数#card=math&code=l%28%5Ctheta%29&height=16&width=20) 的最大值的时候，得到这一结果的方法也叫做Fisher评分（Fisher scoring）。