参数估计

导读

参数估计导读来自 Junyi Hou.

点估计就是用一个数据（data）的函数（通常称为估计统计量，estimator）来给出一个未知参数的估计值。

即使是固定的参数真值（虽然我们不知道这个值），由于数据的随机性，不同的数据代入这个函数往往会得出不同的估计值（estimation ）。所以我们往往在点估计的基础上包裹上一个邻域，即得到一个区间估计。

那么点估计周围的这个邻域的大小是怎么确定的呢？一个最直接的答案就是：确定一个百分比，p%，使得给定任意数据集，参数的估计值（estimation）落在这个邻域内的概率为p%。那么，确定邻域大小的问题就变成了确定参数估计量（estimator）的分布的问题了。

首先，如果我们假设总体服从正态分布。那么可以证明，统计量作为随机变量的函数，往往会服从从正态分布中推导出来的一系列分布（如 t 分布，chi-square分布和F分布），那么通过统计量（estimator）的分布，我们可以很轻松的得到所求邻域的大小。

但是，在日常生活中，数据并不一定服从正态分布的。如果总体不是正态分布的，那么估计统计量（estimator）很可能也不服从正态分布，t 分布，chi-square 分布和 F 分布这些我们已知的分布。如果我们不知道统计量的分布，就无法确定应该给这个点估计包裹一个多大的邻域。

于是我们退而求其次，由于在满足一定正则条件的情况下，很多数据的分布都会在数据量趋近于无穷的情况下趋近于正态分布。比如，中心极限定理（Central Limit Theorem，以下简称 CLT）说的是样本均值的极限分布为正态分布。而估计量一般可以表示成样本均值的函数（e.g. OLS，GMM）， 所以知道了样本均值的极限（正态）分布也就知道了这些估计量的极限分布。于是我们就可以计算区间估计中的置信区间了。

最后，如果正则条件不满足，CLT 无法适用。数据分布即使在数据量趋于无穷的情况下仍然不是正态分布，这时候，采用传统方法得到区间估计的办法就行不通了。需要采用更加先进的方法（比如 bootstrapping 寻找区间估计；比如彻底抛弃 parametric model 转用 semi- non-parametric model 等等）。

其实 CLT 不单单在找区间估计的时候用到。很多假设检验的问题都依赖于统计量（或者数据等）的分布是正态分布这一假设。所以如果假设统计量本身就是正态的，那么当然可以以这些统计量为基础进行假设检验。但是如果分布不是正态的，那很有可能就需要 CLT 来帮助（至少建立在极限状态下的正态性）证明假设检验（包括区间估计）的正当性：因为如果统计量不是正态的，那么得出来的东西根本对不上号，假设检验也就没啥大意义了。

点估计

矩估计

在统计学中，矩估计（英语：method of moments）是估计总体参数的方法。首先推导涉及感兴趣的参数的总体矩（即所考虑的随机变量的幂的期望值）的方程。然后取出一个样本并从这个样本估计总体矩。接着使用样本矩取代（未知的）总体矩，解出感兴趣的参数。从而得到那些参数的估计。矩估计是英国统计学家卡尔·皮尔逊于1894年提出的。

假设问题是要估计表征随机变量 的分布 的 个未知参数. 如果真实分布（”总体矩”）的前 阶矩可以表示成这些 的函数:

设取出一大小为 的样本，得到 。对于 , 令

为 j 阶样本矩，是 的估计。 的矩估计量记为 ，由这些方程的解（如果存在）定义：

极大似然估计

在统计学中，最大似然估计（英语：maximum likelihood estimation，缩写为MLE），也称极大似然估计、最大概似估计，是用来估计一个概率模型的参数的一种方法。

给定一个概率分布 D，已知其概率密度函数（连续分布）或概率质量函数（离散分布）为 ，以及一个分布参数 ，我们可以从这个分布中抽出一个具有 n 个值的采样 ，利用 计算出其似然函数：

若 D 是离散分布， 即是在参数为 时观测到这一采样的概率。若其是连续分布， 则为 联合分布的概率密度函数在观测值处的取值。一旦我们获得 ，我们就能求得一个关于 的估计。最大似然估计会寻找关于 的最可能的值（即，在所有可能的 取值中，寻找一个值使这个采样的“可能性”最大化）。从数学上来说，我们可以在 的所有可能取值中寻找一个值使得似然函数取到最大值。这个使可能性最大的 值即称为 的最大似然估计。由定义，最大似然估计是样本的函数。

估计量的评选标准

无偏性, 有效性, 相合性.

区间估计

基本思路

1. 如果已知总体分布为正态分布，那么从抽样分布一节我们知道，其某些样本统计量满足正态分布，卡方分布， 分布和 分布。
2. 知道样本统计量的分布对我们来说是非常有帮助的，即使在我们不知道分布参数的情况下。比如我们知道了总体 #card=math&code=X%5Csim%20N%5Cleft%28%20%5Cmu%20%2C%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%5Cright%29&height=24&width=104)，那么样本均值 #card=math&code=%5Cbar%20%7B%20X%20%7D%20%5Csim%20N%5Cleft%28%20%5Cmu%20%2C%5Cfrac%20%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%7B%20n%20%7D%20%20%5Cright%29&height=45&width=119)，如果我们知道 和 ，那么只有一个未知参数 不知道，这个 也是我们要估计的未知参数。
3. 由 原则我们知道，如果我们得到一个样本，并求出样本均值的观察值 ，那么 %20%5Capprox%2095%5C%25#card=math&code=P%5Cleft%28%20%5Cmu%20-2%5Cfrac%20%7B%20%5Csigma%20%20%7D%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%3C%5Cbar%20%7B%20%7B%20X%20%7D%7B%200%20%7D%20%7D%20%3C%5Cmu%20%2B2%5Cfrac%20%7B%20%5Csigma%20%20%7D%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%20%5Cright%29%20%5Capprox%2095%5C%25&height=47&width=298)，我们再将这个式子变形即可得 %20%5Capprox%2095%5C%25#card=math&code=P%5Cleft%28%20%5Cbar%20%7B%20%7B%20X%20%7D%7B%200%20%7D%20%7D%20-2%5Cfrac%20%7B%20%5Csigma%20%20%7D%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%3C%5Cmu%20%3C%5Cbar%20%7B%20%7B%20X%20%7D%7B%200%20%7D%20%7D%20%2B2%5Cfrac%20%7B%20%5Csigma%20%20%7D%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%20%5Cright%29%20%5Capprox%2095%5C%25&height=47&width=309)，这个式子的意思就是：我们要估计的未知参数μ在 #card=math&code=%5Cleft%28%20%5Cbar%20%7B%20%7B%20X%20%7D%7B%200%20%7D%20%7D%20-2%5Cfrac%20%7B%20%5Csigma%20%20%7D%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%2C%5Cbar%20%7B%20%7B%20X%20%7D_%7B%200%20%7D%20%7D%20%2B2%5Cfrac%20%7B%20%5Csigma%20%20%7D%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%20%5Cright%29&height=47&width=193) 这个区间内的概率约等于95%。
4. 3中的结论，我们可以换一种等价的说法或思考的角度，也就是说：如果我们要求未知参数的真值在某个区间内的概率为95%，那么这个区间就得是 #card=math&code=%5Cleft%28%20%5Cbar%20%7B%20%7B%20X%20%7D%7B%200%20%7D%20%7D%20-2%5Cfrac%20%7B%20%5Csigma%20%20%7D%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%2C%5Cbar%20%7B%20%7B%20X%20%7D%7B%200%20%7D%20%7D%20%2B2%5Cfrac%20%7B%20%5Csigma%20%20%7D%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%20%5Cright%29&height=47&width=193)。这个 95% 叫做置信水平 ，为弃真错误，得到的区间成为置信区间（Confidence interval），区间的上下限称为置信上限和置信下限。
5. 但是 原则毕竟有局限性，我们也不能每次估计时都要求是 95% 的置信水平，所以为了更精确地估计，我们需要知道置信水平和置信区间的具体关系。
6. 我们回到 3 中，当我们知道 #card=math&code=%5Cbar%20%7B%20X%20%7D%20%5Csim%20N%5Cleft%28%20%5Cmu%20%2C%5Cfrac%20%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%7B%20n%20%7D%20%20%5Cright%29&height=45&width=119)， 是一个统计量，我们可以进一步知道 #card=math&code=%5Cfrac%20%7B%20%5Cbar%20%7B%20X%20%7D%20-%5Cmu%20%20%7D%7B%20%7B%20%5Csigma%20%20%7D%2F%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%7D%20%5Csim%20N%5Cleft%28%200%2C1%20%5Cright%29&height=48&width=128)， 是一个我们构造的统计量 ，因为其分布是更加简单的单位正态分布，所以我们用它来分析。其概率密度图如下：

1. 那么当我们有了置信水平 以及 的定义，我们可以得到一个类似的等式：%20%3D1-%5Calpha#card=math&code=P%5Cleft%28%20-%7B%20z%20%7D%7B%20%7B%20%5Cfrac%20%7B%20%5Calpha%20%20%7D%7B%202%20%7D%20%20%7D%20%7D%3Cz%3C%7B%20z%20%7D%7B%20%7B%20%5Cfrac%20%7B%20%5Calpha%20%20%7D%7B%202%20%7D%20%20%7D%20%7D%20%5Cright%29%20%3D1-%5Calpha&height=35&width=206)，这个等式就将 和 联系起来，将 代入该式，并做等价变换可得 %20%3D1-%5Calpha#card=math&code=P%5Cleft%28%20%5Cbar%20%7B%20X%20%7D%20-%7B%20z%20%7D%7B%20%7B%20%5Cfrac%20%7B%20%5Calpha%20%20%7D%7B%202%20%7D%20%20%7D%20%7D%5Cfrac%20%7B%20%5Csigma%20%20%7D%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%3C%5Cmu%20%3C%5Cbar%20%7B%20X%20%7D%20%2B%7B%20z%20%7D%7B%20%7B%20%5Cfrac%20%7B%20%5Calpha%20%20%7D%7B%202%20%7D%20%20%7D%20%7D%5Cfrac%20%7B%20%5Csigma%20%20%7D%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%20%5Cright%29%20%3D1-%5Calpha&height=47&width=331)，这样在 ，和 都已知的情况下，用这四个量表示出了未知参数 的置信区间。
2. 整理思路，我们如果知道总体分布为正态分布，并且知道其标准差 和样本容量 ，当我们给出置信区间 情况下，利用得到的一个样本计算出其样本均值 ，我们通过构造统计量 结合其分布性质，就可以得到未知参数 的置信区间，也就是对 进行了区间估计：

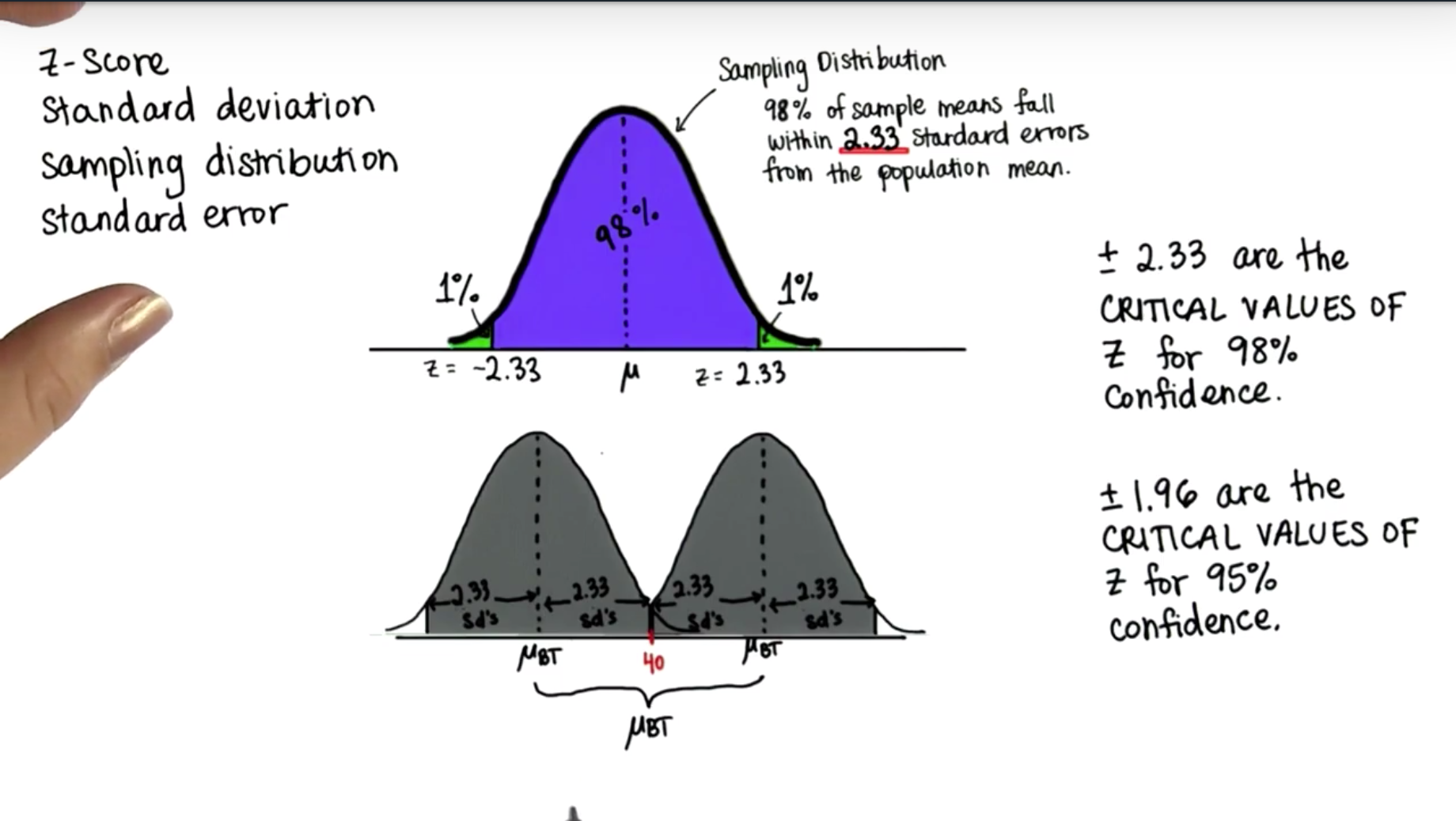
1. 以上是我们对特定总体情况的区间估计，这个特定情况是总体服从正态分布且已知方差，但是，实际中可能我们并不知道方差，或者我们知道均值想估计方差，亦或是均值和方差都不知道，甚至总体可能都不服从正态分布，这个时候我们就不能通过样本均值这个统计量来进行参数估计了，就需要通过其他一些统计量，比如 等等。但我们有区间估计与假设检验表，通过这个表我们可以快速判断自己应该使用哪个统计量以及估计或统计方法，这是十分方便的。
2. 样本容量越大，置信区间越窄；置信度越高，置信区间越宽。