样本及抽样分布

统计学概述

在概率论中，我们多研究的随机变量，它的分布都是假设已知的。如果你已经知道了随机变量X是的分布和参数，你去推导它的期望、方差等数字特征，去推导它其他一些性质，去推导X的平方是什么分布，或推导和另一个随机变量Y相加又是什么分布。这些工作属于概率论范畴。

但在数理统计中，我们研究的随机变量，它的分布是未知的，或者是某些参数不知道，人们通过对所研究的随机变量进行重复独立的观察，得到许多观察值，对这些数据进行分析，从而对所研究的随机变量的分布做出种种推断。比如，实际工作中有个随机变量Z，你不知道是什么分布，你看到了一些试验值，觉得Z可能是正态分布，于是你假设Z是正态分布，你用试验数据，推断出它的均值可能是1，方差可能是4，然后做假设检验，看看这一结论在多大程度上可靠，如果认为可靠，用这个结论来做分析，或者预测将要进行的试验结果。这叫统计。

概率论是统计推断的基础，在给定数据生成过程下观测、研究数据的性质，是推理；而统计推断则根据观测的数据，反向思考其数据生成过程。预测、分类、聚类、估计等，都是统计推断的特殊形式，强调对于数据生成过程的研究，是归纳。

抽样：总体与样本

总体

总体，是指由许多有某种共同性质的事物组成的集合，会在此集合中选出样本进行统计推断，选取样本的方式可能会用乱数或是其他抽样方式。

例如要针对所有乌鸦的共有特性进行研究，总体是目前存在、以前曾经存在或是未来可能存在的所有乌鸦。但是，因为时间的限制、地域可取得性的限制、以及研究者的有限资源等，不可能观测总体中的每一个，因此研究者会从总体中产生样本，再由样本的特性去了解总体的特性。

产生样本的目的之一就是为了要知道总体的特性，包括

• 总体均值：
• 总体标准差：%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D#card=math&code=%5Csigma%20%3D%5Csqrt%20%7B%20%5Cfrac%20%7B%201%20%7D%7B%20N%20%7D%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20N%20%7D%7B%20%7B%20%5Cleft%28%20%7B%20x%20%7D%7B%20i%20%7D-%5Cmu%20%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D&height=57&width=167)

样本

研究中，从总体中抽取（观察或调查）一部分的个体称为样本。

样本容量

样本容量是指一个样本中所包含的单位数，一般用n表示，它是抽样推断中非常重要的概念。样本容量的大小与推断估计的准确性有着直接的联系，即在总体既定的情况下，样本容量越大其统计估计量的代表性误差就越小，反之,样本容量越小其估计误差也就越大。

最常用的样本统计量——样本均值

根据样本构造的不含未知参数的函数为统计量，样本均值是一个统计量。我们可以用样本均值描述一个样本，多个样本则会有多个样本均值。

描述统计

直方图和箱线图

分位

Q1：四分位

Q3：四分之三分位

IQR：四分位差

1. 几乎 50% 的数据在 IQR 间。
2. IQR 受到数据集中每一个值的影响。
3. IQR 不受异常值的影响。
4. 均值不一定在IQR中。

异常值Outlier

箱线图Boxplot

集中趋势

均值Mean

当数据中出现异常值时，均值无法描述分布中心；

中位数Medium

众数也很难描述分布中心；

众数Mode

中位数不会考虑到所有的数据，对异常值的鲁棒性更好。在处理高偏斜分布时，中位数通常能够最好地反映出集中趋势。

正偏斜分布与负斜分布

正斜分布靠左：

负斜分布靠右：

鲁棒性Robust

即使偏离了基准也不会受太大的影响。

离散程度

方法

找出任意两个值之间差的平均值：数值过多

找出每个值与最大值或最小值之间差的平均值：容易受异常值干扰

找出每个值与数据集均值之间差的平均值：适合

概念

离均差：

平均偏差：

平均绝对偏差：

（总体）方差(平均平方偏差)：%20%20%7D%5E%7B%202%20%7D%20%7D%7B%20n%20%7D%20%20%7D%20%3DE%7B%20%5Cleft(%20X-EX%20%5Cright)%20%20%7D%5E%7B%202%20%7D%3DE%7B%20X%20%7D%5E%7B%202%20%7D-%7B%20%5Cleft(%20EX%20%5Cright)%20%20%7D%5E%7B%202%20%7D#card=math&code=DX%3D%5Csum%20%7B%20%5Cfrac%20%7B%20%7B%20%5Cleft%28%20%7B%20x%20%7D_%7B%20i%20%7D-%5Cbar%20%7B%20x%20%7D%20%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%7B%20n%20%7D%20%20%7D%20%3DE%7B%20%5Cleft%28%20X-EX%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%3DE%7B%20X%20%7D%5E%7B%202%20%7D-%7B%20%5Cleft%28%20EX%20%5Cright%29%20%20%7D%5E%7B%202%20%7D&height=43&width=394)

（总体）标准差：

贝塞尔校正

比如在高斯分布（正态分布）中，我们抽取一部分的样本，用样本的方差来估计总体的方差。由于样本主要是落在 中心值附近，那么样本方差一定小于总体的方差（因为高斯分布的边沿抽取的数据很少）。为了能弥补这方面的缺陷，那么我们把公式的 改为 ,以此来提高方差的数值。这种方法叫做贝塞尔校正系数。

当我们用小样本数据的标准差去估计总体的标准差的时候采用 ，但是这个小样本数据的实际标准差还是用 的那个公式 的，不要混淆了数据的实际标准差。

无偏性证明

对于一个随机变量 进行 次抽样，获得样本 ，那么样本均值：

有偏的样本方差为:

%20%7D%5E%7B%202%20%7D%20%7D%20%3D%5Cfrac%20%7B%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20x%20%7D%7B%20i%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%7B%20n%20%7D%20-%5Cfrac%20%7B%20%7B%20%5Cleft(%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20x%20%7D%7B%20i%20%7D%20%7D%20%20%5Cright)%20%20%7D%5E%7B%202%20%7D%20%7D%7B%20%7B%20n%20%7D%5E%7B%202%20%7D%20%7D#card=math&code=%7B%20s%20%7D%7B%20n%20%7D%5E%7B%202%20%7D%3D%5Cfrac%20%7B%201%20%7D%7B%20n%20%7D%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20%28%7B%20x%20%7D%7B%20i%20%7D-%5Cbar%20%7B%20x%20%7D%20%29%20%7D%5E%7B%202%20%7D%20%7D%20%3D%5Cfrac%20%7B%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20x%20%7D%7B%20i%20%7D%5E%7B%202%20%7D%20%7D%20%20%7D%7B%20n%20%7D%20-%5Cfrac%20%7B%20%7B%20%5Cleft%28%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20x%20%7D_%7B%20i%20%7D%20%7D%20%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%7B%20%7B%20n%20%7D%5E%7B%202%20%7D%20%7D&height=54&width=343)

无偏的样本方差为：

%20%7D%5E%7B%202%20%7D%20%7D%20%3D%5Cleft(%20%5Cfrac%20%7B%20n%20%7D%7B%20n-1%20%7D%20%20%5Cright)%20%7B%20s%20%7D%7B%20n%20%7D%5E%7B%202%20%7D#card=math&code=%7B%20s%20%7D%5E%7B%202%20%7D%3D%5Cfrac%20%7B%201%20%7D%7B%20n-1%20%7D%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20%28%7B%20x%20%7D%7B%20i%20%7D-%5Cbar%20%7B%20x%20%7D%20%29%20%7D%5E%7B%202%20%7D%20%7D%20%3D%5Cleft%28%20%5Cfrac%20%7B%20n%20%7D%7B%20n-1%20%7D%20%20%5Cright%29%20%7B%20s%20%7D%7B%20n%20%7D%5E%7B%202%20%7D&height=49&width=291)

为了证明 的无偏性， 我们拿出样本方差种的一部分来进行单独分析,

%20%20%7D%5E%7B%202%20%7D%20%7D%20%5C%5C%20%3D%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%5Cleft(%20%7B%20x%20%7D%7B%20i%20%7D%5E%7B%202%20%7D-2%7B%20x%20%7D%7B%20i%20%7D%5Cbar%20%7B%20x%20%7D%20%2B%7B%20%5Cbar%20%7B%20x%20%7D%20%20%7D%5E%7B%202%20%7D%20%5Cright)%20%20%7D%20%5C%5C%20%3D%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20x%20%7D%7B%20i%20%7D%5E%7B%202%20%7D%20%7D%20-2%5Cbar%20%7B%20x%20%7D%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20x%20%7D%7B%20i%20%7D%20%7D%20%2B%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20%5Cbar%20%7B%20x%20%7D%20%20%7D%5E%7B%202%20%7D%20%7D%20%5C%5C%20%3D%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20x%20%7D%7B%20i%20%7D%5E%7B%202%20%7D%20%7D%20-2n%7B%20%5Cbar%20%7B%20x%20%7D%20%20%7D%5E%7B%202%20%7D%2Bn%7B%20%5Cbar%20%7B%20x%20%7D%20%20%7D%5E%7B%202%20%7D%5C%5C%20%3D%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20x%20%7D%7B%20i%20%7D%5E%7B%202%20%7D%20%7D%20-n%7B%20%5Cbar%20%7B%20x%20%7D%20%20%7D%5E%7B%202%20%7D#card=math&code=%5Cquad%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20%5Cleft%28%20%7B%20x%20%7D%7B%20i%20%7D-%5Cbar%20%7B%20x%20%7D%20%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%20%5C%5C%20%3D%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%5Cleft%28%20%7B%20x%20%7D%7B%20i%20%7D%5E%7B%202%20%7D-2%7B%20x%20%7D%7B%20i%20%7D%5Cbar%20%7B%20x%20%7D%20%2B%7B%20%5Cbar%20%7B%20x%20%7D%20%20%7D%5E%7B%202%20%7D%20%5Cright%29%20%20%7D%20%5C%5C%20%3D%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20x%20%7D%7B%20i%20%7D%5E%7B%202%20%7D%20%7D%20-2%5Cbar%20%7B%20x%20%7D%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20x%20%7D%7B%20i%20%7D%20%7D%20%2B%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20%5Cbar%20%7B%20x%20%7D%20%20%7D%5E%7B%202%20%7D%20%7D%20%5C%5C%20%3D%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20x%20%7D%7B%20i%20%7D%5E%7B%202%20%7D%20%7D%20-2n%7B%20%5Cbar%20%7B%20x%20%7D%20%20%7D%5E%7B%202%20%7D%2Bn%7B%20%5Cbar%20%7B%20x%20%7D%20%20%7D%5E%7B%202%20%7D%5C%5C%20%3D%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20x%20%7D%7B%20i%20%7D%5E%7B%202%20%7D%20%7D%20-n%7B%20%5Cbar%20%7B%20x%20%7D%20%20%7D%5E%7B%202%20%7D&height=264&width=724)

同理，我们有

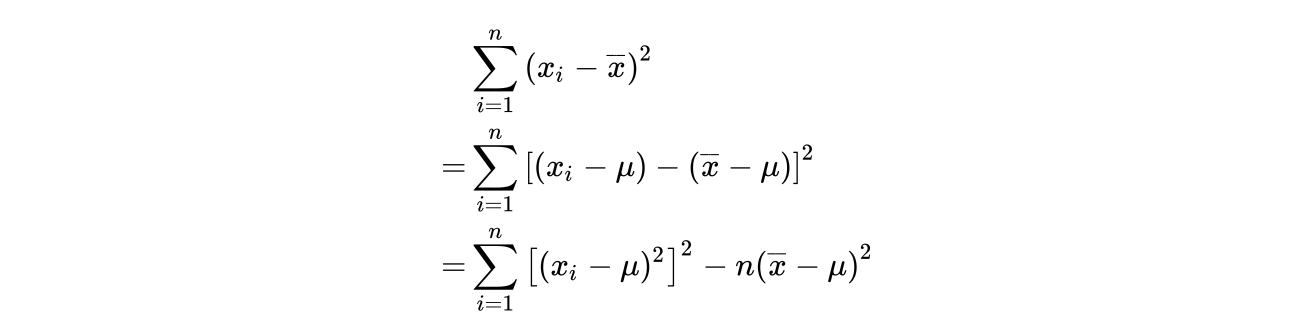
对上式两侧取期望，我们有

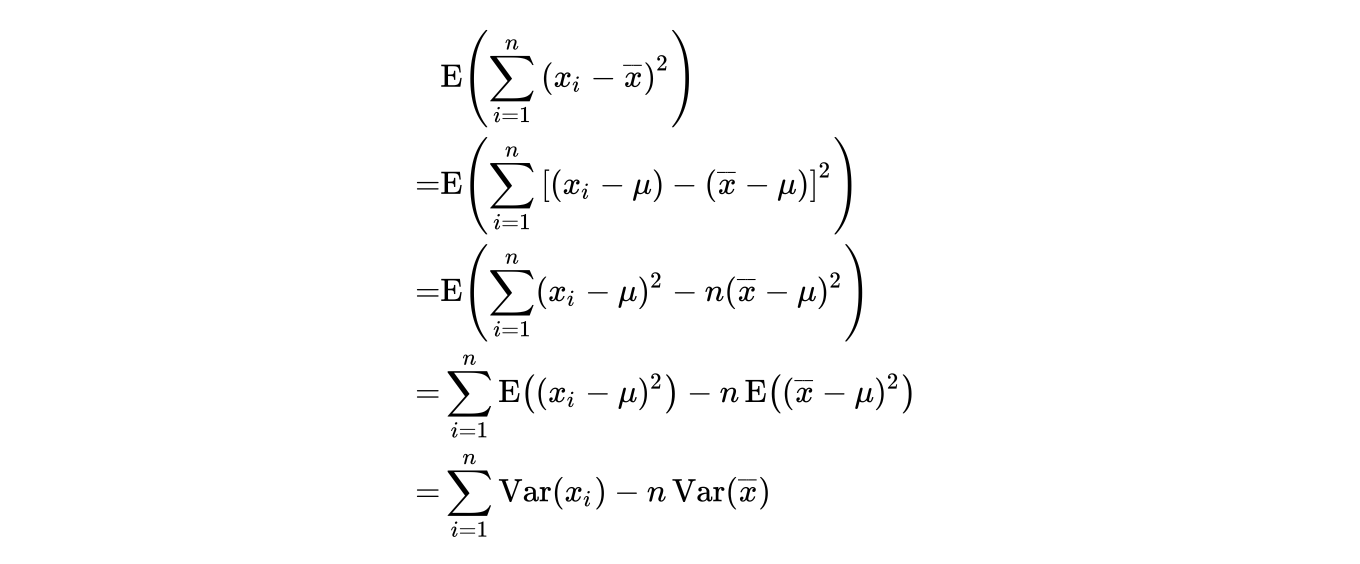
因为 ，于是我们有 %7D%20%3D%20%5Cfrac%7B1%7D%7Bn%7D%5Coperatorname%7BVar%7D%7B%7Bx%7D%7D%20%5Cend%7Balign*%7D#card=math&code=%5Cbegin%7Balign%2A%7D%20%5Coperatorname%7BVar%7D%7B%28%5Coverline%20%7Bx%7D%29%7D%20%3D%20%5Cfrac%7B1%7D%7Bn%7D%5Coperatorname%7BVar%7D%7B%7Bx%7D%7D%20%5Cend%7Balign%2A%7D&height=37&width=138)

因此

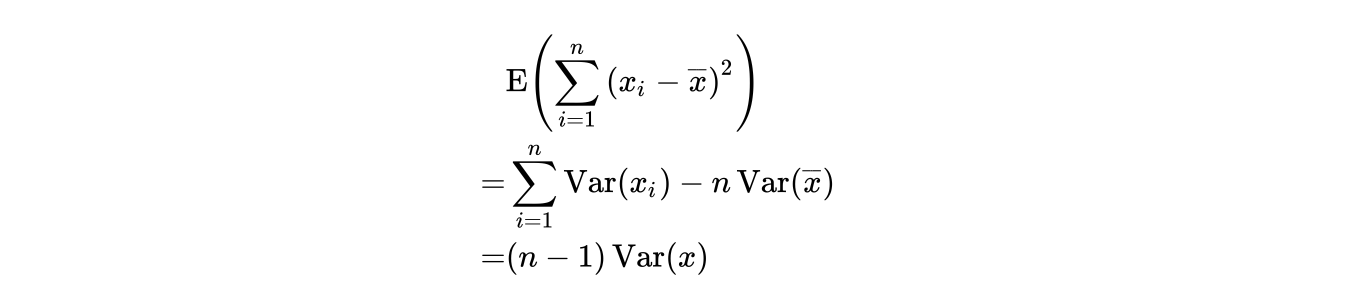
最后，我们有

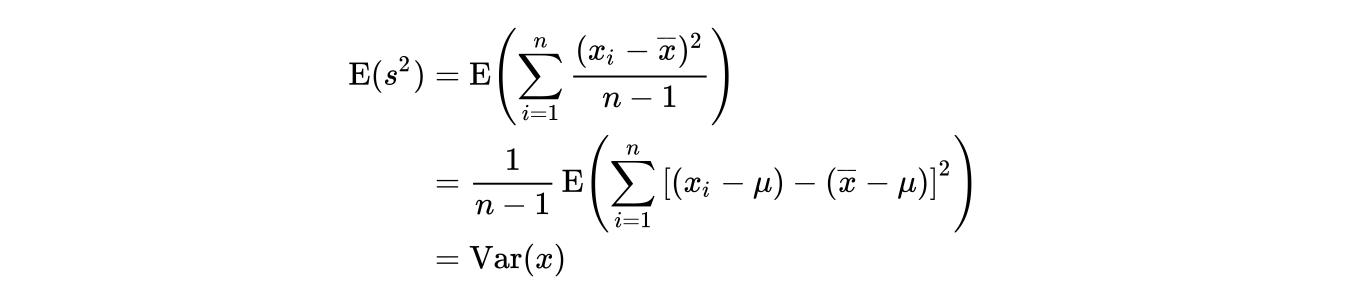
可见 是对 #card=math&code=Var%5Cleft%28%20X%20%5Cright%29&height=20&width=59) 的无偏估计。

3σ 原则

数值分布在 #card=math&code=%28%CE%BC-%CF%83%2C%CE%BC%2B%CF%83%29&height=20&width=101) 中的概率为 0.6827。

数值分布在 #card=math&code=%28%CE%BC-2%CF%83%2C%CE%BC%2B2%CF%83%29&height=20&width=118) 中的概率为 0.9545。

数值分布在 #card=math&code=%28%CE%BC-3%CF%83%2C%CE%BC%2B3%CF%83%29&height=20&width=118) 中的概率为 0.9973。

归一化：标准正态分布

样本均值的频数直方图的数字不能直接看出比例排名，所以引入频率直方图，但直方图固有弊端在于会缺少部分信息，所以需要缩小组距以增加信息，但过小又没有了直方图意义，所以引入概率分布图——标准正态分布。

Z 值：标准差数量

公式

含义

无论值是多少，我们都可以将其转换为与均值的标准差。通过将正态分布中的值转换为 ，就可以知道小于或大于该值得百分比。

例如某个值与平均值相差 1 个标准偏差 ，则无论是哪种正态分布，我们都知道大约 80% 的值 < 该值。

标准正态分布

我们可以将任何正态分布转化为标准正态分布，通过 值进行分析，再按照任何方式扩展。

Z 值表

链接。

抽样分布

样本统计量

根据样本构造的不含未知参数的函数为统计量。

样本均值

样本方差

%20%20%7D%5E%7B%202%20%7D%20%7D%20%7D%20%3D%5Cfrac%20%7B%201%20%7D%7B%20n-1%20%7D%20%5Cleft(%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20X%20%7D%7B%20i%20%7D%5E%7B%202%20%7D%20%7D%20-n%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%5E%7B%202%20%7D%20%5Cright)#card=math&code=%7B%20S%20%7D%5E%7B%202%20%7D%3D%5Cfrac%20%7B%201%20%7D%7B%20n-1%20%7D%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20%7B%20%5Cleft%28%20%7B%20X%20%7D%7B%20i%20%7D-%5Cbar%20%7B%20X%20%7D%20%20%5Cright%29%20%20%7D%5E%7B%202%20%7D%20%7D%20%7D%20%3D%5Cfrac%20%7B%201%20%7D%7B%20n-1%20%7D%20%5Cleft%28%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20X%20%7D%7B%20i%20%7D%5E%7B%202%20%7D%20%7D%20-n%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%5E%7B%202%20%7D%20%5Cright%29&height=54&width=390)

样本标准差

%20%20%7D#card=math&code=S%3D%5Csqrt%20%7B%20%7B%20S%20%7D%5E%7B%202%20%7D%20%7D%20%3D%5Csqrt%20%7B%20%5Cfrac%20%7B%201%20%7D%7B%20n-1%20%7D%20%5Cleft%28%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20X%20%7D%7B%20i%20%7D%5E%7B%202%20%7D%20%7D%20-n%7B%20%5Cbar%20%7B%20X%20%7D%20%20%7D%5E%7B%202%20%7D%20%5Cright%29%20%20%7D&height=59&width=282)

样本K阶(原点)矩

样本K阶中心矩

%20%20%7D%5E%7B%20k%20%7D%20%7D%20%2C%5Cquad%20k%3D1%2C2%2C%E2%80%A6#card=math&code=%7B%20B%20%7D%7B%20k%20%7D%3D%5Cfrac%20%7B%201%20%7D%7B%20n%20%7D%20%5Csum%20%7B%20i%3D1%20%7D%5E%7B%20n%20%7D%7B%20%7B%20%5Cleft%28%20%7B%20X%20%7D_%7B%20i%20%7D-%5Cbar%20%7B%20X%20%7D%20%20%5Cright%29%20%20%7D%5E%7B%20k%20%7D%20%7D%20%2C%5Cquad%20k%3D1%2C2%2C%E2%80%A6&height=49&width=274)

抽样分布

在使用统计量进行统计推断时，需要知道统计量的分布，比如样本均值的分布。

统计量的分布，叫做抽样分布。总体分布函数已知时，样本分布是确定的，但是：

1. 通常，我们是不知道总体分布的；
2. 要求出统计量的精确分布是困难的。

虽然总体不知道时，我们很难确定，解决这种问题需要学习非参数统计。然而，有两种情况是比较好研究的：

1. 对于正太总体分布，其常用的统计量的分布是可以推断出来的。
2. 对于一般总体分布，我们可以由大数定律和中心极限定理得到其样本均值统计量的期望、分布和方差等。

正态总体的常用统计量的分布

假设总体 #card=math&code=X%5Csim%20N%5Cleft%28%20%5Cmu%20%2C%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%5Cright%29&height=24&width=104)。

我们可能会用到各种各样的统计量，但归根结底是这些统计量满足四种典型的分布，即 （即正态分布）、、 和 分布，每一个分布对应一种检验方法，即 检验、检 验、 检验和 检验。

这些统计量大多都是一个样本或多个样本的样本均值 、样本方差 、总体均值 和总体方差 这些元素组成的，比如 等，但我们在选择时，一定要只有被检验一个参数不知道，所以，如果我们想用第一个统计量，那么除了 ，n这俩一定知道的参数之外，如果我们要检验 ，那么就必须知道总体标准差 。换句话说，如果我们知道总体标准差 ，那么我们就可以选择 这个统计量，并根据其满足的标准正态分布规律对总体均值 进行假设检验（或求置信区间）。

但是实际情况中，总体标准差 我们大多不知道，这个时候就不能使用 这个统计量了，而由于我们能求出样本标准差 ，那么就可以选择 这个统计量，这个统计量需要知道的关于总体的信息（参数）更少，但也服从 #card=math&code=t%28n-1%29&height=20&width=57) 分布。也就是只需要知道总体满足正态分布即可，而不需要知道其总体方差 ，就可以对总体均值 进行检验。

我们了解并学习这 4 种分布，是因为这 4 种分布，其分布函数和密度函数都能很好地进行量化，正态分布就是最好的例子，其他三种只是学习之前我们不常接触而已。

以下是对这四种分布的详细的介绍。

样本均值的正态分布

样本均值是最常用的统计量之一，一般用于 -检验，用以检验总体均值。

统计量：，或

统计量分布：#card=math&code=%5Cbar%20%7B%20X%20%7D%20%5Csim%20N%5Cleft%28%20%CE%BC%2C%5Cfrac%20%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%7B%20n%20%7D%20%20%5Cright%29&height=45&width=119)，或 #card=math&code=z%5Csim%20N%5Cleft%28%200%2C1%20%5Cright%29&height=20&width=85)。

卡方分布

定义

设 #card=math&code=X%5Csim%20N%5Cleft%28%200%20%2C1%20%5Cright%29&height=20&width=91)，则称统计量

服从自由度为 的 #card=math&code=%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft%28%20n%20%5Cright%29&height=23&width=84)，自由度指上式右端包含的独立变量的个数。

密度函数

%20%3D%5Cfrac%20%7B%201%20%7D%7B%20%7B%202%20%7D%5E%7B%20n%2F2%20%7D%5CGamma%20%5Cleft(%20n%2F2%20%5Cright)%20%20%7D%20%7B%20y%20%7D%5E%7B%20n%2F2-1%20%7D%7B%20e%20%7D%5E%7B%20-y%2F2%20%7D#card=math&code=%7B%20f%20%7D_%7B%20n%20%7D%5Cleft%28%20y%20%5Cright%29%20%3D%5Cfrac%20%7B%201%20%7D%7B%20%7B%202%20%7D%5E%7B%20n%2F2%20%7D%5CGamma%20%5Cleft%28%20n%2F2%20%5Cright%29%20%20%7D%20%7B%20y%20%7D%5E%7B%20n%2F2-1%20%7D%7B%20e%20%7D%5E%7B%20-y%2F2%20%7D&height=45&width=233)，其中 ；

当 时，%3D0%7D#card=math&code=%7B%5Cdisplaystyle%20f_%7Bk%7D%28x%29%3D0%7D&height=20&width=70)。这里 代表Gamma函数。

推导见书P139

图形

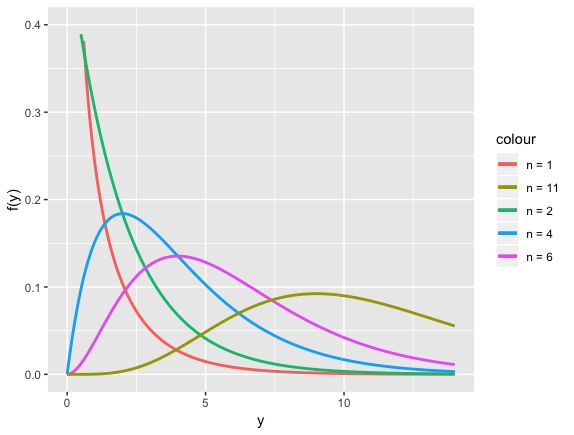
卡方分布的可加性

设 %20%2C%7B%20%5Cchi%20%20%7D%7B%202%20%7D%5E%7B%202%20%7D%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft(%20%7B%20n%20%7D%7B%202%20%7D%20%5Cright)#card=math&code=%7B%20%5Cchi%20%20%7D%7B%201%20%7D%5E%7B%202%20%7D%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft%28%20%7B%20n%20%7D%7B%201%20%7D%20%5Cright%29%20%2C%7B%20%5Cchi%20%20%7D%7B%202%20%7D%5E%7B%202%20%7D%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft%28%20%7B%20n%20%7D%7B%202%20%7D%20%5Cright%29&height=24&width=195)，并且 相互独立，则有 #card=math&code=%7B%20%5Cchi%20%20%7D%7B%201%20%7D%5E%7B%202%20%7D%2B%7B%20%5Cchi%20%20%7D%7B%202%20%7D%5E%7B%202%20%7D%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft%28%20%7B%20n%20%7D%7B%201%20%7D%2B%7B%20n%20%7D%7B%202%20%7D%20%5Cright%29&height=24&width=169)

卡方分布的数学期望和方差

#card=math&code=%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft%28%20%7B%20n%20%7D%20%5Cright%29&height=23&width=84)，则 %3Dn%2C%20D(%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D)%3D2n#card=math&code=E%28%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%29%3Dn%2C%20D%28%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%29%3D2n&height=23&width=170) 。

卡方分布上的分位点

对于给定的 ，满足条件：

%5C%7D%20%3D%5Cint%20%7B%20%7B%20%5Cchi%20%20%7D%7B%20%5Calpha%20%20%7D%5E%7B%202%20%7D(n)%20%7D%5E%7B%20%5Cinfty%20%20%7D%7B%20f(y)dy%3D%5Calpha%20%20%7D#card=math&code=P%5C%7B%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%3E%7B%20%5Cchi%20%20%7D%7B%20%5Calpha%20%20%7D%5E%7B%202%20%7D%28n%29%5C%7D%20%3D%5Cint%20%7B%20%7B%20%5Cchi%20%20%7D_%7B%20%5Calpha%20%20%7D%5E%7B%202%20%7D%28n%29%20%7D%5E%7B%20%5Cinfty%20%20%7D%7B%20f%28y%29dy%3D%5Calpha%20%20%7D&height=45&width=261)

卡方分布表

卡方分布表

费希尔曾证明，当 充分大时，近似地有 %5Capprox%20%5Cfrac%20%7B%201%20%7D%7B%202%20%7D%20%7B%20(%7B%20z%20%7D%7B%20%5Calpha%20%20%7D%2B%5Csqrt%20%7B%202n-1%20%7D%20)%20%7D%5E%7B%202%20%7D#card=math&code=%7B%20%5Cchi%20%20%7D%7B%20%5Calpha%20%20%7D%5E%7B%202%20%7D%28n%29%5Capprox%20%5Cfrac%20%7B%201%20%7D%7B%202%20%7D%20%7B%20%28%7B%20z%20%7D_%7B%20%5Calpha%20%20%7D%2B%5Csqrt%20%7B%202n-1%20%7D%20%29%20%7D%5E%7B%202%20%7D&height=37&width=199)。

利用前式可以求得当 时卡方分布上 分位点的近似值。

t 分布

定义

设 #card=math&code=X%5Csim%20N%5Cleft%28%200%20%2C1%20%5Cright%29&height=20&width=91) ，#card=math&code=Y%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft%28%20n%20%5Cright%29&height=23&width=79)，且 相互独立，则称随机变量(统计量)

服从自由度为n的t分布，即为 #card=math&code=t%5Csim%20t%28n%29&height=20&width=57)， 分布又称学生氏(student)分布。

密度函数

%3D%5Cfrac%20%7B%20%5CGamma%20%5B(n%2B1)%2F2%5D%20%7D%7B%20%5Csqrt%20%7B%20%5Cpi%20n%20%7D%20%5CGamma%20%5Cleft(%20n%2F2%20%5Cright)%20%20%7D%20%7B%20(1%2B%5Cfrac%20%7B%20%7B%20t%20%7D%5E%7B%202%20%7D%20%7D%7B%20n%20%7D%20)%20%7D%5E%7B%20-(n%2B1)%2F2%20%7D%2C-%5Cinfty%20%3Ct%3C%5Cinfty#card=math&code=h%28t%29%3D%5Cfrac%20%7B%20%5CGamma%20%5B%28n%2B1%29%2F2%5D%20%7D%7B%20%5Csqrt%20%7B%20%5Cpi%20n%20%7D%20%5CGamma%20%5Cleft%28%20n%2F2%20%5Cright%29%20%20%7D%20%7B%20%281%2B%5Cfrac%20%7B%20%7B%20t%20%7D%5E%7B%202%20%7D%20%7D%7B%20n%20%7D%20%29%20%7D%5E%7B%20-%28n%2B1%29%2F2%20%7D%2C-%5Cinfty%20%3Ct%3C%5Cinfty&height=52&width=367)

图像

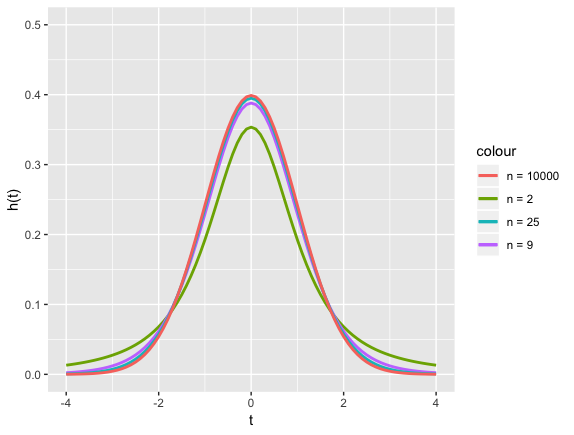
#card=math&code=h%28t%29&height=20&width=28) 的图形关于 对称，当 充分大时，其图形类似于标准正态变量概率密度的图形。但对于较小 ， 分布与 #card=math&code=N%280%2C1%29&height=20&width=52) 分布相差较大。

t 分布分位点

对于给定的 ，满足条件：

%5C%7D%20%3D%5Cint%20%7B%20%7B%20t%20%7D%7B%20%5Calpha%20%20%7D(n)%20%7D%5E%7B%20%5Cinfty%20%20%7D%7B%20h(t)dt%20%7D%20%3D%5Calpha#card=math&code=P%5C%7B%20t%3E%7B%20t%20%7D%7B%20%5Calpha%20%20%7D%28n%29%5C%7D%20%3D%5Cint%20%7B%20%7B%20t%20%7D_%7B%20%5Calpha%20%20%7D%28n%29%20%7D%5E%7B%20%5Cinfty%20%20%7D%7B%20h%28t%29dt%20%7D%20%3D%5Calpha&height=45&width=238)

的点 #card=math&code=%7B%20t%20%7D_%7B%20a%20%7D%5Cleft%28%20n%20%5Cright%29&height=20&width=40) 就是 #card=math&code=t%28n%29&height=20&width=28) 分布上的 分位点。

%20%3D%7B%20-t%20%7D%7B%20a%20%7D%5Cleft(%20n%20%5Cright)#card=math&code=%7B%20t%20%7D%7B%201-a%20%7D%5Cleft%28%20n%20%5Cright%29%20%3D%7B%20-t%20%7D_%7B%20a%20%7D%5Cleft%28%20n%20%5Cright%29&height=20&width=131)

且当 时，对于常用的 的值，就用正态近似：%20%3D%7B%20z%20%7D%7B%20%5Calpha%20%7D#card=math&code=%7B%20t%20%7D%7B%20a%20%7D%5Cleft%28%20n%20%5Cright%29%20%3D%7B%20z%20%7D_%7B%20%5Calpha%20%7D&height=20&width=79)

F 分布

定义

%2CV%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D(%7B%20n%20%7D%7B%202%20%7D)#card=math&code=U%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%28%7B%20n%20%7D%7B%201%20%7D%29%2CV%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%28%7B%20n%20%7D%7B%202%20%7D%29&height=23&width=176)，且 相互独立，则称随机变量  服从自由度为 #card=math&code=%28n_1%2C%20n_2%29&height=20&width=56) 的 分布，记为 #card=math&code=F%5Csim%20F%28%7B%20n%20%7D%7B%201%20%7D%7B%20%2Cn%20%7D_%7B%202%20%7D%29&height=20&width=103)。

概率密度

%3D%5Cfrac%20%7B%20%5CGamma%20%5B(%7B%20n%20%7D%7B%201%20%7D%2B%7B%20n%20%7D%7B%202%20%7D)%2F2%5D%7B%20(%7B%20n%20%7D%7B%201%20%7D%2F%7B%20n%20%7D%7B%202%20%7D)%20%7D%5E%7B%20%7B%20n%20%7D%7B%201%20%7D%2F2%20%7D%7B%20y%20%7D%5E%7B%20(%7B%20n%20%7D%7B%201%20%7D%2F2)-1%20%7D%20%7D%7B%20%5CGamma%20(%7B%20n%20%7D%7B%201%20%7D%2F2)%5CGamma%20(%7B%20n%20%7D%7B%202%20%7D%2F2)%7B%20%5B1%2B(%7B%20n%20%7D%7B%201%20%7Dy%2F%7B%20n%20%7D%7B%202%20%7D)%5D%20%7D%5E%7B%20(%7B%20n%20%7D%7B%201%20%7D%2B%7B%20n%20%7D%7B%202%20%7D)%2F2%20%7D%20%7D%20%2Cy%3E0#card=math&code=%5Cvarphi%20%28y%29%3D%5Cfrac%20%7B%20%5CGamma%20%5B%28%7B%20n%20%7D%7B%201%20%7D%2B%7B%20n%20%7D%7B%202%20%7D%29%2F2%5D%7B%20%28%7B%20n%20%7D%7B%201%20%7D%2F%7B%20n%20%7D%7B%202%20%7D%29%20%7D%5E%7B%20%7B%20n%20%7D%7B%201%20%7D%2F2%20%7D%7B%20y%20%7D%5E%7B%20%28%7B%20n%20%7D%7B%201%20%7D%2F2%29-1%20%7D%20%7D%7B%20%5CGamma%20%28%7B%20n%20%7D%7B%201%20%7D%2F2%29%5CGamma%20%28%7B%20n%20%7D%7B%202%20%7D%2F2%29%7B%20%5B1%2B%28%7B%20n%20%7D%7B%201%20%7Dy%2F%7B%20n%20%7D%7B%202%20%7D%29%5D%20%7D%5E%7B%20%28%7B%20n%20%7D%7B%201%20%7D%2B%7B%20n%20%7D%7B%202%20%7D%29%2F2%20%7D%20%7D%20%2Cy%3E0&height=54&width=386)，其他为 0。

图形

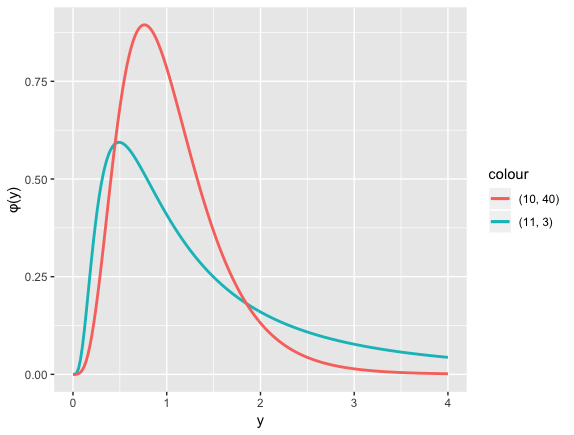
由定义可知，若 #card=math&code=F%5Csim%20F%28%7B%20n%20%7D%7B%201%20%7D%7B%20%2Cn%20%7D%7B%202%20%7D%29&height=20&width=103)，则 #card=math&code=%5Cfrac%20%7B%201%20%7D%7B%20F%20%7D%20%5Csim%20F%28%7B%20n%20%7D%7B%202%20%7D%2C%7B%20n%20%7D%7B%201%20%7D%29&height=37&width=109)

还有性质：%3D%5Cfrac%20%7B%201%20%7D%7B%20%7B%20%7B%20F%20%7D%7B%20%5Calpha%20%20%7D%20%7D(%7B%20n%20%7D%7B%202%20%7D%2C%7B%20n%20%7D%7B%201%20%7D)%20%7D#card=math&code=%7B%20%7B%20F%20%7D%7B%201-%5Calpha%20%20%7D%20%7D%28%7B%20n%20%7D%7B%201%20%7D%2C%7B%20n%20%7D%7B%202%20%7D%29%3D%5Cfrac%20%7B%201%20%7D%7B%20%7B%20%7B%20F%20%7D%7B%20%5Calpha%20%20%7D%20%7D%28%7B%20n%20%7D%7B%202%20%7D%2C%7B%20n%20%7D_%7B%201%20%7D%29%20%7D&height=43&width=196)

分位点

对于给定的 ，满足条件：

%5C%7D%20%3D%5Cint%20%7B%20%7B%20F%20%7D%7B%20%5Calpha%20%20%7D(%7B%20n%20%7D%7B%201%20%7D%2C%7B%20n%20%7D%7B%202%20%7D)%20%7D%5E%7B%20%5Cinfty%20%20%7D%7B%20%5Cvarphi%20(y)dy%3D%5Calpha%20%20%7D#card=math&code=P%5C%7B%20F%3E%7B%20F%20%7D%7B%20%5Calpha%20%20%7D%28%7B%20n%20%7D%7B%201%20%7D%2C%7B%20n%20%7D%7B%202%20%7D%29%5C%7D%20%3D%5Cint%20%7B%20%7B%20F%20%7D%7B%20%5Calpha%20%20%7D%28%7B%20n%20%7D%7B%201%20%7D%2C%7B%20n%20%7D_%7B%202%20%7D%29%20%7D%5E%7B%20%5Cinfty%20%20%7D%7B%20%5Cvarphi%20%28y%29dy%3D%5Calpha%20%20%7D&height=45&width=313)

的点 #card=math&code=%7B%20F%20%7D%7B%20%5Calpha%20%20%7D%28%7B%20n%20%7D%7B%201%20%7D%2C%7B%20n%20%7D%7B%202%20%7D%29&height=20&width=76) 就是 #card=math&code=%7B%20F%20%7D%28%7B%20n%20%7D%7B%201%20%7D%2C%7B%20n%20%7D_%7B%202%20%7D%29&height=20&width=68) 分布的 上 分位点。

类似地有卡方分布， 分布， 分布的下分位点。

常用统计量的分布

1. #card=math&code=%5Cfrac%20%7B%20%5Cbar%20%7B%20X%20%7D%20-%5Cmu%20%20%7D%7B%20%7B%20%5Csigma%20%20%7D%2F%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%7D%20%5Csim%20N%5Cleft%28%200%2C1%20%5Cright%29&height=48&width=128)
2. %20%7B%20S%20%7D%5E%7B%202%20%7D%20%7D%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%20%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft(%20n-1%20%5Cright)#card=math&code=%5Cfrac%20%7B%20%5Cleft%28%20n-1%20%5Cright%29%20%7B%20S%20%7D%5E%7B%202%20%7D%20%7D%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%20%5Csim%20%7B%20%5Cchi%20%20%7D%5E%7B%202%20%7D%5Cleft%28%20n-1%20%5Cright%29&height=45&width=175)
3. 与 相互独立
4. #card=math&code=%5Cfrac%20%7B%20%5Cbar%20%7B%20X%20%7D%20-%5Cmu%20%20%7D%7B%20%7B%20S%20%20%7D%2F%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%7D%5Csim%20t%28n-1%29&height=48&width=131)
5. #card=math&code=%5Cfrac%20%7B%20%7B%20%7B%20S%20%7D%7B%201%20%7D%5E%7B%202%20%7D%20%7D%2F%7B%20%7B%20S%20%7D%7B%202%20%7D%5E%7B%202%20%7D%20%7D%20%7D%7B%20%7B%20%7B%20%5Csigma%20%20%7D%7B%201%20%7D%5E%7B%202%20%7D%20%7D%2F%7B%20%7B%20%5Csigma%20%20%7D%7B%202%20%7D%5E%7B%202%20%7D%20%7D%20%7D%20%5Csim%20F%28%7B%20n%20%7D%7B%201%20%7D-1%2C%7B%20n%20%7D%7B%202%20%7D-1%29&height=50&width=201)
6. 当 时，%20-%5Cleft(%20%7B%20%5Cmu%20%20%7D%7B%201%20%7D-%7B%20%5Cmu%20%20%7D%7B%202%20%7D%20%5Cright)%20%20%7D%7B%20%7B%20S%20%7D%7B%20%5Comega%20%20%7D%5Csqrt%20%7B%20%5Cfrac%20%7B%201%20%7D%7B%20%7B%20n%20%7D%7B%201%20%7D%20%7D%20%2B%5Cfrac%20%7B%201%20%7D%7B%20%7B%20n%20%7D%7B%202%20%7D%20%7D%20%20%7D%20%20%7D%20%5Csim%20t%5Cleft(%20%7B%20n%20%7D%7B%201%20%7D%2B%7B%20n%20%7D%7B%202%20%7D-2%20%5Cright)#card=math&code=%5Cfrac%20%7B%20%5Cleft%28%20%5Cbar%20%7B%20X%20%7D%20-%5Cbar%20%7B%20Y%20%7D%20%20%5Cright%29%20-%5Cleft%28%20%7B%20%5Cmu%20%20%7D%7B%201%20%7D-%7B%20%5Cmu%20%20%7D%7B%202%20%7D%20%5Cright%29%20%20%7D%7B%20%7B%20S%20%7D%7B%20%5Comega%20%20%7D%5Csqrt%20%7B%20%5Cfrac%20%7B%201%20%7D%7B%20%7B%20n%20%7D%7B%201%20%7D%20%7D%20%2B%5Cfrac%20%7B%201%20%7D%7B%20%7B%20n%20%7D%7B%202%20%7D%20%7D%20%20%7D%20%20%7D%20%5Csim%20t%5Cleft%28%20%7B%20n%20%7D%7B%201%20%7D%2B%7B%20n%20%7D%7B%202%20%7D-2%20%5Cright%29&height=64&width=288)，其中 %20%7B%20S%20%7D%7B%201%20%7D%5E%7B%202%20%7D%2B%5Cleft(%20%7B%20n%20%7D%7B%202%20%7D-1%20%5Cright)%20%7B%20S%20%7D%7B%202%20%7D%5E%7B%202%20%7D%20%7D%7B%20%7B%20n%20%7D%7B%201%20%7D%2B%7B%20n%20%7D%7B%202%20%7D-2%20%7D%20%2C%7B%20S%20%7D%7B%20%5Comega%20%20%7D%3D%5Csqrt%20%7B%20%7B%20S%20%7D%7B%20%5Comega%20%20%7D%5E%7B%202%20%7D%20%7D#card=math&code=%7B%20S%20%7D%7B%20%5Comega%20%20%7D%5E%7B%202%20%7D%3D%5Cfrac%20%7B%20%5Cleft%28%20%7B%20n%20%7D%7B%201%20%7D-1%20%5Cright%29%20%7B%20S%20%7D%7B%201%20%7D%5E%7B%202%20%7D%2B%5Cleft%28%20%7B%20n%20%7D%7B%202%20%7D-1%20%5Cright%29%20%7B%20S%20%7D%7B%202%20%7D%5E%7B%202%20%7D%20%7D%7B%20%7B%20n%20%7D%7B%201%20%7D%2B%7B%20n%20%7D%7B%202%20%7D-2%20%7D%20%2C%7B%20S%20%7D%7B%20%5Comega%20%20%7D%3D%5Csqrt%20%7B%20%7B%20S%20%7D%7B%20%5Comega%20%20%7D%5E%7B%202%20%7D%20%7D&height=45&width=316)

一般总体样本均值的分布

大数定律和中心极限定理回顾

在概率论中，我们已经了解了大数定律和中心极限定理（详见前面的章节）：

大数定律讲的是样本均值收敛到总体均值（就是期望），像这个图一样：

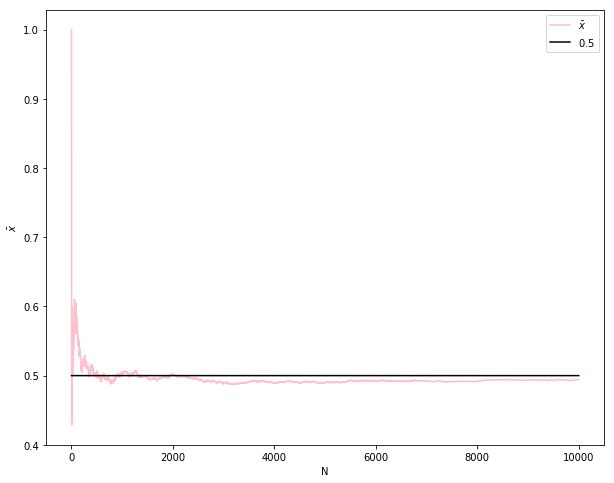
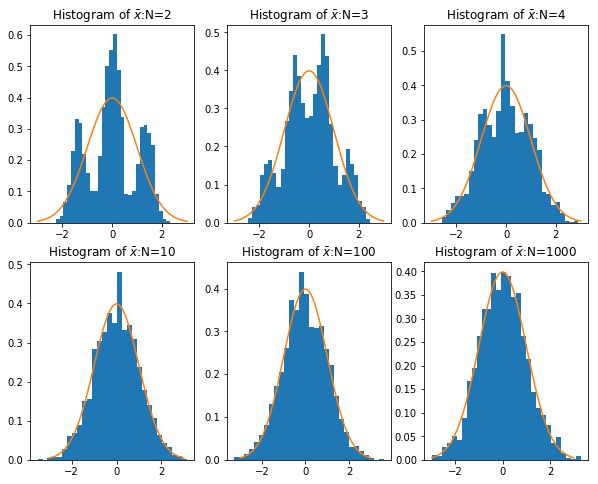
而中心极限定理告诉我们，当样本量足够大时，样本均值的分布慢慢变成正态分布，就像这个图：

示例

代表掷骰子点数的随机变量，，我们做一次试验时掷 2 次骰子，即样本容量为 2，做一次实验的话是一个样本，2 个数字的均值是一个统计量，叫样本均值。

对于这个实验，我们知道总体分布或分布律，为比如一个样本 #card=math&code=%281%2C%204%29&height=20&width=37)，样本均值=2.5，也就是观察值=2.5。我们可以发现，只做一次试验，样本统计量的观察值是不等于总体 的均值 的。

但是，只要我们试验的次数足够多，比如又做了 100 次试验，得到 100 个样本：%2C%20(3%2C%201)%2C%20(1%2C%202)%E2%80%A6#card=math&code=%284%2C%206%29%2C%20%283%2C%201%29%2C%20%281%2C%202%29%E2%80%A6&height=20&width=149) 样本均值的观察值依次为：5，2，1.5，… 大数定律说的就是这些样本均值依概率收敛于总体期望，即 %20%5Capprox%203.5%3DEX#card=math&code=%5Cfrac%20%7B%201%20%7D%7B%20100%20%7D%20%5Cleft%28%202.5%2B5%2B2%2B1.5…%20%5Cright%29%20%5Capprox%203.5%3DEX&height=37&width=273) ，用依概率收敛的符号表示即 。

中心极限定理是说，当样本量足够大时，这些样本均值的观察值是满足正态分布的。

总结

随机变量 。则独立同分布情况下，若样本量很大，由中心极限定理，样本均值 近似地服从参数为 #card=math&code=N%28%5Cmu%20%2C%5Cfrac%20%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%7B%20n%20%7D%20%29&height=41&width=69) 的正态分布。

样本容量如果增大 倍，其标准差会缩小为 ，分布也会变窄。

应用

1. 对于一个随机变量 。若设定样本容量为 ，我们可以得到样本均值 的满足参数为 #card=math&code=N%28%5Cmu%20%2C%5Cfrac%20%7B%20%7B%20%5Csigma%20%20%7D%5E%7B%202%20%7D%20%7D%7B%20n%20%7D%20%29&height=41&width=69) 的正态分布，换个说法，#card=math&code=%5Cfrac%20%7B%20%5Cbar%20%7B%20X%20%7D%20-%5Cmu%20%20%7D%7B%20%7B%20%5Csigma%20%20%7D%2F%7B%20%5Csqrt%20%7B%20n%20%7D%20%20%7D%20%7D%20%5Csim%20N%5Cleft%28%200%2C1%20%5Cright%29&height=48&width=128)。
2. 在分布确定、有了抽样分布的基础上，当我们实际得到一个样本，我们想检验这个样本是否正常。
3. 既然 ， 和 均已知，那么 是一个统计量，即 ，由于单位正态分布天然的计算和观察优势，我们可以利用 得到出现此样本的概率。
4. 比如，我们得到 的概率只有 0.01，那么我们可以认为这是不正常的。因为小概率事件在一次试验中是很难发生的，但也确实有可能发生，比如这里发生的几率就是 0.01。
5. 所以我们如果假定，一次试验当原假设为真时，我们不接受它的概率为 0.05，也就是说弃真错误 ，我们就会抛弃这个样本，觉得它是假的，也就是说我们认为这个样本不正常。另一种说法是，我们有 0.95 的把握认为这个样本是不正常的。
6. 这就是假设检验的基本思想，具体会在之后的章节提到。