10.1 混合高斯 Mixtures of Gaussians

在本章讲义中，我们要讲的是使用期望最大化算法（EM，Expectation-Maximization）来进行密度估计（density estimation）。

一如既往，还是假设我们得到了某一个训练样本集%7D%2C…%2Cx%5E%7B(m)%7D%5C%7D#card=math&code=%5C%7Bx%5E%7B%281%29%7D%2C…%2Cx%5E%7B%28m%29%7D%5C%7D&height=19&width=90)。由于这次是非监督学习（unsupervised learning）环境，所以这些样本就没有什么分类标签了。

我们希望能够获得一个联合分布 %7D%2Cz%5E%7B(i)%7D)%20%3D%20p(x%5E%7B(i)%7D%7Cz%5E%7B(i)%7D)p(z%5E%7B(i)%7D)#card=math&code=p%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%29%20%3D%20p%28x%5E%7B%28i%29%7D%7Cz%5E%7B%28i%29%7D%29p%28z%5E%7B%28i%29%7D%29&height=19&width=175) 来对数据进行建模。其中的 %7D%20%5Csim%20Multinomial(%5Cphi)#card=math&code=z%5E%7B%28i%29%7D%20%5Csim%20Multinomial%28%5Cphi%29&height=19&width=133) （即%7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 是一个以 为参数的多项式分布，其中 ，而参数 给出了 %7D%20%3D%20j)#card=math&code=p%28z%5E%7B%28i%29%7D%20%3D%20j%29&height=19&width=60)），另外 %7D%7Cz%5E%7B(i)%7D%20%3D%20j%20%5Csim%20N(%CE%BC_j%2C%5CSigma_j)#card=math&code=x%5E%7B%28i%29%7D%7Cz%5E%7B%28i%29%7D%20%3D%20j%20%5Csim%20N%28%CE%BC_j%2C%5CSigma_j%29&height=21&width=140) （译者注：%7D%7Cz%5E%7B(i)%7D%20%3D%20j#card=math&code=x%5E%7B%28i%29%7D%7Cz%5E%7B%28i%29%7D%20%3D%20j&height=19&width=65)是一个以 和 为参数的正态分布）。我们设 来表示 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 能取的值的个数。因此，我们这个模型就是在假设每个%7D#card=math&code=x%5E%7B%28i%29%7D&height=16&width=20) 都是从中随机选取%7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18)来生成的，然后 %7D#card=math&code=x%5E%7B%28i%29%7D&height=16&width=20) 就是服从个高斯分布中的一个，而这个高斯分布又取决于%7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18)。这就叫做一个混合高斯模型（mixture of Gaussians model）。 此外还要注意的就是这里的 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 是潜在的随机变量（latent random variables），这就意味着其取值可能还是隐藏的或者未被观测到的。这就会增加这个估计问题（estimation problem）的难度。

我们这个模型的参数也就是 和 。要对这些值进行估计，我们可以写出数据的似然函数（likelihood）：

%20%26%3D%20%5Csum%7Bi%3D1%7D%5Em%20%5Clog%20p(x%5E%7B(i)%7D%3B%5Cphi%2C%5Cmu%2C%5CSigma)%20%5C%5C%0A%26%3D%20%5Csum%7Bi%3D1%7D%5Em%20%5Clog%20%5Csum%7Bz%5E%7B(i)%7D%3D1%7D%5Ek%20p(x%5E%7B(i)%7D%7Cz%5E%7B(i)%7D%3B%5Cmu%2C%5CSigma)p(z%5E%7B(i)%7D%3B%5Cphi)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0Al%28%5Cphi%2C%5Cmu%2C%5CSigma%29%20%26%3D%20%5Csum%7Bi%3D1%7D%5Em%20%5Clog%20p%28x%5E%7B%28i%29%7D%3B%5Cphi%2C%5Cmu%2C%5CSigma%29%20%5C%5C%0A%26%3D%20%5Csum%7Bi%3D1%7D%5Em%20%5Clog%20%5Csum%7Bz%5E%7B%28i%29%7D%3D1%7D%5Ek%20p%28x%5E%7B%28i%29%7D%7Cz%5E%7B%28i%29%7D%3B%5Cmu%2C%5CSigma%29p%28z%5E%7B%28i%29%7D%3B%5Cphi%29%0A%5Cend%7Baligned%7D%0A&height=86&width=284)

然而，如果我们用设上面方程的导数为零来尝试解各个参数，就会发现根本不可能以闭合形式（closed form）来找到这些参数的最大似然估计（maximum likelihood estimates）。（不信的话你自己试试咯。）

随机变量 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18)表示着 %7D#card=math&code=x%5E%7B%28i%29%7D&height=16&width=20) 所属于的 个高斯分布值。这里要注意，如果我们已知 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18)，这个最大似然估计问题就简单很多了。那么就可以把似然函数写成下面这种形式：

%3D%5Csum%7Bi%3D1%7D%5Em%20%5Clog%20p(x%5E%7B(i)%7D%7Cz%5E%7B(i)%7D%3B%5Cmu%2C%5CSigma)%20%2B%20%5Clog%20p(z%5E%7B(i)%7D%3B%5Cphi)%0A#card=math&code=l%28%5Cphi%2C%5Cmu%2C%5CSigma%29%3D%5Csum%7Bi%3D1%7D%5Em%20%5Clog%20p%28x%5E%7B%28i%29%7D%7Cz%5E%7B%28i%29%7D%3B%5Cmu%2C%5CSigma%29%20%2B%20%5Clog%20p%28z%5E%7B%28i%29%7D%3B%5Cphi%29%0A&height=40&width=288)

对上面的函数进行最大化，就能得到对应的参数 和 ：

%7D%3Dj%5C%7D%2C%20%5C%5C%0A%26%5Cmuj%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5Em%201%5C%7Bz%5E%7B(i)%7D%3Dj%5C%7Dx%5E%7B(i)%7D%7D%7B%5Csum%7Bi%3D1%7D%5Em%201%5C%7Bz%5E%7B(i)%7D%3Dj%5C%7D%7D%2C%20%5C%5C%0A%26%5CSigma_j%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5Em%201%5C%7Bz%5E%7B(i)%7D%3Dj%5C%7D(x%5E%7B(i)%7D-%5Cmuj)(x%5E%7B(i)%7D-%5Cmu_j)%5ET%7D%7B%5Csum%7Bi%3D1%7D%5Em%201%5C%7Bz%5E%7B(i)%7D%3Dj%5C%7D%7D.%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%26%5Cphij%3D%5Cfrac%201m%5Csum%7Bi%3D1%7D%5Em%201%5C%7Bz%5E%7B%28i%29%7D%3Dj%5C%7D%2C%20%5C%5C%0A%26%5Cmuj%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5Em%201%5C%7Bz%5E%7B%28i%29%7D%3Dj%5C%7Dx%5E%7B%28i%29%7D%7D%7B%5Csum%7Bi%3D1%7D%5Em%201%5C%7Bz%5E%7B%28i%29%7D%3Dj%5C%7D%7D%2C%20%5C%5C%0A%26%5CSigma_j%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5Em%201%5C%7Bz%5E%7B%28i%29%7D%3Dj%5C%7D%28x%5E%7B%28i%29%7D-%5Cmuj%29%28x%5E%7B%28i%29%7D-%5Cmu_j%29%5ET%7D%7B%5Csum%7Bi%3D1%7D%5Em%201%5C%7Bz%5E%7B%28i%29%7D%3Dj%5C%7D%7D.%0A%5Cend%7Baligned%7D%0A&height=125&width=271)

事实上，我们已经看到了，如果 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 是已知的，那么这个最大似然估计就几乎等同于之前用高斯判别分析模型（Gaussian discriminant analysis model）中对参数进行的估计，唯一不同在于这里的 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 扮演了高斯判别分析当中的分类标签的角色。

1 这里的式子和之前在 PS1 中高斯判别分析的方程还有一些小的区别，这首先是因为在此处我们把 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 泛化为多项式分布（multinomial），而不是伯努利分布（Bernoulli），其次是由于这里针对高斯分布中的每一项使用了一个不同的 。

然而，在密度估计问题里面，%7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 是不知道的。这要怎么办呢？
期望最大化算法（EM，Expectation-Maximization）是一个迭代算法，有两个主要的步骤。针对我们这个问题，在 这一步中，程序是试图去“猜测（guess）” %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 的值。然后在 这一步，就根据上一步的猜测来对模型参数进行更新。由于在 这一步当中我们假设（pretend）了上一步是对的，那么最大化的过程就简单了。下面是这个算法：

 重复下列过程直到收敛（convergence）: {

  （-步骤）对每个 , 设

%7D%20%3A%3D%20p(z%5E%7B(i)%7D%3Dj%7Cx%5E%7B(i)%7D%3B%5Cphi%2C%5Cmu%2C%5CSigma)%0A#card=math&code=w_j%5E%7B%28i%29%7D%20%3A%3D%20p%28z%5E%7B%28i%29%7D%3Dj%7Cx%5E%7B%28i%29%7D%3B%5Cphi%2C%5Cmu%2C%5CSigma%29%0A&height=23&width=171)

  （-步骤）更新参数：

%7D%2C%20%5C%5C%0A%26%5Cmuj%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5Em%20wj%5E%7B(i)%7Dx%5E%7B(i)%7D%7D%7B%5Csum%7Bi%3D1%7D%5Em%20wj%5E%7B(i)%7D%7D%2C%20%5C%5C%0A%26%5CSigma_j%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5Em%20wj%5E%7B(i)%7D(x%5E%7B(i)%7D-%5Cmu_j)(x%5E%7B(i)%7D-%5Cmu_j)%5ET%7D%7B%5Csum%7Bi%3D1%7D%5Em%20wj%5E%7B(i)%7D%7D.%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%26%5Cphi_j%3D%5Cfrac%201m%5Csum%7Bi%3D1%7D%5Em%20wj%5E%7B%28i%29%7D%2C%20%5C%5C%0A%26%5Cmu_j%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5Em%20wj%5E%7B%28i%29%7Dx%5E%7B%28i%29%7D%7D%7B%5Csum%7Bi%3D1%7D%5Em%20wj%5E%7B%28i%29%7D%7D%2C%20%5C%5C%0A%26%5CSigma_j%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5Em%20wj%5E%7B%28i%29%7D%28x%5E%7B%28i%29%7D-%5Cmu_j%29%28x%5E%7B%28i%29%7D-%5Cmu_j%29%5ET%7D%7B%5Csum%7Bi%3D1%7D%5Em%20w_j%5E%7B%28i%29%7D%7D.%0A%5Cend%7Baligned%7D%0A&height=144&width=230)

}

在 步骤中，在给定 %7D#card=math&code=x%5E%7B%28i%29%7D&height=16&width=20) 以及使用当前参数设置（current setting of our parameters）情况下，我们计算出了参数 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 的后验概率（posterior probability）。使用贝叶斯规则（Bayes rule），就得到下面的式子：

%7D%3Dj%7Cx%5E%7B(i)%7D%3B%5Cphi%2C%5Cmu%2C%5CSigma)%3D%0A%5Cfrac%7Bp(x%5E%7B(i)%7D%7Cz%5E%7B(i)%7D%3Dj%3B%5Cmu%2C%5CSigma)p(z%5E%7B(i)%7D%3Dj%3B%5Cphi)%7D%0A%7B%5Csum%7Bl%3D1%7D%5Ek%20p(x%5E%7B(i)%7D%7Cz%5E%7B(i)%7D%3Dl%3B%5Cmu%2C%5CSigma)p(z%5E%7B(i)%7D%3Dl%3B%5Cphi)%7D%0A#card=math&code=p%28z%5E%7B%28i%29%7D%3Dj%7Cx%5E%7B%28i%29%7D%3B%5Cphi%2C%5Cmu%2C%5CSigma%29%3D%0A%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%7Cz%5E%7B%28i%29%7D%3Dj%3B%5Cmu%2C%5CSigma%29p%28z%5E%7B%28i%29%7D%3Dj%3B%5Cphi%29%7D%0A%7B%5Csum%7Bl%3D1%7D%5Ek%20p%28x%5E%7B%28i%29%7D%7Cz%5E%7B%28i%29%7D%3Dl%3B%5Cmu%2C%5CSigma%29p%28z%5E%7B%28i%29%7D%3Dl%3B%5Cphi%29%7D%0A&height=42&width=367)

上面的式子中，%7D%3Dj%7Cx%5E%7B(i)%7D%3B%5Cphi%2C%5Cmu%2C%5CSigma)#card=math&code=p%28z%5E%7B%28i%29%7D%3Dj%7Cx%5E%7B%28i%29%7D%3B%5Cphi%2C%5Cmu%2C%5CSigma%29&height=19&width=127) 是通过评估一个高斯分布的密度得到的，这个高斯分布的均值为 ，对%7D#card=math&code=x%5E%7B%28i%29%7D&height=16&width=20)的协方差为；%7D%20%3D%20j%3B%5Cphi)#card=math&code=p%28z%5E%7B%28i%29%7D%20%3D%20j%3B%5Cphi%29&height=19&width=74) 是通过 得到，以此类推。在 步骤中计算出来的 %7D#card=math&code=w_j%5E%7B%28i%29%7D&height=23&width=21) 代表了我们对 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 这个值的“弱估计（soft guesses）”。

2 这里用的词汇“弱（soft）”是指我们对概率进行猜测，从 这样一个闭区间进行取值；而与之对应的“强（hard）”值得是单次最佳猜测，例如从集合 或者 中取一个值。

另外在 步骤中进行的更新还要与 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 已知之后的方程式进行对比。它们是相同的，不同之处只在于之前使用的指示函数（indicator functions），指示每个数据点所属的高斯分布，而这里换成了 %7D#card=math&code=w_j%5E%7B%28i%29%7D&height=23&width=21)。

算法也让人想起 均值聚类算法，而在 均值聚类算法中对聚类重心 #card=math&code=c%28i%29&height=16&width=20) 进行了“强（hard）”赋值，而在 算法中，对%7D#card=math&code=w_j%5E%7B%28i%29%7D&height=23&width=21) 进行的是“弱（soft）”赋值。与 均值算法类似， 算法也容易导致局部最优，所以使用不同的初始参数（initial parameters）进行重新初始化（reinitializing），可能是个好办法。

很明显， 算法对 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 进行重复的猜测，这种思路很自然；但这个算法是怎么产生的，以及我们能否确保这个算法的某些特性，例如收敛性之类的？在下一章的讲义中，我们会讲解一种对 算法更泛化的解读，这样我们就可以在其他的估计问题中轻松地使用 算法了，只要这些问题也具有潜在变量（latent variables），并且还能够保证收敛。

10.2 期望最大化算法 EM algorithm

在前面的若干讲义中，我们已经讲过了期望最大化算法（EM algorithm），使用场景是对一个高斯混合模型进行拟合（fitting a mixture of Gaussians）。在本章里面，我们要给出期望最大化算法（EM algorithm）的更广泛应用，并且演示如何应用于一个大系列的具有潜在变量（latent variables）的估计问题（estimation problems）。我们的讨论从 Jensen 不等式（Jensen’s inequality） 开始，这是一个非常有用的结论。

10.2.1 Jensen 不等式（Jensen’s inequality）

设 为一个函数，其定义域（domain）为整个实数域（set of real numbers）。这里要回忆一下，如果函数 的二阶导数 %20%5Cge%200#card=math&code=f%27%27%28x%29%20%5Cge%200&height=17&width=57) （其中的 ），则函数 为一个凸函数（convex function）。如果输入的为向量变量，那么这个函数就泛化了，这时候该函数的海森矩阵（hessian） 就是一个半正定矩阵（positive semi-definite ）。如果对于所有的 ，都有二阶导数 %20%3E%200#card=math&code=f%27%27%28x%29%20%3E%200&height=17&width=57)，那么我们称这个函数 是严格凸函数（对应向量值作为变量的情况，对应的条件就是海森矩阵必须为正定，写作 ）。这样就可以用如下方式来表述 Jensen 不等式：

定理（Theorem）： 设 是一个凸函数，且设 是一个随机变量（random variable）。然后则有：

%5D%20%5Cge%20f(EX).%0A#card=math&code=E%5Bf%28X%29%5D%20%5Cge%20f%28EX%29.%0A&height=16&width=109)

译者注：函数的期望大于等于期望的函数值

此外，如果函数 是严格凸函数，那么 %5D%20%3D%20f(EX)#card=math&code=E%5Bf%28X%29%5D%20%3D%20f%28EX%29&height=16&width=105) 当且仅当 的概率（probability）为 的时候成立（例如 是一个常数）。

还记得我们之前的约定（convention）吧，写期望（expectations）的时候可以偶尔去掉括号（parentheses），所以在上面的定理中， %20%3D%20f(E%5BX%5D)#card=math&code=f%28EX%29%20%3D%20f%28E%5BX%5D%29&height=16&width=105)。

为了容易理解这个定理，可以参考下面的图：

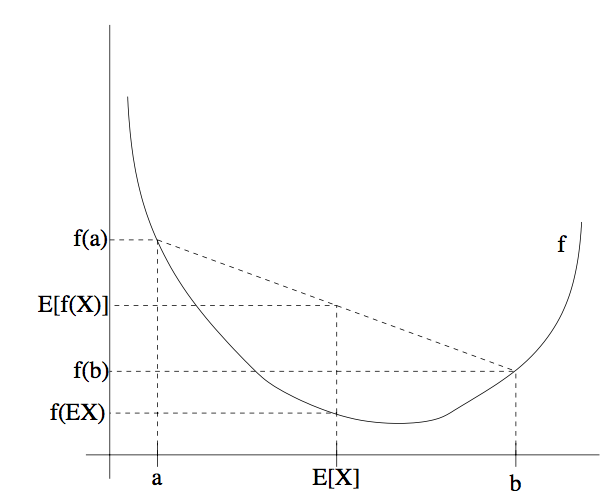
上图中， 是一个凸函数，在图中用实线表示。另外 是一个随机变量，有 的概率（chance）取值为 ，另外有 的概率取值为 （在图中 轴上标出了）。这样， 的期望值就在图中所示的 和 的中点位置。

图中在 轴上也标出了 #card=math&code=f%28a%29&height=16&width=24), #card=math&code=f%28b%29&height=16&width=24) 和 #card=math&code=f%28E%5BX%5D%29&height=16&width=47)。接下来函数的期望值 %5D#card=math&code=E%5Bf%28X%29%5D&height=16&width=47) 在 轴上就处于 #card=math&code=f%28a%29&height=16&width=24) 和 #card=math&code=f%28b%29&height=16&width=24) 之间的中点的位置。如图中所示，在这个例子中由于 是凸函数，很明显 %5D%20%E2%89%A5%20f(EX)#card=math&code=E%5Bf%28X%29%5D%20%E2%89%A5%20f%28EX%29&height=16&width=105)。

顺便说一下，很多人都记不住不等式的方向，所以就不妨用画图来记住，这是很好的方法，还可以通过图像很快来找到答案。

备注。 回想一下，当且仅当 是严格凸函数（[strictly] convex）的时候， 是严格凹函数（[strictly] concave）（例如，二阶导数 %5Cle%200#card=math&code=f%27%27%28x%29%5Cle%200&height=17&width=57) 或者其海森矩阵 ）。Jensen 不等式也适用于凹函数（concave），但不等式的方向要反过来，也就是对于凹函数，%5D%20%5Cle%20f(EX)#card=math&code=E%5Bf%28X%29%5D%20%5Cle%20f%28EX%29&height=16&width=105)。

10.2.2 期望最大化算法（EM algorithm）

假如我们有一个估计问题（estimation problem），其中由训练样本集 %7D%2C%20…%2C%20x%5E%7B(m)%7D%5C%7D#card=math&code=%5C%7Bx%5E%7B%281%29%7D%2C%20…%2C%20x%5E%7B%28m%29%7D%5C%7D&height=19&width=90) 包含了 个独立样本。我们用模型 #card=math&code=p%28x%2C%20z%29&height=16&width=37) 对数据进行建模，拟合其参数（parameters），其中的似然函数（likelihood）如下所示：

%20%26%3D%20%5Csum%7Bi%3D1%7D%5Em%5Clog%20p(x%3B%5Ctheta)%20%5C%5C%0A%26%3D%20%5Csum%7Bi%3D1%7D%5Em%5Clog%5Csumz%20p(x%2Cz%3B%5Ctheta)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0Al%28%5Ctheta%29%20%26%3D%20%5Csum%7Bi%3D1%7D%5Em%5Clog%20p%28x%3B%5Ctheta%29%20%5C%5C%0A%26%3D%20%5Csum_%7Bi%3D1%7D%5Em%5Clog%5Csum_z%20p%28x%2Cz%3B%5Ctheta%29%0A%5Cend%7Baligned%7D%0A&height=82&width=156)

然而，确切地找到对参数 的最大似然估计（maximum likelihood estimates）可能会很难。此处的 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 是一个潜在的随机变量（latent random variables）；通常情况下，如果 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 事先得到了，然后再进行最大似然估计，就容易多了。

这种环境下，使用期望最大化算法（EM algorithm）就能很有效地实现最大似然估计（maximum likelihood estimation）。明确地对似然函数#card=math&code=l%28%5Ctheta%29&height=16&width=20)进行最大化可能是很困难的，所以我们的策略就是使用一种替代，在 步骤 构建一个 的下限（lower-bound），然后在 步骤 对这个下限进行优化。

对于每个 ，设 是某个对 的分布（%20%3D%201%2C%20Q_i(z)%5Cge%200#card=math&code=%5Csum_z%20Q_i%28z%29%20%3D%201%2C%20Q_i%28z%29%5Cge%200&height=32&width=142)）。则有下列各式：

%7D%3B%5Ctheta)%20%26%3D%20%5Csumi%5Clog%5Csum%7Bz%5E%7B(i)%7D%7Dp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%26(1)%20%5C%5C%0A%26%3D%20%5Csumi%5Clog%5Csum%7Bz%5E%7B(i)%7D%7DQi(z%5E%7B(i)%7D)%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%7D%7BQ_i(z%5E%7B(i)%7D)%7D%20%26(2)%5C%5C%0A%26%5Cge%20%5Csum_i%5Csum%7Bz%5E%7B(i)%7D%7DQi(z%5E%7B(i)%7D)%5Clog%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%7D%7BQ_i(z%5E%7B(i)%7D)%7D%26(3)%20%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Csum_i%5Clog%20p%28x%5E%7B%28i%29%7D%3B%5Ctheta%29%20%26%3D%20%5Csum_i%5Clog%5Csum%7Bz%5E%7B%28i%29%7D%7Dp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%26%281%29%20%5C%5C%0A%26%3D%20%5Csumi%5Clog%5Csum%7Bz%5E%7B%28i%29%7D%7DQi%28z%5E%7B%28i%29%7D%29%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%7D%7BQ_i%28z%5E%7B%28i%29%7D%29%7D%20%26%282%29%5C%5C%0A%26%5Cge%20%5Csum_i%5Csum%7Bz%5E%7B%28i%29%7D%7DQ_i%28z%5E%7B%28i%29%7D%29%5Clog%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%7D%7BQ_i%28z%5E%7B%28i%29%7D%29%7D%26%283%29%20%0A%5Cend%7Baligned%7D%0A&height=127&width=346)

1 如果 是连续的，那么 就是一个密度函数（density），上面讨论中提到的对 的求和（summations）就要用对 的积分（integral）来替代。

上面推导（derivation）的最后一步使用了 Jensen 不等式（Jensen’s inequality）。其中的 %20%3D%20log%20x#card=math&code=f%28x%29%20%3D%20log%20x&height=16&width=68) 是一个凹函数（concave function），因为其二阶导数 %20%3D%20-1%2Fx%5E2%20%3C%200#card=math&code=f%27%27%28x%29%20%3D%20-1%2Fx%5E2%20%3C%200&height=18&width=113) 在整个定义域（domain） 上都成立。

此外，上式的求和中的单项：

%7D%7DQi(z%5E%7B(i)%7D)%5B%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%7D%7BQ_i(z%5E%7B(i)%7D)%7D%5D%0A#card=math&code=%5Csum%7Bz%5E%7B%28i%29%7D%7DQ_i%28z%5E%7B%28i%29%7D%29%5B%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%7D%7BQ_i%28z%5E%7B%28i%29%7D%29%7D%5D%0A&height=45&width=152)

是变量（quantity）%7D%2C%20z%5E%7B(i)%7D%3B%20%5Ctheta)%2FQ_i(z%5E%7B(i)%7D)%5D#card=math&code=%5Bp%28x%5E%7B%28i%29%7D%2C%20z%5E%7B%28i%29%7D%3B%20%5Ctheta%29%2FQ_i%28z%5E%7B%28i%29%7D%29%5D&height=19&width=132) 基于 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 的期望，其中 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 是根据 给定的分布确定。然后利用 Jensen 不等式（Jensen’s inequality），就得到了：

%7D%5Csim%20Qi%7D%5B%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%7D%7BQ_i(z%5E%7B(i)%7D)%7D%5D)%5Cge%0AE%7Bz%5E%7B(i)%7D%5Csim%20Qi%7D%5Bf(%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%7D%7BQ_i(z%5E%7B(i)%7D)%7D)%5D%0A#card=math&code=f%28E%7Bz%5E%7B%28i%29%7D%5Csim%20Qi%7D%5B%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%7D%7BQ_i%28z%5E%7B%28i%29%7D%29%7D%5D%29%5Cge%0AE%7Bz%5E%7B%28i%29%7D%5Csim%20Q_i%7D%5Bf%28%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%7D%7BQ_i%28z%5E%7B%28i%29%7D%29%7D%29%5D%0A&height=41&width=315)

其中上面的角标 %7D%5Csim%20Q_i%E2%80%9D#card=math&code=%E2%80%9Cz%5E%7B%28i%29%7D%5Csim%20Q_i%E2%80%9D&height=18&width=65) 就表明这个期望是对于依据分布 来确定的 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 的。这样就可以从等式 #card=math&code=%282%29&height=16&width=17) 推导出等式 #card=math&code=%283%29&height=16&width=17)。

接下来，对于任意的一个分布 ，上面的等式 #card=math&code=%283%29&height=16&width=17) 就给出了似然函数 #card=math&code=l%28%5Ctheta%29&height=16&width=20) 的下限（lower-bound）。那么对于 有很多种选择。咱们该选哪个呢？如果我们对参数 有某种当前的估计，很自然就可以设置这个下限为 这个值。也就是，针对当前的 值，我们令上面的不等式中的符号为等号。（稍后我们能看到，这样就能证明，随着 迭代过程的进行，似然函数 #card=math&code=l%28%5Ctheta%29&height=16&width=20) 就会单调递增（increases monotonically）。）

为了让上面的限定值（bound）与 特定值（particular value）联系紧密（tight），我们需要上面推导过程中的 Jensen 不等式这一步中等号成立。要让这个条件成立，我们只需确保是在对一个常数值随机变量（“constant”-valued random variable）求期望。也就是需要：

%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%7D%7BQ_i(z%5E%7B(i)%7D)%7D%3Dc%0A#card=math&code=%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%7D%7BQ_i%28z%5E%7B%28i%29%7D%29%7D%3Dc%0A&height=41&width=102)

其中常数 不依赖 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18)。要实现这一条件，只需满足：

%7D)%5Cpropto%20p(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%0A#card=math&code=Q_i%28z%5E%7B%28i%29%7D%29%5Cpropto%20p%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%0A&height=19&width=136)

实际上，由于我们已知 %7D)%20%3D%201#card=math&code=%5Csum_z%20Q_i%28z%5E%7B%28i%29%7D%29%20%3D%201&height=32&width=90)（因为这是一个分布），这就进一步表明：

%7D)%20%26%3D%20%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%7D%7B%5Csum_z%20p(x%5E%7B(i)%7D%2Cz%3B%5Ctheta)%7D%20%5C%5C%0A%26%3D%20%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%7D%7Bp(x%5E%7B(i)%7D%3B%5Ctheta)%7D%20%5C%5C%0A%26%3D%20p(z%5E%7B(i)%7D%7Cx%5E%7B(i)%7D%3B%5Ctheta)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0AQ_i%28z%5E%7B%28i%29%7D%29%20%26%3D%20%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%7D%7B%5Csum_z%20p%28x%5E%7B%28i%29%7D%2Cz%3B%5Ctheta%29%7D%20%5C%5C%0A%26%3D%20%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%7D%7Bp%28x%5E%7B%28i%29%7D%3B%5Ctheta%29%7D%20%5C%5C%0A%26%3D%20p%28z%5E%7B%28i%29%7D%7Cx%5E%7B%28i%29%7D%3B%5Ctheta%29%0A%5Cend%7Baligned%7D%0A&height=102&width=156)

因此，在给定 %7D#card=math&code=x%5E%7B%28i%29%7D&height=16&width=20) 和参数 的设置下，我们可以简单地把 设置为 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 的后验分布（posterior distribution）。

接下来，对 的选择，等式 #card=math&code=%283%29&height=16&width=17) 就给出了似然函数对数（log likelihood）的一个下限，而似然函数（likelihood）正是我们要试图求最大值（maximize）的。这就是 步骤。接下来在算法的 步骤中，就最大化等式 #card=math&code=%283%29&height=16&width=17) 当中的方程，然后得到新的参数 。重复这两个步骤，就是完整的 算法，如下所示：

 重复下列过程直到收敛（convergence）: {

  （ 步骤）对每个 ，设

%7D)%3A%3Dp(z%5E%7B(i)%7D%7Cx%5E%7B(i)%7D%3B%5Ctheta)%0A#card=math&code=Q_i%28z%5E%7B%28i%29%7D%29%3A%3Dp%28z%5E%7B%28i%29%7D%7Cx%5E%7B%28i%29%7D%3B%5Ctheta%29%0A&height=19&width=138)

  （ 步骤） 设

%7D%7DQi(z%5E%7B(i)%7D)log%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%7D%7BQ_i(z%5E%7B(i)%7D)%7D%0A#card=math&code=%5Ctheta%20%3A%3D%20arg%5Cmax%5Ctheta%5Csumi%5Csum%7Bz%5E%7B%28i%29%7D%7DQ_i%28z%5E%7B%28i%29%7D%29log%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%7D%7BQ_i%28z%5E%7B%28i%29%7D%29%7D%0A&height=45&width=262)

}

怎么才能知道这个算法是否会收敛（converge）呢？设 %7D#card=math&code=%5Ctheta%5E%7B%28t%29%7D&height=16&width=18) 和 %7D#card=math&code=%5Ctheta%5E%7B%28t%2B1%29%7D&height=16&width=30) 是上面 迭代过程中的某两个参数（parameters）。接下来我们就要证明一下 %7D)%5Cle%20l(%5Ctheta%5E%7B(t%2B1)%7D)#card=math&code=l%28%5Ctheta%5E%7B%28t%29%7D%29%5Cle%20l%28%5Ctheta%5E%7B%28t%2B1%29%7D%29&height=19&width=96)，这就表明 迭代过程总是让似然函数对数（log-likelihood）单调递增（monotonically improves）。证明这个结论的关键就在于对 的选择中。在上面迭代中，参数的起点设为 %7D#card=math&code=%5Ctheta%5E%7B%28t%29%7D&height=16&width=18)，我们就可以选择 %7D(z%5E%7B(i)%7D)%3A%20%3D%20p(z%5E%7B(i)%7D%7Cx%5E%7B(i)%7D%3B%5Ctheta%5E%7B(t)%7D)#card=math&code=Q_i%5E%7B%28t%29%7D%28z%5E%7B%28i%29%7D%29%3A%20%3D%20p%28z%5E%7B%28i%29%7D%7Cx%5E%7B%28i%29%7D%3B%5Ctheta%5E%7B%28t%29%7D%29&height=21&width=157)。之前我们已经看到了，正如等式 #card=math&code=%283%29&height=16&width=17) 的推导过程中所示，这样选择能保证 Jensen 不等式的等号成立，因此：

%7D)%3D%5Csumi%5Csum%7Bz%5E%7B(i)%7D%7DQi%5E%7B(t)%7D(z%5E%7B(i)%7D)log%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta%5E%7B(t)%7D)%7D%7BQ_i%5E%7B(t)%7D(z%5E%7B(i)%7D)%7D%0A#card=math&code=l%28%5Ctheta%5E%7B%28t%29%7D%29%3D%5Csum_i%5Csum%7Bz%5E%7B%28i%29%7D%7DQ_i%5E%7B%28t%29%7D%28z%5E%7B%28i%29%7D%29log%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%5E%7B%28t%29%7D%29%7D%7BQ_i%5E%7B%28t%29%7D%28z%5E%7B%28i%29%7D%29%7D%0A&height=45&width=255)

参数 %7D#card=math&code=%5Ctheta%5E%7B%28t%2B1%29%7D&height=16&width=30) 可以通过对上面等式中等号右侧进行最大化而得到。因此：

%7D)%20%26%5Cge%20%5Csumi%5Csum%7Bz%5E%7B(i)%7D%7DQi%5E%7B(t)%7D(z%5E%7B(i)%7D)log%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta%5E%7B(t%2B1)%7D)%7D%7BQ_i%5E%7B(t)%7D(z%5E%7B(i)%7D)%7D%20%26(4)%5C%5C%0A%26%5Cge%20%5Csum_i%5Csum%7Bz%5E%7B(i)%7D%7DQi%5E%7B(t)%7D(z%5E%7B(i)%7D)log%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta%5E%7B(t)%7D)%7D%7BQ_i%5E%7B(t)%7D(z%5E%7B(i)%7D)%7D%20%26(5)%5C%5C%0A%26%3D%20l(%5Ctheta%5E%7B(t)%7D)%20%26(6)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0Al%28%5Ctheta%5E%7B%28t%2B1%29%7D%29%20%26%5Cge%20%5Csum_i%5Csum%7Bz%5E%7B%28i%29%7D%7DQi%5E%7B%28t%29%7D%28z%5E%7B%28i%29%7D%29log%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%5E%7B%28t%2B1%29%7D%29%7D%7BQ_i%5E%7B%28t%29%7D%28z%5E%7B%28i%29%7D%29%7D%20%26%284%29%5C%5C%0A%26%5Cge%20%5Csum_i%5Csum%7Bz%5E%7B%28i%29%7D%7DQ_i%5E%7B%28t%29%7D%28z%5E%7B%28i%29%7D%29log%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%5E%7B%28t%29%7D%29%7D%7BQ_i%5E%7B%28t%29%7D%28z%5E%7B%28i%29%7D%29%7D%20%26%285%29%5C%5C%0A%26%3D%20l%28%5Ctheta%5E%7B%28t%29%7D%29%20%26%286%29%0A%5Cend%7Baligned%7D%0A&height=110&width=329)

上面的第一个不等式推自：

%5Cge%20%5Csumi%5Csum%7Bz%5E%7B(i)%7D%7DQi(z%5E%7B(i)%7D)log%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%7D%7BQ_i(z%5E%7B(i)%7D)%7D%0A#card=math&code=l%28%5Ctheta%29%5Cge%20%5Csum_i%5Csum%7Bz%5E%7B%28i%29%7D%7DQ_i%28z%5E%7B%28i%29%7D%29log%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%7D%7BQ_i%28z%5E%7B%28i%29%7D%29%7D%0A&height=45&width=223)

上面这个不等式对于任意值的 和 都成立，尤其当 %7D%2C%20%5Ctheta%20%3D%20%5Ctheta%5E%7B(t%2B1)%7D#card=math&code=Q_i%20%3D%20Q_i%5E%7B%28t%29%7D%2C%20%5Ctheta%20%3D%20%5Ctheta%5E%7B%28t%2B1%29%7D&height=21&width=117)。要得到等式 #card=math&code=%285%29&height=16&width=17)，我们要利用 %7D#card=math&code=%5Ctheta%5E%7B%28t%2B1%29%7D&height=16&width=30) 的选择能够保证：

%7D%7DQi(z%5E%7B(i)%7D)log%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%7D%7BQ_i(z%5E%7B(i)%7D)%7D%0A#card=math&code=arg%5Cmax%5Ctheta%20%5Csumi%5Csum%7Bz%5E%7B%28i%29%7D%7DQ_i%28z%5E%7B%28i%29%7D%29log%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%7D%7BQ_i%28z%5E%7B%28i%29%7D%29%7D%0A&height=45&width=234)

这个式子对 %7D#card=math&code=%5Ctheta%5E%7B%28t%2B1%29%7D&height=16&width=30) 得到的值必须大于等于 %7D#card=math&code=%5Ctheta%5E%7B%28t%29%7D&height=16&width=18) 得到的值。最后，推导等式#card=math&code=%286%29&height=16&width=17) 的这一步，正如之前所示，因为在选择的时候我们选的 %7D#card=math&code=Q_i%5E%7B%28t%29%7D&height=21&width=23) 就是要保证 Jensen 不等式对 %7D#card=math&code=%5Ctheta%5E%7B%28t%29%7D&height=16&width=18) 等号成立。

因此， 算法就能够导致似然函数（likelihood）的单调收敛。在我们推导 算法的过程中，我们要一直运行该算法到收敛。得到了上面的结果之后，可以使用一个合理的收敛检测（reasonable convergence test）来检查在成功的迭代（successive iterations）之间的 #card=math&code=l%28%5Ctheta%29&height=16&width=20) 的增长是否小于某些容忍参数（tolerance parameter），如果 算法对 #card=math&code=l%28%5Ctheta%29&height=16&width=20) 的增大速度很慢，就声明收敛（declare convergence）。

备注。 如果我们定义

%3D%5Csumi%5Csum%7Bz%5E%7B(i)%7D%7DQi(z%5E%7B(i)%7D)log%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Ctheta)%7D%7BQ_i(z%5E%7B(i)%7D)%7D%0A#card=math&code=J%28Q%2C%20%5Ctheta%29%3D%5Csum_i%5Csum%7Bz%5E%7B%28i%29%7D%7DQ_i%28z%5E%7B%28i%29%7D%29log%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Ctheta%29%7D%7BQ_i%28z%5E%7B%28i%29%7D%29%7D%0A&height=45&width=244)

通过我们之前的推导，就能知道 %20%E2%89%A5%20J(Q%2C%20%5Ctheta)#card=math&code=l%28%5Ctheta%29%20%E2%89%A5%20J%28Q%2C%20%5Ctheta%29&height=16&width=81)。这样 算法也可看作是在 上的坐标上升（coordinate ascent），其中 步骤在 上对 进行了最大化（自己检查哈），然后 步骤则在 上对 进行最大化。

10.2.3 高斯混合模型回顾（Mixture of Gaussians revisited ）

有了对 算法的广义定义（general definition）之后，我们就可以回顾一下之前的高斯混合模型问题，其中要拟合的参数有 和。为了避免啰嗦，这里就只给出在 步骤中对 和 进行更新的推导，关于 的更新推导就由读者当作练习自己来吧。

步骤很简单。还是按照上面的算法推导过程，只需要计算：

%7D%3DQ_i(z%5E%7B(i)%7D%3Dj)%3DP(z%5E%7B(i)%7D%3Dj%7Cx%5E%7B(i)%7D%3B%5Cphi%2C%5Cmu%2C%5CSigma)%0A#card=math&code=w_j%5E%7B%28i%29%7D%3DQ_i%28z%5E%7B%28i%29%7D%3Dj%29%3DP%28z%5E%7B%28i%29%7D%3Dj%7Cx%5E%7B%28i%29%7D%3B%5Cphi%2C%5Cmu%2C%5CSigma%29%0A&height=23&width=256)

这里面的 %7D%20%3D%20j)%E2%80%9D#card=math&code=%E2%80%9CQ_i%28z%5E%7B%28i%29%7D%20%3D%20j%29%E2%80%9D&height=19&width=81) 表示的是在分布 上 %7D#card=math&code=z%5E%7B%28i%29%7D&height=16&width=18) 取值 的概率。

接下来在 步骤，就要最大化关于参数 的值：

%7D%7DQi(z%5E%7B(i)%7D)log%5Cfrac%7Bp(x%5E%7B(i)%7D%2Cz%5E%7B(i)%7D%3B%5Cphi%2C%5Cmu%2C%5CSigma)%7D%7BQ_i(z%5E%7B(i)%7D)%7D%5C%5C%0A%26%3D%20%5Csum%7Bi%3D1%7D%5Em%5Csum%7Bj%3D1%7D%5EkQ_i(z%5E%7B(i)%7D%3Dj)log%5Cfrac%7Bp(x%5E%7B(i)%7D%7Cz%5E%7B(i)%7D%3Dj%3B%5Cmu%2C%5CSigma)p(z%5E%7B(i)%7D%3Dj%3B%5Cphi)%7D%7BQ_i(z%5E%7B(i)%7D%3Dj)%7D%20%5C%5C%0A%26%3D%20%5Csum%7Bi%3D1%7D%5Em%5Csum%7Bj%3D1%7D%5Ekw_j%5E%7B(i)%7Dlog%5Cfrac%7B%5Cfrac%7B1%7D%7B(2%5Cpi)%5E%7Bn%2F2%7D%7C%5CSigma_j%7C%5E%7B1%2F2%7D%7Dexp(-%5Cfrac%2012(x%5E%7B(i)%7D-%5Cmu_j)%5ET%5CSigma_j%5E%7B-1%7D(x%5E%7B(i)%7D-%5Cmu_j))%5Ccdot%5Cphi_j%7D%7Bw_j%5E%7B(i)%7D%7D%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Csum%7Bi%3D1%7D%5Em%26%5Csum%7Bz%5E%7B%28i%29%7D%7DQ_i%28z%5E%7B%28i%29%7D%29log%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%2Cz%5E%7B%28i%29%7D%3B%5Cphi%2C%5Cmu%2C%5CSigma%29%7D%7BQ_i%28z%5E%7B%28i%29%7D%29%7D%5C%5C%0A%26%3D%20%5Csum%7Bi%3D1%7D%5Em%5Csum%7Bj%3D1%7D%5EkQ_i%28z%5E%7B%28i%29%7D%3Dj%29log%5Cfrac%7Bp%28x%5E%7B%28i%29%7D%7Cz%5E%7B%28i%29%7D%3Dj%3B%5Cmu%2C%5CSigma%29p%28z%5E%7B%28i%29%7D%3Dj%3B%5Cphi%29%7D%7BQ_i%28z%5E%7B%28i%29%7D%3Dj%29%7D%20%5C%5C%0A%26%3D%20%5Csum%7Bi%3D1%7D%5Em%5Csum_%7Bj%3D1%7D%5Ekw_j%5E%7B%28i%29%7Dlog%5Cfrac%7B%5Cfrac%7B1%7D%7B%282%5Cpi%29%5E%7Bn%2F2%7D%7C%5CSigma_j%7C%5E%7B1%2F2%7D%7Dexp%28-%5Cfrac%2012%28x%5E%7B%28i%29%7D-%5Cmu_j%29%5ET%5CSigma_j%5E%7B-1%7D%28x%5E%7B%28i%29%7D-%5Cmu_j%29%29%5Ccdot%5Cphi_j%7D%7Bw_j%5E%7B%28i%29%7D%7D%0A%5Cend%7Baligned%7D%0A&height=147&width=421)

先关于 来进行最大化。如果去关于 的（偏）导数（derivative），得到：

%7Dlog%5Cfrac%7B%5Cfrac%7B1%7D%7B(2%5Cpi)%5E%7Bn%2F2%7D%7C%5CSigmaj%7C%5E%7B1%2F2%7D%7Dexp(-%5Cfrac%2012(x%5E%7B(i)%7D-%5Cmu_j)%5ET%5CSigma_j%5E%7B-1%7D(x%5E%7B(i)%7D-%5Cmu_j))%5Ccdot%5Cphi_j%7D%7Bw_j%5E%7B(i)%7D%7D%20%5C%5C%0A%26%3D%20-%5Cnabla%7B%5Cmul%7D%5Csum%7Bi%3D1%7D%5Em%5Csum%7Bj%3D1%7D%5Ekw_j%5E%7B(i)%7D%5Cfrac%2012(x%5E%7B(i)%7D-%5Cmu_j)%5ET%5CSigma_j%5E%7B-1%7D(x%5E%7B(i)%7D-%5Cmu_j)%20%5C%5C%0A%26%3D%20%5Cfrac%2012%5Csum%7Bi%3D1%7D%5Em%20wl%5E%7B(i)%7D%5Cnabla%7B%5Cmul%7D2%5Cmu_l%5ET%5CSigma_l%5E%7B-1%7Dx%5E%7B(i)%7D-%5Cmu_l%5ET%5CSigma_l%5E%7B-1%7D%5Cmu_l%20%20%5C%5C%0A%26%3D%20%5Csum%7Bi%3D1%7D%5Em%20wl%5E%7B(i)%7D(%5CSigma_l%5E%7B-1%7Dx%5E%7B(i)%7D-%5CSigma_l%5E%7B-1%7D%5Cmu_l)%0A%5Cend%7Baligned%7D%0A#card=math&code=%5Cbegin%7Baligned%7D%0A%5Cnabla%7B%5Cmul%7D%26%5Csum%7Bi%3D1%7D%5Em%5Csum%7Bj%3D1%7D%5Ekw_j%5E%7B%28i%29%7Dlog%5Cfrac%7B%5Cfrac%7B1%7D%7B%282%5Cpi%29%5E%7Bn%2F2%7D%7C%5CSigma_j%7C%5E%7B1%2F2%7D%7Dexp%28-%5Cfrac%2012%28x%5E%7B%28i%29%7D-%5Cmu_j%29%5ET%5CSigma_j%5E%7B-1%7D%28x%5E%7B%28i%29%7D-%5Cmu_j%29%29%5Ccdot%5Cphi_j%7D%7Bw_j%5E%7B%28i%29%7D%7D%20%5C%5C%0A%26%3D%20-%5Cnabla%7B%5Cmul%7D%5Csum%7Bi%3D1%7D%5Em%5Csum%7Bj%3D1%7D%5Ekw_j%5E%7B%28i%29%7D%5Cfrac%2012%28x%5E%7B%28i%29%7D-%5Cmu_j%29%5ET%5CSigma_j%5E%7B-1%7D%28x%5E%7B%28i%29%7D-%5Cmu_j%29%20%5C%5C%0A%26%3D%20%5Cfrac%2012%5Csum%7Bi%3D1%7D%5Em%20wl%5E%7B%28i%29%7D%5Cnabla%7B%5Cmul%7D2%5Cmu_l%5ET%5CSigma_l%5E%7B-1%7Dx%5E%7B%28i%29%7D-%5Cmu_l%5ET%5CSigma_l%5E%7B-1%7D%5Cmu_l%20%20%5C%5C%0A%26%3D%20%5Csum%7Bi%3D1%7D%5Em%20w_l%5E%7B%28i%29%7D%28%5CSigma_l%5E%7B-1%7Dx%5E%7B%28i%29%7D-%5CSigma_l%5E%7B-1%7D%5Cmu_l%29%0A%5Cend%7Baligned%7D%0A&height=183&width=407)

设上式为零，然后解出 就产生了更新规则（update rule）：

%7Dx%5E%7B(i)%7D%7D%7B%5Csum%7Bi%3D1%7D%5Em%20w_l%5E%7B(i)%7D%7D%0A#card=math&code=%5Cmu_l%20%3A%3D%20%5Cfrac%7B%5Csum%7Bi%3D1%7D%5Em%20wl%5E%7B%28i%29%7Dx%5E%7B%28i%29%7D%7D%7B%5Csum%7Bi%3D1%7D%5Em%20w_l%5E%7B%28i%29%7D%7D%0A&height=47&width=114)

这个结果咱们在之前的讲义中已经见到过了。

咱们再举一个例子，推导在 步骤中参数 的更新规则。把仅关于参数 的表达式结合起来，就能发现只需要最大化下面的表达式：

%7Dlog%5Cphij%0A#card=math&code=%5Csum%7Bi%3D1%7D%5Em%5Csum_%7Bj%3D1%7D%5Ekw_j%5E%7B%28i%29%7Dlog%5Cphi_j%0A&height=45&width=95)

然而，还有一个附加的约束，即 的和为，因为其表示的是概率 %7D%20%3D%20j%3B%5Cphi)#card=math&code=%5Cphij%20%3D%20p%28z%5E%7B%28i%29%7D%20%3D%20j%3B%5Cphi%29&height=20&width=105)。为了保证这个约束条件成立，即 ，我们构建一个拉格朗日函数（Lagrangian）：

%3D%5Csum%7Bi%3D1%7D%5Em%5Csum%7Bj%3D1%7D%5Ekwj%5E%7B(i)%7Dlog%5Cphi_j%2B%5Cbeta(%5Csum%5Ek%7Bj%3D1%7D%5Cphij%20-%201)%0A#card=math&code=%5Cmathcal%20L%28%5Cphi%29%3D%5Csum%7Bi%3D1%7D%5Em%5Csum%7Bj%3D1%7D%5Ekw_j%5E%7B%28i%29%7Dlog%5Cphi_j%2B%5Cbeta%28%5Csum%5Ek%7Bj%3D1%7D%5Cphi_j%20-%201%29%0A&height=45&width=235)

其中的 是 拉格朗日乘数（Lagrange multiplier） 。求导，然后得到：

%3D%5Csum%7Bi%3D1%7D%5Em%5Cfrac%7Bw_j%5E%7B(i)%7D%7D%7B%5Cphi_j%7D%2B1%0A#card=math&code=%5Cfrac%7B%5Cpartial%7D%7B%5Cpartial%7B%5Cphi_j%7D%7D%5Cmathcal%20L%28%5Cphi%29%3D%5Csum%7Bi%3D1%7D%5Em%5Cfrac%7Bw_j%5E%7B%28i%29%7D%7D%7B%5Cphi_j%7D%2B1%0A&height=46&width=144)

2 这里我们不用在意约束条件 ，因为很快就能发现，这里推导得到的解会自然满足这个条件的。

设导数为零，然后解方程，就得到了：

%7D%7D%7B-%5Cbeta%7D%0A#card=math&code=%5Cphij%3D%5Cfrac%7B%5Csum%7Bi%3D1%7D%5Em%20w_j%5E%7B%28i%29%7D%7D%7B-%5Cbeta%7D%0A&height=42&width=91)

也就是说，$\phij\propto \sum{i=1}^m wj^{(i)} \Sigma_j \phi_j = 1$，可以很容易地发现 %7D%20%3D%20%5Csum%7Bi%3D1%7D%5Em%201%20%3Dm#card=math&code=-%5Cbeta%20%3D%20%5Csum%7Bi%3D1%7D%5Em%5Csum%7Bj%3D1%7D%5Ekwj%5E%7B%28i%29%7D%20%3D%20%5Csum%7Bi%3D1%7D%5Em%201%20%3Dm&height=45&width=178). （这里用到了条件 %7D%20%3DQ_i(z%5E%7B(i)%7D%20%3D%20j)#card=math&code=w_j%5E%7B%28i%29%7D%20%3DQ_i%28z%5E%7B%28i%29%7D%20%3D%20j%29&height=23&width=107)，而且因为所有概率之和等于，即%7D%3D1#card=math&code=%5Csum_j%20w_j%5E%7B%28i%29%7D%3D1&height=35&width=68)）。这样我们就得到了在 步骤中对参数 进行更新的规则了：

%7D%0A#card=math&code=%5Cphij%20%3A%3D%20%5Cfrac%201m%20%5Csum%7Bi%3D1%7D%5Em%20w_j%5E%7B%28i%29%7D%0A&height=40&width=98)

接下来对 步骤中对 的更新规则的推导就很容易了。