🚀原文地址 📑Notebook

This notebook shows how the SHAP interaction values for a very simple function are computed. We start with a simple linear function, and then add an interaction term to see how it changes the SHAP values and the SHAP interaction values.

  1. import xgboost as xgb
  2. import numpy as np
  3. import shap

1. Explain a linear function with no interactions

  1. # simulate some binary data and a linear outcome with an interaction term
  2. # note we make the features in X perfectly independent of each other to make
  3. # it easy to solve for the exact SHAP values
  4. N = 2000
  5. X = np.zeros((N, 5))
  6. X[:1000, 0] = 1
  7. X[:500, 1] = 1
  8. X[1000:1500, 1] = 1
  9. X[:250, 2] = 1
  10. X[500:750, 2] = 1
  11. X[1000:1250, 2] = 1
  12. X[1500:1750, 2] = 1
  13. X[:, 0:3] -= 0.5
  14. y = 2 * X[:,0] - 3 * X[:, 1]
  16. # ensure the variables are independent
  17. np.cov(X.T)
  19. # and mean centered
  20. X.mean(0)

np.cov 函数用来计算协方差矩阵，如果输入只有一个数组的话，那就是计算方差

  1. # train a model with single tree
  2. Xd = xgb.DMatrix(X, label=y)
  3. model = xgb.train({
  4.     'eta': 1, 
  5.     'max_depth': 3, 
  6.     'base_score': 0, 
  7.     'lambda': 0
  8.     }, Xd, 1)
  9. print("Model error =", np.linalg.norm(y - model.predict(Xd)))
  10. print(model.get_dump(with_stats=True)[0])
  12. # Model error = 0.0
  13. # 0:[f1<0] yes=1,no=2,missing=1,gain=4500,cover=2000
  14. #     1:[f0<0] yes=3,no=4,missing=3,gain=1000,cover=1000
  15. #         3:leaf=0.5,cover=500
  16. #         4:leaf=2.5,cover=500
  17. #     2:[f0<0] yes=5,no=6,missing=5,gain=1000,cover=1000
  18. #         5:leaf=-2.5,cover=500
  19. #         6:leaf=-0.5,cover=500

:::info 解释一下上面代码： ::: :::success

  • XGB 参数中 base_score 表示对于所有样本预测为正样本的全局偏置，如果迭代次数够多，改变这个参数对结果不会有影响。将 base_score 设置为 #(正样本)/#(所有样本) 可减少迭代次数
  • np.linalg.norm 表示对输入数组求范式，默认为 🙈 Basic SHAP Interaction Value Example in XGBoost - 图1，公式：🙈 Basic SHAP Interaction Value Example in XGBoost - 图2
  • model.get_dump 表示查看基分类器的决策树如何选择特征来进行分裂的，with_stats 设置为 True 表示输出分裂统计信息 :::
  1. # make sure the SHAP values add up to marginal predictions
  2. pred = model.predict(Xd, output_margin=True)
  3. explainer = shap.TreeExplainer(model)
  4. shap_values = explainer.shap_values(Xd)
  5. np.abs(shap_values.sum(1) + explainer.expected_value - pred).max()  # 0


:::info 解释一下上面的代码： ::: :::success

  • model.predict 方法中 output_margin 参数，设置为 True 时，输出的不是概率值而是每个样本在 XGB 生成的所有树中叶子节点的累加值
  • explainer.expected_value 为样本期望值 :::

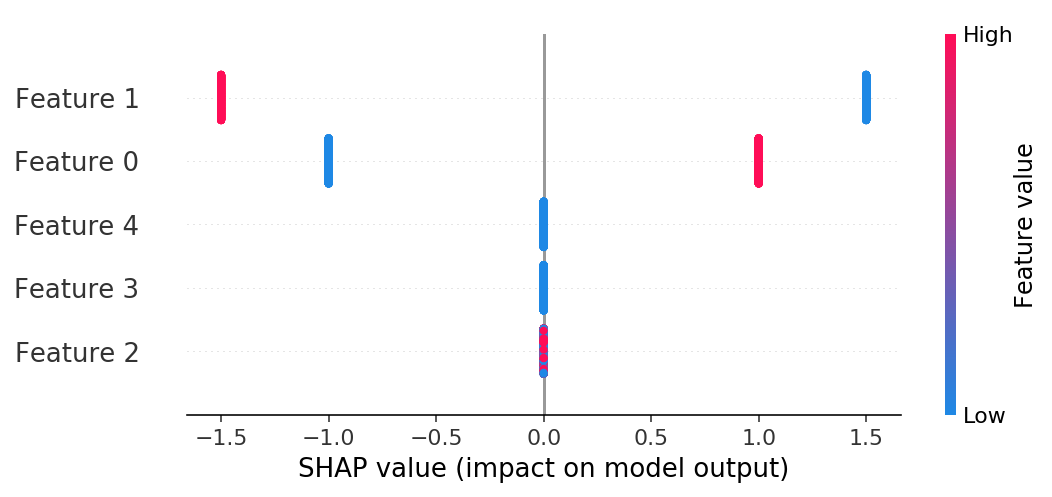
If we build a summary plot we see that only features 1 and 2 have any effect, and that their effects only have two possible magnitudes (one for -0.5 and for 0.5).

  1. shap.summary_plot(shap_values, X)

image.png

  1. # train a linear model
  2. from sklearn import linear_model
  3. lr = linear_model.LinearRegression()
  4. lr.fit(X, y)
  5. lr_pred = lr.predict(X)
  6. lr.coef_.round(2)  # array([ 2., -3.,  0.,  0.,  0.])
  8. # Make sure the computed SHAP values match the true SHAP values
  9. # (we can compute the true SHAP values directly for this simple case)
  10. main_effect_shap_values = lr.coef_ * (X - X.mean(0))
  11. np.linalg.norm(shap_values - main_effect_shap_values)  # 1.654243349044798e-13

1.1 SHAP Interaction Values

Note that when there are no interactions present the SHAP interaction values are just a diagonal matrix with the SHAP values on the diagonal(对角线).

  1. shap_interaction_values = explainer.shap_interaction_values(Xd)
  2. shap_interaction_values[0]
  3. # array([[ 1. ,  0. ,  0. ,  0. ,  0. ],
  4. #        [ 0. , -1.5,  0. ,  0. ,  0. ],
  5. #        [ 0. ,  0. ,  0. ,  0. ,  0. ],
  6. #        [ 0. ,  0. ,  0. ,  0. ,  0. ],
  7. #        [ 0. ,  0. ,  0. ,  0. ,  0. ]], dtype=float32)
  9. # ensure the SHAP interaction values sum to the marginal predictions
  10. np.abs(shap_interaction_values.sum((1, 2)) + explainer.expected_value - pred).max()  # 0
  12. # ensure the main effects from the SHAP interaction values match those from a linear model
  13. dinds = np.diag_indices(shap_interaction_values.shape[1])
  14. total = 0
  16. for i in range(N):
  17.     for j in range(5):
  18.         total += np.abs(shap_interaction_values[i, j, j] - main_effect_shap_values[i, j])
  20. total  # 1.0533118387982904e-11

:::info 解释： ::: :::success

  • np.diag_indices 返回一组索引，用来访问 N x N 数组的对角线 :::

    2. Explain a linear model with one interaction

    ```python

    simulate some binary data and a linear outcome with an interaction term

    note we make the features in X perfectly independent of each other to make

    it easy to solve for the exact SHAP values

    N = 2000 X = np.zeros((N, 5)) X[:1000, 0] = 1

X[:500, 1] = 1 X[1000:1500, 1] = 1

X[:250, 2] = 1 X[500:750, 2] = 1 X[1000:1250, 2] = 1 X[1500:1750, 2] = 1

X[:125, 3] = 1 X[250:375, 3] = 1 X[500:625, 3] = 1 X[750:875, 3] = 1 X[1000:1125, 3] = 1 X[1250:1375, 3] = 1 X[1500:1625, 3] = 1 X[1750:1875, 3] = 1 X[:,:4] -= 0.4999 # we can’t exactly mean center the data or XGBoost has trouble finding the splits y = 2 X[:, 0] - 3 X[:, 1] + 2 X[:, 1] X[:, 2]

X.mean(0) # array([1.e-04, 1.e-04, 1.e-04, 1.e-04, 0.e+00])

train a model with single tree

Xd = xgb.DMatrix(X, label=y) model = xgb.train({‘eta’: 1, ‘max_depth’: 4, ‘base_score’: 0, “lambda”: 0}, Xd, 1) print(“Model error =”, np.linalg.norm(y-model.predict(Xd))) print(model.get_dump(with_stats=True)[0])

make sure the SHAP values add up to marginal predictions

pred = model.predict(Xd, output_margin=True) explainer = shap.TreeExplainer(model) shap_values = explainer.shap_values(Xd) np.abs(shap_values.sum(1) + explainer.expected_value - pred).max() # 4.7683716e-07

  1. 输出结果：

Model error = 1.7365037830677591e-06 0:[f1<0.000100001693] yes=1,no=2,missing=1,gain=4499.40039,cover=2000 1:[f0<0.000100001693] yes=3,no=4,missing=3,gain=999.999756,cover=1000 3:[f2<0.000100001693] yes=7,no=8,missing=7,gain=124.949997,cover=500 7:leaf=0.99970001,cover=250 8:leaf=-9.99800031e-05,cover=250 4:[f2<0.000100001693] yes=9,no=10,missing=9,gain=124.949951,cover=500 9:leaf=2.99970007,cover=250 10:leaf=1.99989998,cover=250 2:[f0<0.000100001693] yes=5,no=6,missing=5,gain=999.999756,cover=1000 5:[f2<0.000100001693] yes=11,no=12,missing=11,gain=125.050049,cover=500 11:leaf=-3.0000999,cover=250 12:leaf=-1.99989998,cover=250 6:[f2<0.000100001693] yes=13,no=14,missing=13,gain=125.050018,cover=500 13:leaf=-1.00010002,cover=250 14:leaf=0.000100019999,cover=250

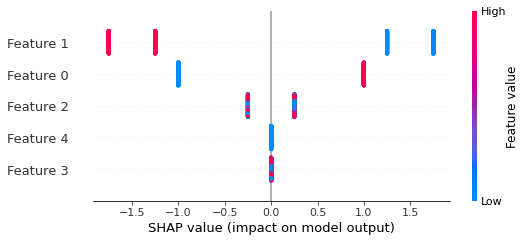
  1. If we build a summary plot we see that now only features 3 and 4 don't matter, and that feature 1 can have four possible effect sizes due to interactions.
  2. ```python
  3. shap.summary_plot(shap_values, X)

image.png

  1. # train a linear model
  2. lr = linear_model.LinearRegression()
  3. lr.fit(X, y)
  4. lr_pred = lr.predict(X)
  5. lr.coef_.round(2)  # array([ 2., -3.,  0.,  0.,  0.])
  7. # Note that the SHAP values no longer match the main effects because they now include interaction effects
  8. main_effect_shap_values = lr.coef_ * (X - X.mean(0))
  9. np.linalg.norm(shap_values - main_effect_shap_values)  # 15.811389093449788

2.1 SHAP interaction values

  1. # SHAP interaction contributions:
  2. shap_interaction_values = explainer.shap_interaction_values(Xd)
  3. shap_interaction_values[0].round(2)
  4. # Output:
  5. # array([[ 1.  ,  0.  ,  0.  ,  0.  ,  0.  ],
  6. #        [ 0.  , -1.5 ,  0.25,  0.  ,  0.  ],
  7. #        [ 0.  ,  0.25,  0.  ,  0.  ,  0.  ],
  8. #        [ 0.  ,  0.  ,  0.  ,  0.  ,  0.  ],
  9. #        [ 0.  ,  0.  ,  0.  ,  0.  ,  0.  ]], dtype=float32)
  12. # ensure the SHAP interaction values sum to the marginal predictions
  13. np.abs(shap_interaction_values.sum((1, 2)) + explainer.expected_value - pred).max()
  14. # Output: 4.7683716e-07
  16. # ensure the main effects from the SHAP interaction values match those from a linear model.
  17. # while the main effects no longer match the SHAP values when interactions are present, they do match
  18. # the main effects on the diagonal of the SHAP interaction value matrix
  19. dinds = np.diag_indices(shap_interaction_values.shape[1])
  20. total = 0
  22. for i in range(N):
  23.     for j in range(5):
  24.         total += np.abs(shap_interaction_values[i, j, j] - main_effect_shap_values[i, j])
  25. total  # 0.4000067711135082

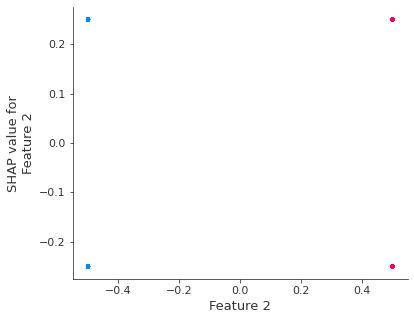
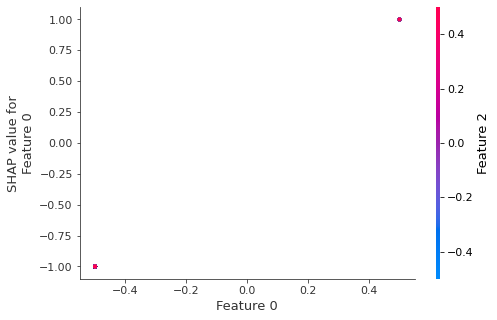
If we build a dependence plot for feature 0 we that it only takes two values and that these values are entirely dependent on the value of the feature (the value of feature 0 entirely determines it’s effect because it has no interactions with other features).

  1. shap.dependence_plot(0, shap_values, X)

image.png
In contrast if we build a dependence plot for feature 2 we see that it takes 4 possible values and they are not entirely determined by the value of feature 2, instead they also depend on the value of feature 3. This vertical spread in a dependence plot represents the effects of non-linear interactions.

  1. shap.dependence_plot(2, shap_values, X)

image.png