🚀 原文链接：https://xgboost.readthedocs.io/en/latest/tutorials/model.html

XGBoost stands for(代表 ) “Extreme Gradient Boosting”, where the term “Gradient Boosting” originates(起源于) from the paper Greedy Function Approximation: A Gradient Boosting Machine, by Friedman.

The gradient boosted trees has been around for a while, and there are a lot of materials on the topic. This tutorial will explain boosted trees in a self-contained(self-contained：独立的) and principled way using the elements of supervised learning. We think this explanation is cleaner, more formal(正式的), and motivates(说明…的原因) the model formulation used in XGBoost.

1、Elements of Supervised Learning

XGBoost is used for supervised learning problems, where we use the training data (with multiple features) to predict a target variable . Before we learn about trees specifically, let us start by reviewing the basic elements in supervised learning.

1.1 Model and Parameters

The model in supervised learning usually refers to the mathematical structure of by which the prediction is made from the input . A common example is a linear model, where the prediction is given as , a linear combination of weighted input features. The prediction value can have different interpretations(解释), depending on the task, i.e., regression or classification. For example, it can be logistic transformed to get the probability of positive class in logistic regression, and it can also be used as a ranking score when we want to rank the outputs.

The parameters are the undetermined(未确定的) part that we need to learn from data. In linear regression problems, the parameters are the coefficients θ. Usually we will use θ to denote(表示 ) the parameters (there are many parameters in a model, our definition here is sloppy(草率的)).

1.2 Objective Function: Training Loss + Regularization

With judicious(明智的) choices for , we may express a variety of tasks, such as regression, classification, and ranking. The task of training the model amounts to finding the best parameters θ that best fit the training data and labels . In order to train the model, we need to define the objective function to measure how well the model fit the training data.

A salient(显著的) characteristic of objective functions is that they consist two parts: training loss and regularization term:

where is the training loss function, and is the regularization term. The training loss measures how predictive our model is with respect to(关于) the training data. A common choice of is the mean squared error, which is given by

Another commonly used loss function is logistic loss, to be used for logistic regression:

The regularization term is what people usually forget to add. The regularization term controls the complexity of the model, which helps us to avoid overfitting. This sounds a bit abstract, so let us consider the following problem in the following picture. You are asked to fit visually a step function given the input data points on the upper left corner of the image. Which solution among the three do you think is the best fit?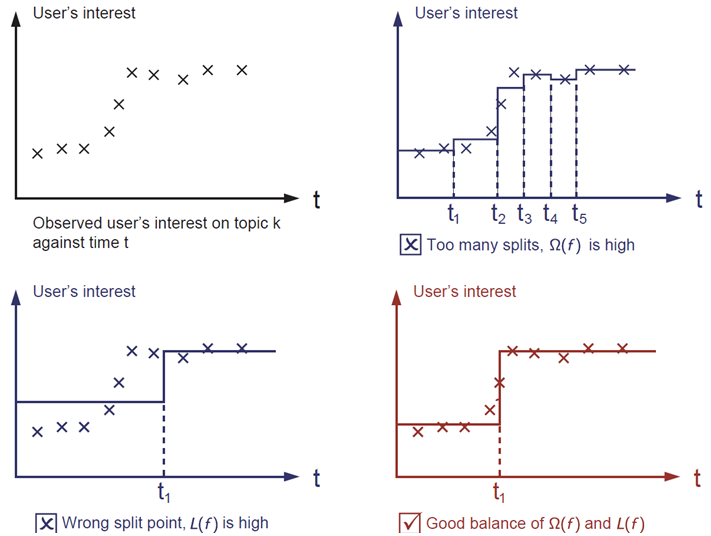

The correct answer is marked in red. Please consider if this visually seems a reasonable fit to you. The general principle is we want both a simple and predictive model. The tradeoff(折中，平衡) between the two is also referred as bias-variance tradeoff in machine learning.

1.3 Why introduce the general principle?

The elements introduced above form the basic elements of supervised learning, and they are natural building blocks of machine learning toolkits(工具包 ). For example, you should be able to describe the differences and commonalities(共同特征) between gradient boosted trees and random forests. Understanding the process in a formalized(使定形 ) way also helps us to understand the objective that we are learning and the reason behind the heuristics(启发) such as pruning(剪枝) and smoothing(平滑). :::info 上述内容有一个单词 smoothing，意为平滑，在树模型中这个概念很少被提及。相同的概念我们在 Scikit-Learn GradientBoostingRegressor 文档中也提及到了：

借助上面 4 张图，来解释下 smoothing 概念：

• 当我们目标函数是像第 2 张图（第 1 行第 2 张）,由于叶子节点样本数量没有做限制，所以你会看到目标函数呈现阶梯状，且非常不平滑
• 当我们限制了每个叶子节点上最小的样本量，这样目标函数将会类似于第 3、4 张图，变得比较平滑。 :::

  min_samples_leafint or float, default=1 The minimum number of samples required to be at a leaf node. A split point at any depth will only be considered if it leaves at least min_samples_leaf training samples in each of the left and right branches. This may have the effect of smoothing the model, especially in regression.

2、Decision Tree Ensembles

Now that we have introduced the elements of supervised learning, let us get started with real trees. To begin with, let us first learn about the model choice of XGBoost: decision tree ensembles. The tree ensemble(集成) model consists of a set of classification and regression trees (CART). Here’s a simple example of a CART that classifies whether someone will like a hypothetical(假设的) computer game X.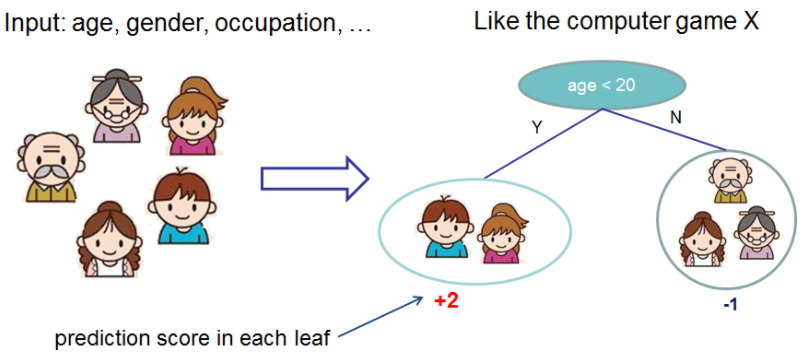

We classify the members of a family into different leaves, and assign them the score on the corresponding leaf. A CART is a bit different from decision trees, in which the leaf only contains decision values. In CART, a real score is associated with each of the leaves, which gives us richer interpretations(解释) that go beyond classification. This also allows for a principled, unified(统一的) approach to optimization, as we will see in a later part of this tutorial.

Usually, a single tree is not strong enough to be used in practice. What is actually used is the ensemble model, which sums the prediction of multiple trees together.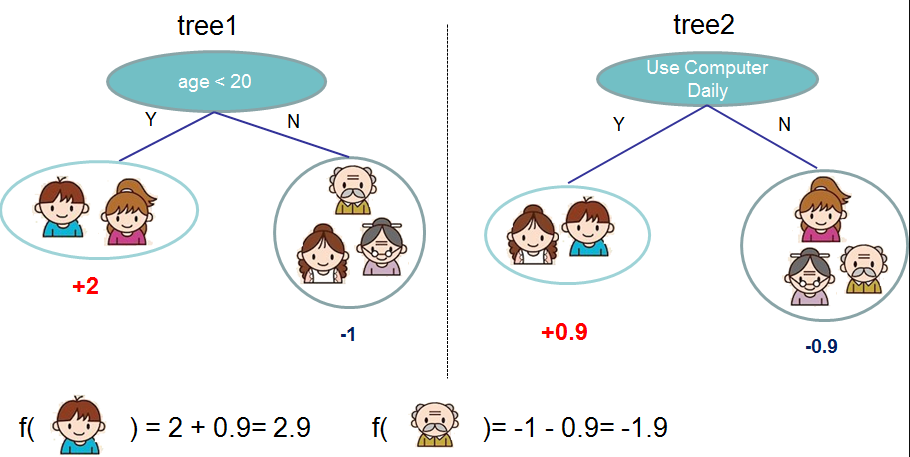
:::warning ❓ 这里 +2、-1、+0.9 以及 -0.9 含义并不清楚，可以先理解为倾向值。 :::

Here is an example of a tree ensemble of two trees. The prediction scores of each individual tree are summed up to get the final score. If you look at the example, an important fact is that the two trees try to complement(补充) each other. Mathematically, we can write our model in the form

where is the number of trees, is a function in the functional space , and is the set of all possible CARTs. The objective function to be optimized is given by

Now here comes a trick question: what is the model used in random forests? Tree ensembles! So random forests and boosted trees are really the same models; the difference arises from(来自) how we train them. This means that, if you write a predictive service for tree ensembles, you only need to write one and it should work for both random forests and gradient boosted trees. (See Treelite for an actual example.) One example of why elements of supervised learning rock(变化).

3、Tree Boosting

Now that we introduced the model, let us turn to training: How should we learn the trees? The answer is, as is always for(都是如此) all supervised learning models: define an objective function and optimize it!

Let the following be the objective function (remember it always needs to contain training loss and regularization):

3.1 Additive Training

The first question we want to ask: what are the parameters of trees? You can find that what we need to learn are those functions , each containing the structure of the tree and the leaf scores. Learning tree structure is much harder than traditional optimization problem where you can simply take the gradient. It is intractable(棘手的) to learn all the trees at once. Instead, we use an additive(加速的) strategy: fix what we have learned, and add one new tree at a time. We write the prediction value at step as . Then we have

It remains to ask: which tree do we want at each step? A natural thing is to add the one that optimizes our objective.

If we consider using mean squared error (MSE) as our loss function, the objective becomes

The form(形式) of MSE is friendly, with a first order(一阶导) term (usually called the residual(残差)) and a quadratic term(平方项). For other losses of interest (for example, logistic loss), it is not so easy to get such a nice form. So c, we take the Taylor expansion of the loss function up to the second order(二阶):

where the and are defined as

After we remove all the constants, the specific objective at step becomes

❓ 为什么直接去掉了 项，是为 0 么

This becomes our optimization goal for the new tree. One important advantage of this definition is that the value of the objective function only depends on and . This is how XGBoost supports custom loss functions. We can optimize every loss function, including logistic regression and pairwise ranking(两两排名), using exactly the same solver(求解器) that takes and as input!

3.2 Model Complexity

We have introduced the training step, but wait, there is one important thing, the regularization term! We need to define the complexity of the tree . In order to do so, let us first refine the definition of the tree as

Here is the vector of scores on leaves, is a function assigning each data point to the corresponding leaf, and is the number of leaves. In XGBoost, we define the complexity as

Of course, there is more than one way to define the complexity, but this one works well in practice. The regularization is one part most tree packages treat less carefully, or simply ignore. This was because the traditional treatment of tree learning only emphasized improving impurity(不纯度), while the complexity control was left to heuristics. By defining it formally, we can get a better idea of what we are learning and obtain models that perform well in the wild(自然地).

3.3 The Structure Score

Here is the magical part of the derivation(由来). After re-formulating(重新制定) the tree model, we can write the objective value with the -th tree as:

where is the set of indices(索引) of data points assigned to the -th leaf. Notice that in the second line we have changed the index of the summation(总结) because all the data points on the same leaf get the same score. We could further compress the expression by defining and :

In this equation, are independent with respect to(关于) each other, the form is quadratic and the best for a given structure and the best objective reduction we can get is:

The last equation measures how good a tree structure is.

If all this sounds a bit complicated, let’s take a look at the picture, and see how the scores can be calculated. Basically, for a given tree structure, we push the statistics and to the leaves they belong to, sum the statistics together, and use the formula to calculate how good the tree is. This score is like the impurity measure in a decision tree, except that it also takes the model complexity into account.

3.4 Learn the tree structure

Now that we have a way to measure how good a tree is, ideally we would enumerate all possible trees and pick the best one. In practice this is intractable, so we will try to optimize one level of the tree at a time. Specifically we try to split a leaf into two leaves, and the score it gains is

This formula can be decomposed as
1) the score on the new left leaf
2) the score on the new right leaf
3) The score on the original leaf
4) regularization on the additional leaf.
We can see an important fact here: if the gain is smaller than , we would do better not to add that branch. This is exactly the pruning techniques in tree based models! By using the principles of supervised learning, we can naturally come up with(想出) the reason these techniques work.

For real valued data, we usually want to search for an optimal split. To efficiently do so, we place all the instances in sorted order, like the following picture.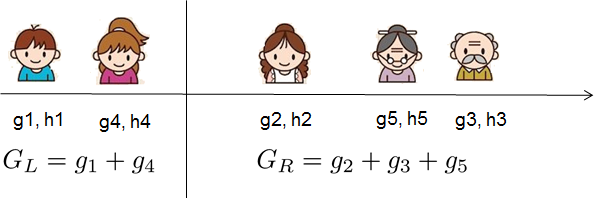

A left to right scan is sufficient(足够的) to calculate the structure score of all possible split solutions, and we can find the best split efficiently.

:::tips 🔖 Note ::: :::info Limitation of additive tree learning
Since it is intractable to enumerate all possible tree structures, we add one split at a time. This approach works well most of the time, but there are some edge cases that fail due to this approach. For those edge cases, training results in a degenerate(退化) model because we consider only one feature dimension at a time. See Can Gradient Boosting Learn Simple Arithmetic? for an example. :::

4、Final words on XGBoost

Now that you understand what boosted trees are, you may ask, where is the introduction for XGBoost? XGBoost is exactly a tool motivated by the formal principle introduced in this tutorial! More importantly, it is developed with both deep consideration in terms of systems optimization and principles in machine learning. The goal of this library is to push the extreme(极大的) of the computation limits of machines to provide a scalable, portable and accurate library. Make sure you try it out, and most importantly, contribute your piece of wisdom (code, examples, tutorials) to the community!