试了试前三种方法，一个一秒一帧一个5秒一帧，只有cv2.Laplacian能跟得上摄像头的连续出图，后面的看了下似乎也都是需要各种高强度计算，懒得测试了
主要：

  1. while (cv2.waitKey(1) != 27):
  2.         print(cv2.Laplacian(mat,cv2.CV_64F).var())#mat:灰度图，返回的值越大图像越清晰对焦越准确
  3.         cv2.imshow(u"Camera", mat)#显示图像数据

用的摄像头用OpenCV打不开，只能用厂家提供的SDK，代码肯定不能和其他摄像头通用，用的黑白摄像头，彩色的话要先把图像转换成灰度图

  1. import numpy as np
  2. import cv2
  3. import math
  5. from dvp import *
  7. def frame2mat(frameBuffer):
  8.     frame, buffer = frameBuffer
  9.     bits = np.uint8 if(frame.bits == Bits.BITS_8) else np.uint16
  10.     shape = None
  11.     convertType = None
  12.     if(frame.format >= ImageFormat.FORMAT_MONO and frame.format <= ImageFormat.FORMAT_BAYER_RG):
  13.         shape = 1
  14.     elif(frame.format == ImageFormat.FORMAT_BGR24 or frame.format == ImageFormat.FORMAT_RGB24):
  15.         shape = 3
  16.     elif(frame.format == ImageFormat.FORMAT_BGR32 or frame.format == ImageFormat.FORMAT_RGB32):
  17.         shape = 4
  18.     else:
  19.         return None
  21.     mat = np.frombuffer(buffer, bits)
  22.     mat = mat.reshape(frame.iHeight, frame.iWidth, shape)   #转换维度
  23.     return mat
  25. def brenner(img):
  26.     '''
  27.     Brenner 梯度函数
  28.     :param img:narray 二维灰度图像
  29.     :return: float 图像约清晰越大
  30.     1FPS
  31.     '''
  32.     shape = np.shape(img)
  33.     out = 0
  34.     for x in range(0, shape[0]-2):
  35.         for y in range(0, shape[1]):
  36.             out+=(int(img[x+2,y])-int(img[x,y]))**2
  37.     return out
  39. def Laplacian(img):
  40.     '''
  41.     Laplacian梯度函数
  42.     :param img:narray 二维灰度图像
  43.     :return: float 图像约清晰越大
  44.     30FPS
  45.     '''
  46.     return cv2.Laplacian(img,cv2.CV_64F).var()
  48. def SMD(img):
  49.     '''
  50.     SMD（灰度方差）
  51.     :param img:narray 二维灰度图像
  52.     :return: float 图像约清晰越大
  53.     0.2FPS
  54.     '''
  55.     shape = np.shape(img)
  56.     out = 0
  57.     for x in range(0, shape[0]-1):
  58.         for y in range(1, shape[1]):
  59.             out+=math.fabs(int(img[x,y])-int(img[x,y-1]))
  60.             out+=math.fabs(int(img[x,y]-int(img[x+1,y])))
  61.     return out
  63. camera = Camera(0)#以索引号的方式打开相机
  64. camera.Start()#启动视频流
  66. cv2.namedWindow(u"Camera",0)#可以拖动窗口大小
  67. cv2.resizeWindow(u"Camera", 640, 480)#设置窗口大小
  68. cv2.moveWindow(u"Camera",1200,500)#设置窗口位置
  70. while (cv2.waitKey(1) != 27):
  71.         frame = camera.GetFrame(3000)#从相机采集图像数据，超时时间为3000毫秒
  72.         mat = frame2mat(frame)#转换为标准数据格式
  73.         print(Laplacian(mat))
  74.         cv2.imshow(u"Camera", mat)#显示图像数据

试了下效果，Laplacian对常规场景的判断对焦和失焦的值差距不是很大，对上焦是80左右的数值，失焦也就60左右
但对电子屏幕似乎有奇效，朝着电脑屏幕对上焦后数值能飙到800多
对准焦距：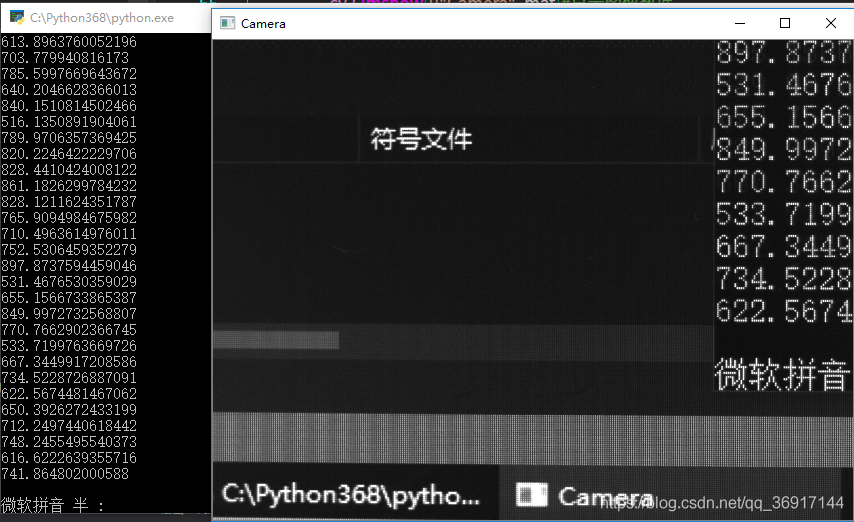
image.png
焦距过长：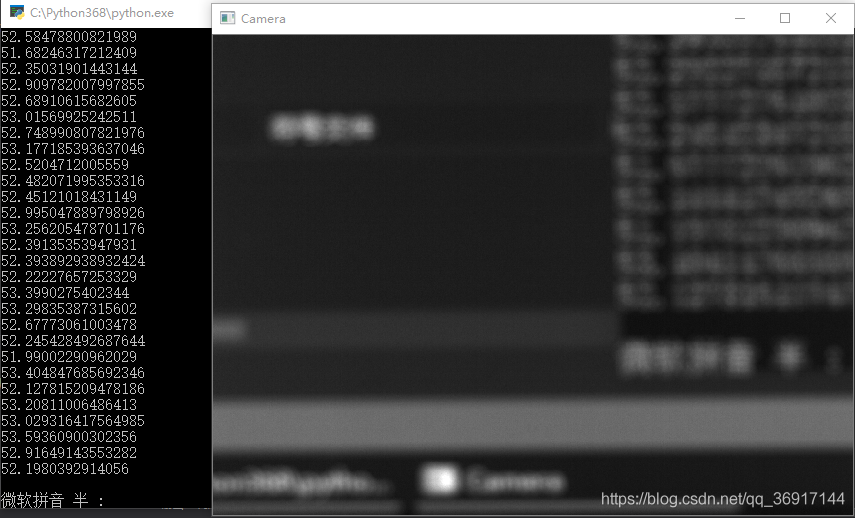
image.png
焦距过短：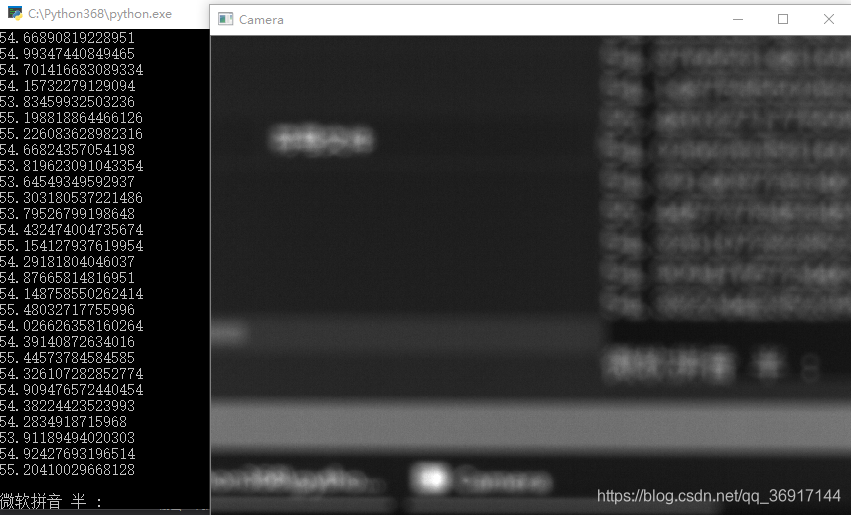
image.png

无参考图像的清晰度评价方法（代码实现Python）

1 Brenner 梯度函数

  1. def brenner(img):
  2.     '''
  3.     :param img:narray 二维灰度图像
  4.     :return: float 图像约清晰越大
  5.     '''
  6.     shape = np.shape(img)
  7.     out = 0
  8.     for x in range(0, shape[0]-2):
  9.         for y in range(0, shape[1]):
  10.             out+=(int(img[x+2,y])-int(img[x,y]))**2
  11.     return out

2 Laplacian梯度函数

  1. def Laplacian(img):
  2.     '''
  3.     :param img:narray 二维灰度图像
  4.     :return: float 图像约清晰越大
  5.     '''
  6.     return cv2.Laplacian(img,cv2.CV_64F).var()

3 SMD（灰度方差）

  1. def SMD(img):
  2.     '''
  3.     :param img:narray 二维灰度图像
  4.     :return: float 图像约清晰越大
  5.     '''
  6.     shape = np.shape(img)
  7.     out = 0
  8.     for x in range(0, shape[0]-1):
  9.         for y in range(1, shape[1]):
  10.             out+=math.fabs(int(img[x,y])-int(img[x,y-1]))
  11.             out+=math.fabs(int(img[x,y]-int(img[x+1,y])))
  12.     return out

4 SMD2（灰度方差乘积）

  1. def SMD2(img):
  2.     '''
  3.     :param img:narray 二维灰度图像
  4.     :return: float 图像约清晰越大
  5.     '''
  6.     shape = np.shape(img)
  7.     out = 0
  8.     for x in range(0, shape[0]-1):
  9.         for y in range(0, shape[1]-1):
  10.             out+=math.fabs(int(img[x,y])-int(img[x+1,y]))*math.fabs(int(img[x,y]-int(img[x,y+1])))
  11.     return out

5 方差函数

  1. def variance(img):
  2.     '''
  3.     :param img:narray 二维灰度图像
  4.     :return: float 图像约清晰越大
  5.     '''
  6.     out = 0
  7.     u = np.mean(img)
  8.     shape = np.shape(img)
  9.     for x in range(0,shape[0]):
  10.         for y in range(0,shape[1]):
  11.             out+=(img[x,y]-u)**2
  12.     return out

6 能量梯度函数

  1. def energy(img):
  2.     '''
  3.     :param img:narray 二维灰度图像
  4.     :return: float 图像约清晰越大
  5.     '''
  6.     shape = np.shape(img)
  7.     out = 0
  8.     for x in range(0, shape[0]-1):
  9.         for y in range(0, shape[1]-1):
  10.             out+=((int(img[x+1,y])-int(img[x,y]))**2)+((int(img[x,y+1]-int(img[x,y])))**2)
  11.     return out

7 Vollath函数

  1. def Vollath(img):
  2.     '''
  3.     :param img:narray 二维灰度图像
  4.     :return: float 图像约清晰越大
  5.     '''
  6.     shape = np.shape(img)
  7.     u = np.mean(img)
  8.     out = -shape[0]*shape[1]*(u**2)
  9.     for x in range(0, shape[0]-1):
  10.         for y in range(0, shape[1]):
  11.             out+=int(img[x,y])*int(img[x+1,y])
  12.     return out

8 熵函数

  1. def entropy(img):
  2.     '''
  3.     :param img:narray 二维灰度图像
  4.     :return: float 图像约清晰越大
  5.     '''
  6.     out = 0
  7.     count = np.shape(img)[0]*np.shape(img)[1]
  8.     p = np.bincount(np.array(img).flatten())
  9.     for i in range(0, len(p)):
  10.         if p[i]!=0:
  11.             out-=p[i]*math.log(p[i]/count)/count
  12.     return out

ref
https://blog.csdn.net/gaoyi221119/article/details/103782288