图像配准

背景及意义

自从相机出现以来，图像获取与图像处理技术就成为绕不开的研究点，随着技术的进步和生产生活的需要，单个摄像机定点采集的图像和视频越来越满足不了人们的需求，追求相机更宽广的视角，一张图像显示更多的信息，这个时候全景图像和视频就应运而生。为获得全景图像/视频目前主流的有两种途径，其一为使用广角镜头进行拍摄，但这种方式缺点也很明显即需要更新换代采集图像的硬件系统而且使用这种镜头拍摄到的图像和视频带有明显的畸变。另一种是在算法层面采用多幅图像拼接的方法实现全景的图像/视频。

研究历程

图像配准现阶段的研究从相关性描述方式方面主要分为基于像素、基于特征和基于频域三种方法。

基于像素的图像配准

基于像素的配准方法是在像素层面进行处理，通常是图像的灰度信息结合模板匹配的方式。1971年Leese[1]提出“MAD”（平均绝对差）算法是比较经典的基于像素的匹配算法，此类算法采用一种或多种相似度测量算法，例如归－化互相关、平方差、均方差等。此方法在图像上设置“滑动窗口”，通过在图像上移动“窗口”并衡量“窗口”中像素的匹配数量（相似性度量）来进行图像间的匹配。基于像素的方法主要有平均绝对差法、归一化积相关算法、基于互信息等。这类算法具有原理简单、运算量大（耗时）、要求图像重叠区域的面积足够多等特点，由于比较的是“窗口”中的像素相关性，所以对于图像存在放缩、变形、遮挡或旋转等都没有很好的适应能力，因此只能用于处理形状大小角度相差不多的图像间的配准。又因为其具有计算方法简单易于实现的优势，所以该算法曾经被广泛运用在同一传感器系统中（图像差异小）。

基于特征的图像配准

基于特征的图像配准方法是从待配准图像中提取某些特征，将这些特征作为处理单元进行相应的描述并依据匹配的情况，计算出待匹配图像间的几何变换参数，从而实现图像间的配准。
图像的特征包括角点、线条、轮廓、纹理或其他特殊结构等，目前主流的特征配准方法依据特征的大小将其分为点特征、边缘特征和区域特征。
Moravec[2]在 1977 年提出了角点检测的概念，由此开启了对图像特征点的检测及配准的研究工作，不过，由于Moravec提出的角点（特征点）检测算子不具备旋转不变性，并且对图像中的边缘点和包含的噪声非常敏感，因此配准的效果并不太理想。1988年 Harris和Stephens[3]提出了Harris检测算子，该特征检测算子与Moravec提出的算法相比较具有了更好的性能，其检测结果具有了良好的检测率和重复率，并且对旋转不变性和灰度变化的不变性也都有较好的适应性。1997 年 Smith 和Bradty[4]提出了另一种基于特征的检测算子——SUSAN 算子，该算子是一种局部检测算子，优点在于对噪声干扰有很好的抵抗能力。在所有对特征点检测的算子中，1999年 Lowe[5]提出的并于2004年完善的尺度不变特征变换（Scale Invariant Feature Transform，SIFT）有着深远的意义。基于SIFT的图像配准方法具有了旋转不变性，尺度不变性和仿射不变性等诸多的优点，尤其适用于高分辨率图像或存在旋转、伸缩或仿射等变换的场景。但该算法也存在着巨大的缺陷即算法复杂度较高使其运算量大，在实际应用中的实时性差，不能满足现代生产生活快节奏的要求，后续很多人针对这样的情况进行了大量的优化和改进工作，2006年Bay[6]等人提出了SURF算法,该算法的性能接近于SIFT算法，在亮度变化和模糊方面均优于SIFT算法，但尺度和旋转的变化不及SIFT。在速度方面，SURF大致上是SIFT算法速度的3倍。但这个速度在我们处理视频信息时仍显得不足。Edward Rosten[7]和Tom Drummond在2006年提出并于2010年优化的FAST算法极大的提高了特征检测的速度，常被用于实时图像处理，但FSAT算法对角度变化的鲁棒性不够。既要满足图像匹配速度的要求又要适应各类复杂场景，于是近年来研究人员提出了新的基于二进制串的局部特征描述子。 2010年Colonder[8]等人提出了BRIEF描述子，通过改用随机响应来替代梯度直方图方法来描述特征点，在很大程度上提高了特征点描述和匹配速度，但是缺点是对噪声敏感且不具备尺度不变性。2011年Rublee[9]等人提出了ORB描述子，该算法运算速度快，具备一定的尺度不变性，但当图像发生尺度变化时，特征点匹配的准确率会有所下滑。同年Leutenegger[10]等人提出了BRISK描述子，该描述子算法具备尺度和角度的不变性，且运算速度快，尤其是在处理有较大模糊的图像时表现出优越的性能。2012年Alahi[11]等提出了FREAK描述子，通过模拟人类视网膜的特性来进行特征检测与描述，具有稳定的性能，但缺点是当图像场景存在大小尺度差异时，特征点的匹配准确率较低。最近几年，国内的研究学者也对图像配准进行了大量的工作。2016年徐振宇[12]等人提出了一种八边形滤波器检测和描述特征的方法DFOB，此方法的优点是不用对图像进行预处理，速度很快且性能稳定。2016年苗正伟[13]等提出了一种零模LOG滤波器进行对比度不变的兴趣点检测，此方法解决了传统二进制描述子对噪声敏感的问题，具有更快的速度和更好的鲁棒性。
除了点特征以外，目前也有了许多对图像边缘进行检测的算法，并且大多都非常成熟，检测效率也很高。经典的图像边缘检测算法有直方图法，梯度算子、Canny[14] [15]算子、Hough [16]变换等，其中，梯度算子里面包含了很多种类，例如，Roberts 算子、Sobel 算子、Prewitt [17]算子等。其中，Canny 算子是目前边缘检测中非常有效的算子，也有很多基于 Canny 算子的改进算子被陆续提了出来，但这类 Canny 算子都有一个缺点，对图像中弱边缘的检测并没有十分地有效。Hough 变换也是一种非常常用的算子，一般会使用 Hough 变换和其他的边缘检测算子组合来检测和连接图像中的线段。基于区域特征的图像配准方法着力于提取高层次的特征进行匹配，这些高层次的特征更容易被人类感知理解，更贴近于人的认知，包括形状和纹理。形状特征通过位置、方向、大小或者相互间结构描述，这些特征匹配不仅用于寻找相关性而且进一步用于变换参数的计算。Prescott[18]采用高层次特征阈值约束和计算基于区域相似特征的方法完成了图像的匹配。但使用高层次特征进行配准会增大计算复杂度，在当前运算速度下只适用于在大场景、具有复杂目标位移参数或是多层次图像拼接的时候。

基于频域的图像配准

基于频域的图像配准方法利用图像频域信息进行最优变换参数的计算，从原理上说便是利用图像经傅里叶变换后图像平移、旋转、缩放在频域上具有对称性。现阶段对于图像的平移一般采用相位相关法，较为成熟的方法是使用两幅待配准图像互功率谱中的相位脉冲函数来进行图像配准。基于频域的图像配准算法因为采用傅里叶变换的位移性质和快速傅里叶变换具有效率高的优点，但是对于噪声敏感。基于频域的方法不仅局限于图像平移的估计，采用对数极坐标变换估计尺度和位移的参数；对于图像间时存在平移、旋转和缩放时使用傅里叶梅林变换改变位移参数中的旋转和缩放参数，这种方式可以在配准过程中利用图像的全部信息内容，克服相关性噪音和频率噪声，能大大减小几何失真的影响。

基于特征点的图像配准

在介绍特征点发之前先简要介绍一下基于灰度信息的方法：

基于特征点的图像配准流程主要有四步：特征提取、特征匹配、参数估计、图形变换。
1.特征提取：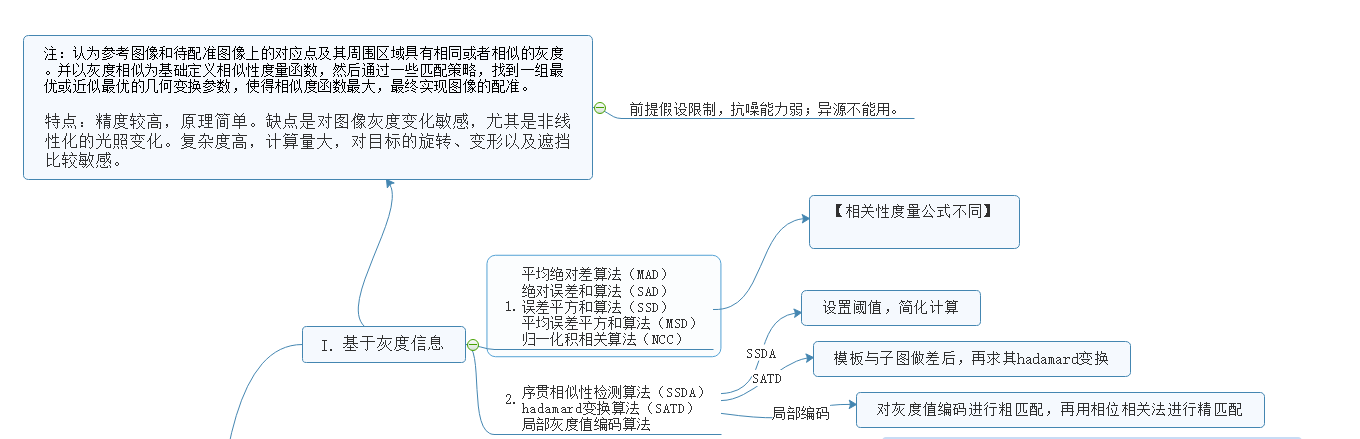


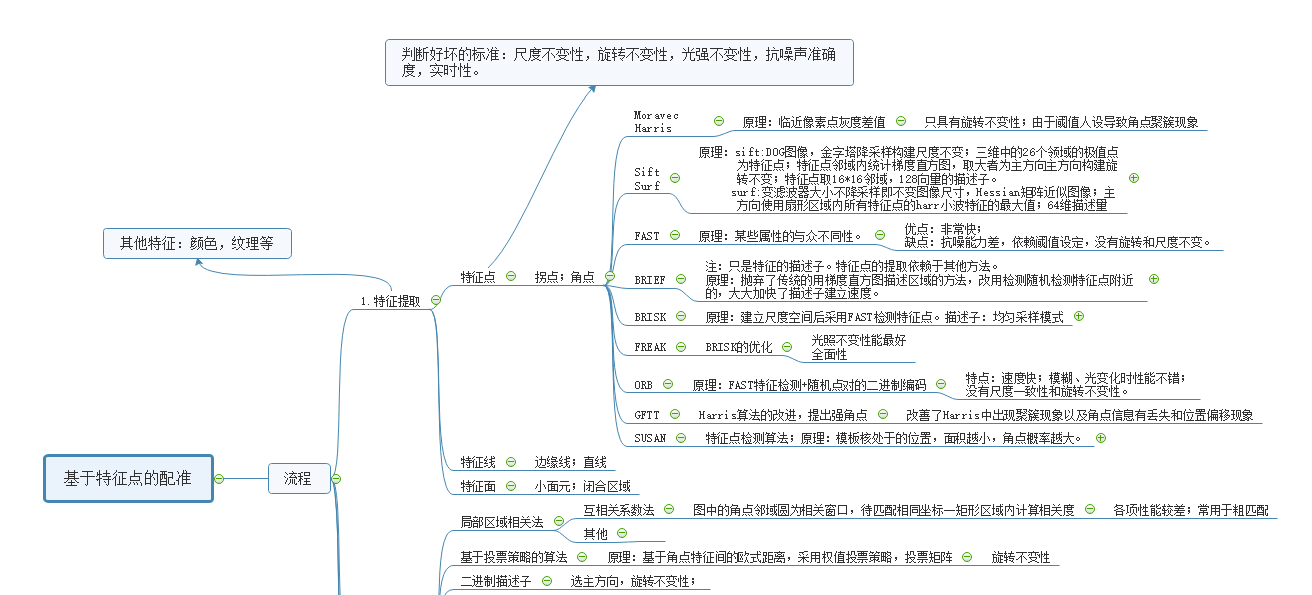
2.特征匹配：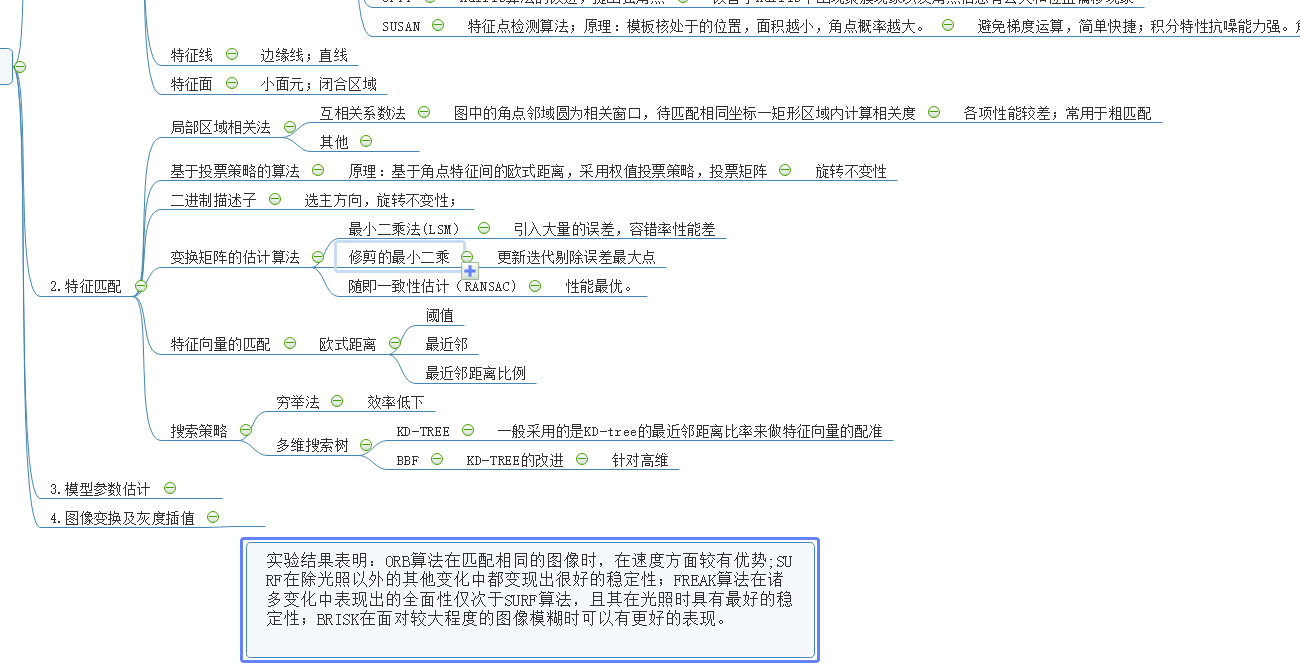

参考文献

2.5参考文献 [1] Barnea D I , Silverman H F . A Class of Algorithms for Fast Digital Image Registration[J]. IEEE Transactions on Computers, 1972, C-21(2):179-186.
[2] Moravec. Rover visual obstacle avoidance. In International Joint Conference on Artificial Intelligence, Vancouver, Canada, 1981. pp.785-790
[3] Harris C G, Stephens M J. A Combined Corner and Edge Detector[C] Proceedings of the 4th Alvey Vision Conference. Manchester, England: 1988.
[4] Smith S M, Brady J M. SUSAN—A New Approach to Low Level Image Processing[J]. International Journal of Computer Vision, 1997, 23(1):45-78.
[5] Lowe D G . Object Recognition from Local Scale-Invariant Features[C]// iccv. IEEE Computer Society, 1999.
[6] Bay H, Tuytelaars T, Gool L V. SURF: Speeded Up Robust Features[C]// European Conference on Computer Vision. 2006.
[7] Rosten E , Drummond T . Machine Learning for High-Speed Corner Detection[C]// European Conference on Computer Vision. Springer, Berlin, Heidelberg, 2006.
[8] Calonder M , Lepetit V , Fua P . BRIEF: Binary Robust Independent Elementary Features[J]. 2010.
[9] Rublee E , Rabaud V , Konolige K , et al. ORB: An efficient alternative to SIFT or SURF[C]// 2011 International Conference on Computer Vision. IEEE, 2012.
[10] Leutenegger S , Chli M , Siegwart R Y . BRISK: Binary Robust invariant scalable keypoints[C]// IEEE International Conference on Computer Vision, ICCV 2011, Barcelona, Spain, November 6-13, 2011. IEEE, 2011.
[11] Alahi A , Ortiz R , Vandergheynst P . FREAK: Fast retina keypoint[C]// Computer Vision and Pattern Recognition (CVPR), 2012 IEEE Conference on. IEEE, 2012.
[12] Xu Z, Liu Y, Du S, et al. DFOB: Detecting and describing features by octagon filter bank for fast image matching[J]. Signal Processing Image Communication, 2016, 41:61-71.
[13] Miao Z, Jiang X, Yap K H. Contrast Invariant Interest Point Detection by Zero-Norm LoG Filter[J]. IEEE Transactions on Image Processing A Publication of the IEEE Signal Processing Society, 2016, 25(1):331.
[14] Canny J F. Finding Edges and Lines in Images[M]. 1983.
[15] Canny J . A Computational Approach To Edge Detection[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 1986, PAMI-8(6):679-698.
[16] Davies E R . A modified Hough scheme for general circle location[J]. Pattern Recognition Letters, 1988, 7(1):37-43.
[17] Lipkin B S, Rosenfeld A. Picture Processing and Psychopictorics[J]. Transactions of the American Microscopical Society, 1970, 91(2).
[18] Prescott J , Clary M , Wiet G , et al. Automatic registration of large set of microscopic images using high-level features[C]// IEEE International Symposium on Biomedical Imaging: Nano to Macro. IEEE Xplore, 2006.

https://github.com/muyizaozao/-