1.需求说明

求出决策树的字典存储形式数据后，绘制出决策树的图形，则会更形象认识和了解其决策树。
比如，有决策树的字典结构如下所示：

  1. tree_dict = {'house?': {'hourse_no': {'working?': {'work_no': 'refuse', 'work_yes': 'agree'}}, 'hourse_yes': 'agree'}}

要绘制出对应的如下决策树：
【决策树】有了决策树的字典结构后 ，如何用python绘制决策树？ - 图1
本章代码就是完成此需求的。

2. 代码

  1. # -*- coding: utf-8 -*-
  2. """
  3. @author: 蔚蓝的天空Tom
  4. Aim:得到决策树的字典后，需要使用python来绘制对应的决策树figure
  5. 输入决策树的字典，样例如下所示：
  6. dtree = {'house?': {'hourse_no': {'working?': {'work_no': 'refuse', 'work_yes': 'agree'}}, 'hourse_yes': 'agree'}}
  7. """
  9. import matplotlib.pyplot as plt
  11. #定义判断结点形状,其中boxstyle表示文本框类型,fc指的是注释框颜色的深度
  12. decisionNode = dict(boxstyle="round4", color='r', fc='0.9')
  13. #定义叶结点形状
  14. leafNode = dict(boxstyle="circle", color='m')
  15. #定义父节点指向子节点或叶子的箭头形状
  16. arrow_args = dict(arrowstyle="<-", color='g')
  18. def plot_node(node_txt, center_point, parent_point, node_style):
  19.     '''
  20.     绘制父子节点，节点间的箭头，并填充箭头中间上的文本
  21.     :param node_txt:文本内容
  22.     :param center_point:文本中心点
  23.     :param parent_point:指向文本中心的点
  24.     '''
  25.     createPlot.ax1.annotate(node_txt, 
  26.                             xy=parent_point,
  27.                             xycoords='axes fraction',
  28.                             xytext=center_point,
  29.                             textcoords='axes fraction',
  30.                             va="center",
  31.                             ha="center",
  32.                             bbox=node_style,
  33.                             arrowprops=arrow_args)
  35. def get_leafs_num(tree_dict):
  36.     '''
  37.     获取叶节点的个数
  38.     :param tree_dict:树的数据字典
  39.     :return tree_dict的叶节点总个数
  40.     '''
  41.     #tree_dict的叶节点总数
  42.     leafs_num = 0
  44.     #字典的第一个键，也就是树的第一个节点
  45.     root = list(tree_dict.keys())[0]
  46.     #这个键所对应的值，即该节点的所有子树。
  47.     child_tree_dict =tree_dict[root]
  48.     for key in child_tree_dict.keys():
  49.         #检测子树是否字典型
  50.         if type(child_tree_dict[key]).__name__=='dict':
  51.             #子树是字典型，则当前树的叶节点数加上此子树的叶节点数
  52.             leafs_num += get_leafs_num(child_tree_dict[key])
  53.         else:
  54.             #子树不是字典型，则当前树的叶节点数加1
  55.             leafs_num += 1
  57.     #返回tree_dict的叶节点总数
  58.     return leafs_num
  60. def get_tree_max_depth(tree_dict):
  61.     '''
  62.     求树的最深层数
  63.     :param tree_dict:树的字典存储
  64.     :return tree_dict的最深层数
  65.     '''
  66.     #tree_dict的最深层数
  67.     max_depth = 0
  69.     #树的根节点
  70.     root = list(tree_dict.keys())[0]
  71.     #当前树的所有子树的字典
  72.     child_tree_dict = tree_dict[root]
  74.     for key in child_tree_dict.keys():
  75.         #树的当前分支的层数
  76.         this_path_depth = 0
  77.         #检测子树是否字典型
  78.         if type(child_tree_dict[key]).__name__ == 'dict':
  79.             #如果子树是字典型，则当前分支的层数需要加上子树的最深层数
  80.             this_path_depth = 1 + get_tree_max_depth(child_tree_dict[key])
  81.         else:
  82.             #如果子树不是字典型，则是叶节点，则当前分支的层数为1
  83.             this_path_depth = 1
  84.         if this_path_depth > max_depth:
  85.             max_depth = this_path_depth
  87.     #返回tree_dict的最深层数
  88.     return max_depth
  90. def plot_mid_text(center_point, parent_point, txt_str):
  91.     '''
  92.     计算父节点和子节点的中间位置，并在父子节点间填充文本信息
  93.     :param center_point:文本中心点
  94.     :param parent_point:指向文本中心点的点
  95.     '''
  97.     x_mid = (parent_point[0] - center_point[0])/2.0 + center_point[0]
  98.     y_mid = (parent_point[1] - center_point[1])/2.0 + center_point[1]
  99.     createPlot.ax1.text(x_mid, y_mid, txt_str)
  100.     return
  102. def plotTree(tree_dict, parent_point, node_txt):
  103.     '''
  104.     绘制树
  105.     :param tree_dict:树
  106.     :param parent_point:父节点位置
  107.     :param node_txt:节点内容
  108.     '''
  110.     leafs_num = get_leafs_num(tree_dict)
  111.     root = list(tree_dict.keys())[0]
  112.     #plotTree.totalW表示树的深度
  113.     center_point = (plotTree.xOff+(1.0+float(leafs_num))/2.0/plotTree.totalW,plotTree.yOff)
  114.     #填充node_txt内容
  115.     plot_mid_text(center_point, parent_point, node_txt)
  116.     #绘制箭头上的内容
  117.     plot_node(root, center_point, parent_point, decisionNode)
  118.     #子树
  119.     child_tree_dict = tree_dict[root]
  120.     plotTree.yOff=plotTree.yOff-1.0/plotTree.totalD
  121.     #因从上往下画，所以需要依次递减y的坐标值，plotTree.totalD表示存储树的深度
  122.     for key in child_tree_dict.keys():
  123.         if type(child_tree_dict[key]).__name__ == 'dict':
  124.             plotTree(child_tree_dict[key],center_point,str(key))
  125.         else:
  126.             plotTree.xOff=plotTree.xOff+1.0/plotTree.totalW
  127.             plot_node(child_tree_dict[key],(plotTree.xOff,plotTree.yOff),center_point,leafNode)
  128.             plot_mid_text((plotTree.xOff,plotTree.yOff),center_point,str(key))
  129.     #h绘制完所有子节点后，增加全局变量Y的偏移
  130.     plotTree.yOff=plotTree.yOff+1.0/plotTree.totalD
  132.     return
  134. def createPlot(tree_dict):
  135.     '''
  136.     绘制决策树图形
  137.     :param tree_dict
  138.     :return 无
  139.     '''
  140.     #设置绘图区域的背景色
  141.     fig=plt.figure(1,facecolor='white')
  142.     #清空绘图区域
  143.     fig.clf()
  144.     #定义横纵坐标轴,注意不要设置xticks和yticks的值!!!
  145.     axprops = dict(xticks=[], yticks=[])
  146.     createPlot.ax1=plt.subplot(111, frameon=False, **axprops)
  147.     #由全局变量createPlot.ax1定义一个绘图区，111表示一行一列的第一个，frameon表示边框,**axprops不显示刻度
  148.     plotTree.totalW=float(get_leafs_num(tree_dict))
  149.     plotTree.totalD=float(get_tree_max_depth(tree_dict))
  150.     plotTree.xOff=-0.5/plotTree.totalW;
  151.     plotTree.yOff=1.0;
  152.     plotTree(tree_dict, (0.5,1.0), '')
  153.     plt.show()
  155. if __name__=='__main__':
  156.     tree_dict = {'house?': {'hourse_no': {'working?': {'work_no': 'refuse', 'work_yes': 'agree'}}, 'hourse_yes': 'agree'}}
  157.     createPlot(tree_dict)

3.运行结果

3.1 如果树的字典存储为

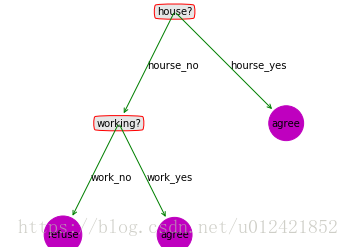
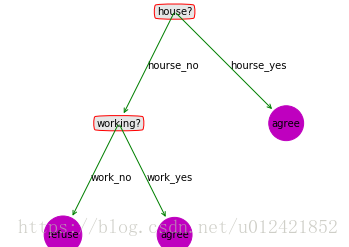
  1. tree_dict = {'house?': {'hourse_no': {'working?': {'work_no': 'refuse', 'work_yes': 'agree'}}, 'hourse_yes': 'agree'}}

则绘制的树图形为：

【决策树】有了决策树的字典结构后 ，如何用python绘制决策树？ - 图2
3.2 如果树的字典存储为

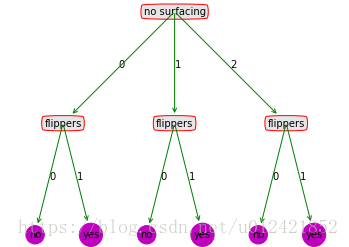
  1. tree_dict = {'no surfacing': {0:{'flippers': {0: 'no', 1: 'yes'}}, 1: {'flippers': {0: 'no', 1: 'yes'}}, 2:{'flippers': {0: 'no', 1: 'yes'}}}}

则绘制的树图形为：
【决策树】有了决策树的字典结构后 ，如何用python绘制决策树？ - 图3