ID3决策树是比较经典的决策树，在周志华的机器学习中，生成决策树的算法为：
image.png
算法的关键是如何选择最优划分属性，在ID3决策树中，用信息增益来指导决策树选择最优划分属性
首先定义信息熵为：
image.png
再定义信息增益为：
image.png
一般而言，信息增益越大，意味着使用属性a进行划分所获得的纯度提升越大，因此我们选择最大信息增益的属性作为最优划分属性。
Python实现思路

树的数据表示

既然要实现一棵树，首先要做的就是定义节点的数据结构，在C中，节点一般以结构体的形式存储，所以我们在Python中可以参考这一思路定义一个节点类：

  1. class Node():
  2.     """
  3.     ID3决策树的节点
  4.     parent -- 父节点
  5.     sons -- 子节点集合，即在该节点最优划分属性下每个属性值的分支
  6.     attrs -- 该节点下的最优划分属性
  7.     parent_attrs_value -- 表示该节点是父节点哪一个属性的分支
  8.     label -- 如果这个节点是叶子节点，则存放标签
  9.     """
  10.     def __init__(self, parent=None):
  11.         self.parent = parent            
  12.         self.sons = []                  
  13.         self.attr = None                
  14.         self.parent_attrs_value = None  
  15.         self.label = None

但在实际操作中，使用这一方法给代码的调试增加了难度，同时不利于后面用Graphviz包实现决策树的可视化，因此本文考虑使用另一种数据结构表示树，就是Python中的字典，我们先来看看对于西瓜书中给出的一颗决策树，用字典是如何表示的：
西瓜书中的一颗决策树：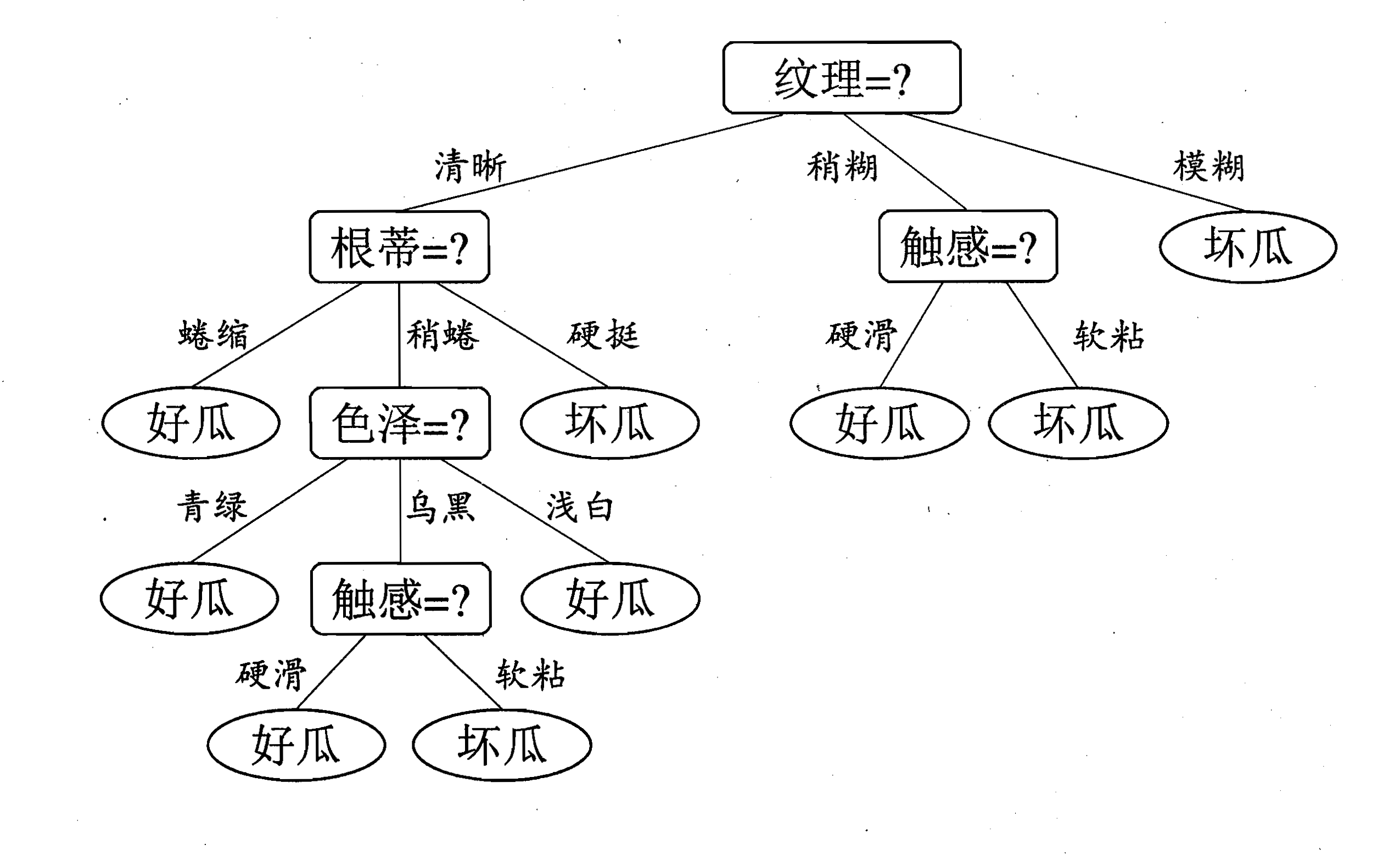
image.png
对应的Python字典表示：

  1. tree = {<!-- -->'纹理':
  2.             {<!-- -->'清晰':
  3.                 {<!-- -->'根蒂':
  4.                     {<!-- -->'蜷缩':
  5.                         {<!-- -->'label':'是'},
  6.                     '稍蜷':
  7.                         {<!-- -->'色泽':
  8.                             {<!-- -->'青绿':
  9.                                 {<!-- -->'label':'是'},
  10.                             '乌黑':
  11.                                 {<!-- -->'触感':
  12.                                     {<!-- -->'硬滑':
  13.                                         {<!-- -->'label':'是'},
  14.                                     '软粘':
  15.                                         {<!-- -->'label':'否'}}},
  16.                             '浅白':
  17.                                 {<!-- -->'label':'是'}}},
  18.                     '硬挺':
  19.                         {<!-- -->'label':'否'}}},
  20.             '稍糊':
  21.                 {<!-- -->'触感':
  22.                     {<!-- -->'硬滑':
  23.                         {<!-- -->'label':'否'},
  24.                     '软粘':
  25.                         {<!-- -->'label':'是'}}},
  26.             '模糊':
  27.                 {<!-- -->'label':'否'}}}

如何可视化决策树

在本文中，使用Graphviz包进行决策树的可视化，这里是官网和文档
只需使用几条简单的代码便可将决策树的节点绘制出来：

  1. g = graphviz.Digraph(name=,filename=, format='png')
  2. g.node(name=, label=, fontname="Microsoft YaHei", shape=)
  3. g.edge(tail_name, head_name, label=, fontname="Microsoft YaHei")
  4. g.view()

要注意，如果决策树的信息是中文的，要在fontname参数中指定中文字体，不然会出现乱码
Python代码
DecesionTree.py

  1. import numpy as np
  2. import scipy.io as sio
  3. from collections import Counter
  4. from graphviz import Digraph
  6. class DecisionTree():
  7.     """
  8.     一个构建ID3决策树的类
  9.     attrs -- 存放属性的字典, 字典中，键为属性名，值为属性的取值，最后一个属性为标签属性
  10.     X -- 训练数据
  11.     y -- 标签
  12.     attr_idx -- 属性列索引
  13.     tree -- 生成的决策树，用字典形式存放
  14.     node_name -- 用于对决策树的可视化，在graphviz中对节点的命名
  15.     """
  16.     def __init__(self):
  17.         self.attrs = None
  18.         self.X = None
  19.         self.y = None
  20.         self.attr_idx = None
  21.         self.tree = {<!-- -->}
  22.         self.node_name = "0"
  25.     def get_attrs(self, data):
  26.         """
  27.         对数据集进行处理，得到属性与对应的属性取值
  28.         args:
  29.         data -- 输入的数据矩阵, shape=(samples+1, features), dtype='<U?', 其中，第一行为属性，最后一列为标签
  30.         returns:
  31.         attrs -- 存放属性的字典, 字典中，键为属性名，值为属性的取值
  32.         """
  33.         attrs = {<!-- -->}
  34.         for i in range(data.shape[1]):
  35.             attrs_values = sorted(set(data[1:, i]))
  36.             attrs[data[0][i]] = attrs_values
  38.         self.attrs = attrs
  39.         return attrs
  42.     def generate_tree(self, data):
  43.         """
  44.         生成决策树
  45.         args:
  46.         data -- 输入的数据矩阵, shape=(samples+1, features+label), dtype='<U?', 其中，第一行为属性，最后一列为标签
  47.         """
  48.         self.X = data[1:, :-1]
  49.         self.y = data[1:, -1]
  51.         # 先创建一个不含label属性的纯变量属性字典
  52.         pure_attrs = self.attrs.copy()
  53.         del(pure_attrs['label'])
  54.         # 构造一个只含属性名的列表
  55.         attr_names = [attr_name for attr_name in pure_attrs.keys()]
  56.         # 将属性名编号，方便查找其在数据中对应的列
  57.         attr_idx = {<!-- -->}
  58.         for num, attr in enumerate(attr_names):
  59.             attr_idx[attr] = num
  60.         self.attr_idx = attr_idx
  62.         # 生成根节点
  63.         self.tree['root_node'] = {<!-- -->}
  64.         self._generate_tree(self.X, self.y, self.tree['root_node'], pure_attrs, attr_idx)
  65.         self.tree = self.tree['root_node']
  68.     def _generate_tree(self, X, y, node, attrs, attr_idx):
  69.         """
  70.         递归生成决策树
  71.         args:
  72.         X -- 输入的数据矩阵, shape=(samples, features), dtype='<U?'
  73.         y -- 标签, shape=(samples, )
  74.         parent_node -- 父节点，此次递归函数是父节点的某一个属性值的递归
  75.         attrs -- 属性字典, 即从父节点分支到现在的节点时，还没有被划分的属性
  76.         attr_idx -- 属性在数据中列索引
  77.         """
  79.         #--------- 如果训练集中样本全属于同一类别 ---------#
  80.         if len(set(y.tolist())) == 1:
  81.             node['label'] = y[0]
  82.             return
  84.         #-------- 如果属性集为空集或者训练集中样本在属性集上取值相同 ---------#
  85.         # 判断训练集样本在属性集中取值是否相同
  86.         same = True
  87.         for i in range(X.shape[1]):
  88.             if len(set(X[:, i].tolist())) > 1:
  89.                 same = False
  91.         if not attrs or same:
  92.             y_counter = Counter(y)
  93.             most_y = y_counter.most_common()[0][0]
  94.             node['label'] = most_y
  95.             return
  97.         #--------- 选择最优属性生成分支 ---------#
  98.         # 选出最优划分属性
  99.         optimal_attr = self.choose_optimal_attr(X, y, attrs, attr_idx)
  100.         node[optimal_attr] = {<!-- -->}
  101.         node = node[optimal_attr]
  102.         # 对于最优划分属性下每个属性值
  103.         for attr_value in attrs[optimal_attr]:
  104.             # 生成分支
  105.             node[attr_value] = {<!-- -->}
  106.             # 令Dv表示X中在optimal_attr上取值为attr_value的样本子集
  107.             Dv = X.copy()
  108.             attr_value_idx = Dv[:, attr_idx[optimal_attr]] == attr_value
  109.             Dv = Dv[attr_value_idx, :]
  110.             y_Dv = y[attr_value_idx]
  111.             Dv = np.delete(Dv, attr_idx[optimal_attr], 1)
  112.             # 如果Dv为空
  113.             if Dv.size == 0:
  114.                 # 将分支节点标记为叶节点，其类别标记为X中样本最多的类，即统计y
  115.                 y_counter = Counter(y)
  116.                 most_y = y_counter.most_common()[0][0]
  117.                 node[attr_value]['label'] = most_y
  118.             else:
  119.                 # 更新属性字典
  120.                 new_attrs = attrs.copy()
  121.                 del(new_attrs[optimal_attr])
  122.                 # 更新属性列索引
  123.                 new_attr_names = [new_attr_name for new_attr_name in new_attrs.keys()]
  124.                 new_attr_idx = {<!-- -->}
  125.                 for num, attr in enumerate(new_attr_names):
  126.                     new_attr_idx[attr] = num
  127.                 self._generate_tree(Dv, y_Dv, node[attr_value], new_attrs, new_attr_idx)
  130.     def compute_Ent(self, y):
  131.         """
  132.         计算给出属性名列表所对应的所有样本的信息熵
  133.         args:
  134.         y -- 标签数组, shape=(samples, )
  135.         return:
  136.         Ent -- 样本的信息熵
  137.         """
  138.         Ent = 0
  139.         m = np.size(y)
  140.         for label in self.attrs['label']:
  141.             pk = np.sum(y == label)
  142.             pk = pk / m
  143.             log2pk = np.log2(pk + 1e-8) # 防止算得0,导致返回nan
  144.             Ent -= pk * log2pk
  145.         return Ent
  148.     def choose_optimal_attr(self, X, y, attrs, attr_idx):
  149.         """
  150.         选择最优划分属性 划分标准：属性的信息增益
  151.         args:
  152.         X -- 输入的数据矩阵, shape=(samples, features), dtype='<U?'
  153.         y -- 标签, shape=(samples, )
  154.         attrs -- 属性字典
  155.         attr_idx -- 属性在数据中列索引
  156.         returns:
  157.         max_gain_attr -- 最大的信息增益对应的属性
  158.         """
  159.         # 计算当前所含属性对应所有样本的信息熵
  160.         Ent = self.compute_Ent(y)
  161.         m = np.size(y)
  162.         # 记录当前最大的信息增益以及对应的属性
  163.         max_gain = 0
  164.         max_gain_attr = None
  166.         # 计算每一个属性的信息增益
  167.         for attr, idx in attr_idx.items():
  168.             x = X[:, idx]
  169.             gain = Ent
  170.             # 计算一个属性中每个属性值的信息熵
  171.             for attr_value in attrs[attr]:
  172.                 _y = y[x==attr_value]
  173.                 if _y.size != 0:
  174.                     ent = self.compute_Ent(_y)
  175.                 else:
  176.                     ent = 0
  177.                 gain -= np.size(_y) / m * ent
  178.             if gain > max_gain:
  179.                 max_gain = gain
  180.                 max_gain_attr = attr
  182.         return max_gain_attr
  185.     def predict(self, predict_x):
  186.         """
  187.         预测样本结果
  188.         args:
  189.         predict_x -- 预测样本数据矩阵 shape=(samples, features)
  190.         returns:
  191.         predict_y -- 样本的预测结果 shape=(samples, )
  192.         """
  193.         s = predict_x.shape[0]
  194.         predict_y = []
  195.         for i in range(s):
  196.             node = self.tree
  197.             while(1):
  198.                 if 'label' in node.keys():
  199.                     predict_y.append(node['label'])
  200.                     break
  201.                 elif list(node.keys())[0] in self.attrs.keys():
  202.                     attr = list(node.keys())[0]
  203.                     idx = self.attr_idx[attr]
  204.                     node = node[attr]
  205.                 else:
  206.                     node = node[predict_x[i, idx]]
  207.         return predict_y
  210.     def tree_traversal(self, g, parent_node, parent_node_name, parent_attr, parent_attr_value):
  211.         """
  212.         对树进行遍历，生成可视化的节点
  213.         g -- 要绘制的有向图
  214.         parent_node -- 父节点
  215.         parent_node_name -- 父节点在有向图中的代号
  216.         parent_attr -- 父节点的属性
  217.         parent_attr_value -- 父节点到该节点的属性值
  218.         """
  219.         if (parent_attr and parent_attr_value) is None:
  220.             if 'label' in parent_node.keys():
  221.                 g.node(name=self.node_name, label=parent_node['label'], fontname="Microsoft YaHei")
  222.                 return
  223.             else:
  224.                 attr = list(parent_node.keys())[0]
  225.                 node = parent_node[attr]
  226.                 parent_node_name = "0"
  227.                 for attr_value in node.keys():
  228.                     self.tree_traversal(g, node[attr_value], parent_node_name, attr, attr_value)
  229.         else:
  230.             if 'label' in parent_node.keys():
  231.                 g.node(name=parent_node_name, label=parent_attr, fontname="Microsoft YaHei", shape='box')
  232.                 self.node_name = str(int(self.node_name) + 1)
  233.                 g.node(name=self.node_name, label=parent_node['label'], fontname="Microsoft YaHei")
  234.                 g.edge(parent_node_name, self.node_name, label=parent_attr_value, fontname="Microsoft YaHei")
  235.             else:
  236.                 attr = list(parent_node.keys())[0]
  237.                 g.node(name=parent_node_name, label=parent_attr, fontname="Microsoft YaHei", shape='box')
  238.                 self.node_name = str(int(self.node_name) + 1)
  239.                 g.node(name=self.node_name, label=attr, fontname="Microsoft YaHei", shape='box')
  240.                 g.edge(parent_node_name, self.node_name, label=parent_attr_value, fontname="Microsoft YaHei")
  241.                 node = parent_node[attr]
  242.                 parent_node_name = self.node_name
  243.                 for attr_value in node.keys():
  244.                     self.tree_traversal(g, node[attr_value], parent_node_name, attr, attr_value)
  247.     def tree_visualize(self, file_name=None):
  248.         """
  249.         将决策树可视化
  250.         args:
  251.         file_name -- 若给出该参数，则将决策树保存为file_name的图片
  252.         """
  253.         if file_name:
  254.             g = Digraph("Decision Tree", filename=file_name, format='png')
  255.         else:
  256.             g = Digraph("Decision Tree")
  257.         self.tree_traversal(g, self.tree, None, None, None)
  258.         g.view()
  261. if __name__ == "__main__":
  262.     pass

主函数，以西瓜树的西瓜数据集为例生成决策树，原数据集是Matlab的cell数组，并以mat文件存放，因此需要预处理一下：

  1. import numpy as np
  2. import scipy.io as sio
  3. from DecisionTree import DecisionTree
  5. def preprocess():
  6.     raw_data = sio.loadmat('watermelon.mat')
  7.     raw_data = raw_data['watermelon']
  8.     data = np.zeros(raw_data.shape, dtype='<U20')
  10.     for i in range(data.shape[0]):
  11.         for j in range(data.shape[1]):
  12.             data[i, j] = raw_data[i, j][0]
  14.     data[0, -1] = 'label'
  15.     return data
  17. def main_1():
  18.     """
  19.     完整决策树
  20.     """
  21.     data = preprocess()
  22.     DTree = DecisionTree()
  23.     attrs = DTree.get_attrs(data)
  24.     DTree.generate_tree(data)
  25.     DTree.tree_visualize('watermelob_tree')
  27. def main_2():
  28.     """
  29.     留出两个样本作为测试集
  30.     """
  31.     data = preprocess()
  32.     train_idx = np.delete(np.arange(0, 18), [8, 17])
  33.     test_idx = [8, 17]
  34.     train_data = data[train_idx, :]
  35.     test_data = data[test_idx, :]
  36.     test_X = test_data[:, :-1]
  37.     test_y = test_data[:, -1]
  39.     DTree = DecisionTree()
  40.     DTree.get_attrs(train_data)
  41.     DTree.generate_tree(train_data)
  42.     predict_y = DTree.predict(test_X)
  43.     print(predict_y)
  44.     DTree.tree_visualize('watermelon_tree_2')
  46. main_1()

最终生成的决策树图片为：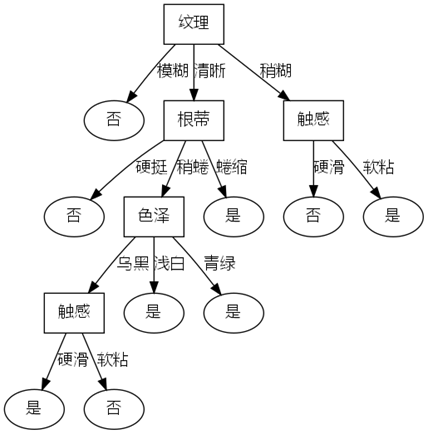
image.png
到这里我们就成功地用Python实现了ID3决策树！

https://www.codenong.com/cs109634151/