叉乘:Cross
运算方式:向量 x 向量
运算结果:向量
————————————————————————————-
几何意义:两个向量的叉乘,垂直于两向量
运算顺序:运算顺序不同,结果不一样
技巧:(以正旋转方向为准,用该手坐标系的那只手)
拇指为 法线N
食指为 向量A
中指为 向量B
(握手时先扫过的为A,后扫过的为B)
A x B = N
B x A = -N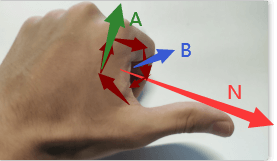
叉乘推导
已知一个平面内,两条相交不平行的向量A、B 求垂直于该平面的法向量 N
| 因为垂直于平面的法线有无数条,所以我们设N的z分量为1,其他的为未知数。 已知:A=(Ax,Ay,Az) B=(Bx,By,Bz) 设: N=(X,Y,1) |
|
|---|---|
| 因为向量A、B在平面内,且法向量N垂直于平面 所以A⊥N 、B⊥N |
|
| 根据点乘原理可列出 A·N=0 B·N=0 带入分量可得二元方程组: XAx+YAy+Az =0 XBx+YBy+Bz =0 |
|
| 利用高斯消元法: X = (ByAz-AyBz) / (AyBx-ByAx) Y = (BxAz-AxBz) / (AxBy-BxAy) |
|
| 法向量即为 N=( (ByAz-AyBz)/(AyBx-ByAx) , (BxAz-AxBz) / (AxBy-BxAy) , 1) 化简分母 N=( A**yBz-ByAz , BxAz-AxB**z , A**xBy-BxAy** ) |
速记叉乘
| 第一步 | 写两遍A、B向量的分量,并去头去尾 A__x Ay Az Ax Ay A__z B__x By Bz Bx By B__z |
|
|---|---|---|
| 第二步 | 剩下的交叉相乘即为向量N的分量 Ay Az Ax A__y By Bz Bx B__y |
X = AyBz - ByAz
—————————————-
Ay Az Ax A__y
By Bz Bx B__y
Y = AzBx - AyBx
——————————————
Ay Az Ax A__y
By Bz Bx B__y
Z = AxBy - BxAy | |
| 第三步 | N= (X,Y,Z)
=(A**yBz - ByAz, AzBx - AyB**x, A**xBy - BxAy**) | |

