冒泡排序
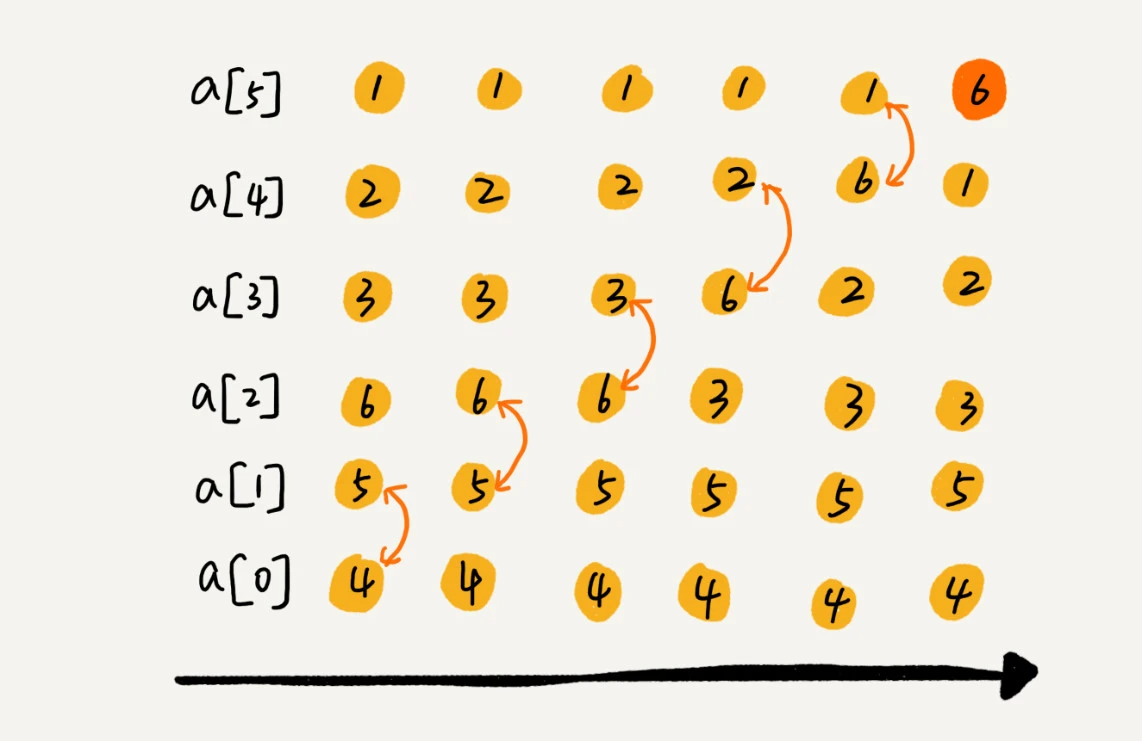
比较相邻元素并比较大小,交换两者位置,每遍历一次数组,都有一个最值被挑出来,放到数组末尾
// 冒泡排序,a表示数组,n表示数组大小public void bubbleSort(int[] a, int n) {if (n <= 1) return;for (int i = 0; i < n; ++i) {// 提前退出冒泡循环的标志位boolean flag = false;for (int j = 0; j < n - i - 1; ++j) {if (a[j] > a[j+1]) { // 交换int tmp = a[j];a[j] = a[j+1];a[j+1] = tmp;flag = true; // 表示有数据交换}}if (!flag) break; // 没有数据交换,提前退出}}
插入排序
实现思路
将要进行排序的数组分为已排序区间和未排序区间。初始已排序区间只有一个元素,就是数组的第一个元素。插入算法的核心思想是取未排序区间中的元素,在已排序区间中找到合适的插入位置将其插入,并保证已排序区间数据一直有序。重复这个过程,直到未排序区间中元素为空,算法结束。
// 插入排序,a表示数组,n表示数组大小public void insertionSort(int[] a, int n) {if (n <= 1) return;for (int i = 1; i < n; ++i) {int value = a[i];int j = i - 1;// 查找插入的位置for (; j >= 0; --j) {if (a[j] > value) {a[j+1] = a[j]; // 数据移动} else {break;}}a[j+1] = value; // 插入数据}}
选择排序
实现思路
选择排序算法的实现思路有点类似插入排序,也分已排序区间和未排序区间。但是选择排序每次会从未排序区间中找到最小的元素,将其放到已排序区间的末尾。(交换位置)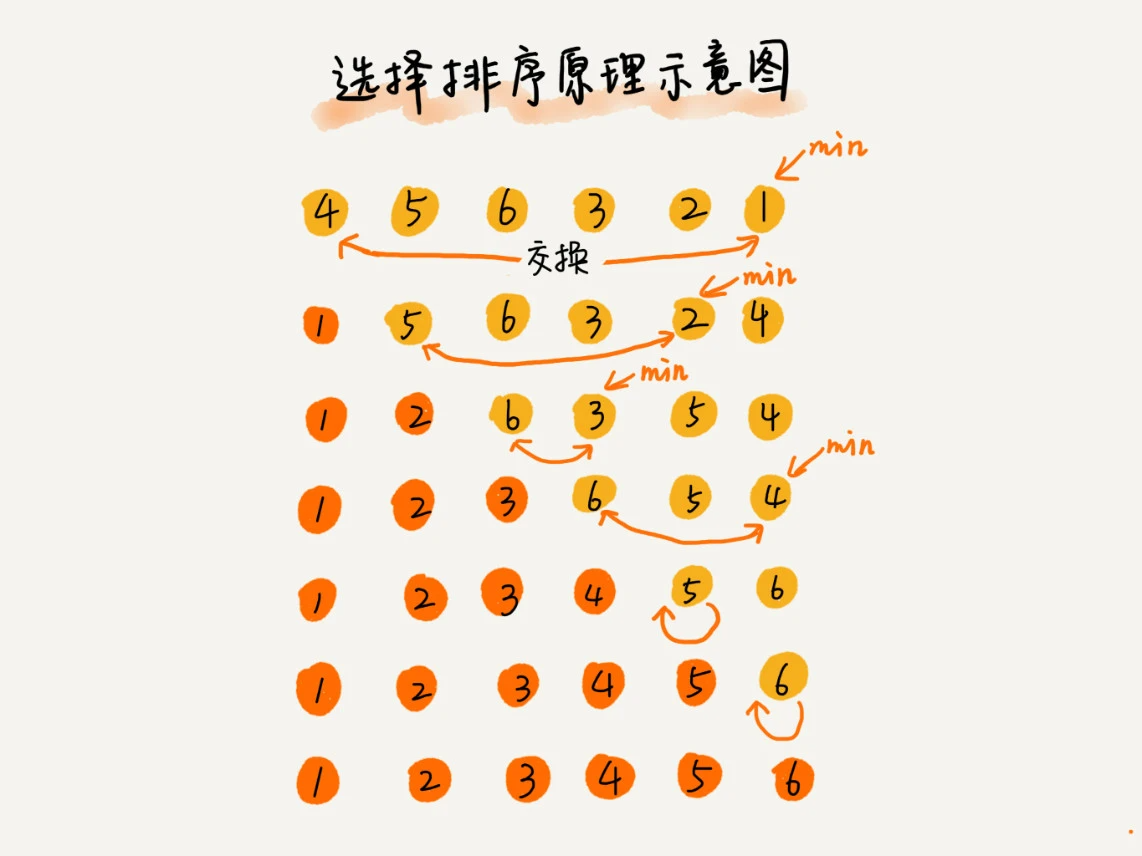
比较
| 排序方法 | 空间复杂度 | 时间复杂度(最好,最坏,平均) | 是否稳定(同值保持原来顺序) | 元素移动个数 |
|---|---|---|---|---|
| 冒泡 | O(1) | O(n) , O(n2) , O(n2) | 是 | 逆序数 |
| 插入 | O(1) | O(n) , O(n2) , O(n2) | 是 | 逆序数 |
| 选择 | O(1) | O(n2) , O(n2) , O(n2) | 否 | \ |
冒泡和插入
冒泡排序中数据的交换操作:
if (a[j] > a[j+1]) { // 交换
int tmp = a[j];
a[j] = a[j+1];
a[j+1] = tmp;
flag = true;
}
插入排序中数据的移动操作:
if (a[j] > value) {
a[j+1] = a[j]; // 数据移动
} else {
break;
}
已知两种排序方式需要移动的元素个数都是数组的逆序数,但从代码实现上来看,冒泡排序的数据交换要比插入排序的数据移动要复杂,冒泡排序需要 3 个赋值操作,而插入排序只需要 1 个。
我们把执行一个赋值语句的时间粗略地计为单位时间(unit_time),然后分别用冒泡排序和插入排序对同一个逆序度是 K 的数组进行排序。用冒泡排序,需要 K 次交换操作,每次需要 3 个赋值语句,所以交换操作总耗时就是 3*K 单位时间。而插入排序中数据移动操作只需要 K 个单位时间。

