浮点数的不确定性

F12 进入到浏览器开发者模式的 Console
>>> 0.3 + 0.6
0.8999999999999999

实数为无限集，而计算机中通常用 32 或 64 比特表示一个数据，以 32 比特为例，可以表示的数据的个数为浮点数 - 图1 约为 40 亿个，由鸽巢原理可知必有不同的实数有相同的二进制表示方式。

定点数表示

BCD 编码格式：用 4 个比特来表示 0～9 的整数，那么 32 个比特就可以表示 8 个这样的整数。然后我们把最右边的 2 个 0～9 的整数，当成小数部分；把左边 6 个 0～9 的整数，当成整数部分。这样，我们就可以用 32 个比特，来表示从 0 到 999999.99 这样 1 亿个实数了。

该方法直观清楚且一定范围内保证准确，通常用于超市收银机，但该方式有几个明显缺点：首先浪费内存空间，其次是在其他程序中，这样的表示方式不能表示很大或者很小的数据。

浮点数表示

为了保障数据尽量准确的同时，提高数据可以表示的范围，这里使用科学计数法，以单精度浮点数举例：
第一部分是一个符号位，用来表示是正数还是负数。我们一般用 s 来表示。浮点数不像正数分符号数还是无符号数，所有的浮点数都是有符号的。

至于指数E，情况就比较复杂，在扩展部分讲解。

最后，是一个 23 个比特组成的有效数位。我们用 f 来表示。综合科学计数法，我们的浮点数就可以表示成下面这样：

浮点数 - 图3

从表达式可以看出，该方式不能表示 0，这里就要用到之前保留的 0 和 255 来表示一些特殊的数据：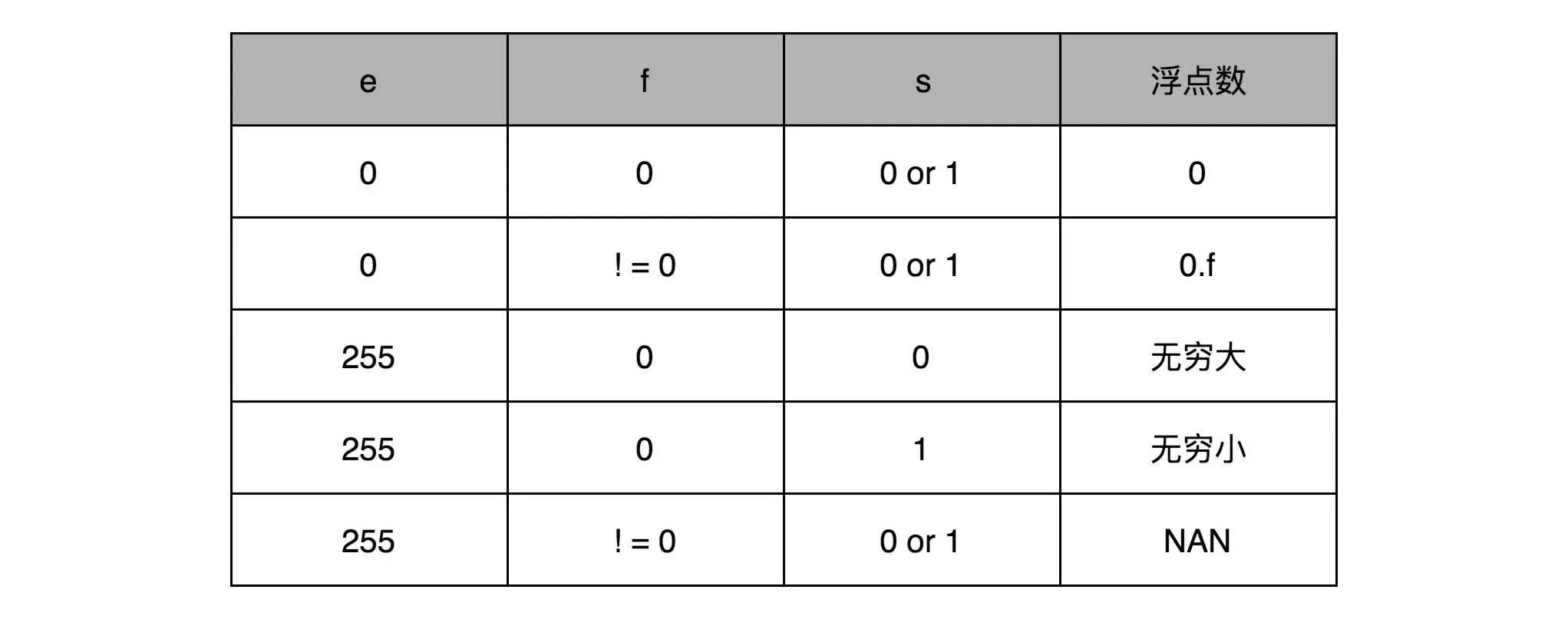

注意对表格进行修改：第三行第四列：浮点数 - 图5

这里的 bias 指的就是 e 的二进制代表的值

在这样的浮点数表示下，不考虑符号的话，浮点数能够表示的最小的数和最大的数，差不多是 1.17×10−38 和 3.40×1038。比前面的 BCD 编码能够表示的范围大多了。

回到最开始的计算，正是因为浮点数不能精确表示 0.3 和 0.6，所以最后无法正确得到需要的结果。

浮点数的二进制转化

这里使用分数 9.1 举例：

首先，将这个十进制的数据转换为二进制，整数部分不在阐述，小数部分：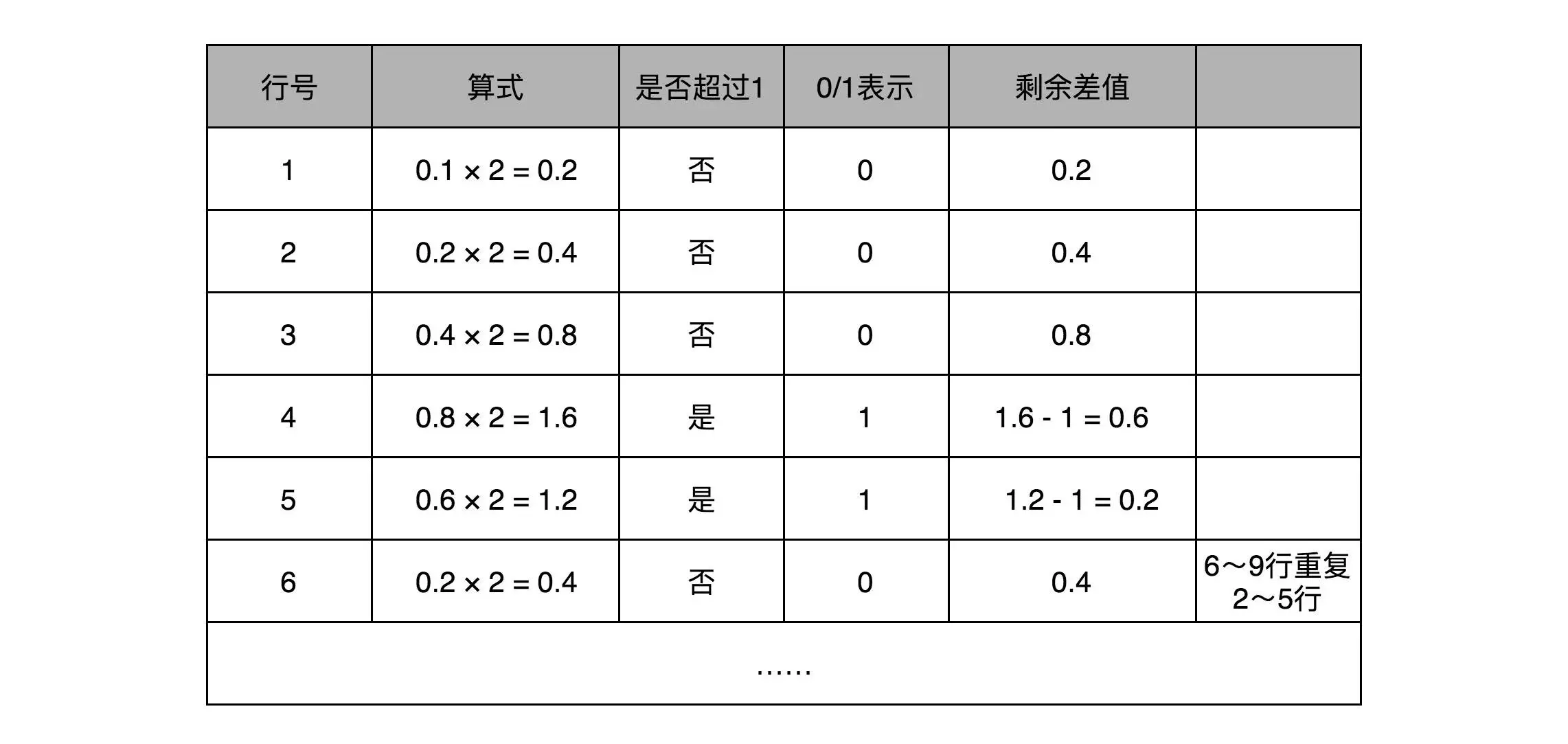

然后，我们把整数部分和小数部分拼接在一起，9.1 这个十进制数就变成了 1001.000110011… 这样一个二进制表示，进行移位可得：1.001000110011…×23。

结合上部分可得：符号位 s = 0，对应的有效位 f=001000110011… 。因为 f 最长只有 23 位，那这里“0011”无限循环，最多到 23 位就截止了。于是，f=00100011001100110011 001。最后的一个“0011”循环中的最后一个“1”会被截断掉。指数为 3，所以 e 的二进制表示数值应为 127 + 3 = 130 即 10000010 。
于是 9.1 的二进制表示为：0 10000010 0010 0011001100110011 001

将得到的这个数据按照规则在转化为十进制得到：9.09999942779541015625

浮点数加法和精度损失

主要规则：先对齐，再计算。

两个浮点数的指数位可能是不一样的，所以我们要把两个的指数位，变成一样的，然后只去计算有效位的加法就好了。

那我们在计算 0.5+0.125 的浮点数运算的时候，首先要把两个的指数位对齐，也就是把指数位都统一成两个其中较大的 -1。对应的有效位 1.00…也要对应右移两位，因为 f 前面有一个默认的 1，所以就会变成 0.01。然后我们计算两者相加的有效位 1.f，就变成了有效位 1.01，而指数位是 -1，这样就得到了我们想要的加法后的结果。

其中指数位较小的数，需要在有效位进行右移，在右移的过程中，最右侧的有效位就被丢弃掉了。这会导致对应的指数位较小的数，在加法发生之前，就丢失精度。两个相加数的指数位差的越大，位移的位数越大，可能丢失的精度也就越大。

Kahan Summation 算法

见链接

扩展延伸

指数位 E

首先，E 为一个无符号整数（unsigned int）。这意味着，如果 E 为 8 位，它的取值范围为 0~255；如果 E 为 11 位，它的取值范围为 0~2047 。但是，我们知道，科学计数法中的 E 是可以出现负数的，所以 IEEE 754 规定，E 的真实值必须再减去一个中间数，对于 8 位的 E ，这个中间数是 127；对于 11 位的 E，这个中间数是 1023。

比如，2^10 的 E 是10，所以保存成 32 位浮点数时，必须保存成 10+127=137，即 10001001。

然后，指数 E 还可以再分成三种情况：

（1）E 不全为 0 或不全为 1。这时，浮点数就采用上面的规则表示，即指数E的计算值减去 127（或1023），得到真实值，再将有效数字 M 前加上第一位的1。

（2）E 全为 0。这时，浮点数的指数 E 等于 1-127（或者1-1023），有效数字 M 不再加上第一位的 1，而是还原为 0.xxxxxx 的小数。这样做是为了表示 ±0，以及接近于 0 的很小的数字。

（3）E 全为 1。这时，如果有效数字 M 全为 0，表示 ±无穷大（正负取决于符号位 s）；如果有效数字 M 不全为 0，表示这个数不是一个数（NaN）。

直观展示浮点数计算

https://www.h-schmidt.net/FloatConverter/IEEE754.html

小结

浮点数的选择要注意环境，在进行金额交易时，要特别避免大数吃小数的情况的发生，但是在进行一些物理计算时，不需要数据太精确。

对于 64 位浮点数：符号位是1位，指数部分为11位，尾数部分为52位；当做加法的两个64位的浮点数的指数位相差52位后，较小的那个数就会因为要右移53位导致有效位数完全丢失；