第一章 多元统计分析概述
多元统计分析的定义
指针对多元数据的统计分析方法。多元的元指的是变量和信息维度。多元统计分析是同时考量多个变量,从多元数据集中获取信息的统计方法。
多元分析的方法简介
数据描述
统计推断
经典降维
用少数几个变量替代原有的数目庞大的变量,把重复的信息合并起来,既可以降低现有变量的维度,又不会丢失掉重要信息的思想,称为降维。
经典的降维方法包括主成分分析和因子分析。
主成分分析(PCA)用于构造“综合指标”,以将原始数据最大程度地区分开。
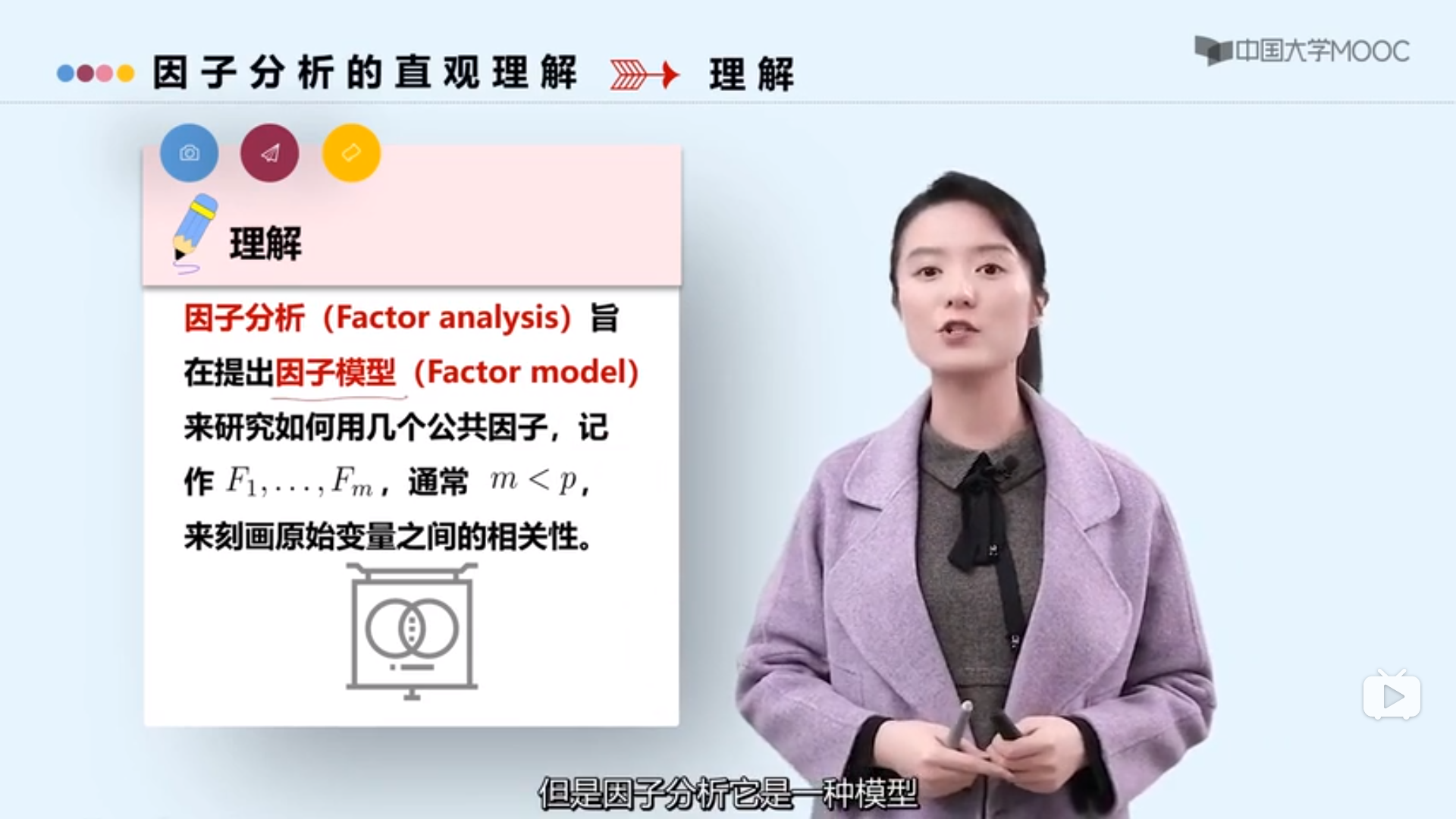
因子分析旨在用一个变量(公因子)代替原始高度相关的某几个变量。
目标归类
分类问题:用历史数据寻找分类规则,则判别分析(Discrimination),将新个体按照分类规则归至某一类(Classification)
聚类问题:定义刻画多元数据相似性/差异性的距离(Distance),将相似的聚在一起作为一类(Cluster)
多元分析的应用领域
生物信息分析
基因的聚类、疾病基因的定位、基因之间的关系、基因突变
第二章 多元数据的描述和展示
一元随机变量回顾
一元随机变量
随机总体:均值、方差与标准差
随机样本:样本均值、样本方差、样本标准差
二元随机变量
二元随机样本
协方差与独立性
可视化
随机向量
多元数据的特征和可视化
多元数据的矩阵展示
现有n个样本点,每个样本点包含p个变量的观测,则数据集可以表示为n×p矩阵。
均值向量(mean vector)
协方差的矩阵(convariance matrix)
协方差矩阵的用途
点击查看【bilibili】
刻画数据整体的离散性
定义统计距离
欧式距离:
标准化、统计距离:
马氏距离:
一、定义数据的离散程度
二、定义多元数据的马氏距离
随即向量的变换
随机向量的分割
均值向量的分割
变量的线性组合
第三章 多元正态分布
什么是多元正态分布
一元正态分布的回顾
一元正态分布的性质
- 整个分布可以仅用均值和方差来刻画
- 如果变量之间不相关,则它们相互独立
- 经典统计检验通常基于正态分布假设
- 正态分布可以模拟大量的自然现象
- 即使数据不服从正态分布,样本均值在大样本下也可以由其近似(中心极限定理)
密度函数
多元正态分布的性质
- P个变量的线性组合
相对地,如果y中元素所有的线性组合都服从一元正态分布,则y一定是多元正态分布。
极大似然估计
分布
评估多元正态性
评估一元正态性
评估多元数据正态性
检验向量的每一维是否都是一元正态分布
检验是否成对散点图存在非线性趋势
第四章 均值向量的检验
多元检验的动机
单样本均值向量检验
单样本协方差已知


单样本协方差未知
两样本均值向量检验(独立样本)
两样本均值向量检验(成对样本)
第五章 判别分析和分类分析
Discrimination Analysis and Classification Analysis
判别分析和分类分析
判别分析旨在寻找一种判别规则,利用变量的函数(判别函数)来描述、解释两组或多组群体间的区别。判别分析的最终目的通常是分类。
分类分析则给出分类结果:预测一个新观测对象的类别———-利用判别函数在新观测上的取值,找到该观察最有可能属于的类别。
判别分析和分类分析中,所有个体都有既定标签,即有“标准答案”可供监督,故其属于有监督学习(Supervised learning)
应用领域:
判别分析:分类规则(两群体Fisher线性判别分析)
判别分析:分类规则(多群体Fisher线性判别分析)
分类分析:分类结果(两群体Fisher分类)
两群体Fisher分类
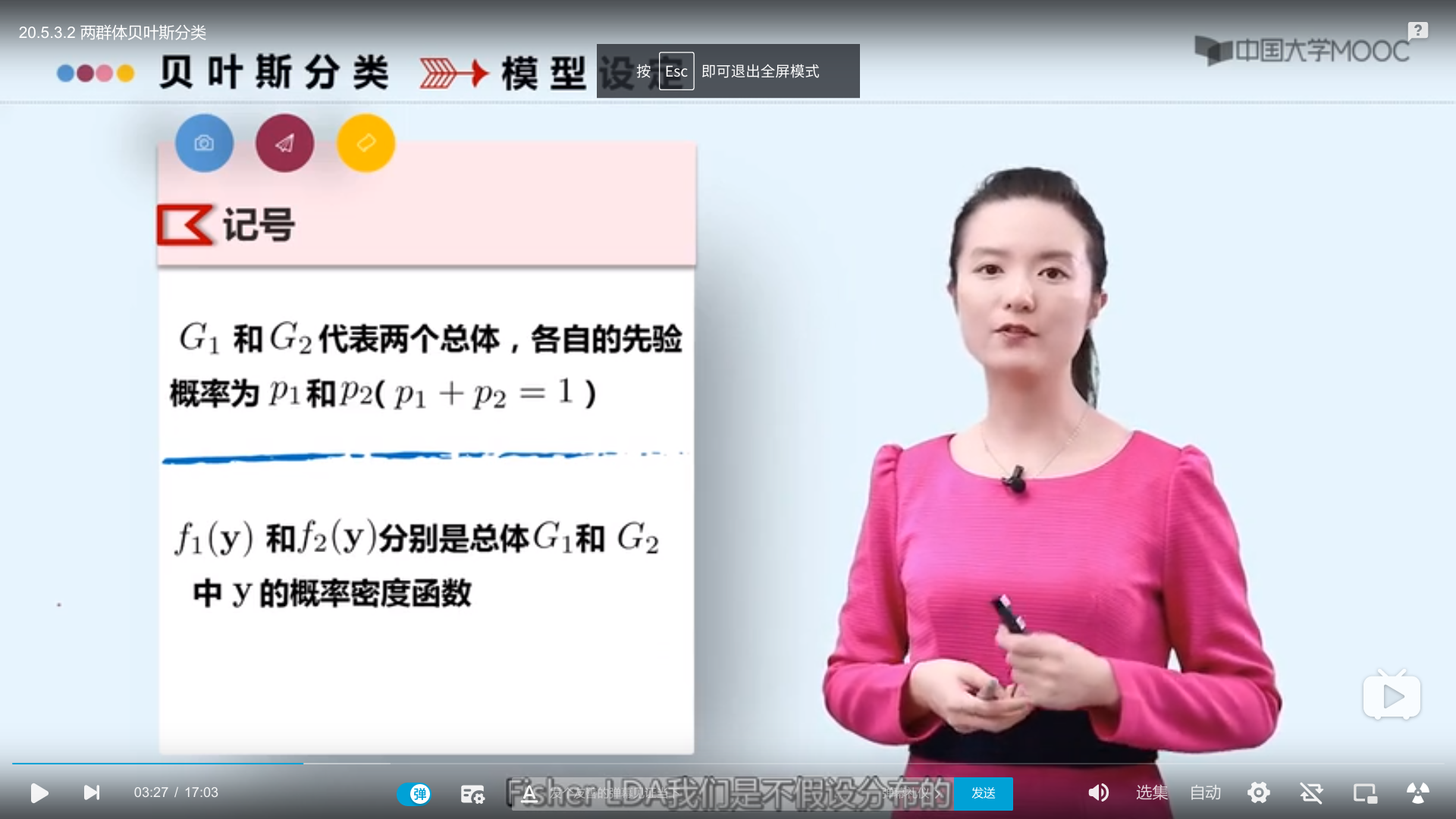
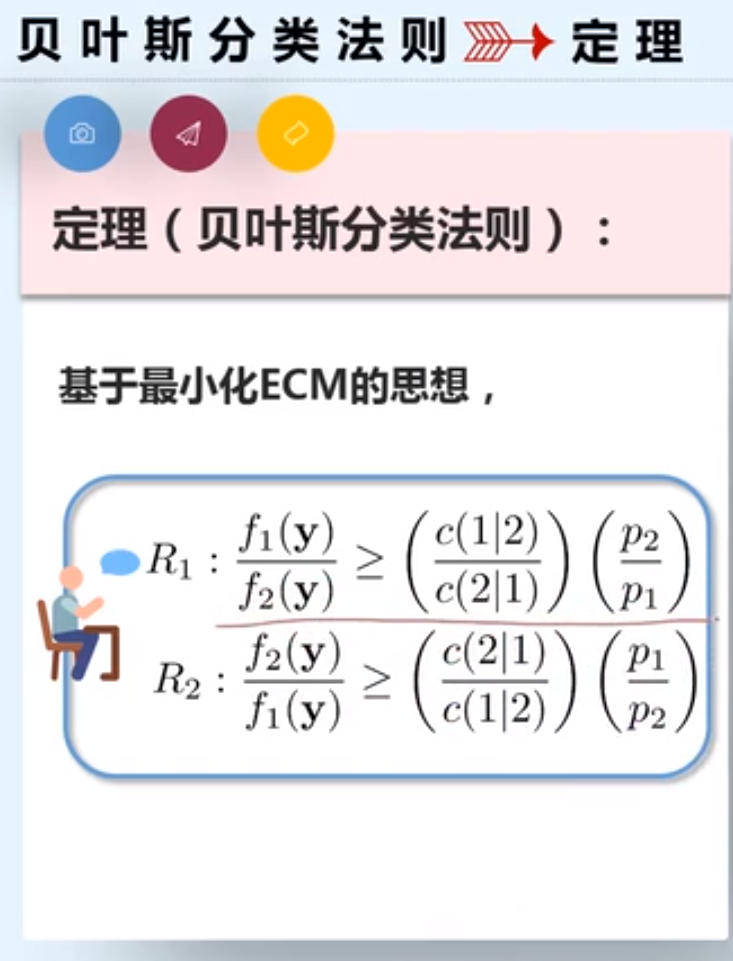
两群体贝叶斯分类
多群体分类
第六章 主成分分析
主成分分析思想
点击查看【bilibili】
主成分分析从所有可能的Y1,。。。。,Y6的线性组合模式中,寻找一个或几个(通常小于6个)可以最大程度区分学生的线性组合/加权平均。
线性判别分析(LDA)寻求最大化两个或多个群体之间的距离线性组合。
主成分分析(PCA)中只有一个群体,目标是找到能使这个群体中个体间分得最开的变量组合。
总体主成分分析
总体主成分推导
基于标准化的总体主成分分析
样本主成分分析
样本主成分推导
点击查看【bilibili】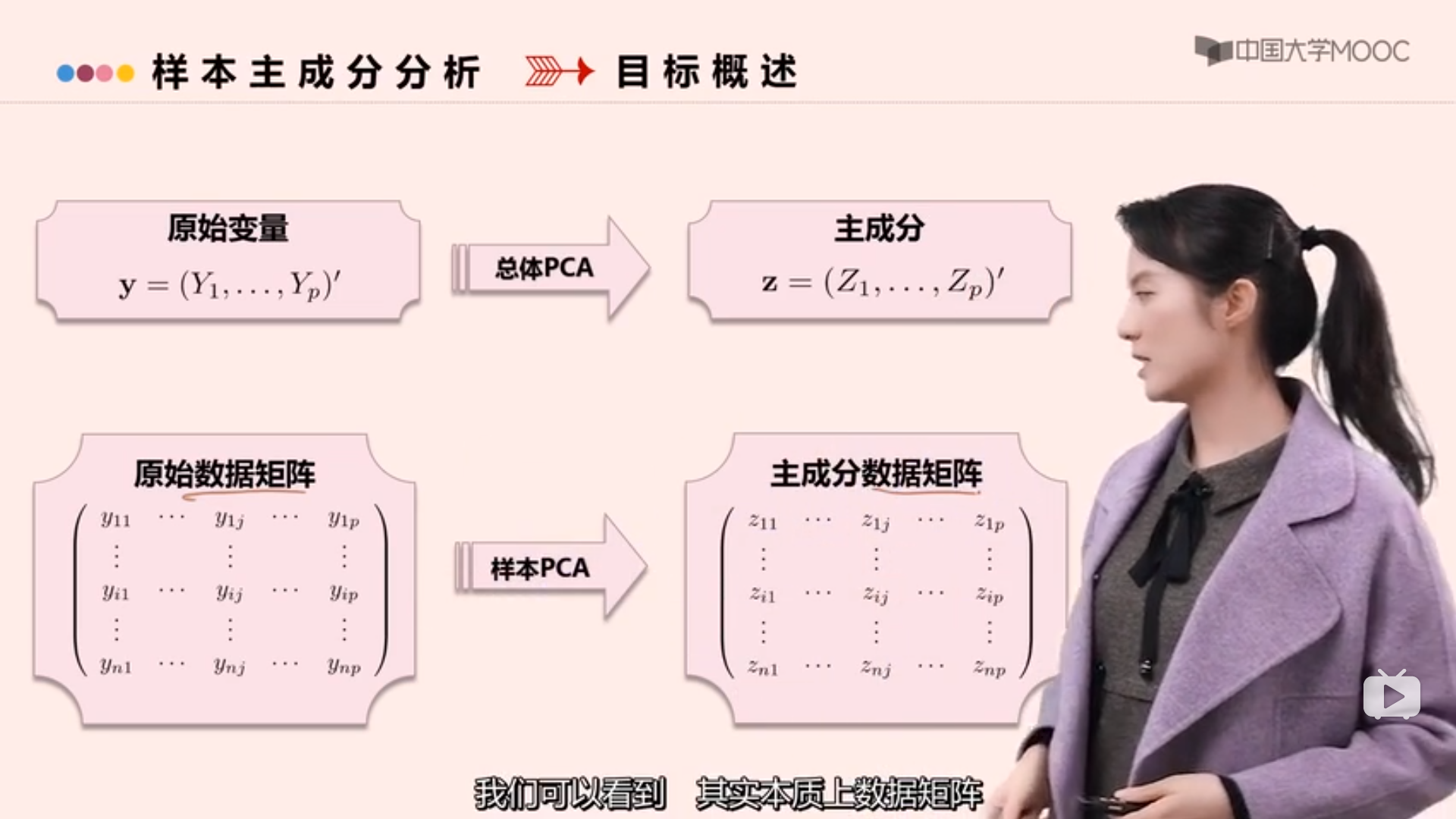


总体主成分分析中,利用相关系数矩阵构造主成分的结论可以类似的推广到样本主成分分析。
主成分个数的选择
点击查看【bilibili】
百分比截点法(Percentage cutoff):使用一定数目的主成分来反应足够比例(比如80%)的总方差。
平均截点法(Average cutoff):使用特征值大于平均特征值的主成分(很多软件包的默认准则)
对使用相关矩阵做的主成分分析来说,这个平均值为1
当数据能够在较小的维度下被很好的归纳时,特征值可以明显的分为‘大特征值’和‘小特征值’
R语言应用示例
第七章 因子分析
因子分析简介
载荷估计方法
主成分法
其他方法
估计因子得分
因子旋转
因子旋转的理解
正交旋转和斜交旋转
R语言实例
第八章 聚类分析
聚类分析概述
直观理解
在分类分析中,个体的类别标签固有存在,只是对于新观测个体暂时未知,分类过程旨在根据其特征预测类别,后续可知是否预测准确,故属于有监督学习。
在聚类分析中,类别的个数及个体标签本身并不存在,只是根据个体特征的相似性形成“合理”的聚集,并无“正确答案”参考,故其属于无监督学习(unsupervised learning)
相似程度的度量
合理的聚类方式应使得同一族群内的观测尽可能的“相似”,但不同族群之间有明显区分。
“距离”越小越相似。
层次聚类
简介
点击查看【bilibili】
考虑所有的群组组合几乎无法实现,所以一种常见的聚类方法为层次聚类、系统聚类(Hierarchical Clustering)
凝聚法
凝聚法(Agglomeration clustering)由单个个体开始,逐步合并最“相似”的个体,直到所有个体都合并为一个族群。
分离法(Divisive clustering)即为凝聚法的相反方向。
层次聚类过程的结果可以利用图表展示为系统树图(Dendrogram),用来展示层次聚类的每一个步骤及其结果,包括合并图群带来的距离的变化。
层次聚类的类型
点击查看【bilibili】
简单连接(Single linkage)/最近邻方法(Nearest neighbor method)定义族群间的距离为两族群中相隔最近的两个体间的距离。
完全连接(Complete linkage)/最远邻方法(Farthest neighbor method)以两组别中最远个体之间的距离来定义族群之间的距离。