2020年江西省南昌市高考数学三模试卷(理科)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)已知(1+i)z=i(i为虚数单位),在复平面内,复数z的共轭复数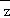 对应的点在( )
对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
2.(5分)设集合A={x||x﹣a|=1},B={﹣1,0,b}(b>0),若A⊆B,则对应的实数(a,b)有( )
A.1对 B.2对 C.3对 D.4对
3.(5分)为了普及环保知识,增强环保意识,某中学随机抽取30名学生参加环保知识竞赛,得分(10分制)的频数分布表如表:
| 得分 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|
| 频数 | 2 | 3 | 10 | 6 | 3 | 2 | 2 | 2 |
设得分的中位数为me,众数为m_0,平均数为_x,则( )
A.me=m_0=_x B.me=m_0<_x C.me<m_0<_x D.m_0<_me<x
4.(5分)某几何体的三视图如图所示,则该几何体的体积为( )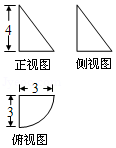
A.3π B.9π C.12π D.36π
5.(5分)在△ABC中,D为线段AB上一点,且BD=3AD,若 ,则
,则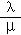 =( )
=( )
A.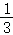 B.3 C.
B.3 C.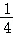 D.4
D.4
6.(5分)在△ABC中,角A,B,C所对应的边分别为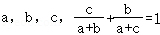 ,则下列说法不一定成立的是( )
,则下列说法不一定成立的是( )
A.△ABC可能为正三角形 B.角A,B,C为等差数列
C.角B可能小于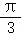 D.角B+C为定值
D.角B+C为定值
7.(5分)已知函数f(x)=2sin2ωx(ω>0)的最小正周期为π,若将其图象沿x轴向右平移m(m>0)个单位,所得图象关于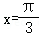 对称,则实数m的最小值为( )
对称,则实数m的最小值为( )
A.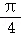 B.
B.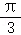 C.
C. D.π
D.π
8.(5分)函数f(x)=(x﹣ )cosx(﹣π≤x≤π且x≠0)的图象可能为( )
)cosx(﹣π≤x≤π且x≠0)的图象可能为( )
A.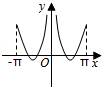 B.
B.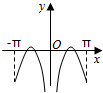
C.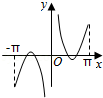 D.
D.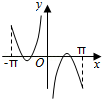
9.(5分)甲、乙两人进行象棋比赛,采取五局三胜制(不考虑平局,先赢得三场的人为获胜者,比赛结束).根据前期的统计分析,得到甲在和乙的第一场比赛中,取胜的概率为0.5,受心理方面的影响,前一场比赛结果会对甲的下一场比赛产生影响,如果甲在某一场比赛中取胜,则下一场取胜率提高0.1,反之,降低0.1.则甲以3:1取得胜利的概率为( )
A.0.162 B.0.18 C.0.168 D.0.174
10.(5分)已知双曲线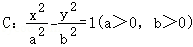 的左、右焦点分别为F_1,_F_2,点_M在C的右支上,MF_1与_y轴交于点A,△MAF_2的内切圆与边_AF_2切于点_B.若|F_1_F_2|=4|_AB|,则C的渐近线方程为( )
的左、右焦点分别为F_1,_F_2,点_M在C的右支上,MF_1与_y轴交于点A,△MAF_2的内切圆与边_AF_2切于点_B.若|F_1_F_2|=4|_AB|,则C的渐近线方程为( )
A.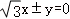 B.
B.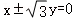 C.2x±y=0 D.x±2y=0
C.2x±y=0 D.x±2y=0
11.(5分)将正整数20分解成两个正整数的乘积有1×20,2×10,4×5三种,其中4×5是这三种分解中两数差的绝对值最小的.我们称4×5为20的最佳分解.当p×q(p≤q且p,q∈N+)是正整数n的最佳分解时,定义函数f(n)=q﹣p,则数列{f(3n)}(n∈N+)的前100项和S_100为( )
A.350+1 B.350﹣1 C.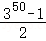 D.
D.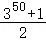
12.(5分)已知函数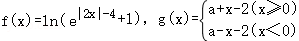 ,若存在_a∈[n,n+1](n∈Z)使得方程f(x)=g(x)有四个实根.则n的最大值为( )
,若存在_a∈[n,n+1](n∈Z)使得方程f(x)=g(x)有四个实根.则n的最大值为( )
A.2 B.1 C.0 D.﹣1
二.填空题:本题共4小题,每小题5分共20分.
13.(5分)执行如图所示的框图程序,输出的结果S= .
14.(5分)已知函数 ,则m,n,p的大小关系是 .
,则m,n,p的大小关系是 .
15.(5分)已知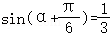 ,则
,则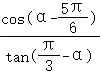 = .
= .
16.(5分)已知长方体ABCD﹣A_1_B_1_C_1_D_1,_AB= ,已知P是矩形ABCD内一动点,PA_1与平面_ABCD所成角为
,已知P是矩形ABCD内一动点,PA_1与平面_ABCD所成角为 ,设P点形成的轨迹长度为α,则tanα= ;当C_1_P的长度最短时,三棱锥D_1﹣_DPC的外接球的表面积为 .
,设P点形成的轨迹长度为α,则tanα= ;当C_1_P的长度最短时,三棱锥D_1﹣_DPC的外接球的表面积为 .
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答;第22、23题为选考题,考生根据要求作答.(一)必考题:共60分
17.(12分)已知数列{a__n}中,a_1=2,_anan+1=2pn+1(p为常数).
(Ⅰ)若﹣a_1,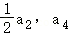 成等差数列,求_p的值;
成等差数列,求_p的值;
(Ⅱ)是否存在p,使得{a__n}为等比数列?若存在,求{a__n}的前n项和Sn;若不存在,请说明理由.
18.(12分)三棱柱ABC﹣A_1_B_1_C_1中,_AB=2,BC=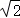 ,AC=2,四边形ABB_1_A_1为菱形,且∠_ABB_1=60_o,AC⊥CC_1.
,AC=2,四边形ABB_1_A_1为菱形,且∠_ABB_1=60_o,AC⊥CC_1.
(Ⅰ)求证:平面_ABB_1_A_1⊥平面_BB_1_C_1_C;
(Ⅱ)求BB_1与平面_ABC的夹角正弦值.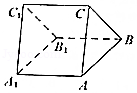
19.(12分)在“挑战不可能”的电视节目上,甲、乙、丙三个人组成的解密团队参加一项解密挑战活动,规则是由密码专家给出题目,然后由3个人依次出场解密,每人限定时间是1分钟内,否则派下一个人.3个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲100次的测试记录,绘制了如下的频率分布直方图.
(1)若甲解密成功所需时间的中位数为47,求a、b的值,并求出甲在1分钟内解密成功的频率;
(2)在“挑战不可能”节目上由于来自各方及自身的心理压力,甲,乙,丙解密成功的概率分别为Pn=P_1(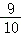 )_n﹣1+
)_n﹣1+ (n=1,2,3),其中Pi表示第i个出场选手解密成功的概率,并且P_1定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
(n=1,2,3),其中Pi表示第i个出场选手解密成功的概率,并且P_1定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
①求该团队挑战成功的概率;
②该团队以_Pi从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人员数目X的分布列与数学期望.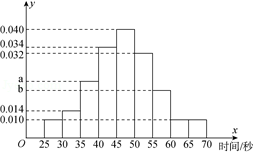
20.(12分)在直角坐标系xOy上取两个定点A_1(﹣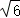 ,0),_A_2(
,0),_A_2(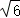 ,0),再取两个动点_N_1(0,_m),N_2(0,_n),且mn=2.
,0),再取两个动点_N_1(0,_m),N_2(0,_n),且mn=2.
(Ⅰ)求直线A_1_N_1与_A_2_N_2交点_M的轨迹C的方程;
(Ⅱ)过R(3,0)的直线与轨迹C交于P,Q,过P作PN⊥x轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若 =λ
=λ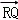 (λ>1),求证:
(λ>1),求证: =λ
=λ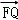 .
.
21.(12分)已知函数 (a∈R).
(a∈R).
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)当a=﹣1时,对任意的x_1,_x_2∈(0,+∞),且_x_1≠_x_2,都有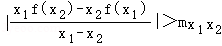 ,求实数_m的取值范围.
,求实数_m的取值范围.
(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]
22.(10分)在极坐标系中,曲线C:ρ=4cosθ,以极点O为旋转中心,将曲线C逆时针旋转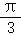 得到曲线C′.
得到曲线C′.
(Ⅰ)求曲线C’的极坐标方程;
(Ⅱ)求曲线C与曲线C′的公共部分面积.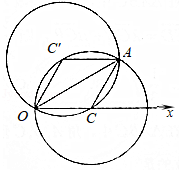
[选修4-5:不等式选讲]
23.已知f(x)=k|x|+|x﹣1|.
(Ⅰ)若k=2,解不等式f(x)≤5.
(Ⅱ)若关于x的不等式f(x)≤|x+1|+|2x﹣2|的充分条件是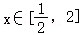 ,求k的取值范围.
,求k的取值范围.
2020年江西省南昌市高考数学三模试卷(理科)
参考答案与试题解析
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)已知(1+i)z=i(i为虚数单位),在复平面内,复数z的共轭复数 对应的点在( )
对应的点在( )
A.第一象限 B.第二象限 C.第三象限 D.第四象限
【考点】A4:复数的代数表示法及其几何意义.菁优网版权所有
【分析】把已知等式变形,利用复数代数形式的乘除运算化简,求出 的坐标得答案.
的坐标得答案.
【解答】解:由(1+i)z=i,
得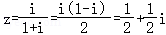 ,
,
∴复数z的共轭复数 对应的点是
对应的点是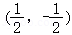 ,在第四象限.
,在第四象限.
故选:D.
【点评】本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.
2.(5分)设集合A={x||x﹣a|=1},B={﹣1,0,b}(b>0),若A⊆B,则对应的实数(a,b)有( )
A.1对 B.2对 C.3对 D.4对
【考点】18:集合的包含关系判断及应用.菁优网版权所有
【分析】解方程得集合A有两元素,由A⊆B得A中元素属于B,可解出a,b.
【解答】解:∵集合A={x||x﹣a|=1}={a﹣1,a+1}⊆{﹣1,0,b}(b>0),若a≤0,则a﹣1=﹣1,即a=0,所以b=1;
若a>0,a﹣1=﹣1或a﹣1=0,则a=1,所以b=2,
则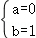 或
或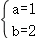 则对应的实数(a,b)有2对.
则对应的实数(a,b)有2对.
故选:B.
【点评】本题考查的知识点是集合的包含关系及应用,属于基础题.
3.(5分)为了普及环保知识,增强环保意识,某中学随机抽取30名学生参加环保知识竞赛,得分(10分制)的频数分布表如表:
| 得分 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|
| 频数 | 2 | 3 | 10 | 6 | 3 | 2 | 2 | 2 |
设得分的中位数为me,众数为m_0,平均数为_x,则( )
A.me=m_0=_x B.me=m_0<_x C.me<m_0<_x D.m_0<_me<x
【考点】BB:众数、中位数、平均数.菁优网版权所有
【分析】由频率分步表求出众数、中位数和平均数,比较即可.
【解答】解:由图知,众数是m_0=5;
中位数是第15个数与第16个数的平均值,
由图知将数据从大到小排第15 个数是5,第16个数是6,
所以中位数是_me=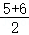 =5.5;
=5.5;
平均数是x=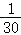 ×(2×3+3×4+10×5+6×6+3×7+2×8+2×9+2×10)≈6;
×(2×3+3×4+10×5+6×6+3×7+2×8+2×9+2×10)≈6;
∴m_0<_me<x.
故选:D.
【点评】本题考查了求出一组数据的众数、中位数、平均值的应用问题,是基础题.
4.(5分)某几何体的三视图如图所示,则该几何体的体积为( )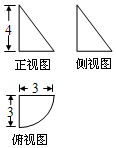
A.3π B.9π C.12π D.36π
【考点】L!:由三视图求面积、体积.菁优网版权所有
【分析】由三视图还原原几何体,可知该几何体为一个圆锥的四分之一,其中圆锥的底面半径为3,高为4,再由圆锥体积公式求解.
【解答】解:由三视图还原原几何体如图,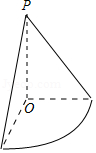
该几何体为一个圆锥的四分之一,其中圆锥的底面半径为3,高为4.
∴该几何体的体积为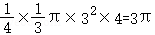 .
.
故选:A.
【点评】本题考查由三视图求面积、体积,关键是由三视图还原原几何体,是中档题.
5.(5分)在△ABC中,D为线段AB上一点,且BD=3AD,若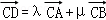 ,则
,则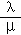 =( )
=( )
A.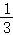 B.3 C.
B.3 C.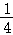 D.4
D.4
【考点】9H:平面向量的基本定理.菁优网版权所有
【分析】由已知结合向量的线性运算可分别求出λμ,从而可求.
【解答】解:因为BD=3AD,
所以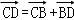 =
=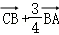 =
=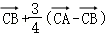 =
=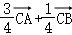 ,
,
由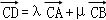 可得λ=
可得λ=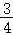 ,μ=
,μ=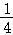 ,则
,则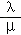 =3.
=3.
故选:B.
【点评】本题考查了平面向量的线性运算的应用及平面向量基本定理的应用.
6.(5分)在△ABC中,角A,B,C所对应的边分别为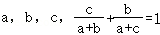 ,则下列说法不一定成立的是( )
,则下列说法不一定成立的是( )
A.△ABC可能为正三角形 B.角A,B,C为等差数列
C.角B可能小于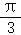 D.角B+C为定值
D.角B+C为定值
【考点】83:等差数列的性质.菁优网版权所有
【分析】化简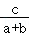 +
+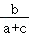 =1,利用余弦定理求出A的值,再判断选项中的命题是否正确.
=1,利用余弦定理求出A的值,再判断选项中的命题是否正确.
【解答】解:△ABC中,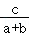 +
+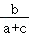 =1,
=1,
(a+c)c+(a+b)b=(a+b)(a+c),
c_2+_b_2﹣_a_2=_cb,
cosA=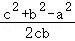 =
=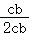 =
=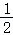 ,
,
A∈(0,π),
A= ,
,
B+C=2A=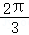 ,
,
所以B、A、C成等差数列,B错误.
当a=b=c时,△ABC是正三角形,A正确;
由B+C=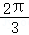 知,选项C、D正确.
知,选项C、D正确.
故选:B.
【点评】本题考查了解三角形的应用问题,也考查了分析问题解决问题的能力,是中档题.
7.(5分)已知函数f(x)=2sin2ωx(ω>0)的最小正周期为π,若将其图象沿x轴向右平移m(m>0)个单位,所得图象关于 对称,则实数m的最小值为( )
对称,则实数m的最小值为( )
A.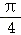 B.
B.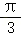 C.
C. D.π
D.π
【考点】HJ:函数y=Asin(ωx+φ)的图象变换.菁优网版权所有
【分析】先利用降幂公式将函数式化简为y=A_cos(ω_x+φ)+k的形式,然后利用图象变换的规律求出变换后的解析式,最后利用函数的最值的性质求出m的值.
【解答】解:f(x)=﹣cos2ωx+1,由其最小正周期为π,∴ω=1,所以f(x)=﹣cos2x+1,
将其图象沿x轴向右平移m(m>0)个单位,所得图象对应函数为y=﹣cos(2x﹣2m)+1,
因为其图象关于 对称,则有
对称,则有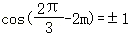 ,
,
∴ ,解得
,解得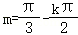 ,
,
由m>0,实数m的最小值为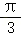 .
.
故选:B.
【点评】本题考查考生对正弦型三角函数的图象与性质(对称性、周期性、单调性)的掌握情况.考查考生对三角函数三种表征(零点、对称轴、单调性)的理解与转换.考查考生对三角函数的数形结合思想、基于三角函数的逻辑推理能力及运算求解能力.
8.(5分)函数f(x)=(x﹣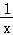 )cosx(﹣π≤x≤π且x≠0)的图象可能为( )
)cosx(﹣π≤x≤π且x≠0)的图象可能为( )
A.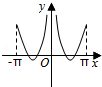 B.
B.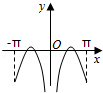
C.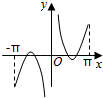 D.
D.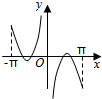
【考点】3A:函数的图象与图象的变换.菁优网版权所有
【分析】由条件可得函数f(x)为奇函数,故它的图象关于原点对称;再根据但是当x趋向于0时,f(x)>0,结合所给的选项,得出结论.
【解答】解:对于函数f(x)=(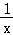 ﹣x)cosx(﹣π≤x≤π且x≠0),由于它的定义域关于原点对称,
﹣x)cosx(﹣π≤x≤π且x≠0),由于它的定义域关于原点对称,
且满足f(﹣x)=(﹣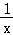 +x)cosx=﹣f(x),故函数f(x)为奇函数,故它的图象关于原点对称.
+x)cosx=﹣f(x),故函数f(x)为奇函数,故它的图象关于原点对称.
故排除A、B.
当x=π,f(x)<0,故排除C,
但是当x趋向于0时,f(x)<0,
故选:D.
【点评】本题主要考查函数的奇偶性的判断,奇函数的图象特征,函数的定义域和值域,属于中档题.
9.(5分)甲、乙两人进行象棋比赛,采取五局三胜制(不考虑平局,先赢得三场的人为获胜者,比赛结束).根据前期的统计分析,得到甲在和乙的第一场比赛中,取胜的概率为0.5,受心理方面的影响,前一场比赛结果会对甲的下一场比赛产生影响,如果甲在某一场比赛中取胜,则下一场取胜率提高0.1,反之,降低0.1.则甲以3:1取得胜利的概率为( )
A.0.162 B.0.18 C.0.168 D.0.174
【考点】CM:条件概率与独立事件.菁优网版权所有
【分析】先列出甲以3:1取得胜利的所有情况,再利用相互独立事件的乘法运算求解每种情况的概率,最后利用互斥事件概率的加法公式计算即可.
【解答】解:甲以3:1取得胜利的所有情况为:赢赢输赢,赢输赢赢,输赢赢赢,
对应的概率分别为:
0.5×0.6×0.3×0.6=0.054,
0.5×0.4×0.5×0.6=0.06,
0.5×0.4×0.5×0.6=0.06,
所以甲以3:1取得胜利的概率为:0.054+0.06+0.06=0.174.
故选:D.
【点评】本题主要考查相互独立事件的概率,互斥事件的概率,考查运算求解能力和分析问题,解决问题的能力.
10.(5分)已知双曲线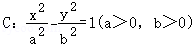 的左、右焦点分别为F_1,_F_2,点_M在C的右支上,MF_1与_y轴交于点A,△MAF_2的内切圆与边_AF_2切于点_B.若|F_1_F_2|=4|_AB|,则C的渐近线方程为( )
的左、右焦点分别为F_1,_F_2,点_M在C的右支上,MF_1与_y轴交于点A,△MAF_2的内切圆与边_AF_2切于点_B.若|F_1_F_2|=4|_AB|,则C的渐近线方程为( )
A.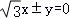 B.
B.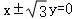 C.2x±y=0 D.x±2y=0
C.2x±y=0 D.x±2y=0
【考点】KC:双曲线的性质.菁优网版权所有
【分析】由双曲线的定义和内切圆的切线性质:圆外一点向圆引切线,则切线长相等,结合双曲线的定义,转化求解渐近线方程即可.
【解答】解:双曲线 的左、右焦点分别为F_1,_F_2,点_M在C的右支上,MF_1与_y轴交于点A,△MAF_2的内切圆与边_AF_2切于点_B.与MF_1的切点为_N,如图:设AB=n,MB=m,BF_2=_t,由双曲线的定义可知:m+2n+t﹣m﹣t=2a,可得n=a,
的左、右焦点分别为F_1,_F_2,点_M在C的右支上,MF_1与_y轴交于点A,△MAF_2的内切圆与边_AF_2切于点_B.与MF_1的切点为_N,如图:设AB=n,MB=m,BF_2=_t,由双曲线的定义可知:m+2n+t﹣m﹣t=2a,可得n=a,
若|F_1_F_2|=4|_AB|,
所以2c=4a,c=2a,则b=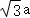 .
.
所以双曲线的渐近线方程为: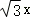 ±y=0.
±y=0.
故选:A.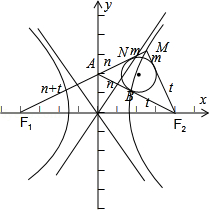
【点评】本题考查双曲线的方程和性质,主要是离心率的求法,注意运用圆的切线长相等,以及方程思想,考查运算能力,属于中档题.
11.(5分)将正整数20分解成两个正整数的乘积有1×20,2×10,4×5三种,其中4×5是这三种分解中两数差的绝对值最小的.我们称4×5为20的最佳分解.当p×q(p≤q且p,q∈N+)是正整数n的最佳分解时,定义函数f(n)=q﹣p,则数列{f(3n)}(n∈N+)的前100项和S_100为( )
A.350+1 B.350﹣1 C.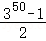 D.
D.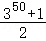
【考点】8E:数列的求和.菁优网版权所有
【分析】先写出数列{_f(3n)}(n∈N+)的前几项,根据前几项归纳出:f(32k﹣1)=3k﹣3k﹣1=2×3k﹣1,f(32k)=3k﹣3k=0,再求出其前100项和.
【解答】解:根据题意,知:f(3)=3﹣1=2,f(32)=3﹣3=0,f(33)=32﹣3=6,f(34)=32﹣32=0,…,f(32k﹣1)=3k﹣3k﹣1=2×3k﹣1,
f(32k)=3k﹣3k=0.
∴数列{f(3n)}(n∈N+)的前100项和S_100为2×30+0+2×31+0+…+2×349+0=2(30+31+32+…+349)=2× =350﹣1.
=350﹣1.
故选:_B.
【点评】本题主要考查等比数列、及其数列的求和,属于中档题.
12.(5分)已知函数 ,若存在a∈[n,n+1](n∈Z)使得方程f(x)=g(x)有四个实根.则n的最大值为( )
,若存在a∈[n,n+1](n∈Z)使得方程f(x)=g(x)有四个实根.则n的最大值为( )
A.2 B.1 C.0 D.﹣1
【考点】53:函数的零点与方程根的关系.菁优网版权所有
【分析】依题意,转化可得函数 与直线y=a有且仅有四个不同的交点,且易发现函数F(x)为偶函数,利用导数研究函数F(x)的性质,作出函数图象,观察图象可得实数a的取值范围,进而得到n的最大值.
与直线y=a有且仅有四个不同的交点,且易发现函数F(x)为偶函数,利用导数研究函数F(x)的性质,作出函数图象,观察图象可得实数a的取值范围,进而得到n的最大值.
【解答】解:令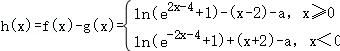 ,则
,则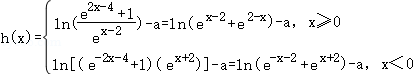 ,
,
依题意,函数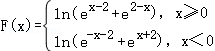 与直线y=a有且仅有四个不同的交点,
与直线y=a有且仅有四个不同的交点,
易知函数F(x)为偶函数,故先研究x≥0时的情况,
当x≥0时,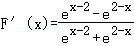 ,令F′(x)<0,解得0≤x<2,令F′(x)>0,解得x>2,
,令F′(x)<0,解得0≤x<2,令F′(x)>0,解得x>2,
故函数F(x)在(0,2)上单调递减,在(2,+∞)上单调递增,且F(x)极小值=F(2)=ln_2,
由偶函数的对称性,可作出函数_F(x)的图象,如下图所示,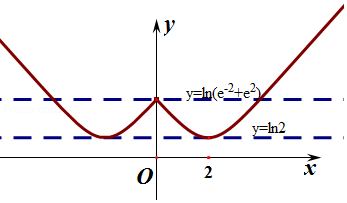
由图可知,a∈(ln_2,_ln(e﹣2+e_2)),又0<_ln_2<1,2<_ln(e﹣2+e_2)<3,
∴_n的最大值为2.
故选:A.
【点评】本题考查函数与导数的综合运用,考查函数零点与方程根的关系,考查转化思想与数形结合思想,将问题转化为函数F(x)的图象与直线y=a有且仅有四个不同的交点,进而通过数形结合确定实数a的取值范围是解题的关键,属于中档题.
二.填空题:本题共4小题,每小题5分共20分.
13.(5分)执行如图所示的框图程序,输出的结果S= 5 .
【考点】EF:程序框图.菁优网版权所有
【分析】模拟程序的运行过程可知:该程序的功能是利用循环结构计算并输出变量s=0﹣1+2﹣3+…+10的值,分析循环中各变量值的变化情况,可得答案.
【解答】解:模拟程序的运行,可得该程序的功能是利用循环结构计算并输出变量s=0﹣1+2﹣3+…+10的值,
可得s=0﹣1+2﹣3+…+10=(2+4+…+10)﹣(1+3+…+9)=5.
故答案为:5.
【点评】本题主要考查伪代码(算法语句)的应用,属于基础题.
14.(5分)已知函数 ,则m,n,p的大小关系是 p>m>n .
,则m,n,p的大小关系是 p>m>n .
【考点】3N:奇偶性与单调性的综合.菁优网版权所有
【分析】根据函数奇偶性和单调性之间的关系,即可得到结论.
【解答】解:∵f(x)=2|x|+x_2,则_f(﹣x)=2|﹣x|+(﹣x)2=f(x),即f(x)为偶函数,
因为x>0时,f(x)=2x+x_2单调递增,
_m=f(log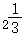 )=f(log23),n=f(0.7﹣0.1),p=f(log425)=f(log25),
)=f(log23),n=f(0.7﹣0.1),p=f(log425)=f(log25),
因为log25>2>log23>1>7﹣0.1>0,
故p>m>n
故答案为:p>m>n
【点评】本题主要考查函数值的大小比较,根据函数奇偶性和单调性之间的关系是解决本题的关键.
15.(5分)已知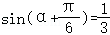 ,则
,则 =
= 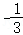 .
.
【考点】GP:两角和与差的三角函数.菁优网版权所有
【分析】直接利用三角函数关系式的恒等变换和诱导公式的应用求出结果.
【解答】解:已知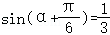 .故:
.故: =
=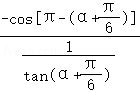 =
= =﹣
=﹣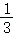 .
.
故答案为: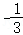 .
.
【点评】本题考查的知识要点:三角函数关系式的恒等变换,诱导公式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.
16.(5分)已知长方体ABCD﹣A_1_B_1_C_1_D_1,_AB=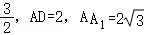 ,已知P是矩形ABCD内一动点,PA_1与平面_ABCD所成角为
,已知P是矩形ABCD内一动点,PA_1与平面_ABCD所成角为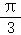 ,设P点形成的轨迹长度为α,则tanα= ﹣3
,设P点形成的轨迹长度为α,则tanα= ﹣3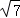 ;当C_1_P的长度最短时,三棱锥D_1﹣_DPC的外接球的表面积为 17π .
;当C_1_P的长度最短时,三棱锥D_1﹣_DPC的外接球的表面积为 17π .
【考点】LG:球的体积和表面积.菁优网版权所有
【分析】因为PA_1与平面_ABCD所成角θ为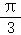 ,所以可得AP=2,即P点的轨迹为以A为圆心,以2为半径的圆与矩形ABCD的交点即
,所以可得AP=2,即P点的轨迹为以A为圆心,以2为半径的圆与矩形ABCD的交点即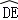 ,由矩形的边长可得
,由矩形的边长可得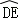 的值,进而求出它的正切值,当C_1_P的长度最短时,而C_1_P=
的值,进而求出它的正切值,当C_1_P的长度最短时,而C_1_P=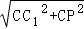 ,所以当CP最小时,C_1_P最小,而当A,P,C_1三点共线时,_CP最小,求出CP的值,进而由余弦定理求出DP,求出三角形DCP的外接圆的半径,由DD_1⊥面_CDP,所以三棱锥D_1﹣_DCP的外接球的球心为过底面三角形DCP的外接圆的圆心的垂线与中截面的交点,由外接球的半径,和高的一半,由勾股定理可得R的值,进而求出外接球的表面积.
,所以当CP最小时,C_1_P最小,而当A,P,C_1三点共线时,_CP最小,求出CP的值,进而由余弦定理求出DP,求出三角形DCP的外接圆的半径,由DD_1⊥面_CDP,所以三棱锥D_1﹣_DCP的外接球的球心为过底面三角形DCP的外接圆的圆心的垂线与中截面的交点,由外接球的半径,和高的一半,由勾股定理可得R的值,进而求出外接球的表面积.
【解答】解:在长方体的底面矩形ABCD内一动点P,连接AP,
因为PA_1与平面_ABCD所成角θ为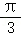 ,AA_1=2
,AA_1=2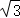 ,所以tanθ=
,所以tanθ=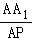 =
= =
=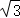 ,所以_AP=2,
,所以_AP=2,
所以P点的轨迹为以A为圆心,以2为半径的圆,与底面矩形BC的交点为E,D,
即P的轨迹为圆弧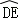 ,连接AE,
,连接AE,
在△ABE中,cos∠EAB= =
= =
=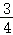 ,所以sin∠DAE=cos∠EAB=
,所以sin∠DAE=cos∠EAB=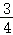 ,所以arcsin∠DAE=
,所以arcsin∠DAE=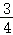 ,
,
所以α=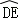 =2•∠DAE,可得α为钝角,
=2•∠DAE,可得α为钝角,
所以sinα=sin(2arcsin∠DAE)=2•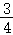
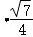 =
= ,∴cosα=﹣
,∴cosα=﹣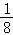 ,
,
所以tanα=﹣3 ;
;
当C_1_P的长度最短时,而C_1_P= ,所以当CP最小时,C_1_P最小,
,所以当CP最小时,C_1_P最小,
而当A,P,C_1三点共线时,_CP=AC﹣AP=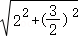 ﹣2=
﹣2= 最小,
最小,
连接DP,由于cos∠DCP=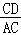 =
=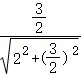 =
=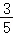 ,
,
所以在三角形CDP中,由余弦定理可得DP=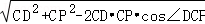 =
=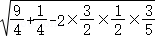 =
=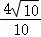 ,
,
而sin∠DCP=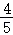 ,设三角形CDP的外接圆的半径为r,则2r=
,设三角形CDP的外接圆的半径为r,则2r=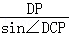 =
=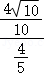 =
=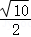 ,所以r=
,所以r=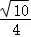 ,
,
由DD_1⊥面_CDP,所以三棱锥D_1﹣_DCP的外接球的球心为过底面三角形DCP的外接圆的圆心的垂线与中截面的交点,
设外接球的半径为R,则R_2=_r_2+(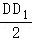 )2=
)2=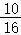 +3=
+3=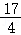 ,
,
所以外接球的表面积_S=4πR_2=17π.
故答案为:﹣3 ,17π.
,17π.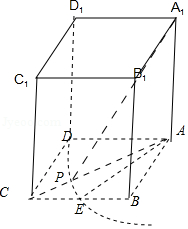
【点评】本题考查求点的轨迹,及三棱锥的棱长与外接球的半径的关系和球的表面积公式,属于难题.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答;第22、23题为选考题,考生根据要求作答.(一)必考题:共60分
17.(12分)已知数列{_a__n}中,a_1=2,_anan+1=2pn+1(p为常数).
(Ⅰ)若﹣a_1,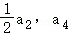 成等差数列,求_p的值;
成等差数列,求_p的值;
(Ⅱ)是否存在p,使得{a__n}为等比数列?若存在,求{a__n}的前n项和Sn;若不存在,请说明理由.
【考点】8H:数列递推式;8M:等差数列与等比数列的综合.菁优网版权所有
【分析】(Ⅰ)根据条件求出a_2和_a_4,然后由﹣_a_1,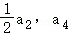 成等差数列,得到关于_p的方程,再求出p即可;
成等差数列,得到关于_p的方程,再求出p即可;
(Ⅱ)若{a__n}为等比数列,则由a_1>0,_a_2>0,可知数列的首项和公比均为正数,然后根据条件求出{_a__n}前n项和Sn即可.
【解答】解:(Ⅰ)∵anan+1=2pn+1(p为常数),∴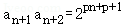
∴当n=1时, ,
,
∵a_1=2,∴ ,∴
,∴ ,
,
∴ ,
,
∵ ,∴_a_4﹣2=_a_2,
,∴_a_4﹣2=_a_2,
∴(2_p)2﹣2=2p,∴p=1.
(Ⅱ)若{a__n}为等比数列,则由a_1>0,_a_2>0,∴数列的首项和公比均为正数,
设其公比为_q,则 ,∴
,∴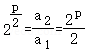 ,∴p=2,
,∴p=2,
∴a_1=2,_q=2,∴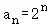 故
故 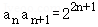 ,
,
而2pn+1=22n+1,∴p=2时,{a__n}为等比数列,
∴{a__n}的前n项和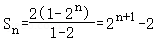 .
.
【点评】本题考查了等比数列和等差数列的性质,等比数列的前n项和公式,考查了方程思想和转化思想,属中档题.
18.(12分)三棱柱ABC﹣A_1_B_1_C_1中,_AB=2,BC= ,AC=2,四边形ABB_1_A_1为菱形,且∠_ABB_1=60_o,AC⊥CC_1.
,AC=2,四边形ABB_1_A_1为菱形,且∠_ABB_1=60_o,AC⊥CC_1.
(Ⅰ)求证:平面_ABB_1_A_1⊥平面_BB_1_C_1_C;
(Ⅱ)求BB_1与平面_ABC的夹角正弦值.
【考点】LY:平面与平面垂直;MI:直线与平面所成的角.菁优网版权所有
【分析】(Ⅰ)取BB_1的中点_O,连接AB_1,_OA,OC,由已知可得OA⊥BB_1,再由_BB_1∥_CC_1,_AC⊥CC_1,得_AC⊥BB_1,得到_BB_1⊥平面_AOC,则BB_1⊥_CO,求解三角形证明CO⊥AO.可得AO⊥平面BB_1_C_1_C,进一步得到平面ABB_1_A_1⊥平面_BB_1_C_1_C;
(Ⅱ)以O为坐标原点,建立如图所示空间直角坐标系,求出平面ABC的一个法向量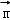 ,再求出BB_1上的单位向量
,再求出BB_1上的单位向量 .由
.由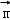 与
与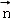 所成角的余弦值可得_BB_1与平面_ABC的夹角正弦值.
所成角的余弦值可得_BB_1与平面_ABC的夹角正弦值.
【解答】(Ⅰ)证明:取BB_1的中点_O,连接AB_1,_OA,OC,
在菱形ABB_1_A_1中,∠_ABB_1=60_o,故三角形ABB_1是等边三角形,则_OA⊥BB_1,_OB=1,OA= .
.
又BB_1∥_CC_1,_AC⊥CC_1,∴_AC⊥BB_1,
又_AO⊥BB_1,且_AO∩AC=A,∴BB_1⊥平面_AOC,则BB_1⊥_CO.
在Rt△BOC中,CO=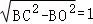 ,∴CO_2+_AO_2=_AC_2,故_CO⊥AO.
,∴CO_2+_AO_2=_AC_2,故_CO⊥AO.
又CO∩BB_1=_O,∴AO⊥平面BB_1_C_1_C.
∵AO⊂平面ABB_1_A_1,∴平面_ABB_1_A_1⊥平面_BB_1_C_1_C;
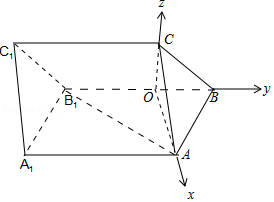
(Ⅱ)解:以O为坐标原点,建立如图所示空间直角坐标系.
则A( ,0,0),B(0,1,0),C(0,0,1),
,0,0),B(0,1,0),C(0,0,1),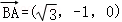 ,
,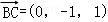 .
.
设平面ABC的一个法向量为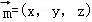 .
.
由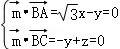 ,取x=
,取x= ,得
,得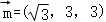 .
.
设BB_1上的单位向量为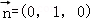 .
.
则_BB_1与平面_ABC的夹角正弦值为|cos<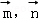 >|=
>|=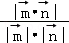 =
= .
.
【点评】本题考查平面与平面垂直的判定,考查空间想象能力与思维能力,训练了利用空间向量求解空间角,是中档题.
19.(12分)在“挑战不可能”的电视节目上,甲、乙、丙三个人组成的解密团队参加一项解密挑战活动,规则是由密码专家给出题目,然后由3个人依次出场解密,每人限定时间是1分钟内,否则派下一个人.3个人中只要有一人解密正确,则认为该团队挑战成功,否则挑战失败.根据甲以往解密测试情况,抽取了甲100次的测试记录,绘制了如下的频率分布直方图.
(1)若甲解密成功所需时间的中位数为47,求a、b的值,并求出甲在1分钟内解密成功的频率;
(2)在“挑战不可能”节目上由于来自各方及自身的心理压力,甲,乙,丙解密成功的概率分别为Pn=P_1(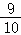 )_n﹣1+
)_n﹣1+ (n=1,2,3),其中Pi表示第i个出场选手解密成功的概率,并且P_1定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
(n=1,2,3),其中Pi表示第i个出场选手解密成功的概率,并且P_1定义为甲抽样中解密成功的频率代替,各人是否解密成功相互独立.
①求该团队挑战成功的概率;
②该团队以_Pi从小到大的顺序按排甲、乙、丙三个人上场解密,求团队挑战成功所需派出的人员数目X的分布列与数学期望.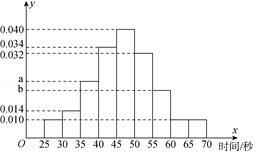
【考点】CG:离散型随机变量及其分布列;CH:离散型随机变量的期望与方差.菁优网版权所有
【分析】(1)由甲解密成功所需时间的中位数为47,利用频率分布直方图的性质能求出a,b,由此能求出甲在1分钟内解密成功的频率.
(2)①由题意及(1)可知第一个出场选手解密成功的概率为p_1=0.9,第二个出场选手解密成功的概率为_p_2=0.9×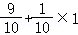 =0.91,第三个出场选手解密成功的概率为_p_3=0.9×
=0.91,第三个出场选手解密成功的概率为_p_3=0.9× =0.929,由此能求出该团队挑战成功的概率.
=0.929,由此能求出该团队挑战成功的概率.
②根据题意知_X的可能取值为1,2,3,分别求出相应的概率,由此能求出团队挑战成功所需派出的人员数目X的分布列和E(X).
【解答】解:(1)甲解密成功所需时间的中位数为47,
∴0.01×5+0.014×5+b×5+0.034×5+0.04×(47﹣45)=0.5,
解得b=0.026,
∴0.04×3+0.032×5+a×5+0.010×10=0.5.
解得a=0.024.
∴甲在1分钟内解密成功的频率是f=1﹣0.01×10=0.9.
(2)①由题意及(1)可知第一个出场选手解密成功的概率为p_1=0.9,
第二个出场选手解密成功的概率为_p_2=0.9×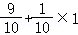 =0.91,
=0.91,
第三个出场选手解密成功的概率为_p_3=0.9× =0.929,
=0.929,
∴该团队挑战成功的概率为_p=0.9+0.1×0.91+0.1×0.09×0.929=0.999361.
②由①知按Pi从小到大的顺序的概率分别为p_1,_p_2,_p_3,
根据题意知_X的可能取值为1,2,3,
则P(X=1)=0.9,
P(X=2)=(1﹣0.9)×0.91=0.091,
P(X=3)=(1﹣0.9)(1﹣0.91)=0.009,
∴团队挑战成功所需派出的人员数目X的分布列为:
| X | 1 | 2 | 3 |
|---|---|---|---|
| P | 0.9 | 0.091 | 0.009 |
E(X)=1×0.9+2×0.091+3×0.009=1.109.
【点评】本题考查概率、离散型随机变量的分布列、数学期望的求法,考查频率分布直方图、互斥事件概率加法公式和相互独立事件概率加法公式等基础知识,考查运算求解能力,是中档题.
20.(12分)在直角坐标系xOy上取两个定点A_1(﹣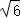 ,0),_A_2(
,0),_A_2(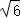 ,0),再取两个动点_N_1(0,_m),N_2(0,_n),且mn=2.
,0),再取两个动点_N_1(0,_m),N_2(0,_n),且mn=2.
(Ⅰ)求直线A_1_N_1与_A_2_N_2交点_M的轨迹C的方程;
(Ⅱ)过R(3,0)的直线与轨迹C交于P,Q,过P作PN⊥x轴且与轨迹C交于另一点N,F为轨迹C的右焦点,若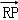 =λ
=λ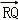 (λ>1),求证:
(λ>1),求证: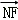 =λ
=λ .
.
【考点】J3:轨迹方程.菁优网版权所有
【分析】(I)由直线方程的点斜式列出A_1_N_1和_A_2_N_2的方程,联解并结合_mn=2化简整理得方程,再由N_1、_N_2不与原点重合,可得直线_A_1_N_1与_A_2_N_2交点的轨迹_C的方程;
(II)设l:x=ty+3,代入椭圆方程消去x,得(3+t_2)_y_2+6_ty+3=0,利用分析法进行证明.
【解答】(I)解:依题意知直线A_1_N_1的方程为:_y= (x+
(x+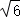 )…①;
)…①;
直线A_2_N_2的方程为:_y=﹣ (x﹣
(x﹣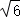 )…②
)…②
设Q(x,y)是直线A_1_N_1与_A_2_N_2交点,①、②相乘,得_y_2=﹣ (_x_2﹣6)
(_x_2﹣6)
由_mn=2整理得: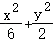 =1
=1
∵N_1、_N_2不与原点重合,可得点_A_1,_A_2不在轨迹_M上,
∴轨迹C的方程为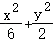 =1(x≠±
=1(x≠± ).
).
(Ⅱ)证明:设l:x=ty+3,代入椭圆方程消去x,得(3+t_2)_y_2+6_ty+3=0.
设P(x_1,_y_1),_Q(x_2,_y_2),_N(x_1,﹣_y_1),可得_y_1+_y_2=﹣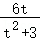 且_y_1_y_2=
且_y_1_y_2=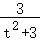 ,
, =λ
=λ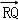 ,可得(_x_1﹣3,_y_1)=λ(_x_2﹣3,_y_2),∴_x_1﹣3=λ(_x_2﹣3),_y_1=λ_y_2,
,可得(_x_1﹣3,_y_1)=λ(_x_2﹣3,_y_2),∴_x_1﹣3=λ(_x_2﹣3),_y_1=λ_y_2,
证明 =λ
=λ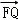 ,只要证明(2﹣_x_1,_y_1)=λ(_x_2﹣2,_y_2),∴2﹣_x_1=λ(_x_2﹣2),
,只要证明(2﹣_x_1,_y_1)=λ(_x_2﹣2,_y_2),∴2﹣_x_1=λ(_x_2﹣2),
只要证明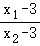 =﹣
=﹣ ,只要证明2_t_2_y_1_y_2+_t(y_1+_y_2)=0,
,只要证明2_t_2_y_1_y_2+_t(y_1+_y_2)=0,
由_y_1+_y_2=﹣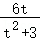 且_y_1_y_2=
且_y_1_y_2=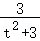 ,代入可得2_t_2_y_1_y_2+_t(y_1+_y_2)=0,
,代入可得2_t_2_y_1_y_2+_t(y_1+_y_2)=0,
∴ =λ
=λ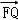 .
.
【点评】本题着重考查了动点轨迹的求法、椭圆的标准方程与简单几何性质、直线与圆锥曲线的位置关系和一元二次方程根与系数的关系等知识,属于中档题.
21.(12分)已知函数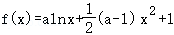 (_a∈R).
(_a∈R).
(Ⅰ)讨论f(x)的单调性;
(Ⅱ)当a=﹣1时,对任意的x_1,_x_2∈(0,+∞),且_x_1≠_x_2,都有 ,求实数_m的取值范围.
,求实数_m的取值范围.
【考点】6B:利用导数研究函数的单调性;6E:利用导数研究函数的最值.菁优网版权所有
【分析】(Ⅰ)求出导函数,通过①当a≥1时,②当0<a<1时,③当a≤0时,判断导函数的符号,判断函数的单调性即可.
(Ⅱ)当a=﹣1时,f(x)=﹣lnx﹣x_2+1,不妨设0<_x_1<_x_2,则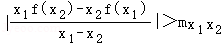 等价于
等价于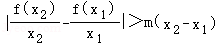 ,考察函数
,考察函数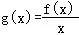 ,求出导函数,令
,求出导函数,令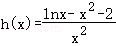 ,再求解导函数,判断函数的单调性.求出函数的最值,说明_g(x)在(0,+∞)上单调递减.得到g(x_1)+_mx_1>_g(x_2)+_mx_2恒成立,设φ(_x)=g(x)+mx,则φ(x)在(0,+∞)上恒为单调递减函数,然后转化求解m的范围即可.
,再求解导函数,判断函数的单调性.求出函数的最值,说明_g(x)在(0,+∞)上单调递减.得到g(x_1)+_mx_1>_g(x_2)+_mx_2恒成立,设φ(_x)=g(x)+mx,则φ(x)在(0,+∞)上恒为单调递减函数,然后转化求解m的范围即可.
【解答】解:(Ⅰ) (x>0).
(x>0).
①当a≥1时,f‘(x)>0,f(x)在(0,+∞)上单调递增;
②当0<a<1时,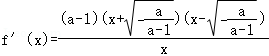 ,
,
所以当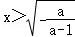 时,f‘(x)<0,当0<x<
时,f‘(x)<0,当0<x<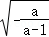 时,f‘(x)>0,
时,f‘(x)>0,
所以f(x)在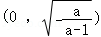 上单调递增,在
上单调递增,在 上单调递减;
上单调递减;
③当a≤0时,f‘(x)<0,f(x)在(0,+∞)上单调递减,
(Ⅱ)当a=﹣1时,f(x)=﹣lnx﹣x_2+1,不妨设0<_x_1<_x_2,
则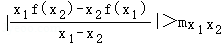 等价于
等价于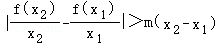 ,考察函数
,考察函数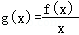 ,得
,得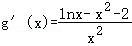 ,
,
令 ,
,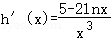 ,则
,则 时,_h‘(x)>0,
时,_h‘(x)>0,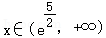 时,h‘(x)<0,所以h(x)在区间
时,h‘(x)<0,所以h(x)在区间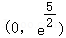 上是单调递增函数,
上是单调递增函数,
在区间 上是单调递减函数.故
上是单调递减函数.故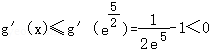 ,
,
所以g(x)在(0,+∞)上单调递减.
从而g(x_1)>_g(x_2),即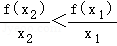 ,故
,故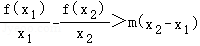 ,
,
所以 ,即_g(x_1)+_mx_1>_g(x_2)+_mx_2恒成立,
,即_g(x_1)+_mx_1>_g(x_2)+_mx_2恒成立,
设φ(_x)=g(x)+mx,则φ(x)在(0,+∞)上恒为单调递减函数,
从而φ′(x)=g′(x)+m≤0恒成立,故φ′(x)=g′(x)+m≤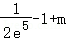 ≤0,
≤0,
故m≤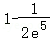 .
.
【点评】本题考查导数公式和导数运算法则以及恒成立的思想,考查考生灵活运用导数工具分析问题、解决问题的能力,综合考查考生的分类讨论思想以及逻辑推理能力、运算求解能力和推理论证能力.
(二)选考题:共10分.请考生在第22、23题中任选一题作答,如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程]
22.(10分)在极坐标系中,曲线C:ρ=4cosθ,以极点O为旋转中心,将曲线C逆时针旋转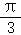 得到曲线C′.
得到曲线C′.
(Ⅰ)求曲线C’的极坐标方程;
(Ⅱ)求曲线C与曲线C′的公共部分面积.
【考点】Q4:简单曲线的极坐标方程;QH:参数方程化成普通方程.菁优网版权所有
【分析】(Ⅰ)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换.
(Ⅱ)利用三角函数关系式的恒等变换和正弦型函数的性质的应用及二次函数的性质的应用求出结果.
【解答】解:(Ⅰ)设极点(ρ,θ)旋转之后的极点为(ρ′,θ′),
故: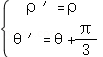 ,代入ρ=4cosθ,得到
,代入ρ=4cosθ,得到 ,得到
,得到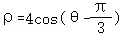 .
.
(Ⅱ)如图,两圆相交于点O和A,连接OA,AC,OC′,AC′.
由于极径没有变,旋转的角为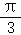 .显然四边形OC′AC为菱形,
.显然四边形OC′AC为菱形,
故∠OCA=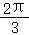 .
.
所以S=2S弓形OC′A=2(S扇形OC′A﹣S△OC′A)= .
.
【点评】本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,三角函数关系式的恒等变换,正弦型函数性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.
[选修4-5:不等式选讲]
23.已知f(x)=k|x|+|x﹣1|.
(Ⅰ)若k=2,解不等式f(x)≤5.
(Ⅱ)若关于x的不等式f(x)≤|x+1|+|2x﹣2|的充分条件是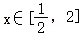 ,求k的取值范围.
,求k的取值范围.
【考点】29:充分条件、必要条件、充要条件;R5:绝对值不等式的解法.菁优网版权所有
【分析】(Ⅰ)k=2时,不等式f(x)≤5可化为2|x|+|x﹣1|≤5.然后分x<0,0≤x<1,x≥1三类去绝对值求解,取并集得答案;
(Ⅱ)由题意,关于x的不等式f(x)≤|x+1|+|2x﹣2|在 上恒成立,分离参数k,可得k≤
上恒成立,分离参数k,可得k≤ 在
在 上恒成立,再由
上恒成立,再由 ≥
≥ ,即可得到实数k的取值范围.
,即可得到实数k的取值范围.
【解答】解:(Ⅰ)若k=2,不等式f(x)≤5可化为2|x|+|x﹣1|≤5.
当x<0时,有﹣2x﹣(x﹣1)≤5,即x≥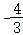 ,∴
,∴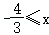 <0;
<0;
当0≤x<1时,有2x﹣(x﹣1)≤5,即x≤4,∴0≤x<1;
当x≥1时,有2x+(x﹣1)≤5,即x≤2,∴1≤x≤2.
故原不等式的解集为[﹣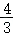 ,2];
,2];
(Ⅱ)由题意,关于x的不等式f(x)≤|x+1|+|2x﹣2|在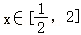 上恒成立,
上恒成立,
即k|x|≤|x+1|+|2x﹣2|﹣|x﹣1|在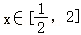 上恒成立,
上恒成立,
∴k≤ 在
在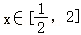 上恒成立,
上恒成立,
∵ ≥
≥ ,等号在x+1,x﹣1同号或其中一项为0时成立.
,等号在x+1,x﹣1同号或其中一项为0时成立.
∴k的取值范围是(﹣∞,2].
【点评】本题考查绝对值不等式的解法,考查分类讨论与数学转化思想方法,训练了绝对值不等式的应用,是中档题.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/6/25 20:33:44;用户:17859775485;邮箱:17859775485;学号:21682042

