2020年福建省龙岩市高考数学模拟试卷(理科)(6月份)
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)复数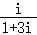 =( )
=( )
A.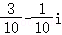 B.
B.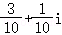 C.
C.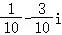 D.
D.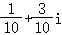
2.(5分)已知全集U=R,集合M={x||x﹣2|≤1},则∁UM=( )
A.(1,3) B.[1,3]
C.(﹣∞,1)∪(3,+∞) D.(﹣∞,1]∪[3,+∞)
3.(5分)设Sn是等差数列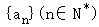 的前n项和,且a_1=1,_S_5=25,则_a_2=( )
的前n项和,且a_1=1,_S_5=25,则_a_2=( )
A.4 B.3 C.2 D.5
4.(5分)保护生态环境是每个公民应尽的职责!某校随机抽取100名同学进行“垃圾分类”的问卷测试,测试结果发现这100名同学的得分都在[50,100]内,按得分分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图,则估计这100名同学的得分的众数为( )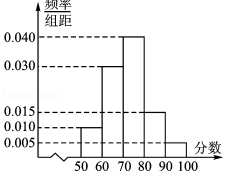
A.70 B.72.5 C.80 D.75
5.(5分)执行如图所示的程序框图,若输入_k,n的值均是0,则输出T的值为( )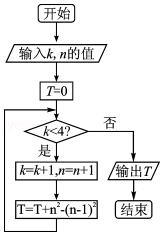
A.9 B.16 C.25 D.36
6.(5分)用数字1,2,3组成无重复数字的三位数,那么所有的三位数中是奇数的概率为( )
A.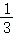 B.
B.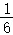 C.
C. D.
D.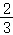
7.(5分)在矩形ABCD中,AB=3,AD=4,平面上一点P满足PA=1,PC=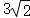 ,则
,则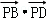 =( )
=( )
A.﹣3 B.3 C.0 D.1
8.(5分)已知函数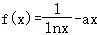 在(1,+∞)上有极值,则实数a的取值范围为( )
在(1,+∞)上有极值,则实数a的取值范围为( )
A.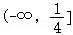 B.
B.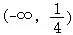 C.
C.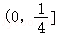 D.
D.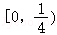
9.(5分)在三棱锥P﹣ABC中,PA⊥平面ABC,PA=2,AB=4,AC=3,∠BAC=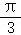 ,则三棱锥P﹣ABC的外接球的半径R=( )
,则三棱锥P﹣ABC的外接球的半径R=( )
A.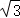 B.
B. C.
C.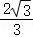 D.
D.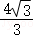
10.(5分)设A,B为双曲线Γ: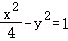 的左,右顶点,F为双曲线Γ右焦点,以原点O为圆心,|OF|为半径的圆与双曲线Γ的一条渐近线的一个交点为M,连接AM,BM,则tan∠AMB=( )
的左,右顶点,F为双曲线Γ右焦点,以原点O为圆心,|OF|为半径的圆与双曲线Γ的一条渐近线的一个交点为M,连接AM,BM,则tan∠AMB=( )
A.4 B.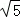 C.2 D.
C.2 D.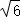
11.(5分)已知数列{a__n}满足an+1=an+a__n﹣1(n≥2),又{a__n}的前项和为Sn,若S_6=52,则_a_5=( )
A.13 B.15 C.17 D.31
12.(5分)已知抛物线_C_1: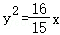 和圆_C_2:(_x﹣6)2+(y﹣1)2=1,过圆C_2上一点_P作圆的切线MN交抛物线C_1于_M,N两点,若点P为MN的中点,则切线MN的斜率k>1时的直线方程为( )
和圆_C_2:(_x﹣6)2+(y﹣1)2=1,过圆C_2上一点_P作圆的切线MN交抛物线C_1于_M,N两点,若点P为MN的中点,则切线MN的斜率k>1时的直线方程为( )
A.4x﹣3y﹣22=0 B.4x﹣3y﹣16=0
C.2x﹣y﹣11+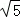 =0 D.4x﹣3y﹣26=0
=0 D.4x﹣3y﹣26=0
二、填空题:本题共4小题,每小题5分,共20分.
13.(5分)函数y=(2x_2+1)_ex在点(0,1)处的切线方程为 .
14.(5分)若实数x、y满足约束条件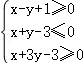 ,则z=2x﹣y的最大值为 .
,则z=2x﹣y的最大值为 .
15.(5分)一条河的两岸平行,河的宽度d=4km,一艘船从岸边A处出发到河的正对岸,已知船的速度|v_1|=10_km/h,水流速度|v_2|=2_km/h,那么行驶航程最短时,所用时间是 (h).(附: ≈2.449,精确到0.01h).
≈2.449,精确到0.01h).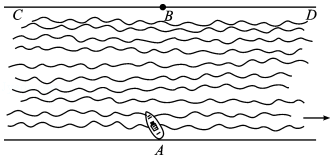
16.(5分)已知函数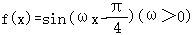 ,满足不等式
,满足不等式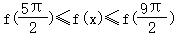 在R上恒成立,在
在R上恒成立,在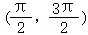 上恰好只有一个极值点,则实数ω= .
上恰好只有一个极值点,则实数ω= .
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分
17.(12分)△ABC的内角A,B,C的对边分别为a、b、c,若a+c= ,cosA=
,cosA= ,sinC=
,sinC= .
.
(1)求sinB;
(2)求△ABC的面积.
18.(12分)如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,在四边形ABCD中,∠ABC=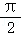 ,AB=4,BC=3,CD=
,AB=4,BC=3,CD= ,AD=2
,AD=2 ,PA=4.
,PA=4.
(1)证明:CD⊥平面PAD;
(2)求二面角B﹣PC﹣D的余弦值.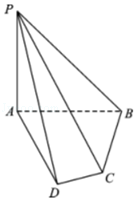
19.(12分)已知椭圆Γ: 的左,右焦点分别为F_1(
的左,右焦点分别为F_1(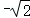 ,0),_F_2(
,0),_F_2( ,0),椭圆的左,右顶点分别为_A,B,已知椭圆Γ上一异于A,B的点P,PA,PB的斜率分别为k_1,_k_2,满足
,0),椭圆的左,右顶点分别为_A,B,已知椭圆Γ上一异于A,B的点P,PA,PB的斜率分别为k_1,_k_2,满足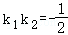 .
.
(1)求椭圆Γ的标准方程;
(2)若过椭圆Γ左顶点_A作两条互相垂直的直线AM和AN,分别交椭圆Γ于M,N两点,问x轴上是否存在一定点Q,使得∠MQA=∠NQA成立,若存在,则求出该定点Q,否则说明理由.
20.(12分)由甲乙两位同学组成一个小组参加年级组织的篮球投篮比赛,共进行两轮投篮,每轮甲乙各自独立投篮一次,并且相互不受影响,每次投中得2分,没投中得0分.已知甲同学每次投中的概率为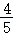 ,乙同学每次投中的概率为
,乙同学每次投中的概率为 .
.
(1)求第一轮投篮时,甲乙两位同学中至少有一人投中的概率;
(2)甲乙两位同学在两轮投篮中,记总得分为随机变量ξ,求ξ的分布列和期望.
21.(12分)(1)已知实数a>0,若关于x的不等式sinx﹣x_cos_ax≥0在0≤x≤ 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;
(2)若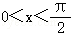 ,求证:
,求证: .
.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程](本小题满分10分)
22.(10分)在平面直角坐标系xOy中,点P是曲线C: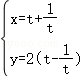 (t为参数)上的动点,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C_2的极坐标方程为:
(t为参数)上的动点,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C_2的极坐标方程为: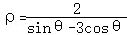 .
.
(1)求曲线_C_1,_C_2的直角坐标下普通方程;
(2)已知点_Q在曲线C_2上,求|_PQ|的最小值以及取得最小值时P点坐标.
[选修4-5:不等式选讲](本小题满分0分)
23.已知f(x)=|ax+1|,a∈R.
(1)若关于x的不等式f(x)≤3的解集为{x|﹣2≤x≤1},求实数a的值;
(2)若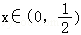 时,不等式f(x)≤2﹣|2x﹣1|恒成立.求实数a的取值范围.
时,不等式f(x)≤2﹣|2x﹣1|恒成立.求实数a的取值范围.
2020年福建省龙岩市高考数学模拟试卷(理科)(6月份)
参考答案与试题解析
一、选择题:本题共12小题,每小题5分,共60分.在每小题给出的四个选项中,只有一项是符合题目要求的.
1.(5分)复数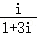 =( )
=( )
A.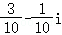 B.
B.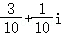 C.
C.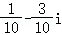 D.
D.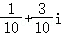
【考点】A5:复数的运算.菁优网版权所有
【分析】直接利用复数代数形式的乘除运算化简即可.
【解答】解:因为复数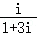 =
= =
=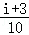 =
=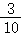
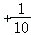 i;
i;
故选:B.
【点评】本题考查复数的代数形式的混合运算,考查计算能力.
2.(5分)已知全集U=R,集合M={x||x﹣2|≤1},则∁UM=( )
A.(1,3) B.[1,3]
C.(﹣∞,1)∪(3,+∞) D.(﹣∞,1]∪[3,+∞)
【考点】1F:补集及其运算.菁优网版权所有
【分析】先求出M,再利用补集的定义求出结论.
【解答】解:因为全集U=R,集合M={x||x﹣2|≤1}={x|﹣1≤x﹣2≤1}={x|1≤x≤3},
∴∁UM=(﹣∞,1)∪(3,+∞).
故选:C.
【点评】本题考查集合的基本运算,是对基本知识的考查.
3.(5分)设Sn是等差数列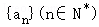 的前n项和,且a_1=1,_S_5=25,则_a_2=( )
的前n项和,且a_1=1,_S_5=25,则_a_2=( )
A.4 B.3 C.2 D.5
【考点】85:等差数列的前n项和.菁优网版权所有
【分析】设等差数列{_a__n}的公差为d,由已知列式求得d,再由通项公式求a_2.
【解答】解:设等差数列{_a__n}的公差为d,
由a_1=1,_S_5=25,得25=5×1+ ,即_d=2.
,即_d=2.
∴a_2=_a_1+_d=3.
故选:B.
【点评】本题考查等差数列的通项公式与前n项和,是基础的计算题.
4.(5分)保护生态环境是每个公民应尽的职责!某校随机抽取100名同学进行“垃圾分类”的问卷测试,测试结果发现这100名同学的得分都在[50,100]内,按得分分成5组:[50,60),[60,70),[70,80),[80,90),[90,100],得到如图所示的频率分布直方图,则估计这100名同学的得分的众数为( )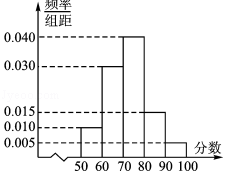
A.70 B.72.5 C.80 D.75
【考点】B8:频率分布直方图.菁优网版权所有
【分析】利用众数的估计值为频率最大区间的区间中点值即可算出结果.
【解答】解:由频率分布直方图可知,这5组中[70,80)组的频率最大,所以众数为这一组的区间中点值,即众数是75,
故选:D.
【点评】本题主要考查了众数的估计值,是基础题.
5.(5分)执行如图所示的程序框图,若输入k,n的值均是0,则输出T的值为( )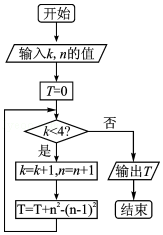
A.9 B.16 C.25 D.36
【考点】EF:程序框图.菁优网版权所有
【分析】由已知中的程序语句可知:该程序的功能是利用循环结构计算并输出变量T的值,模拟程序的运行过程,分析循环中各变量值的变化情况,可得答案.
【解答】解:模拟程序的运行,可得
k=0,n=0,T=0
满足条件k<4,执行循环体,k=1,n=1,T=0+12﹣02=1
满足条件k<4,执行循环体,k=2,n=2,T=1+22﹣12=4
满足条件k<4,执行循环体,k=3,n=3,T=4+32﹣22=9
满足条件k<4,执行循环体,k=4,n=4,T=9+42﹣32=16
此时,不满足条件k<4,退出循环,输出T的值为16.
故选:B.
【点评】本题考查了程序框图的应用问题,解题时应模拟程序框图的运行过程,以便得出正确的结论,是基础题.
6.(5分)用数字1,2,3组成无重复数字的三位数,那么所有的三位数中是奇数的概率为( )
A.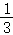 B.
B.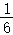 C.
C. D.
D.
【考点】CB:古典概型及其概率计算公式.菁优网版权所有
【分析】基本事件总数n= ,其中奇数的个数m=
,其中奇数的个数m= =4,由此能求出所有的三位数中是奇数的概率.
=4,由此能求出所有的三位数中是奇数的概率.
【解答】解:用数字1,2,3组成无重复数字的三位数,
基本事件总数n= ,
,
其中奇数的个数m= =4,
=4,
∴所有的三位数中是奇数的概率为p=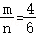 =
= .
.
故选:D.
【点评】本题考查概率的求法,考查古典概型、排列组合等基础知识,考查运算求解能力,是基础题.
7.(5分)在矩形ABCD中,AB=3,AD=4,平面上一点P满足PA=1,PC=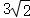 ,则
,则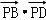 =( )
=( )
A.﹣3 B.3 C.0 D.1
【考点】9O:平面向量数量积的性质及其运算.菁优网版权所有
【分析】画出图形,建立直角坐标系,设出坐标,然后利用向量的数量积求解即可.
【解答】解:画出图形,并建立平面直角坐标系如图:
由题意可知A(0,0),B(0,3),C(4,3),D(4,0),
平面上一点P满足PA=1,PC=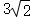 ,PA=1,PC=
,PA=1,PC=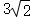 ,
,
可知P(x,y)的坐标满足 ,解得
,解得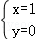 或
或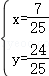 ,
,
当P(1,0),
此时 =(﹣1,3)•(3,0)=﹣3,
=(﹣1,3)•(3,0)=﹣3,
当P( ,
,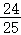 )时,
)时, =(﹣
=(﹣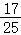 ,
,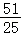 )•(
)•(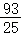 ,﹣
,﹣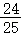 )=﹣
)=﹣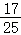 ×
×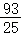 ﹣
﹣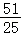 ×
×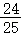 =﹣3.
=﹣3.
故选:A.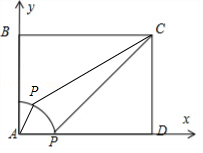
【点评】本题考查平面向量的数量积的运算,考查转化思想以及计算能力,是基础题,
8.(5分)已知函数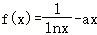 在(1,+∞)上有极值,则实数a的取值范围为( )
在(1,+∞)上有极值,则实数a的取值范围为( )
A.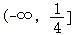 B.
B.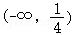 C.
C. D.
D.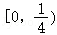
【考点】6D:利用导数研究函数的极值.菁优网版权所有
【分析】求导可得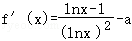 ,设
,设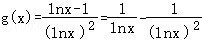 ,依题意,f′(x)=g(x)﹣a在(1,+∞)上有变号零点,令
,依题意,f′(x)=g(x)﹣a在(1,+∞)上有变号零点,令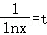 ,则
,则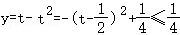 ,由此即可求得a的取值范围.
,由此即可求得a的取值范围.
【解答】解: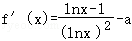 ,设
,设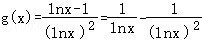 ,
,
∵函数f(x)在区间(1,+∞)上有极值,
∴f′(x)=g(x)﹣a在(1,+∞)上有变号零点,
令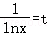 ,由x>1可得lnx>0,即t>0,
,由x>1可得lnx>0,即t>0,
得到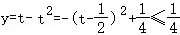 ,
,
∴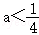 .
.
故选:B.
【点评】本题考查根据函数的极值求参数的取值范围,考查学生的转化能力和运算能力,属于中档题.
9.(5分)在三棱锥P﹣ABC中,PA⊥平面ABC,PA=2,AB=4,AC=3,∠BAC= ,则三棱锥P﹣ABC的外接球的半径R=( )
,则三棱锥P﹣ABC的外接球的半径R=( )
A.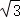 B.
B.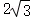 C.
C.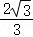 D.
D.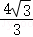
【考点】LR:球内接多面体.菁优网版权所有
【分析】由已知利用余弦定理求出BC,可得△ABC外接圆的半径,再由勾股定理可求该三棱锥的外接球的半径.
【解答】解:∵AC=3,AB=4,∠BAC= ,
,
∴由余弦定理可得BC=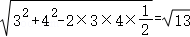 ,
,
∴△ABC外接圆的半径r=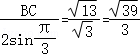 ,
,
设球心到平面ABC的距离为d,则d= PA=1.
PA=1.
由勾股定理可得R=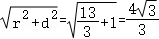 ,
,
故选:D.
【点评】本题考查多面体外接球半径的求法,考查空间想象能力与思维能力,考查计算能力,是中档题.
10.(5分)设A,B为双曲线Γ: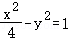 的左,右顶点,F为双曲线Γ右焦点,以原点O为圆心,|OF|为半径的圆与双曲线Γ的一条渐近线的一个交点为M,连接AM,BM,则tan∠AMB=( )
的左,右顶点,F为双曲线Γ右焦点,以原点O为圆心,|OF|为半径的圆与双曲线Γ的一条渐近线的一个交点为M,连接AM,BM,则tan∠AMB=( )
A.4 B. C.2 D.
C.2 D.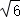
【考点】KC:双曲线的性质.菁优网版权所有
【分析】画出图形,利用双曲线的性质,求出M坐标,然后转化求解tan∠AMB即可.
【解答】解:由题意可知双曲线的图形如图:设A,B为双曲线Γ: 的左,右顶点,F为双曲线Γ右焦点,以原点O为圆心,|OF|为半径的圆与双曲线Γ的一条渐近线的一个交点为M,连接AM,BM,
的左,右顶点,F为双曲线Γ右焦点,以原点O为圆心,|OF|为半径的圆与双曲线Γ的一条渐近线的一个交点为M,连接AM,BM,
OM=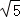 ,OA=2,tan∠MOA=
,OA=2,tan∠MOA=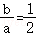 ,
,
所以AM=1,M(2,1),AB=4,
所以在直角三角形ABM中,tan∠AMB= =
=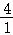 =4.
=4.
故选:A.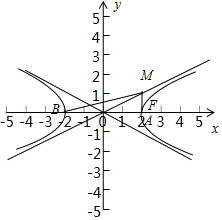
【点评】本题考查双曲线的简单性质的应用,考查转化思想以及计算能力,是中档题.
11.(5分)已知数列{a__n}满足an+1=an+a__n﹣1(n≥2),又{a__n}的前项和为Sn,若S_6=52,则_a_5=( )
A.13 B.15 C.17 D.31
【考点】8E:数列的求和;8H:数列递推式.菁优网版权所有
【分析】首先根据题意,将_S_6转化为_a_5的关系式,然后求出_a_5即可.
【解答】解:∵_an+1=an+a__n﹣1(n≥2),
∴S_6=_a_1+_a_2+_a_3+_a_4+_a_5+_a_6=_a_3+_a_3+_a_4+_a_5+_a_5+_a_4
=2(_a_3+_a_4)+2_a_5=4_a_5=52,
∴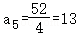 .
.
故选:_A.
【点评】本题考查了数列的递推公式,数列的求和问题,属基础题.
12.(5分)已知抛物线C_1: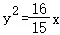 和圆_C_2:(_x﹣6)2+(y﹣1)2=1,过圆C_2上一点_P作圆的切线MN交抛物线C_1于_M,N两点,若点P为MN的中点,则切线MN的斜率k>1时的直线方程为( )
和圆_C_2:(_x﹣6)2+(y﹣1)2=1,过圆C_2上一点_P作圆的切线MN交抛物线C_1于_M,N两点,若点P为MN的中点,则切线MN的斜率k>1时的直线方程为( )
A.4x﹣3y﹣22=0 B.4x﹣3y﹣16=0
C.2x﹣y﹣11+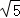 =0 D.4x﹣3y﹣26=0
=0 D.4x﹣3y﹣26=0
【考点】KJ:圆与圆锥曲线的综合.菁优网版权所有
【分析】设P(x_0,_y_0),_M(x_1,_y_1),_N(x_2,_y_2),代入抛物线的方程,由作差法可得直线_MN的斜率,结合中点坐标公式和P的坐标满足圆的方程,以及两直线垂直的条件:斜率之积为﹣1,消去x_0,_y_0,可得_k的方程,结合选项的直线的斜率,代入求得P的坐标,检验是否满足圆的方程,即可得到所求直线的方程.
【解答】解:设P(x_0,_y_0),_M(x_1,_y_1),_N(x_2,_y_2),
可得_y_12= _x_1,_y_22=
_x_1,_y_22= _x_2,
_x_2,
两式相减可得(_y_1﹣_y_2)(_y_1+_y_2)= (_x_1﹣_x_2),
(_x_1﹣_x_2),
可得_k=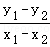 =
=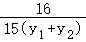 ,
,
若点P为MN的中点,可得2y_0=_y_1+_y_2,
即有_y_0=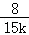 ,①
,①
又(_x_0﹣6)2+(_y_0﹣1)2=1,②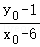 =﹣
=﹣ ,_k>1,③
,_k>1,③
由①②③消去x_0,_y_0,可得(1+_k_2)(1﹣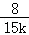 )2=1,
)2=1,
由选项可得,当_k=2时,y_0=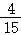 ,_x_0=
,_x_0= ,
,
代入②,不成立;
当_k=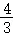 时,y_0=
时,y_0=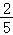 ,_x_0=
,_x_0=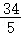 ,
,
代入②,成立.
此时直线_MN的方程为y﹣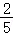 =
= (x﹣
(x﹣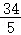 ),
),
即为4x﹣3y﹣26=0.
故选:D.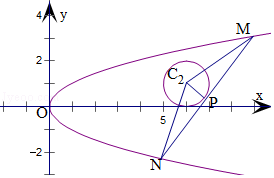
【点评】本题考查抛物线和圆的方程的运用,考查直线和圆的位置关系、直线和抛物线的位置关系,主要考查方程思想和运算能力,属于中档题.
二、填空题:本题共4小题,每小题5分,共20分.
13.(5分)函数y=(2x_2+1)_ex在点(0,1)处的切线方程为 x﹣y+1=0 .
【考点】6H:利用导数研究曲线上某点切线方程.菁优网版权所有
【分析】求出原函数的导函数,得到函数在x=0处的导数,再由直线方程的点斜式得答案.
【解答】解:由y=(2x_2+1)_ex,得y′=4xe__x+(2x_2+1)_ex=(2x_2+4_x+1)ex.
∴y′|x=0=1,
则函数y=(2x_2+1)_ex在点(0,1)处的切线方程为y=x+1,即x﹣y+1=0.
故答案为:x﹣y+1=0.
【点评】本题考查利用导数研究故曲线上某点处的切线方程,关键是熟记导数的运算法则,是基础题.
14.(5分)若实数x、y满足约束条件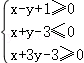 ,则z=2x﹣y的最大值为 6 .
,则z=2x﹣y的最大值为 6 .
【考点】7C:简单线性规划.菁优网版权所有
【分析】由约束条件作出可行域,化目标函数为直线方程的斜截式,数形结合得到最优解,把最优解的坐标代入目标函数得答案.
【解答】解:由实数x、y满足约束条件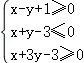 ,作出可行域:
,作出可行域:
联立 ,解得A(3,0),
,解得A(3,0),
化z=2x﹣y为y=2x﹣z,由图可知,当直线y=2x﹣z过A时,直线在y轴上的截距最小,z有最大值为:6.
故答案为:6.
【点评】本题考查简单的线性规划,考查了数形结合的解题思想方法,是中档题.
15.(5分)一条河的两岸平行,河的宽度d=4km,一艘船从岸边A处出发到河的正对岸,已知船的速度|v_1|=10_km/h,水流速度|v_2|=2_km/h,那么行驶航程最短时,所用时间是 0.41 (h).(附: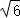 ≈2.449,精确到0.01h).
≈2.449,精确到0.01h).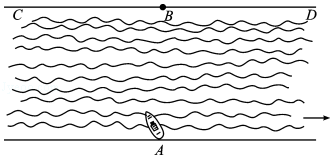
【考点】HU:解三角形.菁优网版权所有
【分析】利用河的宽度为4km,结合船的静水速度船的速度|v_1|=10_km/h,水流速度|v_2|=2_km/h,利用数列的减法运算求出和速度,即可求解行驶航程最短时所用时间.
【解答】解:如图:行驶航程最短时,就是船垂直到达对岸,
∴和速度为:v= (km/h)≈9.796km/h.
(km/h)≈9.796km/h.
∴行驶航程最短时,所用时间是: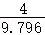 ≈0.41h.
≈0.41h.
故答案为:0.41.
【点评】本题考查三角形的解法,实际问题的处理方法,是基本知识的考查.
16.(5分)已知函数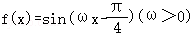 ,满足不等式
,满足不等式 在R上恒成立,在
在R上恒成立,在 上恰好只有一个极值点,则实数ω=
上恰好只有一个极值点,则实数ω= 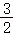 .
.
【考点】HW:三角函数的最值.菁优网版权所有
【分析】因为不等式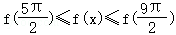 在R上恒成立,所以
在R上恒成立,所以 ,可解得
,可解得 ①,又函数f(x)在
①,又函数f(x)在 上恰好只有一个极值点,所以
上恰好只有一个极值点,所以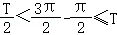 ,解得1<ω≤2②,结合①②可得,当k_1=2,_k_2=3时,
,解得1<ω≤2②,结合①②可得,当k_1=2,_k_2=3时,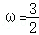 .
.
【解答】解:∵不等式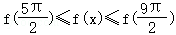 在R上恒成立,∴
在R上恒成立,∴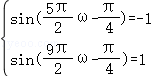 ,
,
∴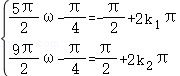 ,即
,即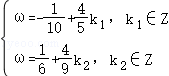 ①,
①,
∵函数_f(x)在 上恰好只有一个极值点,
上恰好只有一个极值点,
∴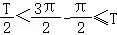 ,即
,即 ,
,
∴1<ω≤2②,
结合①②可得,当k_1=2,_k_2=3时,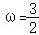 .
.
故答案为: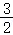 .
.
【点评】本题考查正弦函数的图象与性质,考查学生的逻辑推理能力和运算能力,属于中档题.
三、解答题:共70分.解答应写出文字说明、证明过程或演算步骤.第17~21题为必考题,每个试题考生都必须作答.第22、23题为选考题,考生根据要求作答.(一)必考题:共60分
17.(12分)△_ABC的内角A,B,C的对边分别为a、b、c,若a+c=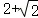 ,cosA=
,cosA= ,sinC=
,sinC=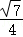 .
.
(1)求sinB;
(2)求△ABC的面积.
【考点】HP:正弦定理.菁优网版权所有
【分析】(1)由已知结合同角平方关系及和差角公式即可求解;
(2)由已知结合正弦定理可求b,进而可求a,然后结合三角形的面积公式即可求解.
【解答】解:(1)在△ABC中,由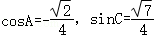 ,知:
,知: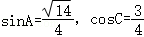 .
.
所以sinB=sin(A+C)=sinA_cos_C+sinC_cos_A
=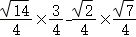 =
= ;
;
(2)由正弦定理可知: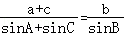 ,即
,即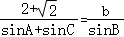 ,因此b=1.
,因此b=1.
由b=1,及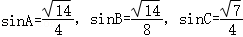 ,可知a=2.
,可知a=2.
所以△ABC的面积为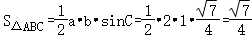 .
.
【点评】本题主要考查了同角平方关系及和差角公式,正弦定理的应用,属于中档试题.
18.(12分)如图,在四棱锥P﹣ABCD中,PA⊥平面ABCD,在四边形ABCD中,∠ABC=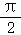 ,AB=4,BC=3,CD=
,AB=4,BC=3,CD= ,AD=2
,AD=2 ,PA=4.
,PA=4.
(1)证明:CD⊥平面PAD;
(2)求二面角B﹣PC﹣D的余弦值.
【考点】LW:直线与平面垂直;MJ:二面角的平面角及求法.菁优网版权所有
【分析】(1)依题意,可得AD⊥CD,由线面垂直的性质可得PA⊥CD,进而得证;
(2)利用等体积法求出B点到直线PC的距离,进而求得二面角B﹣PC﹣D的余弦值.
【解答】解:(1)在平面ABCD中,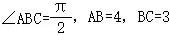 ,
,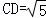 ,
,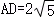 ,
,
∴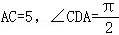 ,即AD⊥CD,
,即AD⊥CD,
又PA⊥平面ABCD,则PA⊥CD,
又AD∩PA=A,
∴CD⊥平面PAD.……………….(6分)
(2)在平面ABCD中,过A 作BC的平行线交CD的延长线于M,
∵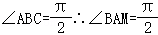 .
.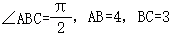 ,
,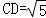 ,
, ,
,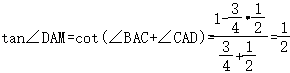 ,
,
又 ,则
,则 ,
,
由VP﹣BCM=VB﹣PCM可知:S△BCM•PA=S△PCM•hB﹣PCM
即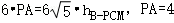 ,则
,则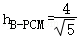 ,
,
在△BPC中,B点到直线PC的距离
设二面角B﹣PC﹣D的平面角为θ,则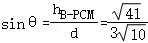
所以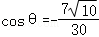 .……………….(12分)
.……………….(12分)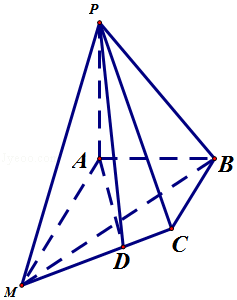
【点评】本题考查线面垂直的判定以及二面角的求解,考查推理论证能力及运算求解能力,属于中档题.
19.(12分)已知椭圆Γ: 的左,右焦点分别为F_1(
的左,右焦点分别为F_1( ,0),_F_2(
,0),_F_2(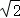 ,0),椭圆的左,右顶点分别为_A,B,已知椭圆Γ上一异于A,B的点P,PA,PB的斜率分别为k_1,_k_2,满足
,0),椭圆的左,右顶点分别为_A,B,已知椭圆Γ上一异于A,B的点P,PA,PB的斜率分别为k_1,_k_2,满足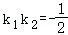 .
.
(1)求椭圆Γ的标准方程;
(2)若过椭圆Γ左顶点_A作两条互相垂直的直线AM和AN,分别交椭圆Γ于M,N两点,问x轴上是否存在一定点Q,使得∠MQA=∠NQA成立,若存在,则求出该定点Q,否则说明理由.
【考点】K3:椭圆的标准方程;KL:直线与椭圆的综合.菁优网版权所有
【分析】(1)设P(x_0,_y_0),利用直线的斜率关系,结合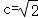 ,求解_a,b,然后求解椭圆方程.
,求解_a,b,然后求解椭圆方程.
(2)设直线AM和AN的方程分别为y=k(x+2)和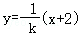 ,
,
设M(xM,yM),N(xN,yN),联立直线方程与椭圆方程,求出M、N的坐标,设x轴上存在一定点Q(t,0),使得∠MQA=∠NQA成立,kQM+k__QN=0,转化求解即可.
【解答】解:(1)设P(x_0,_y_0),则_y_02=_b_2(1﹣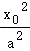 ),
),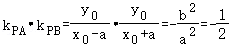 ,
,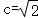 ,
,
则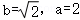 ,
,
∴椭圆Γ的标准方程为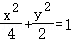 .
.
(2)由(1)知_A(﹣2,0),且直线AM和AN的斜率存在,
设直线AM和AN的方程分别为y=k(x+2)和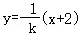 ,
,
设M(xM,yM),N(xN,yN),
联立 ,
,
∵直线AM和椭圆Γ交于A,M两点
∴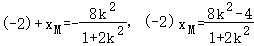 ,
,
∴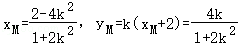 ,
,
∴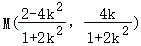 ,
,
同理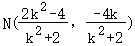 ,
,
设x轴上存在一定点Q(t,0),使得∠MQA=∠NQA成立,kQM+k__QN=0,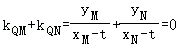 ,
,
则yM•xN+y__N•xM=(yM+y__N)•t, ,
,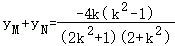 ,
,
可得t=﹣6,
因此x轴上存在一定点Q(﹣6,0),使得∠MQA=∠NQA成立.
【点评】本题考查椭圆方程的求法,直线与椭圆的位置关系的应用,考查转化思想以及计算能力,是难题.
20.(12分)由甲乙两位同学组成一个小组参加年级组织的篮球投篮比赛,共进行两轮投篮,每轮甲乙各自独立投篮一次,并且相互不受影响,每次投中得2分,没投中得0分.已知甲同学每次投中的概率为 ,乙同学每次投中的概率为
,乙同学每次投中的概率为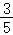 .
.
(1)求第一轮投篮时,甲乙两位同学中至少有一人投中的概率;
(2)甲乙两位同学在两轮投篮中,记总得分为随机变量ξ,求ξ的分布列和期望.
【考点】CG:离散型随机变量及其分布列;CH:离散型随机变量的期望与方差.菁优网版权所有
【分析】(1)利用相互独立数据的概率的乘法,求解概率,结合对立事件的概率求解即可.
(2)求出P(ξ=X+Y),然后求解期望即可.
【解答】解:(1)第一轮投篮时,甲乙两位同学中都没有投中的概率为
甲乙两位同学中至少有一人投中的概率为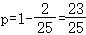 .
.
(2)对甲: ,
,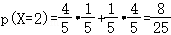 ,
,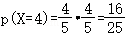
对乙: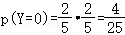 ,
,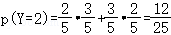 ,
,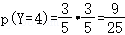 ,
,
| Y=0 | Y=2 | Y=4 | P(X=j) | |
|---|---|---|---|---|
| X=0 | 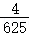 |
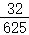 |
 |
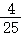 |
| X=2 | 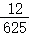 |
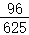 |
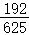 |
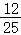 |
| X=4 | 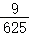 |
 |
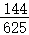 |
 |
| P(Y=i) | 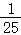 |
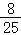 |
 |
记p(ξ=X+Y):则有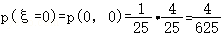 ,
,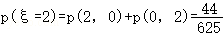 ,
, ,
, ,
,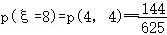 ,
,
所以,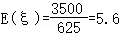 .
.
【点评】本题考查离散型随机变量的的概率的求法,期望的求法,考查分析问题解决问题的能力.
21.(12分)(1)已知实数a>0,若关于x的不等式sinx﹣x_cos_ax≥0在0≤x≤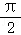 上恒成立,求实数a的取值范围;
上恒成立,求实数a的取值范围;
(2)若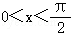 ,求证:
,求证: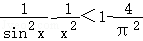 .
.
【考点】6E:利用导数研究函数的最值;R6:不等式的证明.菁优网版权所有
【分析】(1)设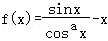 ,问题可以转化为f(x)≥0,在0≤x≤
,问题可以转化为f(x)≥0,在0≤x≤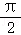 上恒成立,先求f(x),再求f″(x)=sinx•cos﹣ax[(3a﹣1)+a(a+1)tan2x],分两种情况:①在
上恒成立,先求f(x),再求f″(x)=sinx•cos﹣ax[(3a﹣1)+a(a+1)tan2x],分两种情况:①在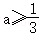 时,②在
时,②在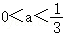 时,分析f″(x)的正负,f′(x)的增减,得f(x)的增减,进而得f(x)的函数值取值范围.是否符合题意,进而得出结论.
时,分析f″(x)的正负,f′(x)的增减,得f(x)的增减,进而得f(x)的函数值取值范围.是否符合题意,进而得出结论.
(2)设 ,对g(x)求函数导数得:g′(x)=2(
,对g(x)求函数导数得:g′(x)=2(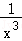 ﹣
﹣ ),由(1)可知当a=
),由(1)可知当a=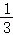 时,sinx﹣x_cos
时,sinx﹣x_cos _x≥0在0≤x≤
_x≥0在0≤x≤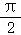 上恒成立,得
上恒成立,得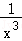 ≥
≥ 在0≤x≤
在0≤x≤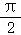 上恒成立,g′(x)≥0,g(x)在
上恒成立,g′(x)≥0,g(x)在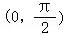 上为增函数,则g(x)≤g(
上为增函数,则g(x)≤g(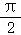 ),进而得出结论.
),进而得出结论.
【解答】证明:(1)设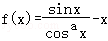 ,
,
则若关于x的不等式sinx﹣x_cos_ax≥0在0≤x≤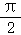 上恒成立,
上恒成立,
可以转化为f(x)≥0,在0≤x≤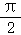 上恒成立,
上恒成立,
对f(x)求函数导数得: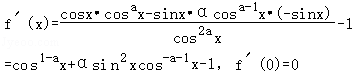
f″(x)=(1﹣a)cos﹣ax•(﹣sinx)+2a_sin_x•cosx_cos﹣_a﹣1x+a_sin2_x•(﹣a﹣1)•cos﹣a﹣2x•(﹣sinx)
=(1﹣a)cos﹣ax•(﹣sinx)+2a_sin_x•cos﹣ax﹣a_sin3_x•(﹣a﹣1)•cos﹣a﹣2x
=sinx•cos﹣ax[(3a﹣1)+a(a+1)tan2x],
①在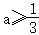 时,有f‘’(x)≥0,则f′(x)在
时,有f‘’(x)≥0,则f′(x)在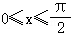 为增函数,而f′(0)=0
为增函数,而f′(0)=0
∴f′(x)≥f′(0)=0,
因此f(x)在 为增函数,
为增函数,
有f(x)≥f(0)=0
从而f(x)≥0.
所以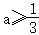 符合要求.
符合要求.
②在 时,
时,
由f‘’(x)=0可知: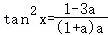 ,
,
令 ,
,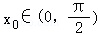 ,
,
因此f′(x)在(0,x_0)为减函数,则_f′(x)≤0,f(x)单调递减,
于是有f(x)≤f(0)=0在(0,x_0)恒成立,从而矛盾,
因此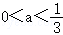 不符合.
不符合.
综合讨论可知: .
.
(2)设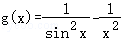 ,
,
对_g(x)求函数导数得: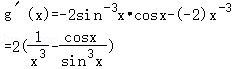
由(1)可知当a=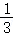 时,sinx﹣x_cos
时,sinx﹣x_cos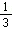 _x≥0在0≤x≤
_x≥0在0≤x≤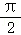 上恒成立,
上恒成立,
即sinx≥x_cos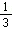 _x在0≤x≤
_x在0≤x≤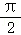 上恒成立,
上恒成立,
所以sin3x≥x_3cos_x在0≤x≤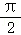 上恒成立,
上恒成立,
即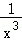 ≥
≥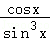 在0≤x≤
在0≤x≤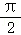 上恒成立,
上恒成立,
可知:g′(x)≥0,
∴g(x)在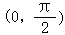 上为增函数,
上为增函数,
则g(x)≤g(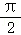 )=1﹣
)=1﹣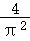 .
.
【点评】本题考查导数的综合应用,三角函数化简,属于中档题.
(二)选考题:共10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程](本小题满分10分)
22.(10分)在平面直角坐标系xOy中,点P是曲线C: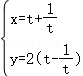 (t为参数)上的动点,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C_2的极坐标方程为:
(t为参数)上的动点,以坐标原点O为极点,x轴的正半轴为极轴建立极坐标系,曲线C_2的极坐标方程为: .
.
(1)求曲线_C_1,_C_2的直角坐标下普通方程;
(2)已知点_Q在曲线C_2上,求|_PQ|的最小值以及取得最小值时P点坐标.
【考点】Q4:简单曲线的极坐标方程;QH:参数方程化成普通方程.菁优网版权所有
【分析】(1)直接利用转换关系,把参数方程极坐标方程和直角坐标方程之间进行转换.
(2)利用点到直线的距离公式的应用和基本不等式的应用求出结果.
【解答】解:(1)由C_1: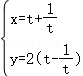 消去参数_t得到
消去参数_t得到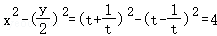 ,
,
所以曲线C_1的直角坐标方程为 .
.
由曲线_C_2:ρsinθ﹣3ρcosθ=2,根据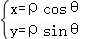 ,整理得直角坐标方程为:_y=3x+2.
,整理得直角坐标方程为:_y=3x+2.
(2)设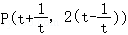 ,
,
则P到直线C_2:_y=3x+2的距离为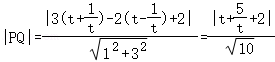 ,
,
当t>0时,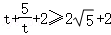 ,当t<0时,
,当t<0时,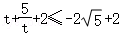 ,
,
所以当t<0,且t=﹣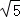 时,整理得
时,整理得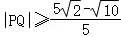 ,
,
此时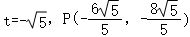 .
.
【点评】本题考查的知识要点:参数方程极坐标方程和直角坐标方程之间的转换,直线与圆的位置关系的应用,基本不等式的应用,点到直线的距离公式的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.
[选修4-5:不等式选讲](本小题满分0分)
23.已知f(x)=|ax+1|,a∈R.
(1)若关于x的不等式f(x)≤3的解集为{x|﹣2≤x≤1},求实数a的值;
(2)若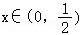 时,不等式f(x)≤2﹣|2x﹣1|恒成立.求实数a的取值范围.
时,不等式f(x)≤2﹣|2x﹣1|恒成立.求实数a的取值范围.
【考点】6P:不等式恒成立的问题;R5:绝对值不等式的解法.菁优网版权所有
【分析】(1)由绝对值不等式的解法和已知解集,讨论a≤0,a>0,结合方程解法,可得a的值;
(2)由题意可得|ax+1|+|2x﹣1|≤2在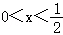 恒成立,所以|ax+1|≤2x+1,转化为﹣2x﹣2≤ax≤2x,再由参数分离和恒成立思想,可得a的范围.
恒成立,所以|ax+1|≤2x+1,转化为﹣2x﹣2≤ax≤2x,再由参数分离和恒成立思想,可得a的范围.
【解答】解:(1)由|ax+1|≤3得﹣4≤ax≤2,又f(x)≤3的解集为{x|﹣2≤x≤1},
所以当a=0时,不合题意;
当a<0时, ≤x≤﹣
≤x≤﹣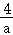 ,有
,有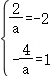 ,则a∈∅,不合题意;
,则a∈∅,不合题意;
当a>0时,﹣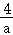 ≤x≤
≤x≤ ,
,
即有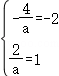 ,
,
解得a=2;
(2)因为|ax+1|+|2x﹣1|≤2在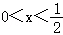 恒成立,
恒成立,
所以|ax+1|≤2x+1,即﹣(2x+1)≤ax+1≤2x+1,
即﹣2x﹣2≤ax≤2x,
所以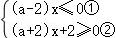 ,
,
由①,得a≤2;
由②,得 在
在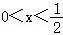 恒成立,所以
恒成立,所以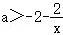 .
.
因为 ,所以a≥﹣6.
,所以a≥﹣6.
综上可知,实数a的取值范围为﹣6≤a≤2.
【点评】本题考查绝对值不等式的解法和不等式恒成立问题解法,考查分类讨论思想和转化思想,考查化简运算能力和推理能力,属于中档题.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/6/25 20:45:43;用户:17859775485;邮箱:17859775485;学号:21682042

