2020年广东省梅州市高考数学二模试卷(理科)
一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的.
1.(5分)复数z=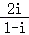 ,则其共轭复数
,则其共轭复数 =( )
=( )
A.﹣1﹣i B.﹣1+i C.1﹣i D.1+i
2.(5分)已知集合M={y|y=x_2﹣1,_x∈R},N={x|y=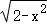 },则M∩N=( )
},则M∩N=( )
A.∅ B.[﹣1,+∞) C.[﹣1, ] D.[
] D.[ ,+∞)
,+∞)
3.(5分)在△ABC中,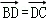 ,E是AD的中点,则
,E是AD的中点,则 =( )
=( )
A.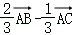 B.
B. C.
C. D.
D.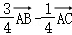
4.(5分)以下四个命题:
①若p∧q为假命题,则p,q均为假命题;
②对于命题p:∃x_0∈R,_x_02+_x_0+1<0,则¬_p为:∀x∉R,x_2+_x+1≥0;
③“a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件;
④f(x)=sin(ωx+φ)为偶函数的充要条件是φ=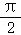 .
.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
5.(5分)2021年起,我省将实行“3+1+2”高考模式,某中学为了解本校学生的选考情况,随机调查了100位学生,其中选考化学或生物的学生共有70位,选考化学的学生共有40位,选考化学且选考生物的学生共有20位.若该校共有1500位学生,则该校选考生物的学生人数的估计值为( )
A.300 B.450 C.600 D.750
6.(5分)(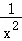 +4x_2+4)3展开式的常数项为( )
+4x_2+4)3展开式的常数项为( )
A.120 B.160 C.200 D.240
7.(5分)已知在各项均不为零的等差数列{_a__n}中,2a_3﹣_a_72+2_a_11=0,数列{_b__n}是等比数列,且b_7=_a_7,则_b_6•_b_8等于( )
A.2 B.4 C.8 D.16
8.(5分)某几何体的三视图如图所示,已知其主视图的周长为8,则该几何体侧面积的最大值为( )
A.2π B.4π C.16π D.不存在
9.(5分)若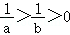 ,有下列四个不等式:
,有下列四个不等式:
①_a_3<_b_3;
②log_a+23>logb+13;
③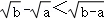 ;
;
④a_3+_b_3>2_ab_2.
则下列组合中全部正确的为( )
A.①② B.①③ C.①④ D.②③
10.(5分)已知直线_l_1:2_x﹣y+3=0和直线l_2:_x=﹣1,抛物线y_2=4_x上的点P到直线l_1和直线_l_2的距离之和的最小值是( )
A.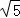 B.2 C.
B.2 C. D.
D.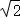
11.(5分)祖暅是南北朝时代的伟大数学家,五世纪末提出几何体体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等,现在有四个几何体:图①是从圆柱中挖去一个圆锥所得的几何体,图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )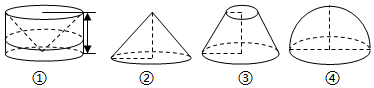
A.①② B.①③ C.②④ D.①④
12.(5分)在直角坐标系_xOy中,如果相异两点A(a,b),B(﹣a,﹣b)都在函数y=f(x)的图象上,那么称A,B为函数f(x)的一对关于原点成中心对称的点对(A,B与B,A为同一对).函数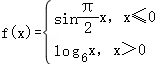 图象上关于原点成中心对称的点对有( )
图象上关于原点成中心对称的点对有( )
A.1对 B.2对 C.3对 D.4对
二、填空题:本大题共4个小题,每小题5分,共20分
13.(5分)已知数列{a__n}的前n项和为Sn,a_1=1,_Sn=2a__n+1,则Sn= .
14.(5分)曲线f(x)=tanx在点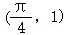 处的切线方程为 .
处的切线方程为 .
15.(5分)某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系y=ekx+b(e为自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是384小时,在22℃的保鲜时间是24小时,则该食品在33℃的保鲜时间是 .
16.(5分)已知双曲线C: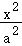 ﹣
﹣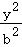 =1(a>0,b>0)的左、右焦点分别为F_1,_F_2,_O为坐标原点,P是双曲线在第一象限上的点,直线PO,PF_2分别交双曲线_C左、右支于另一点M,N,若|PF_1|=2|_PF_2|,且∠_MF_2_N=60°,则双曲线C的离心率为 .
=1(a>0,b>0)的左、右焦点分别为F_1,_F_2,_O为坐标原点,P是双曲线在第一象限上的点,直线PO,PF_2分别交双曲线_C左、右支于另一点M,N,若|PF_1|=2|_PF_2|,且∠_MF_2_N=60°,则双曲线C的离心率为 .
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个考生都必须作答;第22-23题为选考题,考生根据要求作答.(一)必考题:60分
17.(12分)已知a,b,c分别为锐角△ABC三个内角A,B,C的对边,满足sin2A﹣sin2B﹣sin2C+sinB_sin_C=0.
(1)求A;
(2)若b=2,求△ABC面积的取值范围.
18.(12分)如图△PAD中,∠PDA=90°,DP=DA=2,B、C分别是PA、PD的中点,将△PBC沿BC折起,连结PA、PD,得到多面体PABCD.
(1)证明:在多面体PABCD中,BC⊥PD;
(2)在多面体PABCD中,当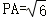 时,求二面角B﹣PA﹣D的余弦值.
时,求二面角B﹣PA﹣D的余弦值.
19.(12分)某市《城市总体规划(2016﹣2035年)》提出到2035年实现“15分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身4个方面构建“15分钟社区生活圈”指标体系,并依据“15分钟社区生活圈”指数高低将小区划分为:优质小区(指数为0.6~1)、良好小区(指数为0.4~0.6)、中等小区(指数为0.2~0.4)以及待改进小区(指数为0~0.2)4个等级.下面是三个小区4个方面指标的调查数据:
小区 指标值 权重 |
A小区 |
B小区 |
C小区 |
|---|---|---|---|
| 教育与文化(0.20) | 0.7 | 0.9 | 0.1 |
| 医疗与养老(0.20) | 0.7 | 0.6 | 0.3 |
| 交通与购物(0.32) | 0.5 | 0.7 | 0.2 |
| 休闲与健身(0.28) | 0.5 | 0.6 | 0.1 |
注:每个小区“15分钟社区生活圈”指数T=_w_1_T_1+_w_2_T_2+_w_3_T_3+_w_4_T_4,其中_w_1,_w_2,_w_3,_w_4为该小区四个方面的权重,_T_1,_T_2,_T_3,_T_4为该小区四个方面的指标值(小区每一个方面的指标值为0~1之间的一个数值).
现有100个小区的“15分钟社区生活圈”指数数据,整理得到如下频数分布表:
| 分组 | [0,0.2) | [0.2,0.4) | [0.4,0.6) | [0.6,0.8) | [0.8,1] |
|---|---|---|---|---|---|
| 频数 | 10 | 20 | 30 | 30 | 10 |
(Ⅰ)分别判断A,B,C三个小区是否是优质小区,并说明理由;
(Ⅱ)对这100个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取10个小区进行调查,若在抽取的10个小区中再随机地选取2个小区做深入调查,记这2个小区中为优质小区的个数为ξ,求ξ的分布列及数学期望.
20.(12分)已知两动圆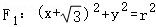 和
和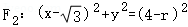 (0<r<4),把它们的公共点的轨迹记为曲线C,若曲线C与y轴的正半轴的交点为M,且曲线C上的相异两点A、B满足:
(0<r<4),把它们的公共点的轨迹记为曲线C,若曲线C与y轴的正半轴的交点为M,且曲线C上的相异两点A、B满足: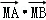 =0.
=0.
(1)求曲线C的方程;
(2)证明直线AB恒经过一定点,并求此定点的坐标;
(3)求△ABM面积S的最大值.
21.(12分)已知函数f(x)=2lnx﹣ax_2+ .
.
(1)当0<_a<1时,求证: ;
;
(2)当f(x)有三个零点时,求a的取值范围.
选考题:10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程](10分)
22.(10分)以直角坐标系的原点为极点,x轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位,已知直线的参数方程为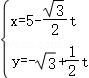 (t为参数),圆C的极坐标方程为
(t为参数),圆C的极坐标方程为 .
.
(1)求直线和圆C的直角坐标方程;
(2)若点P(x,y)在圆C上,求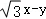 的取值范围.
的取值范围.
[选修4-5:不等式选讲](10分)
23.已知函数f(x)=|2x+3|﹣|x﹣1|.
(1)求不等式f(x)≤3的解集;
(2)若不等式f(x)>2a﹣|3x﹣3|对任意x∈R恒成立,求实数a的取值范围.
2020年广东省梅州市高考数学二模试卷(理科)
参考答案与试题解析
一、选择题:本大题共12个小题,每小题5分,共60分,在每小题给出的四个选项中只有一个是符合题目要求的.
1.(5分)复数z= ,则其共轭复数
,则其共轭复数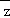 =( )
=( )
A.﹣1﹣i B.﹣1+i C.1﹣i D.1+i
【考点】A5:复数的运算.菁优网版权所有
【分析】化简复数,即可得其共轭复数.
【解答】解:化简可得复数z=
=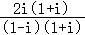 =
= =﹣1+i,
=﹣1+i,
∴复数z的共轭复数为:﹣1﹣i
故选:A.
【点评】本题考查复数的代数形式的乘除运算,涉及共轭复数,属基础题.
2.(5分)已知集合M={y|y=x_2﹣1,_x∈R},N={x|y=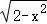 },则M∩N=( )
},则M∩N=( )
A.∅ B.[﹣1,+∞) C.[﹣1,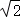 ] D.[
] D.[ ,+∞)
,+∞)
【考点】1E:交集及其运算.菁优网版权所有
【分析】由题意求出集合M与集合N,然后求出M∩N.
【解答】解:集合M={y|y=x_2﹣1,_x∈R}={y|y≥﹣1},
对于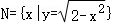 ,2﹣x_2≥0,解得
,2﹣x_2≥0,解得 ,
,
_N={x| },
},
则M∩N=[﹣1,+∞)∩[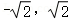 ]=
]=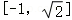 .
.
故选:C.
【点评】本题考查集合的基本运算,函数的值域与函数的定义域的求法,考查集合的交集的求法.
3.(5分)在△ABC中, ,E是AD的中点,则
,E是AD的中点,则 =( )
=( )
A. B.
B.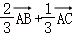 C.
C.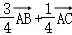 D.
D.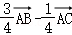
【考点】9H:平面向量的基本定理.菁优网版权所有
【分析】运用向量的加减运算和向量中点的表示,计算可得所求向量.
【解答】解:在△ABC中,AD为BC边上的中线,E为AD的中点, =
=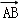 ﹣
﹣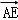 =
=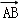 ﹣
﹣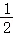
 =
=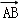 ﹣
﹣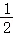 ×
×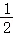 (
(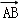 +
+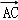 )
)
=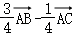 .
.
故选:D.
【点评】本题考查向量的加减运算和向量中点表示,考查运算能力,属于基础题.
4.(5分)以下四个命题:
①若p∧q为假命题,则p,q均为假命题;
②对于命题p:∃x_0∈R,_x_02+_x_0+1<0,则¬_p为:∀x∉R,x_2+_x+1≥0;
③“a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件;
④f(x)=sin(ωx+φ)为偶函数的充要条件是φ= .
.
其中真命题的个数是( )
A.1 B.2 C.3 D.4
【考点】2K:命题的真假判断与应用.菁优网版权所有
【分析】直接利用命题的否定的应用,真值表的应用,三角函数关系式的恒等变换,指数函数的性质的应用求出结果.
【解答】解:①若p∧q为假命题,则命题p和q为一真一假和全部为假,故p,q均为假命题错误;
②对于命题p:∃x_0∈R,_x_02+_x_0+1<0,则¬_p为:∀x∈R,x_2+_x+1≥0;故错误.
③“a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数;当函数f(x)=logax在区间(0,+∞)上为增函数,则a>1.
故③“a=2”是“函数f(x)=logax在区间(0,+∞)上为增函数”的充分不必要条件;正确.
④f(x)=sin(ωx+φ)为偶函数则φ=kπ+ (k∈Z),故错误.
(k∈Z),故错误.
故选:A.
【点评】本题考查的知识要点:命题的否定的应用,真值表的应用,三角函数关系式的恒等变换,指数函数的性质的应用,主要考查学生的运算能力和转换能力及思维能力,属于基础题型.
5.(5分)2021年起,我省将实行“3+1+2”高考模式,某中学为了解本校学生的选考情况,随机调查了100位学生,其中选考化学或生物的学生共有70位,选考化学的学生共有40位,选考化学且选考生物的学生共有20位.若该校共有1500位学生,则该校选考生物的学生人数的估计值为( )
A.300 B.450 C.600 D.750
【考点】C6:等可能事件和等可能事件的概率.菁优网版权所有
【分析】推导出100名学生中考生物的学生有:70﹣40+20=50.该校共有1500位学生,由此能求出该校选考生物的学生人数的估计值.
【解答】解:某中学为了解本校学生的选考情况,随机调查了100位学生,
其中选考化学或生物的学生共有70位,选考化学的学生共有40位,
选考化学且选考生物的学生共有20位.
∴100名学生中考生物的学生有:70﹣40+20=50.
该校共有1500位学生,则该校选考生物的学生人数的估计值为1500× .
.
故选:D.
【点评】本题考查该校选考生物的学生人数的估计值,考查等可能事件概率计算公式等基础知识,考查运算求解能力,是基础题.
6.(5分)(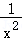 +4x_2+4)3展开式的常数项为( )
+4x_2+4)3展开式的常数项为( )
A.120 B.160 C.200 D.240
【考点】DA:二项式定理.菁优网版权所有
【分析】先对(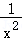 +4_x_2+4)3进行变形,再利用二项式定理中的展开式的通项公式求得结果.
+4_x_2+4)3进行变形,再利用二项式定理中的展开式的通项公式求得结果.
【解答】解:∵(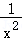 +4_x_2+4)3=[
+4_x_2+4)3=[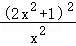 ]3=
]3=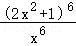 ,(1+2_x_2)6的展开式中的通项公式为_Tr+1=
,(1+2_x_2)6的展开式中的通项公式为_Tr+1=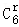 •2rx_2_r,r=0,1,…,6,
•2rx_2_r,r=0,1,…,6,
∴T_4=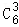 •23_x_6=160_x_6,所以(
•23_x_6=160_x_6,所以( +4_x_2+4)3展开式的常数项为160.
+4_x_2+4)3展开式的常数项为160.
故选:_B.
【点评】本题主要考查对式子的合理变形及二项式定理中的通项公式的应用,属于基础题.
7.(5分)已知在各项均不为零的等差数列{a__n}中,2a_3﹣_a_72+2_a_11=0,数列{_b__n}是等比数列,且b_7=_a_7,则_b_6•_b_8等于( )
A.2 B.4 C.8 D.16
【考点】8M:等差数列与等比数列的综合.菁优网版权所有
【分析】由2_a_3﹣_a_72+2_a_11=0结合性质求得_a_7,再求得_b_7,由等比数列的性质求得_b_6_b_8.
【解答】解:由等差数列的性质:2_a_3﹣_a_72+2_a_11=0得:
∵_a_72=2(_a_3+_a_11)=4_a_7,
∴_a_7=4或_a_7=0,
∴_b_7=4,
∴_b_6_b_8=_b_72=16,
故选:_D.
【点评】本题考查学生灵活运用等差数列的性质及等比数列的性质化简求值,是一道基础题.
8.(5分)某几何体的三视图如图所示,已知其主视图的周长为8,则该几何体侧面积的最大值为( )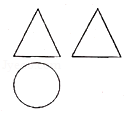
A.2π B.4π C.16π D.不存在
【考点】L!:由三视图求面积、体积.菁优网版权所有
【分析】判断几何体是圆锥,利用主视图的周长为8,推出圆锥的底面半径与高的关系,然后求解几何体侧面积,推出最大值即可.
【解答】解:由题意可知几何体是圆锥,设底面半径为r,r∈(0,2),
高为h,则2r+2 =8,
=8,
即r+ =4,
=4,
所以圆锥的侧面积为:2πr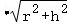 =2πr•(4﹣r)=2π(4r﹣r_2),
=2πr•(4﹣r)=2π(4r﹣r_2),
当且仅当_r=2时,侧面积取得最大值,但是r<2,
所以该几何体侧面积的没有最大值.
故选:D.
【点评】本题考查三视图的应用,判断几何体的形状,以及几何体的侧面积的最值的求法,是中档题.
9.(5分)若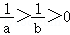 ,有下列四个不等式:
,有下列四个不等式:
①a_3<_b_3;
②log_a+23>logb+13;
③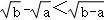 ;
;
④a_3+_b_3>2_ab_2.
则下列组合中全部正确的为( )
A.①② B.①③ C.①④ D.②③
【考点】R3:不等式的基本性质.菁优网版权所有
【分析】根据 ,取_a=2,b=3,则可排除错误选项.
,取_a=2,b=3,则可排除错误选项.
【解答】解:根据 ,取a=2,b=3,
,取a=2,b=3,
则②④不成立,故ACD不正确.
故选:B.
【点评】本题考查了不等式的基本性质,取特殊值是解题的关键,属基础题.
10.(5分)已知直线l_1:2_x﹣y+3=0和直线l_2:_x=﹣1,抛物线y_2=4_x上的点P到直线l_1和直线_l_2的距离之和的最小值是( )
A.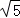 B.2 C.
B.2 C. D.
D.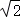
【考点】K8:抛物线的性质;KN:直线与抛物线的综合.菁优网版权所有
【分析】画出图形,过点_P作PN⊥l_2,_PM⊥l_1,垂足分别为_N,M.由于直线l_2是抛物线_y_2=4_x的准线,可得|PN|=|PF|.当且仅当三点M,P,F共线时动点P到直线l_1和_l_2的距离值和取得最小值|_FM|.再利用点到直线的距离公式即可得出.
【解答】解:如图所示,
过点P作PN⊥l_2,_PM⊥l_1,垂足分别为_N,M.
∵直线l_2是抛物线_y_2=4_x的准线,∴|PN|=|PF|.
∴当且仅当三点M,P,F共线时动点P到直线l_1和_l_2的距离值和取得最小值|_FM|.
∴最小值|FM|= =
=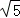 .
.
故选:A.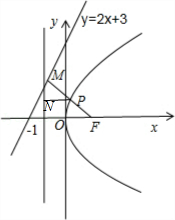
【点评】本题考查了抛物线的性质、点到直线的距离公式,考查了推理能力与计算能力,属于中档题.
11.(5分)祖暅是南北朝时代的伟大数学家,五世纪末提出几何体体积计算原理,即祖暅原理:“幂势既同,则积不容异”.意思是:夹在两个平行平面之间的两个几何体,被平行于这两个平面的任何一个平面所截,如果截面面积都相等,那么这两个几何体的体积一定相等,现在有四个几何体:图①是从圆柱中挖去一个圆锥所得的几何体,图②、图③、图④分别是圆锥、圆台和半球,则满足祖暅原理的两个几何体为( )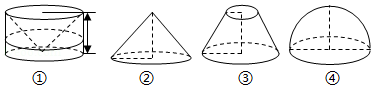
A.①② B.①③ C.②④ D.①④
【考点】LF:棱柱、棱锥、棱台的体积.菁优网版权所有
【分析】利用祖暅原理分析题设中的四个图形,能够得到在①和④中的两个几何体满足祖暅原理.
【解答】解:在①和④中,
夹在两个平行平面之间的这两个几何体,
被平行于这两个平面的任何一个平面所截,
截面面积都相等,
∴①④这两个几何体的体积一定相等.
故选:D.
【点评】本题考查满足祖暅原理的两个几何体的判断,是基础题,解题时要认真审题,注意空间思维能力的培养.
12.(5分)在直角坐标系xOy中,如果相异两点A(a,b),B(﹣a,﹣b)都在函数y=f(x)的图象上,那么称A,B为函数f(x)的一对关于原点成中心对称的点对(A,B与B,A为同一对).函数 图象上关于原点成中心对称的点对有( )
图象上关于原点成中心对称的点对有( )
A.1对 B.2对 C.3对 D.4对
【考点】51:函数的零点;53:函数的零点与方程根的关系.菁优网版权所有
【分析】根据题意,设g(x)的图象与f(x)=sin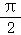 x(x≤0)的图象关于原点对称,结合f(x)的解析式求出g(x)的解析式,分析可得g(x)与f(x)在[0,+∞)上交点的个数,就是函数f(x)的图象上关于原点成中心对称的点对的个数,进而作出函数f(x)=log6x与g(x)=sin
x(x≤0)的图象关于原点对称,结合f(x)的解析式求出g(x)的解析式,分析可得g(x)与f(x)在[0,+∞)上交点的个数,就是函数f(x)的图象上关于原点成中心对称的点对的个数,进而作出函数f(x)=log6x与g(x)=sin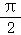 x(x≥0)的图象;结合图象分析可得答案.
x(x≥0)的图象;结合图象分析可得答案.
【解答】解;根据题意,函数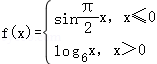 ,当x≤0时,f(x)=sin
,当x≤0时,f(x)=sin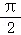 x,
x,
设g(x)的图象与f(x)=sin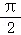 x(x≤0)的图象关于原点对称,
x(x≤0)的图象关于原点对称,
则g(x)=﹣f(﹣x)=﹣sin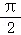 (﹣x)=sin
(﹣x)=sin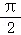 x,
x,
函数g(x)与f(x)在[0,+∞)上交点的个数,就是函数f(x)的图象上关于原点成中心对称的点对的个数,
作出函数f(x)=log6x与g(x)=sin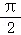 x(x≥0)的图象;
x(x≥0)的图象;
如图所示;
它们有3个公共点,从而f(x)有3对关于原点对称的点;
故选:C.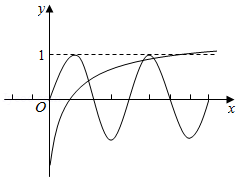
【点评】本题考查函数的零点与方程的关系,注意数形结合思想的应用,属于基础题.
二、填空题:本大题共4个小题,每小题5分,共20分
13.(5分)已知数列{a__n}的前n项和为Sn,a_1=1,_Sn=2a__n+1,则Sn= 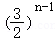 .
.
【考点】8H:数列递推式.菁优网版权所有
【分析】利用数列的递推关系式,推出数列{S__n}是等比数列,然后求解即可.
【解答】解:数列{a__n}的前n项和为Sn,a_1=1,_Sn=2a__n+1,
an+1=Sn+1﹣Sn,可得2S__n+1=3S__n,
所以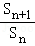 =
=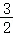 ,数列{S__n}是首项为1,公比为:
,数列{S__n}是首项为1,公比为: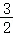 的等比数列,
的等比数列,
则Sn=1•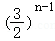 .
.
故答案为: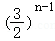 .
.
【点评】本题考查数列的递推关系式的应用,数列求和,考查计算能力.
14.(5分)曲线f(x)=tanx在点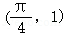 处的切线方程为
处的切线方程为 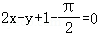 .
.
【考点】6H:利用导数研究曲线上某点切线方程.菁优网版权所有
【分析】先对f(x)求导,然后求出切线的斜率,再求出切线方程即可.
【解答】解:由f(x)=tanx,得f‘(x)=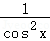 ,
,
∴f(x)=tanx在点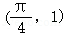 处的切线斜率
处的切线斜率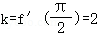 ,
,
∴f(x)=tanx在点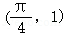 处的切线方程为
处的切线方程为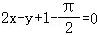 .
.
故答案为: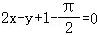 .
.
【点评】本题考查了利用导数研究曲线上某点切线方程,属基础题.
15.(5分)某食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系y=ekx+b(e为自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是384小时,在22℃的保鲜时间是24小时,则该食品在33℃的保鲜时间是 6 .
【考点】5C:根据实际问题选择函数类型.菁优网版权所有
【分析】利用已知条件求出函数的解析式,然后代入求解即可.
【解答】解:食品的保鲜时间y(单位:小时)与储存温度x(单位:℃)满足函数关系y=ekx+b(e为自然对数的底数,k,b为常数),若该食品在0℃的保鲜时间是384小时,在22℃的保鲜时间是24小时,
可得:384=eb,24=e_22_k+b,解得b=ln_384,_k=﹣ ,
,
所以y=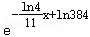 ,
,
该食品在33℃的保鲜时间: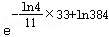 =
= =6(小时).
=6(小时).
故答案为:6.
【点评】本题考查函数的实际意义,函数的解析式的求法,对数运算法则的应用,考查分析问题解决问题的能力,是中档题.
16.(5分)已知双曲线C: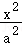 ﹣
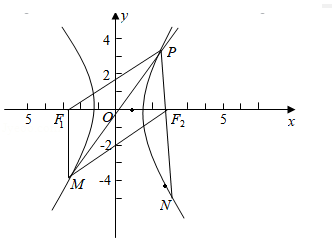
﹣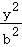 =1(a>0,b>0)的左、右焦点分别为F_1,_F_2,_O为坐标原点,P是双曲线在第一象限上的点,直线PO,PF_2分别交双曲线_C左、右支于另一点M,N,若|PF_1|=2|_PF_2|,且∠_MF_2_N=60°,则双曲线C的离心率为
=1(a>0,b>0)的左、右焦点分别为F_1,_F_2,_O为坐标原点,P是双曲线在第一象限上的点,直线PO,PF_2分别交双曲线_C左、右支于另一点M,N,若|PF_1|=2|_PF_2|,且∠_MF_2_N=60°,则双曲线C的离心率为 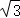 .
.
【考点】KC:双曲线的性质.菁优网版权所有
【分析】由题意,|PF_1|=2|_PF_2|,|_PF_1|﹣|_PF_2|=2_a,可得|PF_1|=4_a,|PF_2|=2_a,由∠MF_2_N=60°,可得∠F_1_PF_2=60°,由余弦定理可得4_c_2=16_a_2+4_a_2﹣2•4_a•2a•cos60°,即可求出双曲线C的离心率.
【解答】解:由题意,|PF_1|=2|_PF_2|,
由双曲线的定义可得,|_PF_1|﹣|_PF_2|=2_a,
可得|PF_1|=4_a,|PF_2|=2_a,
由四边形PF_1_MF_2为平行四边形,
又∠_MF_2_N=60°,可得∠F_1_PF_2=60°,
在三角形_PF_1_F_2中,由余弦定理可得
4_c_2=16_a_2+4_a_2﹣2•4_a•2a•cos60°,
即有4c_2=20_a_2﹣8_a_2,即_c_2=3_a_2,
可得_c= a,
a,
即e=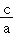 =
= .
.
故答案为: .
.
【点评】本题考查双曲线C的离心率,注意运用双曲线的定义和三角形的余弦定理,考查学生的计算能力,属于中档题.
三、解答题:共70分,解答应写出文字说明、证明过程或演算步骤.第17-21题为必考题,每个考生都必须作答;第22-23题为选考题,考生根据要求作答.(一)必考题:60分
17.(12分)已知a,b,c分别为锐角△ABC三个内角A,B,C的对边,满足sin2A﹣sin2B﹣sin2C+sinB_sin_C=0.
(1)求A;
(2)若b=2,求△ABC面积的取值范围.
【考点】HP:正弦定理.菁优网版权所有
【分析】(1)由已知及正弦定理得a_2=_b_2+_c_2﹣_bc,由余弦定理可得 ,结合范围0<A<π,可求A的值.
,结合范围0<A<π,可求A的值.
(2)由已知及正弦定理得,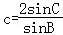 ,由
,由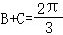 ,利用三角形的面积公式可求S=
,利用三角形的面积公式可求S=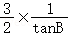 +
+ ,结合△ABC是锐角三角形,可求范围
,结合△ABC是锐角三角形,可求范围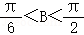 ,利用正切函数的图象和性质即可求解其取值范围.
,利用正切函数的图象和性质即可求解其取值范围.
【解答】解:(1)由已知及正弦定理得,a_2=_b_2+_c_2﹣_bc,
由余弦定理可得 ,
,
又0<A<π,
可得 .
.
(2)由已知及正弦定理得, ,
,
由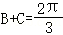 ,得
,得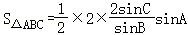 =
=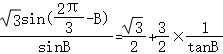 ,
,
△ABC是锐角三角形,得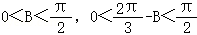 ,得
,得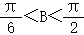 ,
,
∴ ,
,
∴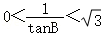 ,
,
∴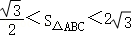 .
.
∴△ABC面积的取值范围是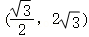 .
.
【点评】本题主要考查了正弦定理,余弦定理,三角形的面积公式,正切函数的图象和性质在解三角形中的综合应用,考查了转化思想和函数思想,属于中档题.
18.(12分)如图△PAD中,∠PDA=90°,DP=DA=2,B、C分别是PA、PD的中点,将△PBC沿BC折起,连结PA、PD,得到多面体PABCD.
(1)证明:在多面体PABCD中,BC⊥PD;
(2)在多面体PABCD中,当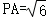 时,求二面角B﹣PA﹣D的余弦值.
时,求二面角B﹣PA﹣D的余弦值.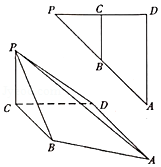
【考点】LW:直线与平面垂直;MJ:二面角的平面角及求法.菁优网版权所有
【分析】(1)先证明BC⊥平面PCD,再利用线面垂直的性质即可得证;
(2)建立空间直角坐标系,求出平面PAB及平面PAD的法向量,利用向量的夹角公式即可得解.
【解答】(1)证明:△PAD中,因为B,C分别是PA,PD的中点,∠PDA=90°,
所以BC∥AD,∠BCP=∠BCD=90°,……………………(1分)
所以多面体PABCD中,BC⊥PC,BC⊥CD,PC∩CD=C,……………………(2分)
∴BC⊥平面PCD.……………………(3分)
又PD⊂平面PCD,
∴BC⊥PD.……………………(4分)
(2)依题意可得,PC=CD=1,直角△ADC中,得 ,又
,又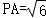 ,
,
所以PA_2=_PC_2+_AC_2,∴_PC⊥CA,……………………(5分)
由(1)知,BC⊥PC,∴PC⊥平面ABCD.……………………(6分)
以C为坐标原点,分别以CB,CD,CP为x,y,z轴,建立如图的坐标系.……………………(7分)
则B(1,0,0),A(2,1,0),D(0,1,0),P(0,0,1),……………………(8分)
得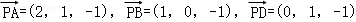 .……………………(9分)
.……………………(9分)
设平面PAB,PAD的一个法向量分别是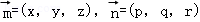 ,
,
则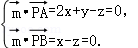 可取
可取 .……………………(10分)
.……………………(10分) 可取
可取 .……………………(11分)
.……………………(11分)
∴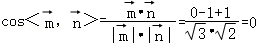 .……………………(12分)
.……………………(12分)
所以二面角B﹣PA﹣D的余弦值为0.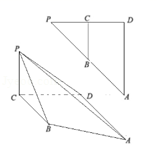
【点评】本题考查线面垂直的判定定理及性质定理的运用,考查利用空间向量求解二面角问题,考查运算求解能力及逻辑推理能力,属于中档题.
19.(12分)某市《城市总体规划(2016﹣2035年)》提出到2035年实现“15分钟社区生活圈”全覆盖的目标,从教育与文化、医疗与养老、交通与购物、休闲与健身4个方面构建“15分钟社区生活圈”指标体系,并依据“15分钟社区生活圈”指数高低将小区划分为:优质小区(指数为0.6~1)、良好小区(指数为0.4~0.6)、中等小区(指数为0.2~0.4)以及待改进小区(指数为0~0.2)4个等级.下面是三个小区4个方面指标的调查数据:
小区 指标值 权重 |
A小区 |
B小区 |
C小区 |
|---|---|---|---|
| 教育与文化(0.20) | 0.7 | 0.9 | 0.1 |
| 医疗与养老(0.20) | 0.7 | 0.6 | 0.3 |
| 交通与购物(0.32) | 0.5 | 0.7 | 0.2 |
| 休闲与健身(0.28) | 0.5 | 0.6 | 0.1 |
注:每个小区“15分钟社区生活圈”指数T=_w_1_T_1+_w_2_T_2+_w_3_T_3+_w_4_T_4,其中_w_1,_w_2,_w_3,_w_4为该小区四个方面的权重,_T_1,_T_2,_T_3,_T_4为该小区四个方面的指标值(小区每一个方面的指标值为0~1之间的一个数值).
现有100个小区的“15分钟社区生活圈”指数数据,整理得到如下频数分布表:
| 分组 | [0,0.2) | [0.2,0.4) | [0.4,0.6) | [0.6,0.8) | [0.8,1] |
|---|---|---|---|---|---|
| 频数 | 10 | 20 | 30 | 30 | 10 |
(Ⅰ)分别判断A,B,C三个小区是否是优质小区,并说明理由;
(Ⅱ)对这100个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取10个小区进行调查,若在抽取的10个小区中再随机地选取2个小区做深入调查,记这2个小区中为优质小区的个数为ξ,求ξ的分布列及数学期望.
【考点】B7:分布和频率分布表;BC:极差、方差与标准差;BL:独立性检验;CH:离散型随机变量的期望与方差.菁优网版权所有
【分析】(Ⅰ)分别求出A、B、C三个小区指数,由此能判断A,B,C三个小区是否是优质小区.
(Ⅱ)对这100个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取10个小区进行调查,抽到优质小区的个数为4个,抽到良好小区的个数为3个,抽到中等小区的个数为2个,抽到待改进小区的个数为1个,在抽取的10个小区中再随机地选取2个小区做深入调查,记这2个小区中为优质小区的个数为ξ,则ξ的可能取值为0,1,2,分别求出相应的概率,由此能求出ξ的分布列和数学期望Eξ.
【解答】解:(Ⅰ)A小区指数为:TA=0.2×0.7+0.2×0.7+0.32×0.5+0.28×0.5=0.58<0.6,
∴A小区不是优质小区.
B小区指数为:TB=0.2×0.9+0.2×0.6+0.32×0.7+0.28×0.6=0.692>0.6,
∴B小区是优质小区.
C小区指数为:TC=0.2×0.1+0.2×0.3+0.32×0.2+0.28×0.1=0.172<0.6,
∴C小区不是优质小区.
(Ⅱ)对这100个小区按照优质小区、良好小区、中等小区和待改进小区进行分层抽样,抽取10个小区进行调查,
抽到优质小区的个数为:10×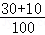 =4个,
=4个,
抽到良好小区的个数为:10×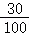 =3个,
=3个,
抽到中等小区的个数为:10× =2个,
=2个,
抽到待改进小区的个数为: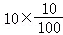 =1个,
=1个,
在抽取的10个小区中再随机地选取2个小区做深入调查,记这2个小区中为优质小区的个数为ξ,
则ξ的可能取值为0,1,2,
P(ξ=0)=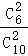 =
=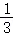 ,
,
P(ξ=1)=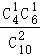 =
=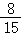 ,
,
P(ξ=2)=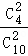 =
=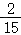 ,
,
∴ξ的分布列为:
| ξ | 0 | 1 | 2 |
|---|---|---|---|
| P | 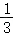 |
 |
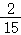 |
数学期望Eξ=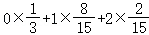 =
=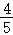 .
.
【点评】本题考查优质小区的判断,考查离散型随机变量的分布列、数学期望的求法,考查古典概型、排列组合等基础知识,考查学生的逻辑分析能力、运算求解能力,是中档题.
20.(12分)已知两动圆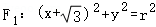 和
和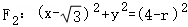 (0<r<4),把它们的公共点的轨迹记为曲线C,若曲线C与y轴的正半轴的交点为M,且曲线C上的相异两点A、B满足:
(0<r<4),把它们的公共点的轨迹记为曲线C,若曲线C与y轴的正半轴的交点为M,且曲线C上的相异两点A、B满足: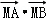 =0.
=0.
(1)求曲线C的方程;
(2)证明直线AB恒经过一定点,并求此定点的坐标;
(3)求△ABM面积S的最大值.
【考点】9O:平面向量数量积的性质及其运算;JE:直线和圆的方程的应用.菁优网版权所有
【分析】(1)设两动圆的公共点为Q,则有|QF_1|+|_QF_2|=4,运用椭圆的定义,即可得到_a,c,b,进而得到Q的轨迹方程;
(2)M(0,1),设A(x_1,_y_1),_B(x_2,_y_2),根据直线_AB的斜率不存在和存在,设出直线方程,根据条件,运用向量的数量积的坐标表示,结合韦达定理和直线恒过定点的求法,即可得到定点;
(3)△ABM面积S=S△MNA+S△MNB=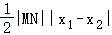 ,代入韦达定理,化简整理,结合N在椭圆内,运用对勾函数的单调性,即可得到最大值.
,代入韦达定理,化简整理,结合N在椭圆内,运用对勾函数的单调性,即可得到最大值.
【解答】解:(1)设两动圆的公共点为Q,则有|QF_1|+|_QF_2|=4(4>|_F_1_F_2|).
由椭圆的定义可知_Q的轨迹为椭圆,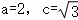 .b=
.b=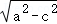 =1,
=1,
所以曲线C的方程是: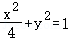 .
.
(2)证明:由题意可知:M(0,1),设A(x_1,_y_1),_B(x_2,_y_2),
当_AB的斜率不存在时,易知满足条件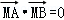 的直线AB为:x=0,过定点
的直线AB为:x=0,过定点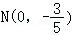 ;
;
当AB的斜率存在时,设直线AB:y=kx+m,联立方程组: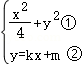 ,
,
把②代入①有:(1+4k_2)_x_2+8_kmx+4m_2﹣4=0,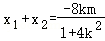 ③,
③,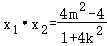 ④,
④,
因为 ,所以有_x_1•_x_2+(_kx_1+_m﹣1)(kx_2+_m﹣1)=0,
,所以有_x_1•_x_2+(_kx_1+_m﹣1)(kx_2+_m﹣1)=0,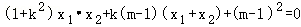 ,
,
把③④代入整理: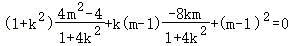 ,
,
(有公因式m﹣1)继续化简得(m﹣1)(5m+3)=0, 或m=1(舍),
或m=1(舍),
综合斜率不存在的情况,直线AB恒过定点 .
.
(3)△ABM面积S=S△MNA+S△MNB=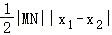 =
=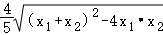 ,
,
由第(2)小题的③④代入,整理得: ,
,
因N在椭圆内部,所以k∈R,可设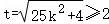 ,
, =
=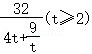 ,
,
∵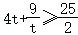 ,∴
,∴ (k=0时取到最大值).
(k=0时取到最大值).
所以△ABM面积S的最大值为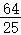 .
.
【点评】本题考查椭圆的定义、方程和性质,主要考查椭圆的定义、方程的运用,同时考查平面向量的数量积的坐标表示和直线恒过定点的求法,以及函数的单调性的运用,属于中档题和易错题.
21.(12分)已知函数f(x)=2lnx﹣ax_2+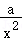 .
.
(1)当0<_a<1时,求证: ;
;
(2)当f(x)有三个零点时,求a的取值范围.
【考点】52:函数零点的判定定理;6B:利用导数研究函数的单调性.菁优网版权所有
【分析】(1)令t=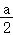 ,构造函数g(t)=2lnt﹣2t_3+
,构造函数g(t)=2lnt﹣2t_3+ ,求函数的导数,利用导数研究函数的单调性即可得到结论.
,求函数的导数,利用导数研究函数的单调性即可得到结论.
(2)构造函数_h(x)=lnx﹣ax+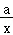 ,求函数的导数,利用导数研究函数的单调性,结合函数零点关系分别进行讨论即可.
,求函数的导数,利用导数研究函数的单调性,结合函数零点关系分别进行讨论即可.
【解答】解:(1)证明:f(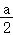 )=2ln
)=2ln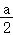 ﹣a(
﹣a(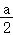 )2+
)2+ ,
,
令t=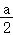 ,则0<t<
,则0<t<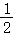 ,
,
则f(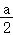 )=g(t)=2lnt﹣2t_3+
)=g(t)=2lnt﹣2t_3+ ,
,
导数_g′(t)= ﹣6t_2﹣
﹣6t_2﹣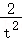 =
=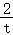 (1﹣
(1﹣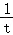 )﹣6_t_2<0,
)﹣6_t_2<0,
即_g(t)在0<t<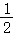 上单调递减,
上单调递减,
则g(t)>g(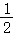 )=2ln
)=2ln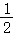 ﹣
﹣ +4=4﹣
+4=4﹣ ﹣2ln_2>0,
﹣2ln_2>0,
则_f( )>0成立,
)>0成立,
所以原命题成立.
(2)由f(x)=2lnx﹣ax_2 =_lnx_2+_ax_2
=_lnx_2+_ax_2 (_x>0)有三个零点可得
(_x>0)有三个零点可得
h(x)=lnx﹣ax+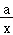 有三个零点,
有三个零点,
h′(x)= ,(x>0)
,(x>0)
①当a≤0吋,h′(x)>0恒成立,可得h(x)至多有一个零点,不符合題意;
②当a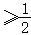 时,h′(x)≤0恒成立,可得h(x)至多有一个零点,不符合題意;
时,h′(x)≤0恒成立,可得h(x)至多有一个零点,不符合題意;
③当0<a<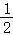 时,记φ(x)=﹣ax_2+_x﹣a,(x>0)得两个零点为x_1,_x_2,不妨没0<_x_1<_x_2,
时,记φ(x)=﹣ax_2+_x﹣a,(x>0)得两个零点为x_1,_x_2,不妨没0<_x_1<_x_2,
且_x_1•_x_2=1,
_x∈(0,x_1)时,_h‘(x)<0; x∈(x_1,_x_2)时,_h′(x)>0; x∈(x_2,+∞)时,_h′(x)<0,
观察可得h(1)=0,且x_1<1<_x_2,
当_x∈(x_1,_x_2)时,_h′(x)>0; h(x)单调递增,
所以有h(x_1)<_h(1)<h(x_2),即_h(x_1)<0<_h(x_2),
_x∈(0,x_1)时,_h′(x)<0,h(x)单调递减,
x∈(x_2,+∞)时,_h′(x)<0,h(x)单调递减,
由(1)知,h(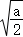 )>0,且h(x_1)<0,所以_h(x)在(
)>0,且h(x_1)<0,所以_h(x)在(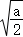 ,x_1)上有一个零点,
,x_1)上有一个零点,
由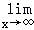 _h(x)→﹣∞,且h(x_2)>0,所以_h(x)在(x_2,+∞)上有一个零点,
_h(x)→﹣∞,且h(x_2)>0,所以_h(x)在(x_2,+∞)上有一个零点,
综上可知_h(x)=lnx﹣ax+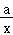 ,(x>0)有三个零点,
,(x>0)有三个零点,
即f(x)=21nx﹣ax_2+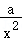 =1_nx_2﹣_ax_2+
=1_nx_2﹣_ax_2+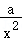 ,(_x>0)有三个零点,
,(_x>0)有三个零点,
所求a的范围是(0,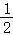 ).
).
【点评】本题主要考查函数零点和方程的应用,构造函数求的导数,研究函数的单调性是解决本题的关键.综合性较强,在求解过程中多次使用构造函数法,有一定的难度.
选考题:10分.请考生在第22、23题中任选一题作答.如果多做,则按所做的第一题计分.[选修4-4:坐标系与参数方程](10分)
22.(10分)以直角坐标系的原点为极点,x轴的非负半轴为极轴,建立极坐标系,并在两种坐标系中取相同的长度单位,已知直线的参数方程为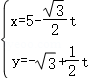 (t为参数),圆C的极坐标方程为
(t为参数),圆C的极坐标方程为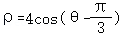 .
.
(1)求直线和圆C的直角坐标方程;
(2)若点P(x,y)在圆C上,求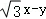 的取值范围.
的取值范围.
【考点】Q4:简单曲线的极坐标方程;QH:参数方程化成普通方程.菁优网版权所有
【分析】(Ⅰ)直线l的参数方程消去参数t,能求出直线l的直角坐标方程;圆C的极坐标方程转化为 ,由ρ2=x_2+_y_2,ρcosθ=_x,ρsinθ=y,能求出圆C的直角坐标方程.
,由ρ2=x_2+_y_2,ρcosθ=_x,ρsinθ=y,能求出圆C的直角坐标方程.
(Ⅱ)设P(1+2cosθ,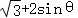 ),则
),则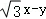 =
= =4sin(θ+
=4sin(θ+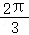 ),由此能求出
),由此能求出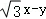 的取值范围.
的取值范围.
【解答】解:(Ⅰ)∵直线l的参数方程为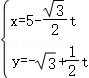 (t为参数),
(t为参数),
∴消去参数t,得直线l的直角坐标方程为x+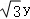 ﹣2=0,
﹣2=0,
∵圆C的极坐标方程为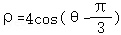 ,
,
∴ ,
,
∵ρ2=x_2+_y_2,ρcosθ=_x,ρsinθ=y,
∴圆C的直角坐标方程为(x﹣1)2+(y﹣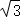 )2=4.
)2=4.
(Ⅱ)∵点P(x,y)在圆C上,
∴设P(1+2cosθ, ),
),
∴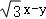 =
=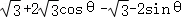 =4sin(θ+
=4sin(θ+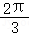 ),
),
∴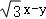 的取值范围是[﹣4,4].
的取值范围是[﹣4,4].
【点评】本题考查直线和圆直角坐标方程的求法,考查代数式的取值范围的求法,考查极坐标方程、直角坐标方程、参数方程的互化等基础知识,考查推理论证能力、运算求解能力,考查化归与转化思想、函数与方程思想,是中档题.
[选修4-5:不等式选讲](10分)
23.已知函数f(x)=|2x+3|﹣|x﹣1|.
(1)求不等式f(x)≤3的解集;
(2)若不等式f(x)>2a﹣|3x﹣3|对任意x∈R恒成立,求实数a的取值范围.
【考点】6P:不等式恒成立的问题;R5:绝对值不等式的解法.菁优网版权所有
【分析】(1)根据f(x)≤3,可得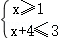 或
或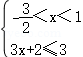 或
或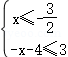 ,然后解不等式组即可得到解集;
,然后解不等式组即可得到解集;
(2)不等式f(x)>2a﹣|3x﹣3|对任意x∈R恒成立,即不等式|2x+3|+|2x﹣2|>2a对x∈R成立,由绝对值三角不等式可得|2x+3|+|2x﹣2|≥5,从而得到2a<5,然后解不等式可得a的范围.
【解答】解:(1)由f(x)≤3,得|2x+3|﹣|x﹣1|≤3,
∴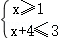 或
或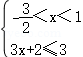 或
或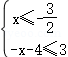 ,
,
∴ 或
或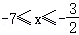 ,
,
∴不等式的解集为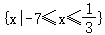 .
.
(2)若不等式f(x)>2a﹣|3x﹣3|对x∈R成立,
即不等式|2x+3|﹣|x﹣1|>2a﹣|3x﹣3|对x∈R成立,
即不等式|2x+3|+|2x﹣2|>2a对x∈R成立,
∵|2x+3|+|2x﹣2|≥|(2x+3)﹣(2x﹣2)|=5,
∴2a<5,∴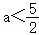 ,
,
∴a的取值范围为(﹣∞,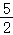 ).
).
【点评】本题考了绝对值不等式的解法和不等式恒成立问题,考查了分类讨论思想和转化思想,属中档题.
声明:试题解析著作权属菁优网所有,未经书面同意,不得复制发布
日期:2020/6/25 20:36:17;用户:17859775485;邮箱:17859775485;学号:21682042

