• 关于贝叶斯，参见https://www.bilibili.com/video/BV1R7411a76r/?spm_id_from=333.788.videocard.0
  3Blue1Brown频道的许多关于数学的内容都深入简出，基于它们开发的一个python库。

贝叶斯公式

贝叶斯公式实际表达即是，在某事件发生的条件下，另一个事件发生的概率。

直观的理解贝叶斯公式

当我们判断一个温和而有涵养的人是什么职业的时候，我们可能更相信他是一个图书馆员，而并非一个农民。
但数据告诉我们，图书馆员相比农民，在人群中所占的比重非常小。（假设图书馆员比农民为1:20）

因此某些直觉的判断可能违背理性。理性不代表知道事实，而是认识到哪些因素是有关的。

• 假设有10个图书馆员，对应200个农民。
  
• 当我们听到关于温和而有涵养的人的描述后，直觉告诉我们有40%的可能他是图书馆员，而10%的可能他是农民。
• 因此我们可以得到预计的相应总体中的人数。
  
• 并且可以得到判断在该样本大小写，符合该描述的图书馆员所占的比重。
  

贝叶斯公式的核心思想

新证据并不能直接凭空决定你的看法，而是应该更新你之前的看法。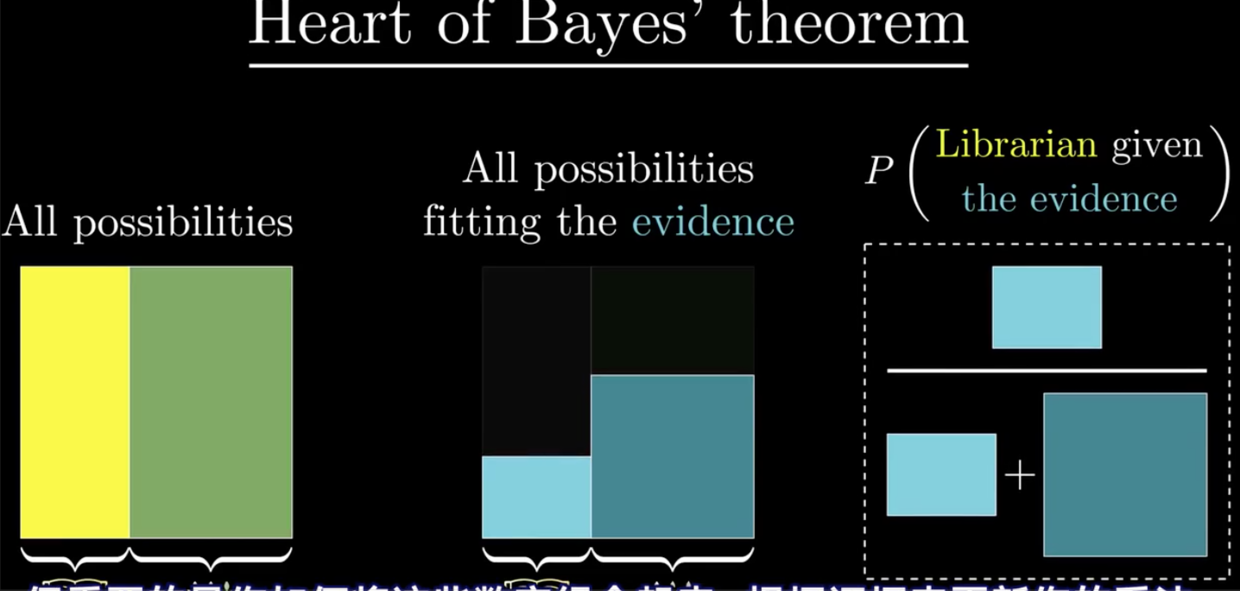

贝叶斯公式的数学表达

目标结果

| 之前的内容为之后内容的限制因素，即 hypothesis 的概率是在符合E 的基础之上得到的。

先验概率 prior

图书馆员所占总数的比为10:(10 + 200)

似然概率 likelihood

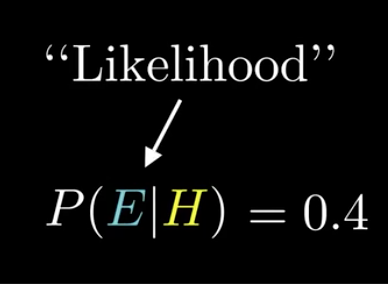
假设为图书馆员的条件下，符合角色描述的概率。

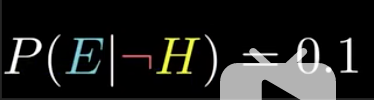
假设为农民的条件下，符合角色描述的概率。（H 之前的符号表示为非）

后验概率 posterior

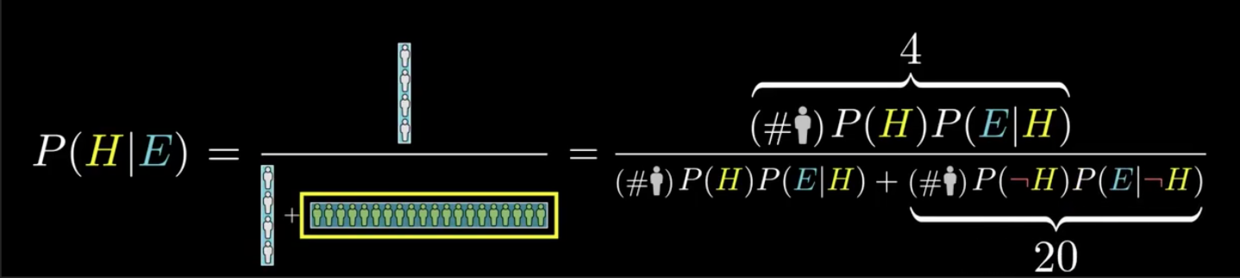
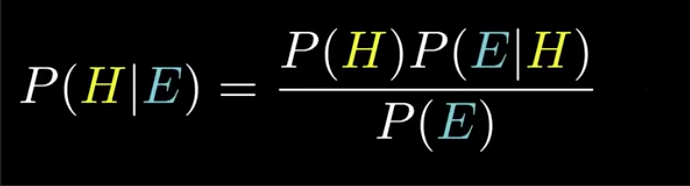
首先可以约去上下的人数，接着可以将分母内容用P(E) 表示，代表看到所有证据的概率（即所有假设下的所有符合证据的个数）。

总结

我们可以将任何事件都对应概率空间的一个子集（一个1X1 的正方形），概率的大小可以通过划分正方形的面积来表示。

贝叶斯公式的延展

这里再引入之前的图书馆员和农民的例子，再加一个商人。
可以理解成在某个先验概率情况下，分割长方形（先验概率，农民、商人、图书馆员占其总人群的比例）。再对长方形根据似然概率的描述，得到具体的面积（符合某种描述的人群的概率）。其中符合特定要求（图书馆员）的特定描述的面积所占全部（农民、商人、图书馆员概率之和）的符合特定描述的面积的比例，即为该特定描述下特定要求（图书馆员）所占的比例。

练习题

贝叶斯公式在生物学中的应用