进制那点事儿

数字虽然被分成不同的进制形式表示，但是其实际意义一样大，只是表示形式不一样。每类进制数的特点是，每一位都不准超过该类进制对应的值，如我们常用的是十进制数，逢10就进1，一位的最大数字是9，二进制数，一位对应的最大数字是1，十六进制的一位表示的最大数字是15，八进制的是7，规则是一样的。

1. 二进制与十进制间不得不说的事

关于数字，我们常用的是十进制的数字，但是计算机只能识别二进制的机器语言，二进制下的数字只有0或1两种形式，因为计算机的存储原理是用高电平和低电平两种电平来存储0和1。只要涉及到和电脑打交道，就必须面临二进制与十进制间的相互转换，具体转换方式如下：

1.1 二进制转十进制

二进制转化为十进制有两种方法，如下所示：

1) 通用法：(2)表示该数字是用二进制表示的数字，(10)表示十进制数，转化即如下例所示：

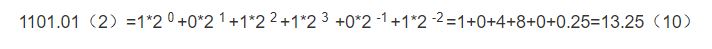
分别是在小数点前面的整数，从右往左为，2,2,2……，再依次乘以对应位的数字，小数部分，是从左往右为2，2，2……，再依次乘以对应位置的数字，最后相加即可。

2) 取巧法：，记住每一位对应的十进制数，即2=1，2=2，2=4…..，然后按位相加即可。整数部分从右往左如下所示：

1 1 1 1 1 1 1 1 .(小数点)
128 64 32 16 8 4 2 1 .(小数点)

如一个二进制数为1101，则按照上面所示将对应位置为1的数字按位相加为 1+4+8=13(10)

1.2 十进制转二进制

十进制转二进制也有两种方法，如下所示：

1) 通用法：也叫除2取余，逆序排列法，下图来源百度，具体如下：

2) 取巧法：**和上述的二进制取巧法一样，记住前8位置，每位对应的十进制数

1 1 1 1 1 1 1 1 .(小数点)
128 64 32 16 8 4 2 1 .(小数点)

然后这8位，最大表示的十进制数是最高位的前一位置对应的数字减1，即2-1=255，这八位二进制数表示的最大整数是255，所以例如对于255以下的十进制数的转化，如173，则按照上述位置得128+32+8+4+1=173，则对应的二进制数为10101101。

2. 二进制与十六进制间不得不说的事

从上述二进制与十进制的转换可知，若一个很大的十进制数用二进制表示的话，需要很长一串二进制数字，电脑可以，人手写存入可麻烦了，因此便有了新的进制，十六进制和八进制。这里介绍十六进制和二进制的关系，八进制和其思想一样。具体转化如下：

2.1 二进制转十六进制

低位往高位转是比较好转的，十六进制数是每4位二进制数是一位十进制数，4位二进制数可表示的十进制数最小为0，最大为1111(2)=1+2+4+8=15，符合十六进制的标准，但是进制数只能一位表示一个数，因此十六进制的基数为0、 1、2、3、4、5、6、7、8、9、A(10)、B(11)、C(12)、D(13)、E(14)、F(15)。二进制转十六进制，每四位为一组，从后往前取，不足的补0。例如：11010011分为1101(2)=13=D，0011=3即11010011(2)=D3。

2.2 十六进制转二进制

一个十六进制数对应四位二进制数，

1 1 1 1 .(小数点)
8 4 2 1 .(小数点)

如十六进制数3FD即，3(8)=0011，F(8)=1111，D(8)=1101，则3DF(8)=001111111101(2)。

3. 二进制与八进制间的转换

和二进制与十六进制的转换类似，八进制数是对应3个二进制数。基数为0、1、2、3、4、5、6、7。

4. 十六进制、八进制与十进制的转换

那就先将十六进制转化成二进制，再转化成十进制，这样最容易。