概念

Trie 树，也叫“字典树”。它是一种专门处理字符串匹配的数据结构，用来解决在一组字符串集合中快速查找某个字符串的问题。当然，这样一个问题可以有多种解决方法，比如散列表、红黑树、字符串匹配算法等等，但是Trie 树在这个问题的解决上，有它特有的优点。
举例：有 6 个字符串，分别是：how，hi，her，hello，so，see。如果多次查找某个字符串是否存在，每次查找，都是拿要查找的字符串跟这 6 个字符串依次进行字符串匹配，那效率就比较低。
这时就可以先对这 6 个字符串做一下预处理，组织成 Trie 树的结构，之后每次查找，都是在 Trie 树中进行匹配查找。Trie 树的本质，就是利用字符串之间的公共前缀，将重复的前缀合并在一起。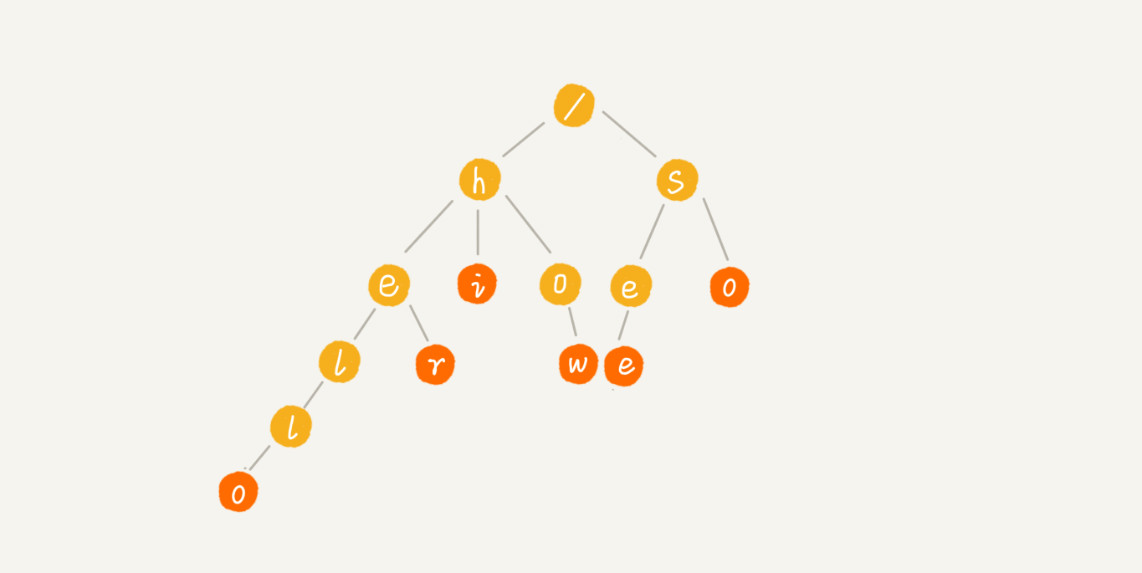
image.png
其中，根节点不包含任何信息。每个节点表示一个字符串中的字符，从根节点到红色节点的一条路径表示一个字符串（注意：红色节点并不都是叶子节点）。
Trie 树构造的过程：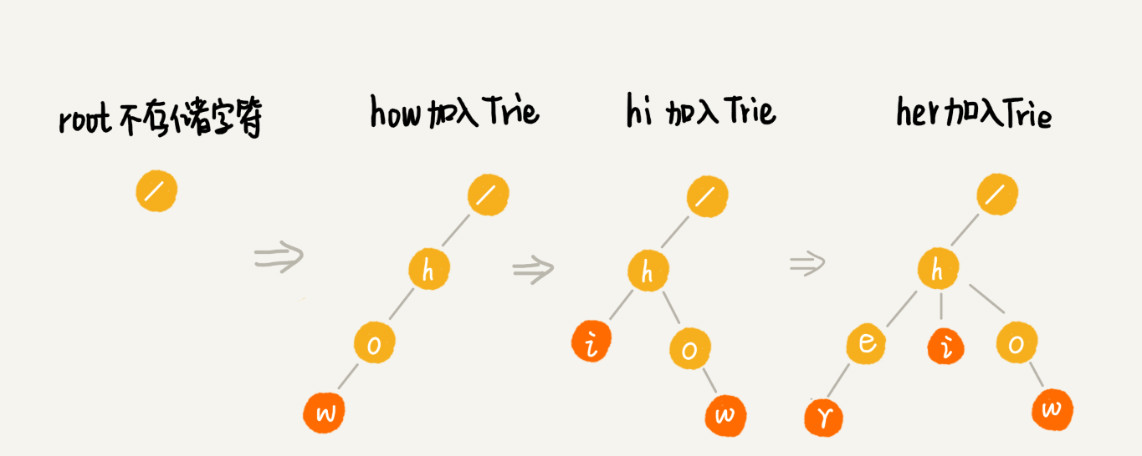
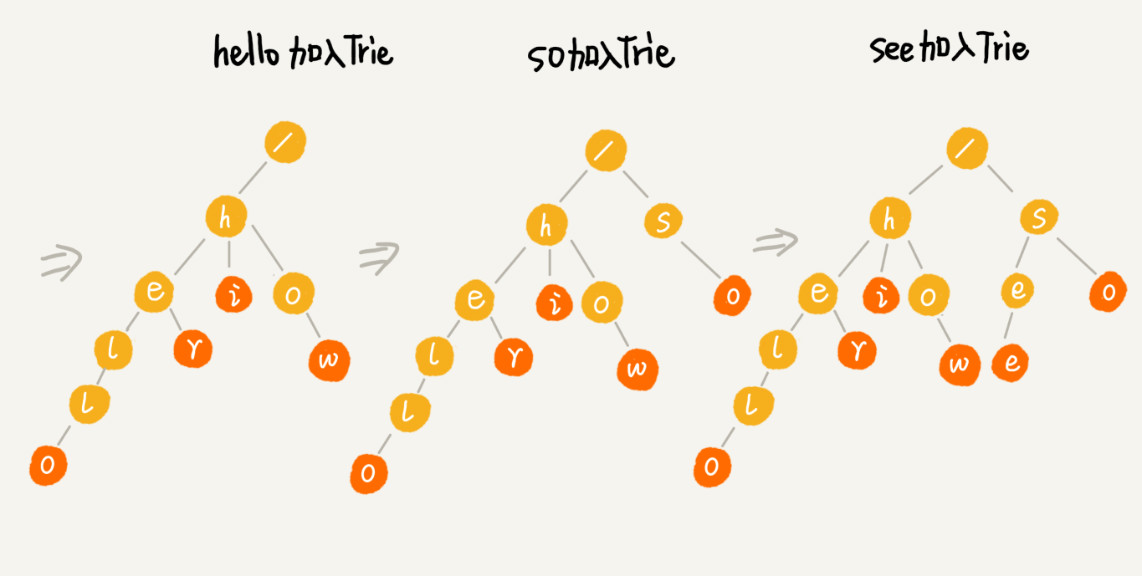
image.pngimage.png
当查找字符串“her”，那我们将要查找的字符串分割成单个的字符 h，e，r，然后从 Trie 树的根节点开始匹配。如图所示，绿色的路径就是在 Trie 树中匹配的路径。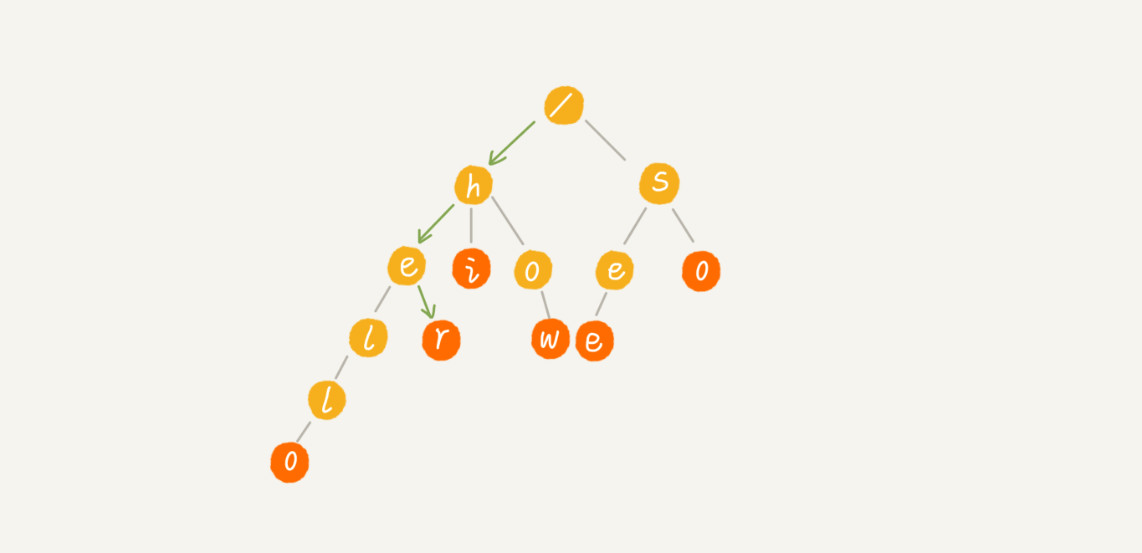
image.png
如要查找的是字符串“he”，从根节点开始，沿着某条路径来匹配，如图所示，绿色的路径，是字符串“he”匹配的路径。但是，路径的最后一个节点“e”并不是红色的。也就是说，“he”是某个字符串的前缀子串，但并不能完全匹配任何字符串。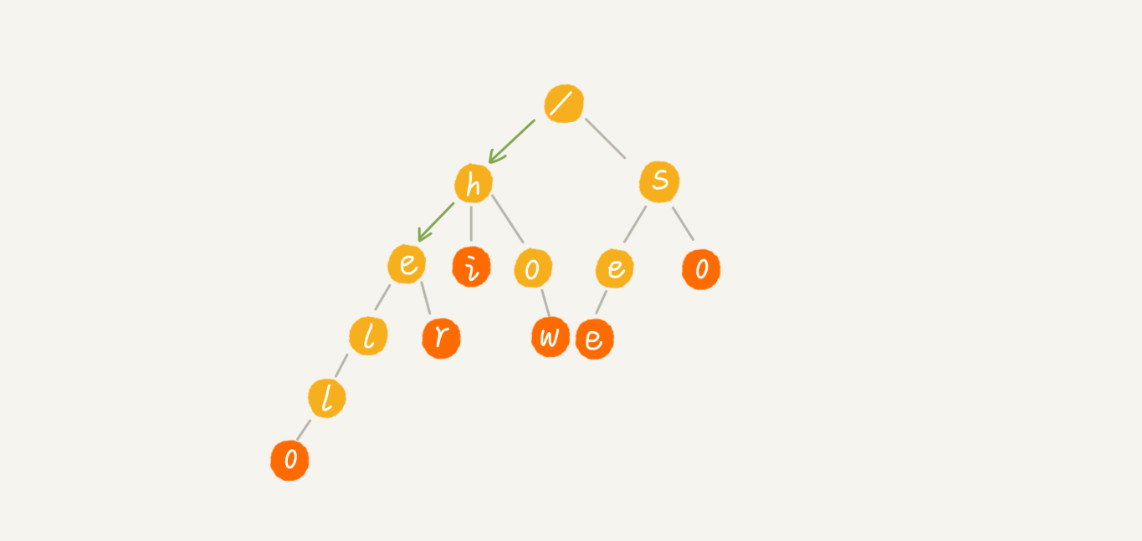
image.png

代码实现

  1. class Trie {
  2.   constructor() {
  3.     this.data = {}
  4.   }
  6.   // 插入一个单词
  7.   insert(word) {
  8.     let node = this.data
  9.     for (let c of word) {
  10.       if (node[c]) {
  11.         node = node[c]
  12.       } else {
  13.         node[c] = {}
  14.         node = node[c]
  15.       }
  16.     }
  17.     //通过isEnd标记是否是一个完整的单词
  18.     node['isEnd'] = true
  19.   }
  21.   search(word) {
  22.     let node = this.data
  23.     for (let c of word) {
  24.       if (!node[c]) {
  25.         //trie找不到那个字母也返回false
  26.         return false
  27.       }
  28.       node = node[c]
  29.     }
  30.     //没有这个属性就返回fasle，有就放回true
  31.     return !!node['isEnd']
  32.   }
  34.   // 查找trie中是否存在word的前缀,匹配则返回匹配的节点，方便后续的查找。
  35.   startWith(word) {
  36.     let node = this.data
  37.     for (let c of word) {
  38.       if (!node[c]) {
  39.         return false
  40.       }
  41.       node = node[c]
  42.     }
  43.     return node
  44.   }
  46.   // 查找后续单词
  47.   findSuffix(word) {
  48.     //递归查找
  49.     function findAll(prefix, node, arr = [prefix]) {
  50.       for (let key in node) {
  51.         if (key !== 'isEnd') {
  52.           let word = prefix + key
  53.           arr.push(word)
  54.           findAll(word, node[key], arr)
  55.         }
  56.       }
  57.       return arr
  58.     }
  59.     let node = this.startWith(word)
  60.     if (!node) {
  61.       return false
  62.     }
  63.     return findAll(word, node)
  64.   }
  65. }
  67. let trie = new Trie()
  68. trie.insert('apple')
  69. console.log(JSON.stringify(trie.data))//{"a":{"p":{"p":{"l":{"e":{"isEnd":true}}}}}}
  70. trie.insert('acc')
  71. console.log(JSON.stringify(trie.data))//{"a":{"p":{"p":{"l":{"e":{"isEnd":true}}}},"c":{"c":{"isEnd":true}}}}
  72. console.log(trie.search('app'))// false
  73. console.log(trie.search('apple'))// true
  74. console.log(trie.startWith('acc'))//false
  75. console.log(trie.startWith('app'))//{ l: { e: { isEnd: true } } }
  76. console.log(trie.startWith('apple'))//{ isEnd: true }
  77. console.log(trie.findSuffix('app'))//[ 'app', 'appl', 'apple' ]

复杂度

时间复杂度：构建 Trie 树的过程，需要扫描所有的字符串，时间复杂度是 O(n)（n 表示所有字符串的长度和）。构建好 Trie 树后，在其中查找字符串的时间复杂度是 O(k)（k 表示要查找的字符串的长度）。
空间复杂度：字典树每个节点都需要用一个数组/对象来存储子节点的指针，所以字典树比较耗内存，空间复杂度较高。
如何优化？

  1. 可以牺牲一点查询的效率，将每个节点的子节点数组用其他数据结构代替，例如有序数组，红黑树，散列表等，当子节点数组采用有序数组时，可以使用二分查找来查找下一个字符。
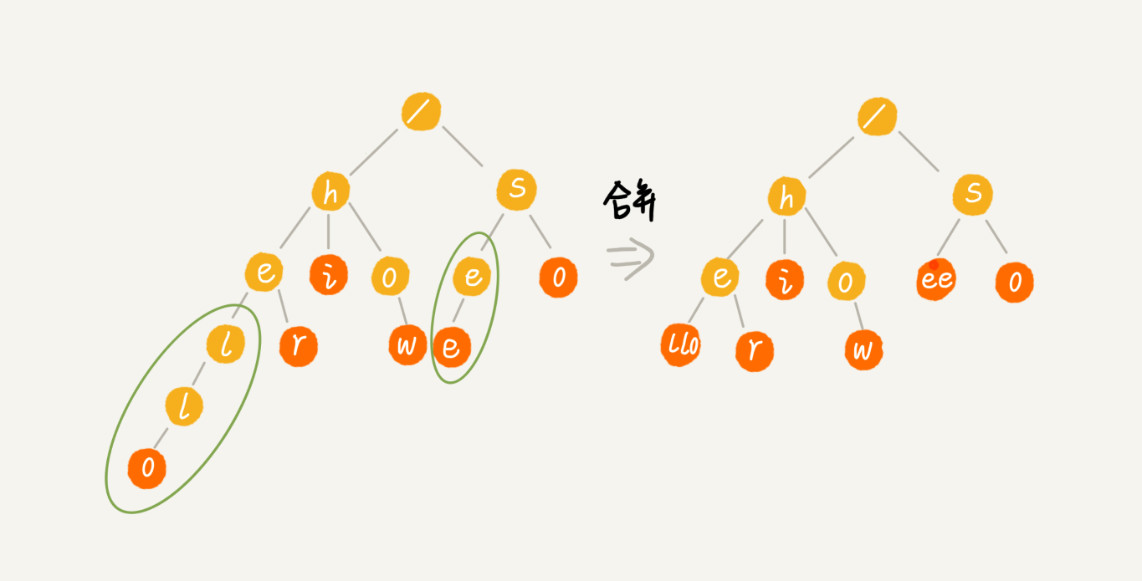
  2. 缩点优化。将末尾一些只有一个子节点的节点，可以进行合并，但是增加了编码的难度。如图

image.png

Trie 树与散列表、红黑树的比较

字典树的缺陷：

  • 需要处理的字符串的字符集不能过大，否则存储空间过于浪费，即便是采用优化方案，也是在牺牲部分查询性能的基础上的
  • 在字符串前缀重合较多的情况，才有比较好的性能表现，不然空间消耗会变大很多。
  • 没有现成的字典树可以用，如果要使用需要手写实现Trie树，还要保证没有bug。
  • 字典树中使用到了指针，通过指针串起来的数据块是不连续的，因此前后节点是不连续的，对 CPU 缓存不友好

综上：在字符串的精确查找场景中，推荐使用红黑树，散列表等数据结构。而字典树，则适合在查找前缀的场景下，例如，搜索引擎一般在输入部分字符后，会显示一些预选关键字。这些关键字均是以输入的字符为前缀。image.png