问题引申

网页爬虫是搜索引擎中非常重要的系统，负责爬取几十亿、上百亿的网页。爬虫的工作原理是，通过解析已经爬取页面中的网页链接，然后再爬取这些链接对应的网页。同一个网页链接有可能被包含在多个页面中，这就会导致爬虫在爬取的过程中，重复爬取相同的网页。如何避免这些重复的爬取呢？
这个问题要处理的对象是网页链接URL，需要支持的操作有两个，添加一个 URL 和查询一个 URL。除了这两个功能性的要求之外，在非功能性方面还要求这两个操作的执行效率要尽可能高。除此之外，因为处理的是上亿的网页链接，内存消耗会非常大，所以在存储效率上要尽可能地高效。
显然，散列表、红黑树、跳表这些动态数据结构，都能支持快速地插入、查找数据，但是对内存消耗方面，是否可以接受呢？
拿散列表来举例。假设要爬取 10 亿个网页，为了判重，把这 10 亿网页链接存储在散列表中。假设一个 URL 的平均长度是 64 字节，单纯存储这 10 亿个 URL，需要大约 60GB 的内存空间。因为散列表必须维持较小的装载因子，才能保证不会出现过多的散列冲突，导致操作的性能下降。而且，用链表法解决冲突的散列表，还会存储链表指针。所以，如果将这 10 亿个 URL 构建成散列表，那需要的内存空间会远大于 60GB，有可能会超过 100GB。当然对于一个大型的搜索引擎来说，即便是 100GB 的内存要求，其实也不算太高，可以采用分治的思想，用多台机器来存储这 10 亿网页链接。
不过，在添加、查询数据的效率以及内存消耗方面，是否还有进一步的优化空间呢？

算法解析

位图（BitMap）

位图就是一种比较“特殊”的散列表。
假设有 1 千万个整数，整数的范围在 1 到 1 亿之间。如何快速查找某个整数是否在这 1 千万个整数中呢？
那就是申请一个大小为 1 亿、数据类型为布尔类型（true 或者 false）的数组。将这 1 千万个整数作为数组下标，将对应的数组值设置成 true。比如整数 5 对应下标为 5 的数组值设置为 true，也就是array[5]=true。查询只需要将对应的数组值 array[K] 取出来，看是否等于 true。如果等于 true，那说明 1 千万整数中包含这个整数 K；相反，就表示不包含这个整数 K。
不过，很多语言中提供的布尔类型，大小是 1 个字节的，并不能节省太多内存空间。实际上，表示 true 和 false 两个值，只需要用一个二进制位（bit）就可以了。那如何通过编程语言，来表示一个二进制位呢？
位图通过数组下标来定位数据，访问效率非常高。而且，每个数字用一个二进制位来表示，在数字范围不大的情况下，所需要的内存空间非常节省。比如用散列表存储这 1 千万的数据，数据是 32 位的整型数，也就是需要 4 个字节的存储空间，那总共至少需要 40MB 的存储空间。如果通过位图的话，数字范围在 1 到 1 亿之间，只需要 1 亿个二进制位，也就是 12MB 左右的存储空间就够了。

布隆过滤器（Bloom Filter）

布隆过滤器本身就是基于位图的，是对位图的一种改进。
位图的局限性就是数字所在的范围不能很大。如果数字的范围很大，不是 1 到 1 亿，而是 1 到 10 亿，那位图的大小就是 10 亿个二进制位，也就是 120MB 的大小，消耗的内存空间，不降反增。
布隆过滤器的做法是，仍然使用一个 1 亿个二进制大小的位图，然后通过哈希函数，对数字进行处理，让它落在这 1 到 1 亿范围内。比如把哈希函数设计成 f(x)=x%n，x 表示数字，n 表示位图的大小（1 亿），也就是，对数字跟位图的大小进行取模求余。
不过哈希函数会存在冲突的问题，一亿零一和 1 两个数字，经过刚刚那个取模求余的哈希函数处理之后，最后的结果都是 1。这样我就无法区分，位图存储的是 1 还是一亿零一了。既然一个哈希函数可能会存在冲突，那用多个哈希函数一块儿定位一个数据，降低冲突的概率。
使用 K 个哈希函数，对同一个数字进行求哈希值，那会得到 K 个不同的哈希值，分别记作 X1，X2，X3，…，XK。把这 K 个数字作为位图中的下标，将对应的 BitMap[X1]，BitMap[X2]，BitMap[X3]，…，BitMap[XK] 都设置成 true，也就是说，用 K 个二进制位，来表示一个数字的存在。当要查询某个数字是否存在的时候，用同样的 K 个哈希函数，对这个数字求哈希值，分别得到 Y1，Y2，Y3，…，YK。看这 K 个哈希值，对应位图中的数值是否都为 true，如果都是 true，则说明，这个数字存在，如果有其中任意一个不为 true，那就说明这个数字不存在。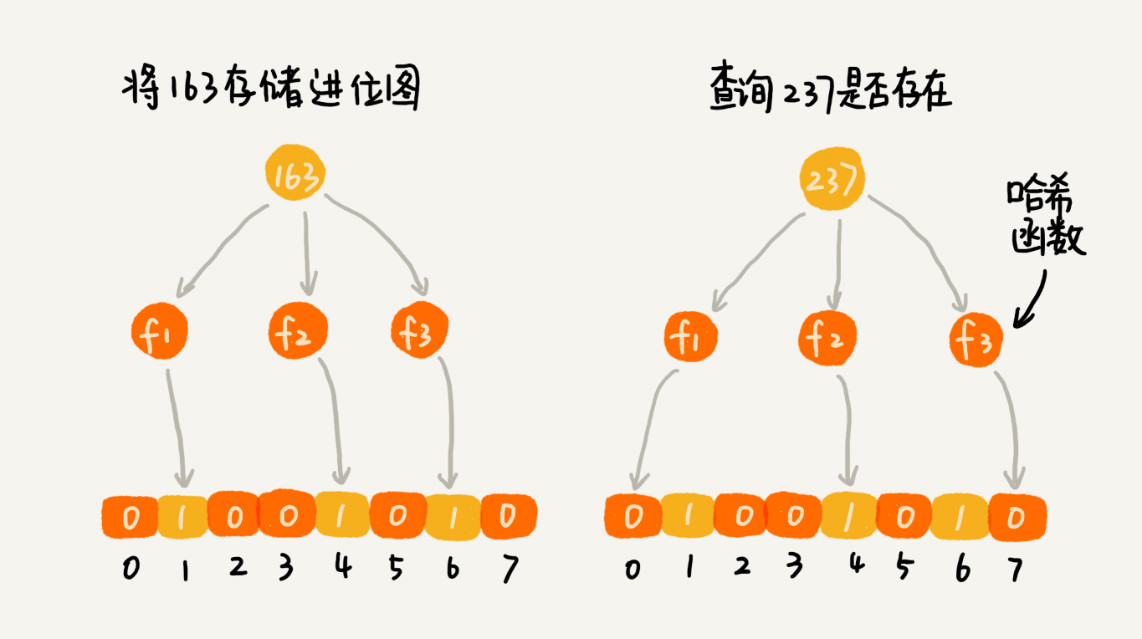

对于两个不同的数字来说，经过一个哈希函数处理之后，可能会产生相同的哈希值。但是经过 K 个哈希函数处理之后，K 个哈希值都相同的概率就非常低了。尽管采用 K 个哈希函数之后，两个数字哈希冲突的概率降低了，但是，这种处理方式又带来了新的问题，那就是容易误判。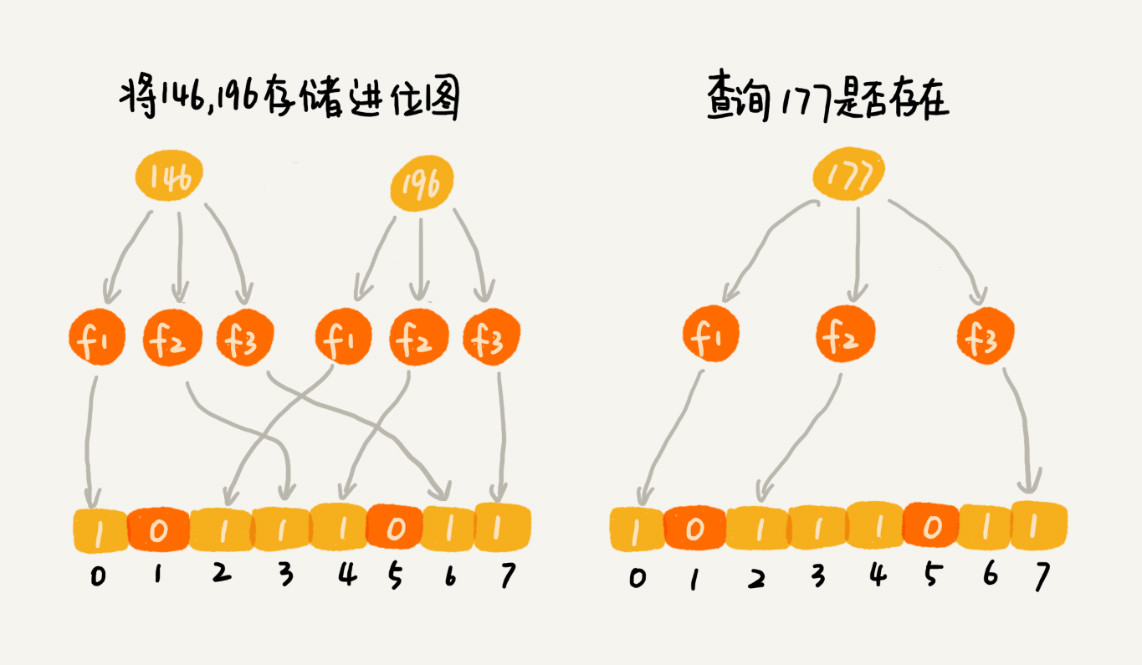

布隆过滤器的误判有一个特点，它只会对存在的情况有误判。如果某个数字经过布隆过滤器判断不存在，那说明这个数字真的不存在，不会发生误判；如果某个数字经过布隆过滤器判断存在，这个时候才会有可能误判，有可能并不存在。不过，只要我们调整哈希函数的个数、位图大小跟要存储数字的个数之间的比例，那就可以将这种误判的概率降到非常低。bloom filter: False is always false. True is maybe true.

爬虫判重这个问题，即便一个没有被爬取过的网页，被误判为已经被爬取，对于搜索引擎来说，也并不是什么大事情，是可以容忍的，毕竟网页太多了，搜索引擎也不可能 100% 都爬取到。用布隆过滤器来记录已经爬取过的网页链接，假设需要判重的网页有 10 亿，那可以用一个 10 倍大小的位图来存储，也就是 100 亿个二进制位，大约 1.2GB。之前我们用散列表判重，需要至少 100GB 的空间。相比来讲，布隆过滤器在存储空间的消耗上，降低了非常多。
布隆过滤器用多个哈希函数对同一个网页链接进行处理，CPU 只需要将网页链接从内存中读取一次，进行多次哈希计算，理论上讲这组操作是 CPU 密集型的。而在散列表的处理方式中，需要读取散列冲突拉链的多个网页链接，分别跟待判重的网页链接，进行字符串匹配。这个操作涉及很多内存数据的读取，所以是内存密集型的。CPU 计算可能是要比内存访问更快速的，所以理论上讲，布隆过滤器的判重方式，更加快速。

总结引申

布隆过滤器非常适合这种不需要 100% 准确的、允许存在小概率误判的大规模判重场景。
除了爬虫网页去重这个例子，还有比如统计一个大型网站的每天的 UV 数，就可以使用布隆过滤器，对重复访问的用户，进行去重。
布隆过滤器的误判率，主要跟哈希函数的个数、位图的大小有关。当往布隆过滤器中不停地加入数据之后，位图中不是 true 的位置就越来越少了，误判率就越来越高了。所以，对于无法事先知道要判重的数据个数的情况，需要支持自动扩容的功能。当布隆过滤器中，数据个数与位图大小的比例超过某个阈值的时候，就重新申请一个新的位图。后面来的新数据，会被放置到新的位图中。
位图、布隆过滤器应用如此广泛，很多编程语言都已经实现了。比如 Java 中的 BitSet 类就是一个位图，Redis 也提供了 BitMap 位图类，Google 的 Guava 工具包提供了 BloomFilter 布隆过滤器的实现。