广度优先搜索（BFS）

广度优先搜索（Breadth-First-Search），会从指定的第一个顶点开始遍历图，先访问这个顶点的所有相邻顶点，然后再访问这些相邻顶点的相邻顶点：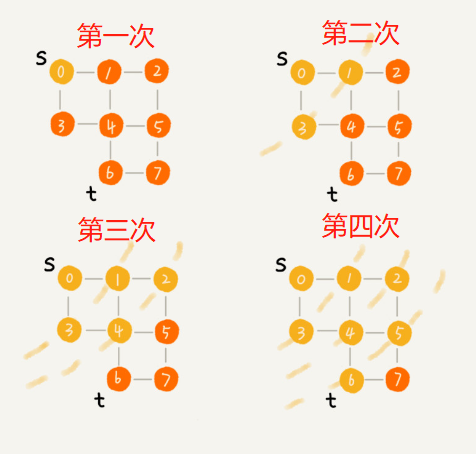
image.png
加权的图，广度优先算法并不是最合适的。

  1. let Colors = {
  2.   WHITE: 0, // 邻接顶点没有被访问过（颜色为白色）
  3.   GREY: 1, // 被访问过（颜色为灰色）
  4.   BLACK: 2 // 开始顶点（颜色为黑色）
  5. }
  7. let initializeColor = vertices => { 
  8.   let color = {}
  9.   vertices.forEach(v => color[v] = Colors.WHITE)
  10.   return color
  11. }
  13. let BFS = (graph, startVertex) => {
  14.   let vertices = graph.getVertices()
  15.   let adjList = graph.getAdjList()
  16.   let color = initializeColor(vertices) // 初始化所有的顶点标记为未被访问过（颜色为白色）
  17.   let queue = new Queue()
  18.   let distances = {} // 记录给定顶点到其它所有顶点的距离
  19.   let predecessors = {} // 记录所有顶点的前置顶点
  21.   queue.enqueue(startVertex)
  23.   // 初始化所有顶点的距离为0，前置节点为null
  24.   vertices.forEach(v => {
  25.     distances[v] = 0
  26.     predecessors[v] = null
  27.   })
  29.   while (!queue.isEmpty()) {
  30.     let current = queue.dequeue() // 队列先进先出
  31.     adjList.get(current).forEach(ele => {
  32.       if (color[ele] === Colors.WHITE) {
  33.         color[ele] = Colors.GREY
  34.         distances[ele] = distances[current] + 1
  35.         predecessors[ele] = current
  36.         queue.enqueue(ele)
  37.       }
  38.     })
  40.     color[current] = Colors.BLACK
  41.   }
  42.   return { distances, predecessors }
  43. }
  45. console.log(BFS(graph, 'A'))
  46. // {
  47. //   distances: { A: 0, B: 1, C: 1, D: 1, E: 2, F: 2, G: 2, H: 2, I: 3 },
  48. //   predecessors: {
  49. //     A: null,
  50. //     B: 'A',
  51. //     C: 'A',
  52. //     D: 'A',
  53. //     E: 'B',
  54. //     F: 'B',
  55. //     G: 'C',
  56. //     H: 'D',
  57. //     I: 'E'
  58. //   }
  59. // }
  61. // 求出从给定顶点A开始到其它所有顶点的最短路径
  62. let shortestPathA = BFS(graph, 'A')
  63. let startVertex = 'A'
  64. myVertices.forEach(v => {
  65.   let path = new Stack()
  66.   for (let v2 = v; v2 !== startVertex; v2 = shortestPathA.predecessors[v2]) {
  67.     path.push(v2)
  68.   }
  70.   path.push(startVertex)
  71.   let s = path.pop()
  72.   while (!path.isEmpty()) {
  73.     s += ` - ${path.pop()}`
  74.   }
  76.   console.log(s)
  77. })
  78. // A
  79. // A - B
  80. // A - C
  81. // A - D
  82. // A - B - E
  83. // A - B - F
  84. // A - C - G
  85. // A - D - H
  86. // A - B - E - I
  1. const INF = Number.MAX_SAFE_INTEGER
  2. const minDistance = (dist, visited) => {
  3.   let min = INF
  4.   let minIndex = -1
  5.   for (let v = 0; v < dist.length; v++) {
  6.     if (visited[v] === false && dist[v] <= min) {
  7.       min = dist[v]
  8.       minIndex = v
  9.     }
  10.   }
  11.   return minIndex
  12. }
  13. const dijkstra = (graph, src) => {
  14.   const dist = []
  15.   const visited = []
  16.   const { length } = graph
  17.   for (let i = 0; i < length; i++) {
  18.     dist[i] = INF
  19.     visited[i] = false
  20.   }
  21.   dist[src] = 0
  22.   for (let i = 0; i < length - 1; i++) {
  23.     const u = minDistance(dist, visited)
  24.     visited[u] = true
  25.     for (let v = 0; v < length; v++) {
  26.       if (!visited[v] && graph[u][v] !== 0 && dist[u] !== INF && dist[u] + graph[u][v] < dist[v]) {
  27.         dist[v] = dist[u] + graph[u][v]
  28.       }
  29.     }
  30.   }
  31.   return dist
  32. }
  1. const floydWarshall = graph => {
  2.   const dist = []
  3.   const { length } = graph
  4.   for (let i = 0; i < length; i++) {
  5.     dist[i] = []
  6.     for (let j = 0; j < length; j++) {
  7.       if (i === j) {
  8.         dist[i][j] = 0
  9.       } else if (!isFinite(graph[i][j])) {
  10.         dist[i][j] = Infinity
  11.       } else {
  12.         dist[i][j] = graph[i][j]
  13.       }
  14.     }
  15.   }
  16.   for (let k = 0; k < length; k++) {
  17.     for (let i = 0; i < length; i++) {
  18.       for (let j = 0; j < length; j++) {
  19.         if (dist[i][k] + dist[k][j] < dist[i][j]) {
  20.           dist[i][j] = dist[i][k] + dist[k][j]
  21.         }
  22.       }
  23.     }
  24.   }
  25.   return dist
  26. }
  1. const INF = Number.MAX_SAFE_INTEGER
  2. const find = (i, parent) => {
  3.   while (parent[i]) {
  4.     i = parent[i] // eslint-disable-line prefer-destructuring
  5.   }
  6.   return i
  7. }
  8. const union = (i, j, parent) => {
  9.   if (i !== j) {
  10.     parent[j] = i
  11.     return true
  12.   }
  13.   return false
  14. }
  15. const initializeCost = graph => {
  16.   const cost = []
  17.   const { length } = graph
  18.   for (let i = 0; i < length; i++) {
  19.     cost[i] = []
  20.     for (let j = 0; j < length; j++) {
  21.       if (graph[i][j] === 0) {
  22.         cost[i][j] = INF
  23.       } else {
  24.         cost[i][j] = graph[i][j]
  25.       }
  26.     }
  27.   }
  28.   return cost
  29. }
  30. const kruskal = graph => {
  31.   const { length } = graph
  32.   const parent = []
  33.   let ne = 0
  34.   let a
  35.   let b
  36.   let u
  37.   let v
  38.   const cost = initializeCost(graph)
  39.   while (ne < length - 1) {
  40.     for (let i = 0, min = INF; i < length; i++) {
  41.       for (let j = 0; j < length; j++) {
  42.         if (cost[i][j] < min) {
  43.           min = cost[i][j]
  44.           a = u = i
  45.           b = v = j
  46.         }
  47.       }
  48.     }
  49.     u = find(u, parent)
  50.     v = find(v, parent)
  51.     if (union(u, v, parent)) {
  52.       ne++
  53.     }
  54.     cost[a][b] = cost[b][a] = INF
  55.   }
  56.   return parent
  57. }
const INF = Number.MAX_SAFE_INTEGER
const minKey = (graph, key, visited) => {
  // Initialize min value
  let min = INF
  let minIndex = 0
  for (let v = 0; v < graph.length; v++) {
    if (visited[v] === false && key[v] < min) {
      min = key[v]
      minIndex = v
    }
  }
  return minIndex
}
const prim = graph => {
  const parent = []
  const key = []
  const visited = []
  const { length } = graph
  for (let i = 0; i < length; i++) {
    key[i] = INF
    visited[i] = false
  }
  key[0] = 0
  parent[0] = -1
  for (let i = 0; i < length - 1; i++) {
    const u = minKey(graph, key, visited)
    visited[u] = true
    for (let v = 0; v < length; v++) {
      if (graph[u][v] && !visited[v] && graph[u][v] < key[v]) {
        parent[v] = u
        key[v] = graph[u][v]
      }
    }
  }
  return parent
}

深度优先搜索（DFS）

深度优先搜索（Depth-First-Search），从图的第一个顶点开始，沿着这个顶点的一条路径递归查找到最后一个顶点，然后返回并探查路径上的其它路径，直到所有路径都被访问到。最终，深度优先算法会先深后广地访问图中的所有顶点。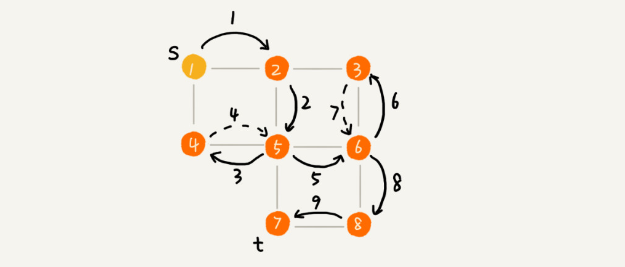
image.png

const Colors = {
  WHITE: 0,
  GREY: 1,
  BLACK: 2
}

const initializeColor = vertices => {
  let color = {}
  vertices.forEach(v => color[v] = Colors.WHITE)
  return color
}

const depthFirstSearch = (graph, callback) => {
  let vertices = graph.getVertices()
  let adjList = graph.getAdjList()
  let color = initializeColor(vertices) // 初始化将图中所有顶点的颜色初始化为白色。

  vertices.forEach(v => { // 挨个遍历
    if (color[v] === Colors.WHITE) {
      depthFirstSearchVisit(v, color, adjList, callback)
    }
  })
}

const depthFirstSearchVisit = (u, color, adjList, callback) => {
  color[u] = Colors.GREY // 进来访问就置灰
  if (callback) callback(u)

  adjList.get(u).forEach(n => { // 递归遍历相邻节点
    if (color[n] === Colors.WHITE) {
      depthFirstSearchVisit(n, color, adjList, callback)
    }
  })

  color[u] = Colors.BLACK // 最后没有邻接节点就设置为黑色
}
depthFirstSearch(graph, value => console.log(`visited vertex: ${value}`));
// visited vertex: A
// visited vertex: B
// visited vertex: E
// visited vertex: I
// visited vertex: F
// visited vertex: C
// visited vertex: D
// visited vertex: G
// visited vertex: H

let DFSVisit = (u, color, discovery, finished, predecessors, time, adjList) => {
  color[u] = Colors.GREY
  discovery[u] = ++time.count

  adjList.get(u).forEach(n => {
    if (color[n] === Colors.WHITE) {
      predecessors[n] = u
      DFSVisit(n, color, discovery, finished, predecessors, time, adjList)
    }
  })

  color[u] = Colors.BLACK
  finished[u] = ++time.count
}

let DFS = graph => {
  let vertices = graph.getVertices()
  let adjList = graph.getAdjList()
  let color = initializeColor(vertices)
  let discovery = {}  // 保存每个顶点的发现时间
  let finished = {} // 保存每个顶点探索时间
  let predecessors = {} // 保存每个顶点的前置顶点
  let time = { count: 0 } // 假定时间从0开始，每经过一步时间值加1

  vertices.forEach(v => {
    finished[v] = 0
    discovery[v] = 0
    predecessors[v] = null
  })

  vertices.forEach(v => {
    if (color[v] === Colors.WHITE) {
      DFSVisit(v, color, discovery, finished, predecessors, time, adjList)
    }
  })

  return { discovery, finished, predecessors }
}
console.log(DFS(graph))
// {
//   discovery: { A: 1, B: 2, C: 10, D: 11, E: 3, F: 7, G: 12, H: 14, I: 4 },
//   finished: { A: 18, B: 9, C: 17, D: 16, E: 6, F: 8, G: 13, H: 15, I: 5 },
//   predecessors: {
//     A: null,
//     B: 'A',
//     C: 'A',
//     D: 'C',
//     E: 'B',
//     F: 'B',
//     G: 'D',
//     H: 'D',
//     I: 'E'
//   }
// }